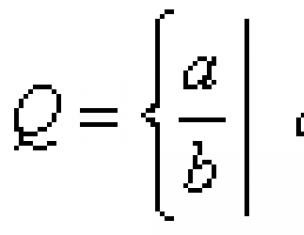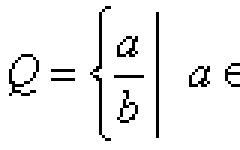С отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .
Иррациональными являются:
Примеры доказательства иррациональности
Корень из 2
Допустим противное: рационален , то есть представляется в виде несократимой дроби , где и - целые числа . Возведём предполагаемое равенство в квадрат:
.Отсюда следует, что чётно, значит, чётно и . Пускай , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и - иррациональное число.
Двоичный логарифм числа 3
Допустим противное: рационален , то есть представляется в виде дроби , где и - целые числа . Поскольку , и могут быть выбраны положительными. Тогда
Но чётно, а нечётно. Получаем противоречие.
e
История
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. - ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу , который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:
- Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a :b , где a и b выбраны наименьшими из возможных.
- По теореме Пифагора: a ² = 2b ².
- Так как a ² четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
- Поскольку a :b несократима, b обязано быть нечетным.
- Так как a четное, обозначим a = 2y .
- Тогда a ² = 4y ² = 2b ².
- b ² = 2y ², следовательно b ² четное, тогда и b четно.
- Однако было доказано, что b нечетное. Противоречие.
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
См. также
Примечания
| Числовые системы | |
|---|---|
| Счётные множества |
Натуральные числа () |
Множество иррациональных чисел обычно обозначается заглавной латинской буквой I {\displaystyle \mathbb {I} } в полужирном начертании без заливки. Таким образом: I = R ∖ Q {\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} } , то есть множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.
О существовании иррациональных чисел, точнее отрезков , несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .
Энциклопедичный YouTube
-
1 / 5
Иррациональными являются:
Примеры доказательства иррациональности
Корень из 2
Допустим противное: 2 {\displaystyle {\sqrt {2}}} рационален , то есть представляется в виде дроби m n {\displaystyle {\frac {m}{n}}} , где m {\displaystyle m} - целое число , а n {\displaystyle n} - натуральное число .
Возведём предполагаемое равенство в квадрат:
2 = m n ⇒ 2 = m 2 n 2 ⇒ m 2 = 2 n 2 {\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}} .История
Античность
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. - ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены [ ] .
Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу . Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок [ ] .
Нет точных данных о том, иррациональность какого числа было доказано Гиппасом. Согласно легенде он нашёл его изучая длины сторон пентаграммы. Поэтому разумно предположить, что это было золотое сечение [ ] .
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
Понимание чисел, особенно натуральных чисел, является одним из старейших математических "умений". Многие цивилизации, даже современные, приписывали числам некие мистические свойства ввиду их огромной важности в описании природы. Хотя современная наука и математика не подтверждают эти "волшебные" свойства, значение теории чисел неоспоримо.
Исторически сначала появилось множество натуральных чисел, затем довольно скоро к ним добавились дроби и положительные иррациональные числа. Ноль и отрицательные числа были введены после этих подмножеств множества действительных чисел. Последнее множество, множество комплексных чисел, появилось только с развитием современной науки.
В современной математике числа вводят не в историческом порядке, хотя и в довольно близком к нему.
Натуральные числа $\mathbb{N}$
Множество натуральных чисел часто обозначается как $\mathbb{N}=\lbrace 1,2,3,4... \rbrace $, и часто его дополняют нулем, обозначая $\mathbb{N}_0$.
В $\mathbb{N}$ определены операции сложения (+) и умножения ($\cdot$) со следующими свойствами для любых $a,b,c\in \mathbb{N}$:
1. $a+b\in \mathbb{N}$, $a\cdot b \in \mathbb{N}$ множество $\mathbb{N}$ замкнуто относительно операций сложения и умножения
2. $a+b=b+a$, $a\cdot b=b\cdot a$ коммутативность
3. $(a+b)+c=a+(b+c)$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$ ассоциативность
4. $a\cdot (b+c)=a\cdot b+a\cdot c$ дистрибутивность
5. $a\cdot 1=a$ является нейтральным элементом для умноженияПоскольку множество $\mathbb{N}$ содержит нейтральный элемент для умножения, но не для сложения, добавление нуля к этому множеству обеспечивает включение в него нейтрального элемента для сложения.
Кроме этих двух операций, на множестве $\mathbb{N}$ определены отношения "меньше" ($
1. $a b$ трихотомия
2. если $a\leq b$ и $b\leq a$, то $a=b$ антисимметрия
3. если $a\leq b$ и $b\leq c$, то $a\leq c$ транзитивность
4. если $a\leq b$, то $a+c\leq b+c$
5. если $a\leq b$, то $a\cdot c\leq b\cdot c$Целые числа $\mathbb{Z}$
Примеры целых чисел:
$1, -20, -100, 30, -40, 120...$Решение уравнения $a+x=b$, где $a$ и $b$ - известные натуральные числа, а $x$ - неизвестное натуральное число, требует введения новой операции - вычитания(-). Если существует натуральное число $x$, удовлетворяющее этому уравнению, то $x=b-a$. Однако, это конкретное уравнение не обязательно имеет решение на множестве $\mathbb{N}$, поэтому практические соображения требуют расширения множества натуральных чисел таким образом, чтобы включить решения такого уравнения. Это приводит к введению множества целых чисел: $\mathbb{Z}=\lbrace 0,1,-1,2,-2,3,-3...\rbrace$.
Поскольку $\mathbb{N}\subset \mathbb{Z}$, логично предположить, что введенные ранее операции $+$ и $\cdot$ и отношения $ 1. $0+a=a+0=a$ существует нейтральный элемент для сложения
2. $a+(-a)=(-a)+a=0$ существует противоположное число $-a$ для $a$Свойство 5.:
5. если $0\leq a$ и $0\leq b$, то $0\leq a\cdot b$Множество $\mathbb{Z} $ замкнуто также и относительно операции вычитания, то есть $(\forall a,b\in \mathbb{Z})(a-b\in \mathbb{Z})$.
Рациональные числа $\mathbb{Q}$
Примеры рациональных чисел:
$\frac{1}{2}, \frac{4}{7}, -\frac{5}{8}, \frac{10}{20}...$Теперь рассмотрим уравнения вида $a\cdot x=b$, где $a$ и $b$ - известные целые числа, а $x$ - неизвестное. Чтобы решение было возможным, необходимо ввести операцию деления ($:$), и решение приобретает вид $x=b:a$, то есть $x=\frac{b}{a}$. Опять возникает проблема, что $x$ не всегда принадлежит $\mathbb{Z}$, поэтому множество целых чисел необходимо расширить. Таким образом вводится множество рациональных чисел $\mathbb{Q}$ с элементами $\frac{p}{q}$, где $p\in \mathbb{Z}$ и $q\in \mathbb{N}$. Множество $\mathbb{Z}$ является подмножеством, в котором каждый элемент $q=1$, следовательно $\mathbb{Z}\subset \mathbb{Q}$ и операции сложения и умножения распространяются и на это множество по следующим правилам, которые сохраняют все вышеперечисленные свойства и на множестве $\mathbb{Q}$:
$\frac{p_1}{q_1}+\frac{p_2}{q_2}=\frac{p_1\cdot q_2+p_2\cdot q_1}{q_1\cdot q_2}$
$\frac{p-1}{q_1}\cdot \frac{p_2}{q_2}=\frac{p_1\cdot p_2}{q_1\cdot q_2}$Деление вводится таким образом:
$\frac{p_1}{q_1}:\frac{p_2}{q_2}=\frac{p_1}{q_1}\cdot \frac{q_2}{p_2}$На множестве $\mathbb{Q}$ уравнение $a\cdot x=b$ имеет единственное решение для каждого $a\neq 0$ (деление на ноль не определено). Это значит, что существует обратный элемент $\frac{1}{a}$ or $a^{-1}$:
$(\forall a\in \mathbb{Q}\setminus\lbrace 0\rbrace)(\exists \frac{1}{a})(a\cdot \frac{1}{a}=\frac{1}{a}\cdot a=a)$Порядок множества $\mathbb{Q}$ можно расширить таким образом:
$\frac{p_1}{q_1}Множество $\mathbb{Q}$ имеет одно важное свойство: между любыми двумя рациональными числами находится бесконечно много других рациональных чисел, следовательно, не существует двух соседних рациональных чисел, в отличие от множеств натуральных и целых чисел.
Иррациональные числа $\mathbb{I}$
Примеры иррациональных чисел:
$\sqrt{2} \approx 1.41422135...$
$\pi \approx 3.1415926535...$Ввиду того, что между любыми двумя рациональными числами находится бесконечно много других рациональных чисел, легко можно сделать ошибочный вывод, что множество рациональных чисел настолько плотное, что нет необходимости в его дальнейшем расширении. Даже Пифагор в свое время сделал такую ошибку. Однако, уже его современники опровергли этот вывод при исследовании решений уравнения $x\cdot x=2$ ($x^2=2$) на множестве рациональных чисел. Для решения такого уравнения необходимо ввести понятие квадратного корня, и тогда решение этого уравнения имеет вид $x=\sqrt{2}$. Уравнение типа $x^2=a$, где $a$ - известное рациональное число, а $x$ - неизвестное, не всегда имеет решение на множестве рациональных чисел, и опять возникает необходимость в расширении множества. Возникает множество иррациональных чисел, и такие числа как $\sqrt{2}$, $\sqrt{3}$, $\pi$... принадлежат этому множеству.
Действительные числа $\mathbb{R}$
Объединением множеств рациональных и иррациональных чисел является множество действительных чисел. Поскольку $\mathbb{Q}\subset \mathbb{R}$, снова логично предположить, что введенные арифметические операции и отношения сохраняют свои свойства на новом множестве. Формальное доказательство этого весьма сложно, поэтому вышеупомянутые свойства арифметических операций и отношения на множестве действительных чисел вводятся как аксиомы. В алгебре такой объект называется полем, поэтому говорят, что множество действительных чисел является упорядоченным полем.
Для того, чтобы определение множества действительных чисел было полным, необходимо ввести дополнительную аксиому, различающую множества $\mathbb{Q}$ и $\mathbb{R}$. Предположим, что $S$ - непустое подмножество множества действительных чисел. Элемент $b\in \mathbb{R}$ называется верхней границей множества $S$, если $\forall x\in S$ справедливо $x\leq b$. Тогда говорят, что множество $S$ ограничено сверху. Наименьшая верхняя граница множества $S$ называется супремум и обозначается $\sup S$. Аналогично вводятся понятия нижней границы, множества, ограниченного снизу, и инфинума $\inf S$ . Теперь недостающая аксиома формулируется следующим образом:
Любое непустое и ограниченное сверху подмножество множества действительных чисел имеет супремум.
Также можно доказать, что поле действительных чисел, определенное вышеуказанным образом, является единственным.Комплексные числа$\mathbb{C}$
Примеры комплексных чисел:
$(1, 2), (4, 5), (-9, 7), (-3, -20), (5, 19),...$
$1 + 5i, 2 - 4i, -7 + 6i...$ где $i = \sqrt{-1}$ или $i^2 = -1$Множество комплексных чисел представляет собой все упорядоченные пары действительных чисел, то есть $\mathbb{C}=\mathbb{R}^2=\mathbb{R}\times \mathbb{R}$, на котором операции сложения и умножения определены следующим образом:
$(a,b)+(c,d)=(a+b,c+d)$
$(a,b)\cdot (c,d)=(ac-bd,ad+bc)$Существует несколько форм записи комплексных чисел, из которых самая распространенная имеет вид $z=a+ib$, где $(a,b)$ - пара действительных чисел, а число $i=(0,1)$ называется мнимой единицей.
Легко показать, что $i^2=-1$. Расширение множества $\mathbb{R}$ на множество $\mathbb{C}$ позволяет определить квадратный корень из отрицательных чисел, что и послужило причиной введения множества комплексных чисел. Также легко показать, что подмножество множества $\mathbb{C}$, заданное как $\mathbb{C}_0=\lbrace (a,0)|a\in \mathbb{R}\rbrace$, удовлетворяет всем аксиомам для действительных чисел, следовательно $\mathbb{C}_0=\mathbb{R}$, или $R\subset\mathbb{C}$.
Алгебраическая структура множества $\mathbb{C}$ относительно операций сложения и умножения имеет следующие свойства:
1. коммутативность сложения и умножения
2. ассоциативность сложения и умножения
3. $0+i0$ - нейтральный элемент для сложения
4. $1+i0$ - нейтральный элемент для умножения
5. умножение дистрибутивно по отношению к сложению
6. существует единственный обратный элемент как для сложения, так и для умножения.Дробь m/n будем считать несократимой (ведь сократимую дробь всегда можно привести к несократимому виду). Возведя обе части равенства в квадрат, получим m ^2=2n ^2. Отсюда заключаем, что m^2, а следом за этим и число m - чётное. т.е. m = 2k . Поэтому m ^2 = 4k ^2 и, следовательно, 4k ^2 =2n ^2, или 2k ^2 = n ^2. Но тогда получается, что и n также чётное число, а этого быть не может, поскольку дробь m/n несократима. Возникает противоречие. Остаётся сделать вывод: наше предположение неверно и рационального числа m/n , равного √2, не существует.»
Вот и всё их доказательство.
Критическая оценка доказательства древних греков
Но…. посмотрим на такое доказательство древних греков несколько критично. И если быть более аккуратным в простой математике, то в нём можно увидеть следующее:1) В принятом у греков рациональном числе m/n числа m и n – целые, но неизвестные (то ли они чётные , то ли они нечётные ). И это так! А чтобы как-то установить между ними какую-либо зависимость, надо точно определиться с их назначением;
2) Когда древние определились с тем, что число m – чётное, то в принятом ими равенстве m = 2k они (умышленно или по незнанию!) не совсем «корректно» охарактеризовали число «k ». А ведь здесь число k – это целое (ЦЕЛОЕ!) и вполне известное число, вполне чётко определяющее найденное чётное число m . И не будь этого найденного числа «k » древние не могли бы в дальнейшем «использовать » и число m ;
3) А когда из равенства 2k ^2 = n ^2 древние получили число n ^2 чётное, а вместе с тем и n – чётное, то им надо было бы не спешить с выводом о «возникшем противоречии », а лучше удостовериться в предельной точности принятого ими «выбора » числа «n ».
А как это можно было им сделать? Да, просто!
Смотрите: из полученного ими равенства 2k ^2 = n ^2 можно было элементарно получить и такое равенство k √2 = n . И здесь никак нет ничего предосудительного – ведь получили же они из равенства m/n =√2 другое адекватное ему равенство m ^2=2n ^2 ! И никто им не перечил!Но зато в новом равенстве k √2 = n при очевидных ЦЕЛЫХ числах k и n видно, что из него всегда получают число √2 - рациональное . Всегда! Поскольку в нём числа k и n - известные ЦЕЛЫЕ!
А вот чтобы из их равенства 2k ^2 = n ^2 и, как следствие этого, из k √2 = n получить число √2 – иррациональное (как того «пожелали » древние греки!), то в них необходимо иметь, как минимум , число «k » в виде нецелого (!!!) числа. А этого у древних греков как раз и НЕТ!
Отсюда и ВЫВОД: вышеприведённое доказательство иррациональности числа √2, сделанное древними греками 2400 лет тому назад, откровенно неверное и математически некорректно, если не сказать грубо – оно просто фальшивое .
В показанной выше небольшой брошюрке Ф-6 (см. фото выше), выпущенной в г. Краснодар (Россия) в 2015 году общим тиражом 15000 экз. (очевидно, со спонсорским вложением) приведено новое, предельно-корректное с точки зрения математики и предельно-верное ]доказательство иррациональности числа √2, которое давно могло бы состояться, не будь жёстких "препо н" к изучению древностей Истории.
1.Доказательство является примерами дедуктивного рассуждения и отличаются от индуктивных или эмпирических аргументов. Доказательство должно продемонстрировать, что доказываемое утверждение всегда верно, иногда путем перечисления всех возможных случаев и показывая, что утверждение выполняется в каждом из них. Доказательство может опираться на очевидные или общепринятые явления или случаи, известные как аксиомы. Вопреки этому, доказывается иррациональность “корня квадратного из двух”.
2.Вмешательство топологии здесь объясняется самой природой вещей, что означает, что чисто алгебраического способа доказательства иррациональности, в частности, исходя из рациональных чисел нет.Вот пример, за вами право выбора: 1+1/2 + 1/4 + 1/8 ….= 2 или 1+1/2 + 1/4 + 1/8 …≠ 2 ???
Если вы примете 1+1/2 + 1/4 + 1/8 +…= 2, что считается “алгебраическим” подходом, то совсем не составляет труда показать, что существует n/m ∈ ℚ, которое на бесконечной последовательности является иррациональным и конечным числом.Это подсказывает, что иррациональные числа являются замыканием поля ℚ, но это относится к топологической особенности.
Так для чисел Фибоначчи, F(k): 1,1,2,3,5,8,13,21,34,55,89,144,233,377, … lim{F(k+1)/F(k)} = φ
Это лишь показывает, что существует непрерывный гомоморфизм ℚ → I, и можно показать строго, что существования такого изоморфизма не является логическим следствием алгебраических аксиом.