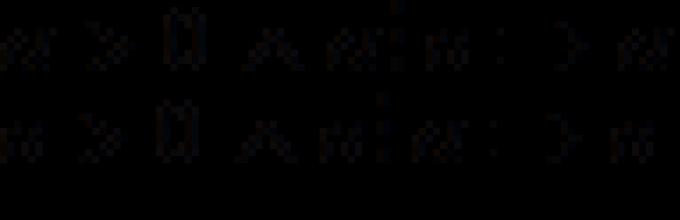Пусть даны натуральные числа a и b . Говорят, что число a делится на число b , если существует такое натуральное число q , что a = bq .
В этом случае число b называют делителем числа а , а число а - кратным числа b .
Например, 24 делится на 8, так как существует такое q = 3, что 24 = 8*3. Можно сказать иначе: 8 - это делитель числа 24, а 24 есть кратное числа 8.
В случае, когда а делится на b , пишут: . Эту запись часто читают и так: «а кратно b ».
Заметим, что понятие «делитель данного число» следует отличать от понятия «делитель», обозначающего то число, на которое делят. Например, если 18 делят на 5, то число 5 - делитель, но 5 не является делителем числа 18. Если 18 делят на 6, то в случае понятия «делитель» и «делитель данного числа» совпадают.
Из определения отношения делимости и равенства а = 1*а , справедливого для любого натурального а, вытекает, 1 является делителем любого натурального числа.
Выясним, сколько вообще делителем может быть у натурального числа. Сначала рассмотрим следующую теорему.
Теорема. Делитель b данного числа а не превышает этого числа. Если , то .
Доказательство. Так как , то существует такое , что a = bq , значит, a - b = bq - b = b*(q - 1). Поскольку , то . Тогда и, следовательно, .
Из данной теоремы следует, что множество делителей данного числа конечно. Назовем, например, все делители числа 36. Они образуют конечное множество {1, 2, 3, 4, 6, 9, 12, 18, 36}.
Свойства делимости
Нам известно, что отношение делимости на множестве N обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства.
Теорема. Отношение делимости рефлексивно, т.е. любое нату-ральное число делится само на себя.
Доказательство. Для любого натурального а справедливо ра-венство . Так как 1 е N, то, по определению отношения дели-мости, .
Теорема. Отношение делимости антисимметрично, т.е. если и , то .
Доказательство . Предположим противное, т. е. что . Но тог-да , согласно теореме, рассмотренной выше.
По условию и . Тогда, по той же теореме,.
Неравенства и будут справедливы лишь тогда, когда , что противоречит условию теоремы. Следовательно, наше предпо-ложение неверное и теорема доказана.
Теорема. Отношение делимости транзитивно, т.е. если и , то .
Доказательство. Так как, q, что а = bq, а так как , то существует такое натуральное число p , что . Но тогда имеем: . Число pq - натуральное. Значит, по определению отношения делимости,.
Теорема (признак делимости суммы). Если каждое из натураль-ных чисел а1 , а2 ..., ап делится на натуральное число b , то и их сумма а1 + а2 + ... + ап делится на это число.
Доказательство . Так как , то существует такое натураль-ное число что . Так как , то существует такое нату-ральное число , что . Продолжая рассуждения, получим, что если , то существует такое натуральное число , что . Эти равенства позволяют преобразовать сумму а1 + а2 + ... + ап в сумму вида bq1 + bq2 + ... + bqn. Вынесем за скобки общий множитель b, а получившееся в скобках натуральное число q1 + q2 + ... + qn обозначим буквой q . Тогда а1 + а2 + ... + ап = b(q1 + q2 + ... + qn) = bq , т.е. сумма а1 + а2 + ... + ап оказалась представленной в виде произведения числа b и некоторого натурального числа q. А это значит, что сумма а1 + а2 + ... + ап делится на b, что и требовалось доказать.
Например, не производя вычислений, можно сказать, что сумма 175 + 360 + 915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.
Теорема (признак делимости разности). Если числа а1 и а2 делятся на b и , то их разность делится на b.
Доказательство этой теоремы аналогично доказательству призна-ка делимости суммы.
Теорема (признак делимости произведения). Если число а де-лится на b, то произведение вида ах, где xÎ N, делится на b.
Доказательство . Так как , то существует такое натураль-ное число q, что . Умножим обе части этого равенства на нату-ральное число х. Тогда ах = (bq)x, откуда на основании свойства ассоциативности умножения (bq)x = b(qx) и, значит, ах = b(qx), где qx - натуральное число. Согласно определению отношения делимости, , что и требовалось доказать.
Из доказанной теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b.
Например, произведение 24
Определение. Пусть даны натуральные числа а и b. Говорят, что число а делится на число b, если существует такое натуральное число q, что а = bq.
В этом случае число b называютделителем числа а , а число а - кратным числа b.
Например , 24 делится на 8, так как существует такое q = 3, что 24 = 8×3. Можно сказать иначе: 8 - это делитель числа 24, а 24 есть кратное числа 8.
В том случае, когда а делится на b, пишут: а M b. Эту запись часто читают и так: «а кратно b».
Заметим, что понятие «делитель данного числа» следует отличать от понятия «делитель», обозначающего то число, на которое делят. Например, если 18 делят на 5, то число 5 - делитель, но 5 не является делителем числа 18. Если 18 делят на 6, то в этом случае понятия «делитель» и «делитель данного числа» совпадают.
Из определения отношения делимости и равенства a = 1 × а, справедливого для любого натурального а, вытекает, что 1 является делителем любого натурального числа.
Выясним, сколько вообще делителей может быть у натурального числа а. Сначала рассмотрим следующую теорему.
Теорема 1. Делитель b данного числа а не превышает этого числа, т. е. если а M b, то b £ а.
Доказательство. Так как а M b, то существует такое qÎ N, что а = bq и, значит, а - b = bq - b = b ×(q - 1). Поскольку qÎ N, то q ³ 1. . Тогда b ×(q - 1) ³ 0 и, следовательно, и b £ а.
Из данной теоремы следует, что множество делителей данного числа конечно. Назовем, например, все делители числа 36. Они образуют конечное множество {1,2,3,4,6,9, 12, 18,36}.
В зависимости от числа делителей среди натуральных чисел различают простые и составные числа.
Определение. Простым числом называется такое натуральное число, большее 1, которое имеет только два делителя - единицу и само это число.
Например , 13 – простое, поскольку у него только два делителя: 1 и 13.
Определение. Составным числом называется такое натуральное число, которое имеет более двух делителей.
Так число 4 составное, у него три делителя: 1, 2 и 4. Число 1 не является ни простым, ни составным числом в связи с тем, что оно имеет только один делитель.
Чисел, кратных данному числу, можно назвать как угодно много, -их бесконечное множество. Так, числа, кратные 4, образуют бесконечный ряд: 4, 8, 12, 16, 20, 24, .... и все они могут быть получены по формуле а = 4q, где q принимает значения 1, 2, 3,... .
Нам известно, что отношение делимости на множестве N обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства.
Теорема 2. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя.
Доказательство. Для любого натурального а справедливо равенство а = а× 1. Так как 1 Î N то, по определению отношения делимости, аMа.
Теорема 3 . Отношение делимости антисимметрично, т.е. если а M b и а ¹ b, то .
Доказательство. Предположим противное, т. е. что bMа. Но тогда а£ b, согласно теореме, рассмотренной выше.
По условию а M b и а ¹ b. Тогда, по той же теореме, b £ а.
Неравенства а £ b и b £ а.будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и теорема доказана.
Теорема 4. Отношение делимости транзитивно, т.е. если а M b и b M с, то а M с.
Доказательство. Так как а M b, q, что а = b q , а так как bM с, то существует такое натуральное число р , что b = ср. Но тогда имеем: а = b q = (ср)q = с(рq). Число рq - натуральное. Значит, по определению отношения делимости, а. M с.
Теорема 5 (признак делимости суммы). Если каждое из натуральных чисел а 1, а 2 ,…а п делится на натуральное число b, то и их сумма а 1 + а 2 + … + а п делится на это число.
Например , не производя вычислений, можно сказать, что сумма 175 + 360 +915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.
Теорема 6 (признак делимости разности). Если числа а 1 и а 2 делятся на b и а 1 ³ а 2 , то их разность а 1 - а 2 делится на b.
Теорема 7 (признак делимости произведения). Если число а делится на b, то произведение вида ах, где х е N. делится на b.
Из теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b.
Например , произведение 24×976×305 делится на 12, так как на 12 делится множитель 24.
Рассмотрим еще три теоремы, связанные с делимостью суммы и произведения, которые часто используются при решении задач на делимость.
Теорема 8. Если в сумме одно слагаемое не делится на число b, а все остальные слагаемые делятся на число b, то вся сумма на число b не делится.
Например, сумма 34 + 125 + 376 + 1024 на 2 не делится, так как 34:2,376: 2,124: 2,но 125 не делится на 2.
Теорема 9. Если в произведении аb множитель а делится на натуральное число т, а множитель b делится на натуральное число п то а b делится на тп.
Справедливость этого утверждения вытекает из теоремы о делимости произведения.
Теорема 10. Если произведение ас делится на произведение bс, причем с - натуральное число, то и а делится на b.
Определение. Говорят, что число а делится на число в, если существует такое число c Î N 0 , что а = в · с.
В том случае, когда а делится на в пишут: а в. Читают: «а делится на в »; «а кратно в »; «в – делитель а ». Например, 12 делится на 6, так как существует такое с = 2, что 12 = 6 · 2, иначе 12 6.
Замечание . Записи и а : в не равносильны. Первое обозначает, что между числами а и в имеет место отношение делимости (возможно нацело число а разделить на число в ). Второе – есть обозначение частного чисел а и в .
Отношение делимости обладает рядом свойств.
1°. Нуль делится на любое натуральное число, т.е.
(" в Î N ) .
Доказательство. 0 = в · 0для любого в, отсюда по определению следует, что 0 в .
2°. Ни одно натуральное число не делится на нуль, т.е. ("а Î N ) [а 0].
Доказательство (от противного). Пусть существует c Î N 0 , такое, что а = 0· с, но по условию а ≠ 0,значит ни при каком с это равенство не выполняется. Значит, наше предположение о существовании с было неверным и а 0.
3°. Любое целое неотрицательное число делится на единицу, т.е.
("а Î N ) [а 1].
Доказательство. а = 1· а => а 1.
4°. Любое натуральное число делится само на себя (рефлексивность), т.е.("а Î N ) [а а ].
Доказательство. а = а · 1Þ а а.
5°. Делитель в данного натурального числа а не превышает этого числа, т.е. (а в Ù а > 0) Þ (а ≥ в ).
Доказательство. Так как а в, то а = в · с, где c Î N 0 . Определим знак разности а – в.
а – в = вс – в = в (с – 1),поскольку а > 0, то с ≥ 1, следовательно, в (с – 1) ≥ 0,значит а – в ≥ 0 Þ а ≥ в .
6°. Отношение делимости антисимметрично, т.е.
("a, в ÎN 0 )[(a в Ùв а ) Þ а = в ].
Доказательство.
1 случай. Пусть а > 0, в > 0,тогда имеем:
![]() (по свойству 5°). Значит, а
= в
.
(по свойству 5°). Значит, а
= в
.
2 случай. Пусть хотя бы одно из чисел а или в равно 0.
Пусть а = 0, то в = 0по 2°, т.к. иначе в не могло бы делиться на а. Значит а = в.
7°. Отношение делимости транзитивно, т.е.
(" a, в, с Î N 0 ) [(a в Ù в с )Þ а с ].
Доказательство. а в Þ ($к )[а = вк ]; в с Þ ($ℓ )[в = cℓ ].
а = вк = (сℓ )к = с (ℓк ), ℓк – произведение двух неотрицательных целых чисел ℓ и к и потому само является целым неотрицательным, т.е. а с.
8°. Если каждое из чисел а и в делится на с, то их сумма а + в делится на с, т.е. ("a, в, с Î N 0 ) [(a с Ù в с ) Þ (а + в ) с ].
Доказательство, а с Þ а = ск, в с Þ в = cℓ.
а + в = ск + cℓ = с (к + ℓ ), т.к. к + ℓ –целое неотрицательное число, значит (а + в ) с.
Доказанное утверждение справедливо и в случае, когда число слагаемых больше двух.
Если каждое из чисел а 1 , ..., а п делится на с, то их сумма а 1 + ... + а п делится на с.
Кроме того, если числа а и в делятся на с, причем а ≥ в , то их разность а – в делится на с.
9°. Если число а делится на с , то произведение вида ах, где x ÎN 0 , делится на с, т.е. а с Þ (" x Î N 0 )[ax с ].
Доказательство. а с Þ а = ск, но тогда ах = скх = с (к · х ), к, x Î N 0 , значит ах с.
Следствие из 8°, 9°.
Если каждое из чисел а 1 , а 2 , ..., а п делится на с, то каковы бы ни были числа х 1 , х 2 , ... , х n число а 1 х 1 + а 2 х 2 + ... + а n х n делится на с.
10°. Если ас делится на вс, причем с ≠ 0, то а делится на в, т.е. (ас вс Ù с ≠ 0) Þ а в.
Доказательство.
ас = вс · к; ас = (вк ) · с Ù с ≠ 0 Þ а = вк => а в .
Признаки делимости
Встречаются задачи, в которых, не производя деления, требуется установить делится или нет натуральное число а на натуральное число в. Чаще всего такие задачи возникают, когда число а надо разложить на множители. В подобных задачах пользуются признаками делимости. Признак делимости – это предложение, позволяющее ответить на вопрос, делится или нет некоторое число на данный делитель, не производя самого деления.
Применяя признак делимости, делить все-таки приходится, конечно. Из школы хорошо известен признак делимости числа на 3. Делится ли число 531246897 на 3? Для ответа на вопрос определим сумму цифр этого числа 5 + 3 + 1 + 2 + 4 + 6 + 8 + 9 + 7 = 45, т.к. 45 делится на 3, то данное число делится на 3.
Итак, вопрос о делимости данного натурального числа сведен к вопросу о делимости меньшего натурального числа.
Признаки делимости зависят от системы счисления. Рассмотрим некоторые признаки делимости в десятичной системе счисления.
ДЕЛИМОСТЬ ЧИСЕЛ. ПРИЗНАКИ ДЕЛИМОСТИ
Рассмотрим отношение делимости в кольце целых чисел. Говорят, что число a
делится на b
, существует такое целое число q
, для которого a = qb.
Для отношения делимости справедливы следующие свойства.
Свойство 1.
Если a
делится на b
и b
делится на c
, то a
делится на c.
Свойство 2.
Если a
1, … , a
n
делятся на b
, то и a
1 + … + a
n
делится на b.
Свойство 3.
Если a
1 делится на b
1, … , a
n
делится на b
n
, то и a
1…a
n
делится на b
1…b
n
.
Имеет место следующая теорема о делении с остатком.
Теорема.
Для произвольных целого числа a
и натурального числа b
существуют единственные числа q
и r
такие, что a = qb + r
и 0 r < b
. Число q
называется неполным частным, а число r
– остатком.
Приведем два доказательства этой теоремы. Первое из книги .
Доказательство 1.
Пусть сначала a 0. Будем выписывать одно за другим числа a, a – b, a -
2b, …
до тех пор, пока не появится отрицательное число. Пусть последним из неотрицательных членов этой последовательности будет число a – qb.
Обозначая его через r,
мы имеем a = qb + r.
Очевидно, что r < b
(иначе число r – b = a –
(q +
1)b
было бы неотрицательным).
Пусть теперь a <
0. Рассуждая аналогично предыдущему, будем выписывать поледовательность чисел a, a + b, a +
2b, …
до тех пор, пока не появится первое неотрицательное число r
(легко проверить, что r < b
). Пусть r
=
a
+
q
"
b
.
Тогда, обозначая –q"
через q
, получаем a = qb + r.
Что и требовалось доказать.
Докажем единственность, т. е., что из a = qb + r
и a = q"b + r"
следует q = q"
и r = r"
. В этом случае имеем равенство qb + r = q"b + r"
, откуда r – r" =
(q" – q
)b,
т. е. r – r"
делится на b
. Но |r – r"
| < b
, и равенство r – r" =
(q" – q
)b
возможно только в случае r – r" =
0.
Но тогда (q" – q
)b
= 0 и, следовательно, q" – q =
0.
Приведем другое доказательство с геометрической интерпретацией.
Доказательство 2.
Заметим, что система промежутков [qb
, (q
+ 1)b
), где q
– целое, покрывает все множество целых чисел. Число a
попадает в один и только один из этих промежутков, т. е. существует единственное q
, для которого qb
a < qb + b.
Обозначим r = a – qb.
Тогда будем иметь: a = qb + r
и 0 r < b
.
Теорему о делении с остатком можно использовать для нахождения наибольшего общего делителя НОД(a
, b
) двух натуральных чисел a
и b
.
Напомним, что наибольшим общим делителем двух натуральных чисел a и b называется наибольшее из чисел, являющихся делителями a и b одновременно. Докажем, что такое число существует. Действительно, если c является делителем натурального числа a , то |c | a . Следовательно, у каждого натурального числа имеется конечное число делителей. Таким образом, число общих делителей двух натуральных чисел конечно и, значит, среди них есть наибольший элемент – наибольший общий делитель.
Заметим, что из равенства a
= qb
+ r
, где 0 r
< b
, следует, что каждый делитель чисел a
и b
является делителем чисел b
и r
и наоборот. Следовательно, НОД(a
, b
) = НОД(b
, r
). Если r
отлично от нуля, то разделим b
на r
с остатком. Получим b
= q
1r
+ r
1, где 0 r
1 < r
, и НОД(b
, r
) = НОД(r
, r
1). Продолжая этот процесс деления, придем к ситуации, когда r
k
+1 = 0, т. е. r
k
– 1 делится на r
k
и, значит, НОД(a
, b
) = НОД(b
, r
) = НОД(r
, r
1) = … = НОД(r
k
-1, r
k
) = r
k
.
Этот метод нахождения наибольшего общего делителя содержится в "Началах" Евклида и называется алгоритмом Евклида.
Пример.
Найти наибольший общий делитель чисел 168 и 70.
Имеем, 168 = 270 + 28, 70 = 228 + 14, 28 = 214. Таким образом, НОД(168, 70) = 14.
Числа a
и b
называются равноостаточными (при делении на c
), если равны их остатки.
Для отношения равноостаточности справедливы следующие свойства.
Свойство 1. a и b равноостаточны (при делении на c ) тогда и только тогда, когда a – b делится на c .
Доказательство очевидно.
Свойство 2.
Если a
1, … , a
n
b
1, … , b
n
, то a
1 + … +
a
n
и b
1 + … + b
n
также равноостаточны.
Доказательство очевидно.
Свойство 3.
Если a
1, … , a
n
соответственно равноостаточны c b
1, … , b
n
, то a
1… a
n
и b
1… b
n
также равноостаточны.
Доказательство проведем индукцией по n
. Для n
=1 утверждение очевидно. Покажем его справедливость для двух сомножителей, т. е. для n
=2. Имеем a
1a
2 – b
1b
2 = (a
1 – b
1)a
2 + b
1(a
2 – b
2). Поэтому, если a
1 – b
1 делится на c
и a
2 – b
2 делится на c
, то и a
1a
2 – b
1b
2 делится на c
. Предположим, что утверждение верно для n
– 1 и докажем, что оно верно для n
. Представим произведения a
1… a
n
и b
1… b
n
в виде a
1… a
n
= (a
1… a
n
-1)an
и b
1… b
n
=
(b
1… b
n
-1)bn
. По предположению индукции, a
1… a
n
-1 и b
1… b
n
-1 равноостаточны. Применяя доказанное утверждение для двух сомножителей, получаем, что числа (a
1… a
n
-1)an
и (b
1… b
n
-1)bn
равноостаточны.
Следствие.
Если a
и b
равноостаточны, то a
n
и b
n
равноостаточны.
Заметим, что равноостаточность чисел a
n
и b
n
можно доказать и непосредственно, воспользовавшись формулой a
n
– b
n
= (a
– b
)(an
-
1 + an
-2b
+ … + abn
-2 + bn
-1).
Рассмотрим примеры решения задач на использование этих свойств.
Пример 1.
Выяснить, делится ли на три число 1316–
Решение.
Число 13 при делении на 3 равноостаточно с 1, следовательно, 1316 вравносостаточно с 116 = 1. Число 2 равноостаточно с –1, следовательно 225 с (-1)25 = -1. Число 5 равноостаточно с –1, следовательно, 515 равноостаточно с (-1)15 = -1. Таким образом, число 1316 – 225 515 равноостаточно с 1 – (-1)(-1) = 0, т. е. данное число делится на 3.
Пример 2.
Доказать, что число 1110 – 1 делится на 100.
Решение.
Имеем 1110 – 1 = 10(119 + 118+ … + 1). Число 11 при делении на 10 равноостаточно с 1. Поэтому сумма чисел, стоящих в скобке правой части равноостаточна с 1 + 1 + … + 1 = 10 и, следовательно, делится на 10. Таким образом, исходное число делится на 100.
Пример 3.
Доказать, что при любом натуральном n
число n
3 +
11n
делится на 6.
Решение.
11n
при делении на 6 равноостаточно с –n
. Поэтому данное число равноостаточно с n
3 – n = n
(n –
1) (n +
1).
В правой части стоит произведение трех последовательных натуральных чисел (или 0). Одно из них обязательно четное, а другое делится на 3. Таким образом все произведение делится на 6.
Пример 4.
Доказать, что число + делится на 7.
Решение.
2222 и –4 при делении на 7 равноостаточны, 5555 и 4 также равноостаточны. Поэтому + равноостаточно с -45555 + 42222 = -42222(43333 – 1) = -42222(641111 – 1) = (641110+…+1). Так как 63 делится на 7, то и данное число делится на 7.
Пример 5.
Найти остаток от деления числа на 7.
Решение.
Заметим, что 1000 при делении на 7 равноостаточно с –1. Поэтому ![]() равноостаточно с –10. Последующие слагаемые также равноостаточны с –10 и, значит, вся сумма равноостаточно с числом –100, которое, в свою очередь, равноостаточно с 5. Таким образом, искомый остаток равен 5.
равноостаточно с –10. Последующие слагаемые также равноостаточны с –10 и, значит, вся сумма равноостаточно с числом –100, которое, в свою очередь, равноостаточно с 5. Таким образом, искомый остаток равен 5.
Пример 6. Можно ли 2006 представить как разность квадратов двух натуральных чисел?
Ответ. Нет. Если бы 2006 = a 2 – b 2 = (a – b )(a + b ), то или a – b или a + b было бы четным числом. Но тогда и другое число было бы четным, а значит, a 2 – b 2 делилось бы на 4. Но 2006 не делится на 4.
Рассмотрим теперь некоторые признаки делимости.
1. Признак делимости на 2.
Число делится на 2, если число, образованное его последней цифрой в десятичной записи делится на 2.
2. Признак делимости на 4.
Число делится на 4, если число, образованное двумя последними цифрами в его десятичной записи, делится на 4.
Доказательство вытекает из того, что число 100 и его кратные делятся на 4.
3. Признак делимости на 5.
Число делится на 5, если его последняя цифра в десятичной записи 0 или 5.
4. Признак делимости на 3.
Число делится на 3, если сумма чисел, образованных его цифрами в десятичной записи делится на 3.
Доказательство.
Число 10 равноостаточно с 1. Поэтому 100 равноостаточно с 1, 1000 равноостаточно с 1 и т. д. Таким образом, число a
n
…a
1a
0 = a
0 + a
110 +…+a
n
10n
равноостаточно с a
0+a
1+ … +a
n
.
Заметим, что мы доказали несколько больше, чем требовалось, а именно, мы доказали, что число дает при делении на три такой же остаток, что и сумма чисел, образованных цифрами этого числа в десятичной записи.
5. Признак делимости на 9.
Число делится на 9, если сумма чисел, образованных его цифрами в десятичной записи делится на 9.
Доказательство аналогично предыдущему.
6. Признак делимости на 8.
Число делится на 8, если число, образованное последними тремя цифрами в десятичной записи делится на 8.
Доказательство вытекает из того, что число 1000 и его кратные делятся на 8.
7. Признак делимости на 11.
Число делится на 11, если алгебраическая сумма чисел, образованных его цифрами в десятичной записи с чередующимися знаками делится на 11.
Доказательство.
Число 10 равноостаточно с –1. Поэтому 100 равноостаточно с (-1)(-1) = 1, 1000 равноостаточно с –1 и т. д. Таким образом, число a
n
…a
1a
0= a
0 + a
110 +…+a
n
10n
равноостаточно с a
0 – a
1 + … +
(-1)n
a
n
.
В качестве примера рассмотрим число 3516282. Алгебраическая сумма его цифр равна 2 – 8 + 2 – 6 + 1 – 5 + 3 = -11. Таким образом, данное число делится на 11.
8. Объединенный признак делимости на 7, 11 и 13.
Число делится на 7, 11 или 13, если алгебраическая сумма чисел, образованных тройками цифр данного числа в десятичной записи с чередующимися знаками делится соответственно на 7, 11 или 13.
Доказательство.
Заметим, что произведение чисел 7, 11 и 13 равно 1001. Поэтому число 1000 при делении на 7, 11 или 13 равноостаточно с –1. Далее поступаем как и в признаке делимости на 11.
В качестве примера рассмотрим числоЧисло 295 – 623 + 42 = -286 делится на 11 и 13, но не делится на 7. Следовательно, и данное число делится на 11 и 13, но не делится на 7.
9. Признак делимости на 37.
Число делится на 37, если сумма чисел, образованных тройками цифр данного числа в десятичной записи делится соответственно на 37.
Доказательство вытекает из того, что число 1000 при делении на 37 равноостаточно с 1.
Заметим также, что трехзначные числа 111, 222, …, 999 делятся на 37.
Легко видеть, что числа, делятся на 37.
Воспользуемся свойствами делимости для решения следующей задачи, предлагавшейся на творческом конкурсе учителей математики г. Москвы в 2004 г.
Задача.
На доске написано число.... Разобьем его десятичную запись произвольным образом на два числа и сложим их. С полученными числами проделаем аналогичную операцию и так до тех пор пока не получим однозначное число. Какие однозначные числа можно получить таким образом?
Решение.
Пусть десятичная запись данного числа разбита на числа x
и y.
Тогда исходное число имеет вид x
10...0 + y
, а число, полученное в результате указанной операции равно x + y
. Рассмотрим разность этих чисел: (x
10...0 + y
) - (x + y
) = 9...9x.
Так как эта разность делится на 9, то исходное и полученное число имеют одинаковые остатки при делении на 9. Следовательно, каждый раз, при выполнении указанной операции этот остаток не изменяется. Непосредственная проверка показывает, что остаток от деления на 9 исходного числа равен 2. Значит, в результате указанных операций можно получить только число 2.
Упражнения
1. На какую цифру оканчивается число: а) 99999; б) 3999; в) 71000; г) 3377 + 7733?
2. Докажите, что произведение любых трех последовательных натуральных чисел делится на 6.
3. Докажите, что произведение любых пяти последовательных натуральных чисел делится на 120.
4. Найдите все натуральные числа n > 1, для которых n 3 – 3 делится на n – 1.
5. Докажите, что для любого натурального n число n 3 + 2n делится на 3.
6. Докажите, что для любого натурального n число n 5 + 4n делится на 5.
7. Докажите, что для любого натурального n число n 2 + 1 не делится на 3.
8. Докажите, что для любого натурального n число n 3 + 2 не делится на 9.
9. Докажите, что для любого четного натурального n число n 3 – 4n делится на 48.
10. Докажите, что для любого нечетного натурального n число n 6 – n 4 – n 2 + 1 делится на 128.
11. Докажите, что при любых целых a и b число a 2 + 9ab + b 2 делится на 11.
12. Докажите, что если a 2 + 9ab + b 2 делится на 11, то число a 2 – b 2 делится на 11.
13. Докажите, что если 56a = 65b , то число a + b составное.
14. Докажите, что если число 3n + 2m делится на 23, то и число 17n + 19m делится на 23.
15. Докажите, что число 31974 + 51974 делится на 13.
16. Докажите, что число 2110 – 1 делится на 2200.
17. Докажите, что для любого натурального n число n 2 – 3n + 5 не делится на 121.
18. Пусть S (n ) – сумма цифр в десятичной записи числа n . Найдите все натуральные n , для которых выполняется равенство n + S (n ) + S (S (n )) = 1993.
Литература
1. Воробьев делимости. – М.: Наука, 1980.
2. Математические досуги. – М.: Мир, 1972.
3. , Фомин математические кружки. – Киров, 1994.
4. Горбачев олимпиадных задач по математике. – М.: МЦНМО, 2004.
5. Кордемский смекалка. – М.: Наука, 1991.
6. Московские математические олимпиады 1993 – 2005 г. Под редакцией. – М.: МЦНМО, 2006.
7. Приглашение в теорию чисел. – М.: Наука, 1980.
8. и др. Избранные задачи и теоремы элементарной математики. Часть 1, арифметика и алгебра. – М – Л.: Гос. изд. техн.-теор. литературы, 1950.
Определение. Пусть даны натуральные числа а и b. Говорят, что число а делится на число b, если существует такое натуральное число q, что a = bq.
В этом случае число b называют делителем числа а, а число а - кратным числа b.
Например, 24 делится на 8, так как существует такое q =3, что 24 = 8·3. Можно сказать иначе: 8 - это делитель числа 24, а 24 есть кратное числа 8. В том случае, когда а делится на b, пишут: а: . b. Эту запись »« читают и так: «а кратно b». Заметим, что понятие «делитель данного числа» следует отличать от понятия «делитель», обозначающего то число, на которое делят. Например, если 18 делят на 5, то число 5 -делитель, но 5 не является делителем числа 18. Если 18 делят 6, то в этом случае понятия «делитель» и «делитель данного числа» совпадают.
Из определения отношения делимости и равенства а = 1·а, справедливого для любого натурального а, вытекает, что 1 является делителем любого натурального числа.
Выясним, сколько вообще делителей может быть у натурального числа а. Сначала рассмотрим следующую теорему.
Теорема 1. Делитель b данного числа а не превышает этого числа, т.е. если
а: . b, то b < а.
Доказательство. Так как а: . b, то существует такое q Є N,что a = bq u, значит, a-b = bq – b= b·(q - 1). Поскольку q Є N,тоq≥ 1. Тогда b· (q - 1) ≥ 0 и, следовательно, b ≤ а.
Из данной теоремы следует, что множество делителей данного числа конечно. Назовем, например, все делители числа 36. образуют конечное множество {1,2,3,4,6,9,12,18,36}.
В зависимости от числа делителей среди натуральных чисел различают простые и составные числа.
Определение. Простым числом называется такое натуральное число, которое имеет только два делителя - единицу и само это число.
Например, число 13- простое, поскольку, у него только два делителя: 1 и 13.
Определение. Составным числом называется такое натуральное число, которое имеет более двух делителей.
Так число 4 составное, у него три делителя: 1,2 и 4.
Число 1 не является ни простым, ни составным числом в связи с тем, что оно имеет только один делитель.
Чисел, кратных данному числу, можно назвать как угодно много, - их бесконечное множество. Так, числа, кратные 4, образуют бесконечный ряд: 4, 8, 12, 16, 20, 24, …, и все они могут быть получены по формуле а = 4q, где q принимает значения 1, 2, 3,....
Нам известно, что отношение делимости обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства.
Теорема 2. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя.
Доказательство. Для любого натурального а справедливо равенство а = а·1. Так как 1 Є N, то, по определению отношения делимости, а: . а.
Теорема 3. Отношение делимости антисимметрично, т.е. если а: . b и а ≠ b,
то b ⁞͞ a.
Доказательство. Предположим противное, т.е. что b⁞ a. Но тогда а ≤ b, согласно теореме, рассмотренной выше.
По условию и а ⁞ . b и а ≠ b. Тогда, по той же теореме, b ≤ а.
Неравенства а ≤ b и b ≤ а будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и теорема доказана.
Теорема 4 . Отношение делимости транзитивно, т.е. если а⁞ b и b⁞ с, то а⁞ с.
Доказательство. Так как а: . b, то существует такое натуральное число q, что a = bq, а так как b⁞ с, то существует такое натуральное число р, что b = ср. Но тогда имеем: a = bq = (cp)q = c(pq)- Число pq - натуральное. Значит, по определению отношения делимости,
а⁞ с.
Теорема 5 (признак делимости суммы). Если каждое из натуральных чисел а 1 , а 2 , ...,а п делится на натуральное число b, то и их сумма a 1 + а 2 + ... + а n делится на это число.
Доказательство. Так как а 1 ⁞ b, то существует такое натуральное число q 1 , что а 1 =bq 1 . Так как а 2 ⁞ b, то существует такое натуральное число q 2 , что а 2 = bq 2 . Продолжая рассуждения, получим, что если а n: . b, то существует такое натуральное число q n , что а п = bq n . Эти равенства позволяют преобразовать сумму а 1 + а 2 + ... +а п в сумму вида bq 1 + bq 2 + ... + bq n . Вынесем за скобки общий множитель b, а получившееся в скобках натуральное число q 1 + q 2 + ... + q n обозначим буквой q. Тогда a 1 + a 2 + ... + a n = b(q 1 + q 2 +... + q n) = bq, т.е. сумма а 1 + а 2 +… + а п оказалась представленной в виде произведения числа b и некоторого натурального числа q. А это значит, что сумма а 1 + а 2 +… + а п делится на b, что и требовалось доказать.
Например, не производя вычислений, можно сказать, что 175 + 360 + 915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.
Теорема 6 (признак делимости разности). Если числа а 1 и а 2 делятся на b и а 1 ≥ а 2 , то их разность а 1 - а 2 делится на b.
Доказательство этой теоремы аналогично доказательству признака делимости суммы.
Теорема 7 (признак делимости произведения). Если число а делится на b, то произведениe вида ах, где х Є N, делитcя на b.
Доказательство. Так как а: . b, то существует такое натуральное число q, что a = bq. Умножим обе части этого равенства на натуральное число х. Тогда ах=(bq)x, откуда на основании свойства ассоциативности умножения (bq)x = b(qx)и, значит, ax = b(qx), где qx - натуральное число. Согласно определению отношения делимости, ax: . b, что и требовалось доказать.
Из доказанной теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b. Например, произведение 24·976·305 делится на 12, так как на 12 делится множитель 24.
Рассмотрим еще три теоремы, связанные с делимостью суммы и произведения, которые часто используются при решении задач на делимость.
Теорема 8. Если в сумме одно слагаемое не делится на число b, а все остальные слагаемые делятся на число b, то вся cумма на число b не делится.
Доказательство. Пусть s = а 1 + а г + ... + а п +" с и известно, что а 1: . B, а 2: . B,
а 3: . b, … а n: . b, но с: . b. Докажем, что тогда s: . b
Предположим противное, т.е. Пусть s: . b. Преобразуем сумму s к виду с = s- (а 1 + а 2 +… + а n ). Так как s: . b по предположению, (а 1 + а 2 +… + а n ) : . b согласно признаку делимости суммы, то по теореме делимости разности с: .b
Пришли к противоречию с тем, что дано. Следовательно, s: . b.
Например, сумма 34 + 125 + 376 + 1024 на 2 не делится, так 34: .2,376: .2,124: .2, но 125 не делится на 2.
Теорема 9 . Если в произведении ab множитель a делится на натуральное число т, а множитель b делится на натуральное число n,то ab делится на mn.
Справедливость этого утверждения вытекает из теоремы о делимости произведения.
Теорема 10. Если произведение ас делится на произведение bс, причем с - натуральное число, то и а делится на b.
Доказательство. Так как ас делится на bc, то существует такое натуральное число q, что ас = (bc)q, откуда ас = (bq)c и, следовательно, а = bq, т.е. а : .b.
Упражнения
1. Объясните, почему число 15 является делителем числа 60 и не является делителем числа 70.
2. Постройте граф отношения «быть делителем данного числа», заданного на множестве Х = {2, 6,. 12, 18, 24}. Как отражены на этом графе свойства данного отношения?
3. Известно, что число 24 - делитель числа 96, а число 96 -делитель числа 672. Докажите, что число 24 делитель числа 672, не выполняя деления.
4. Запишите множество делителей числа.
а) 24; 6)13; в) 1.
5 .На множестве X ={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11; 12} задано отношение «иметь одно и то же число делителей». Является ли оно отношением эквивалентности?
6 .Постройте умозаключение, доказывающее, что:
а) число 19 является простым;
б) число 22 является составным.
7. Докажите или опровергните следующие утверждения:
а) Если сумма двух слагаемых делится на некоторое число, то и каждое слагаемое делится на это число.
б) Если одно из слагаемых суммы не делится на некоторое число, то и сумма не делится на это число.
в) Если ни одно слагаемое не делится на некоторое число, то и сумма не делится на это число.
г) Если одно из слагаемых суммы делится на некоторое число, а другое не делится на это число, то и сумма не делится на это число.
8. Верно ли, что:
а) а: . ти b: . n =>ab: .mn
б) а: .п и b: .n => ab: .n;
в) ab: .n => а: .п или b: .n.