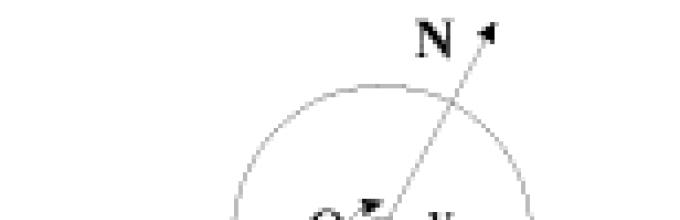1. Уравнение движения центра масс
Особенностью плоского движения является то, что ось вращения сохраняет свою ориентацию в пространстве и остается перпендикулярной плоскости, в которой движется центр масс. Еще раз подчеркнем, что уравнение моментов (3.20) записано относительно, в общем случае, ускоренно движущегося центра масс, однако, как было отмечено в начале лекции, оно имеет такой же вид, как и уравнение моментов относительно неподвижной точки.
В качестве примера рассмотрим задачу о скатывании цилиндра с наклонное плоскости. Приведем два способа решения этой задачи с использованием уравнений динамики твердого тела.
Первый способ. Рассматривается вращение цилиндра относительно оси, проходящее через центр масс (рис. 3.11).
|
|
Система уравнений (3.19 - 3.20) имеет вид:
|
|
К этой системе необходимо добавить уравнение кинематической связи
|
| (3.23) |
Последнее уравнение получается из условия, что цилиндр скатывается без проскальзывания, то есть скорость точки М цилиндра равна нулю.
Уравнение движения центра масс (3.1) запишем для проекций ускорения и сил на ось x вдоль наклонной плоскости, а уравнение моментов (3.22) - для проекций углового ускорения и момента силы трения на ось y , совпадающую с осью цилиндра. Направления осей x и у выбраны согласованно, в том смысле, что положительному линейному ускорению оси цилиндра соответствует положительное же угловое ускорение вращения вокруг этой оси. В итоге получим:
|
|
|
| (3.27) |
Следует подчеркнуть, что - сила трения сцепления - может принимать любое значение в интервале от О до (сила трения скольжения) в зависимости от параметров задачи. Работу эта сила не совершает, но обеспечивает ускоренное вращение цилиндра при его скатывании с наклонной плоскости. В данном случае
Качение без проскальзывания определяется условием
Мгновенная ось вращения проходит через точку соприкосновения цилиндра и плоскости (точку М). При таком подходе отпадает необходимость в уравнении движении центра масс и уравнении кинематической связи. Уравнение моментов относительно мгновенной оси имеет вид:
|
| (3.33) |
Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:
|
| (3.37) |
где - скорость центра масс тела, - скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:
| (3.38) |
так как (суммарный импульс частиц в системе центра масс равен нулю).
Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.
В этой связи задачу о скатывании цилиндра с наклонной плоскости можно решить, используя закон сохранения механической энергии (напомним, что сила трения при качении без проскальзывания работу не совершает).
Приращение кинетической энергии цилиндра равно убыли его потенциальное энергии:
Дифференцируя обе части этого уравнения по времени, получим
|
| (3.41) |
откуда для линейного ускорения оси цилиндра будем иметь то же выражение, что и при чисто динамическом способе решения (см. (3.27, 3.36)).
Замечание. Если цилиндр катится с проскальзыванием, то изменение его кинетической энергии будет определяться также и работой сил трения. Последняя, в отличие от случая, когда тело скользит по шероховатой поверхности, не вращаясь, определяется, в соответствии с (3.14), полным углом поворота цилиндра, а не расстоянием, на которое переместилась его ось.
Заключение
Динамика твердого тела на данном этапе используется для тел, движущихся в сплошной среде.
В задаче о полете тела с тремя несущими поверхностями при наличии динамической асимметрии определены условия, при которых проявляются синхронизмы 1:3. С увеличением угловой скорости вращения тела около продольной оси даже на поверхности рассеивания заметно ослабление этого эффекта.
Разработана программа имитационного моделирования комплекса задач по динамике полета противоградовых ракет. С ее помощью построены таблицы введения поправок на установочные углы запуска ракет для наилучшей компенсации вредного влияния ветра.
Создана механико-математическая модель полета бумеранга. Открыта лаборатория навигации и управления.
Разработан и внедрен на аэродинамической трубе А-8 комплекс механического оборудования и сопутствующей измерительной аппаратуры для проведения динамических испытаний моделей. Определены коэффициенты демпфирования поперечных колебаний осесимметричных оперенных тел различного удлинения при раскрутке вокруг собственной оси в до- и сверхзвуковом потоках.
На основе численного решения задачи о плоских движениях аэродинамического маятника (с несущей поверхностью в виде прямоугольной пластины) в несжимаемой жидкости с учетом динамики вихрей определены области существования всех типов движения маятника, включая режимы автоколебаний и авторотации. Открыта лаборатория сверхзвуковой аэродинамики.
Также в институте компьютерных исследований проводят значимые исследования по динамике твердого тела.
Это направление исследований института связано с анализом движения твердого тела с широким применением компьютерных методов.
Компьютерные исследования в динамике твердого тела относятся к отдельной области науки - компьютерной динамике, которая устанавливает общие закономерности движения систем при помощи различных численных методов и алгоритмов.
В сочетании с аналитическими методами, достижениями топологии, анализа, теории устойчивости и других методов компьютерная динамика применяется, главным образом, в исследовании интегрируемых задач, в частности, динамических проблем теории волчков. Такой подход позволяет получить достаточно полное представление о движении, разобраться во всем его многообразии и наглядно представить себе каждое конкретное движение и его особенности.
Помимо анализа интегрируемых ситуаций в институте начато исследование случаев хаотического поведения в динамике твердого тела. Эти исследования, которые ранее почти не проводились, основаны на широком применении высокоточного компьютерного моделирования. Ожидается, что изучение этой области динамики твердого тела позволит получить в перспективе много новых интересных результатов.
Кроме того, в институте проводятся исследования с использованием методов пуассоновой динамики и геометрии, теории групп и алгебр Ли - методов, которые во многом возникли из задач динамики твердого тела.



ВПО «ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Факультет общих математических и естественнонаучных дисциплин Кафедра общей физики ЛАБОРАТОРНАЯ РАБОТА №23 Проверка основного закона динамики вращательного движения твердого тела относительно неподвижной оси выполнил: студент гр. 5СКб-11 Череповец, 2009/10 уч. Год проверил: ассис. Герасимов Р.А. Введение...

е является проблема лазерного охлаждения твердых тел. При комнатной температуре атомы и молекулы, из которых состоит воздух, двигаются в различных направлениях со скоростью около 4000км/час. Такие атомы и молекулы трудно изучать, потому что они слишком быстро исчезают из области наблюдения. Понижая температуру, можно уменьшить скорость, однако проблема состоит в том, что при охлаждении газы обычно...
Основной закон динамики можно записать в иной форме, зная понятие центра масс системы:
Это есть уравнение движения центра масс системы , одно из важнейших уравнений механики. Оно утверждает, что центр масс любой системы частиц движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы .
Ускорение центра масс системы совершенно не зависит от точек приложения внешних сил.
Если , то , значит и - это случай замкнутой системы в инерциальной системе отсчета. Таким образом, если центр масс системы движется равномерно и прямолинейно, это означает, что её импульс сохраняется в процессе движения.
Пример: однородный цилиндр массы и радиуса скатывается без скольжения по наклонной плоскости, составляющей угол с горизонтом. Найти уравнение движения?
| |
Совместное решение дает значение параметров
Уравнение движения центра масс совпадает с основным уравнением динамики материальной точки и является его обобщением на систему частиц: ускорение системы как целого пропорционально результирующей всех внешних сил и обратно пропорционально массе системы .
Систему отсчета, жестко связанную с центром масс, которая движется поступательно относительно ИСО называют системой центра масс. Ее особенностью является то, что полный импульс системы частиц в ней всегда равен нулю, так, как .
Конец работы -
Эта тема принадлежит разделу:
Кинематика поступательного движения
Физические основы механики.. кинематика поступательного движения.. механическое движение формой существования..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Все темы данного раздела:
Механическое движение
Материя, как известно, существует в двух видах: в виде вещества и поля. К первому виду относятся атомы и молекулы, из которых построены все тела. Ко второму виду относятся все виды полей: гравитаци
Пространство и время
Все тела существуют и движутся в пространстве и времени. Эти понятия являются основополагающими для всех естественных наук. Любое тело имеет размеры, т.е. свою пространственную протяженность
Система отсчета
Для однозначного определения положения тела в произвольный момент времени необходимо выбрать систему отсчета - систему координат, снабженнуя часами и жестко связаннуя с абсолютно твердым телом, по
Кинематические уравнения движения
При движении т.М ее координаты и меняются со временем, поэтому для задания закона движения необходимо указать вид фун
Перемещение, элементарное перемещение
Пусть точка М движется от А к В по криволинейному пути АВ. В начальный момент ее радиус-вектор равен
Ускорение. Нормальное и тангенциальное ускорения
Движение точки характеризуется также ускорением-быстротой изменения скорости. Если скорость точки за произвольное время
Поступательное движение
Простейшим видом механического движения твердого тела является поступательное движение, при котором прямая, соединяющая любые две точки тела перемещается вместе с телом, оставаясь параллельной| сво
Закон инерции
В основе классической механики лежат три закона Ньютона, сформулированные им в сочинении «Математические начала натуральной философии», опубликованном в 1687г. Эти законы явились результатом гениал
Инерциальная система отсчета
Известно, что механическое движение относительно и его характер зависит от выбора системы отсчета. Первый закон Ньютона выполняется не во всех системах отсчета. Например, тела, лежащие на гладком п
Масса. Второй закон Ньютона
Основная задача динамики заключается в определении характеристик движения тел под действием приложенных к ним сил. Из опыта известно, что под действием силы
Основной закон динамики материальной точки
Уравнение описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно
Третий закон Ньютона
Наблюдения и опыты свидетельствуют о том, что механическое действие одного тела на другое является всегда взаимодействием. Если тело 2 действует на тело 1, то тело 1 обязательно противодействует те
Преобразования Галилея
Они позволяют определить кинематические величины при переходе от одной инерциальной системы отсчета к другой. Возьмем
Принцип относительности Галилея
Ускорение какой-либо точки во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно одинаково:
Сохраняющиеся величины
Любое тело или система тел представляют собой совокупность материальных точек или частиц. Состояние такой системы в некоторый момент времени в механике определяется заданием координат и скоростей в
Центр масс
В любой системе частиц можно найти точку, называемую центром масс
Консервативные силы
Если в каждой точке пространства на частицу, помещенную туда, действует сила, говорят, что частица находится в поле сил, например в поле сил тяжести, гравитационной, кулоновской и других сил. Поле
Центральные силы
Всякое силовое поле вызвано действием определенного тела или системы тел. Сила, действующая на частицу в этом поле об
Потенциальная энергия частицы в силовом поле
То обстоятельство, что работа консервативной силы (для стационарного поля) зависит только от начального и конечного положений частицы в поле, позволяет ввести важное физическое понятие потенциально
Связь между потенциальной энергией и силой для консервативного поля
Взаимодействие частицы с окружающими телами можно описать двумя способами: с помощью понятия силы или с помощью понятия потенциальной энергии. Первый способ более общий, т.к. он применим и к силам
Кинетическая энергия частицы в силовом поле
Пусть частица массой движется в силов
Полная механическая энергия частицы
Известно, что приращение кинетической энергии частицы при перемещении в силовом поле равно элементарной работе всех сил, действующих на частицу:
Закон сохранения механической энергии частицы
Из выражения следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться
Кинематика
Поворот тела на некоторый угол можно
Момент импульса частицы. Момент силы
Кроме энергии и импульса существует ещё одна физическая величина, с которой связан закон сохранения - это момент импульса. Моментом импульса частицы
Момент импульса и момент силы относительно оси
Возьмем в интересующей нас системе отсчета произвольную неподвижную ось
Закон сохранения момента импульса системы
Рассмотрим систему, состоящую из двух взаимодействующих частиц, на которые действуют также внешние силы и
Таким образом, момент импульса замкнутой системы частиц остается постоянным, не изменяется со временем
Это справедливо относительно любой точки инерциальной системы отсчета: . Моменты импульса отдельных частей системы м
Момент инерции твердого тела
Рассмотрим твердое тело, которое мож
Уравнение динамики вращения твердого тела
Уравнение динамики вращения твердого тела можно получить, записав уравнение моментов для твердого тела, вращающегося вокруг произвольной оси
Кинетическая энергия вращающегося тела
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами
Работа вращения твердого тела
Если тело приводится во вращение силой
Центробежная сила инерции
Рассмотрим диск, который вращается вместе с шариком на пружине, надетой на спицу, рис.5.3.
Шарик находится
Сила Кориолиса
При движении тела относительно вращающейся СО, кроме, появляется ещё одна сила-сила Кориолиса или кориолисова сила
Малые колебания
Рассмотрим механическую систему, положение которой может быть определено с помощъю одной величины, например х. В этом случае говорят, что система имеет одну степень свободы.Величиной х может быть
Гармонические колебания
Уравнение 2-го Закона Нъютона в отсутствие сил трения для квазиупругой силы вида имеет вид:
Математический маятник
Это материальная точка, подвешенная на нерастяжимой нити длиною, совершающая колебания в вертикальной плоск
Физический маятник
Это твердое тело, совершающее колебания вокруг неподвижной оси, связанной с телом. Ось перпендикулярна рисунку и нап
Затухающие колебания
В реальной колебательной системе имеются силы сопротивления, действие которых приводят к уменьшению потенциальной энергии системы, и колебания будут затухающими.В простейшем случае
Автоколебания
При затухающих колебаниях энергия системы постепенно уменьшается и колебания прекращаются. Для того, чтобы их сделать незатухающими, необходимо пополнять энергию системы извне в определенные момент
Вынужденные колебания
Если колебательная система, кроме сил сопротивления, подвергается действию внешней периодической силы, изменяющейся по гармоническому закону
Резонанс
Кривая зависимости амплитуды вынужденых колебаний от приводит к тому, что при некоторой определенной для данной систе
Распространение волн в упругой среде
Если в каком либо месте упругой среды (твёрдой, жидкой, газообразной) поместить источник колебаний, то из-за взаимодействия между частицами колебание будет распространяться в среде от частицы к час
Уравнение плоской и сферической волн
Уравнение волны выражает зависимость смещения колеблющейся частицы от ее кординат,
Волновое уравнение
Уравнение волны является решением дифференциального уравнения, называемого волновым.
Для его установления найдем вторые частные производные по времени и координатам от урав
В любой системе материальных точек, а следовательно, и системе тел имеется одна замечательная точка С, которая называется центром масс илицентром инерции системы. Ее положение определяется радиусом-вектором r c :
Для центра масс справедливо следующее утверждение: при движении любой системы частиц ее центр масс движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены всевнешние силы, действующие на систему. По форме уравнение движения центра масс совпадает со вторым законом Ньютона:
где - ускорение центра масс.
Уравнение динамики вращательного движения
При вращательном движении твердого тела аналогом второго закона Ньютона является основное уравнение динамики вращательного движения , которое имеет вид:
где e - угловое ускорение, М - суммарный момент сил относительно оси вращения. Если момент инерции тела изменяется в процессе движения, то нужно применять этот закон в следующей форме:
где - момент импульса твердого тела.
Любое движение твердого тела может быть представлено как наложение двух основных видов движения - поступательного и вращательного. Например, качение шара можно рассматривать как перемещение с ускорением, равным ускорению центра масс, и вращение относительно оси, проходящей через центр масс. Каждое движение подчиняется, как показано в таблице 5, соответствующему закону.
Законы динамики в неинерциальных системах отсчета.
Силы инерции
Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называются неинерциальными (НИСО) , и в них не выполняются рассмотренные выше законы динамики: второй закон Ньютона, уравнение движения центра масс, уравнение динамики вращательного движения. Однако их можно сохранить и для неинерциальных систем, если кроме обычных сил взаимодействия F ввести еще “силы” особой природы F ин , называемые силами инерции . Их введение обусловлено ускорением движения неинерциальной системы отсчета относительно инерциальной.
Законы динамики Таблица 5
| Физическая ситуация | Применяемые законы |
| Прямолинейное движение материальной точки, поступательное движение твердого тела | Второй закон Ньютона |
| Движение материальной точки по окружности или другой криволинейной траектории | Второй закон Ньютона |
| Вращение твердого тела вокруг неподвижной оси | Основной закон динамики вращательного движения |
| Сложное движение твердого тела | Уравнение движения центра масс и уравнение динамики вращательного движения |
В НИСО законы динамики примут вид:
второй закон Ньютона + ;
уравнение движения центра масс + ;
уравнение динамики вращательного движения + .
Существует два основных типа неинерциальных систем. Обозначим символом К инерциальную систему отсчета, а - неинерциальную .
1. движется относительно К с постоянным ускорением . В этом случае в уравнениях динамики следует ввести силу инерции , равную = - m a c . Точкой приложения этой силы считать центр масс.
Точка С , положение которой определяется радиус-вектором:
называется центром масс системы материальных точек. Здесь m i - масса i -й частицы; r i - радиус-вектор, задающий положение этой частицы; - суммарная масса системы. (Отметим, что в однородном поле сил тяжести центр масс совпадает с центром тяжести системы.)
Продифференцировав r C по времени, найдем скорость центра масс:
где V i - скорость i -ой материальной точки, p i - ее импульс, P – импульс системы материальных точек. Из (2.18) следует, что суммарный импульс системы есть
P = mV C , (2.19)
Из (2.19) и (2.16), получим уравнение движения центра масс:
(а C – ускорение центра масс). Таким образом, из уравнения
следует, что центр масс движется так, как двигалась бы материальная точка с массой, равной массе системы, под действием результирующей всех внешних сил, приложенных к телам системы. Для замкнутой системы а C = 0. Это означает, что центр масс замкнутой системы движется прямолинейно и равномерно либо покоится .
Система отсчета, относительно которой центр масс покоится, называется системой центра масс (сокращенно ц- системой). Эта система является инерциальной.
Контрольные вопросы
1. В каких системах отсчета справедливы законы Ньютона?
2. Какие формулировки второго закона Ньютона вы знаете?
3. Чему равен вес свободно падающего тела?
4. Какой знак имеет скалярное произведение силы трения и скорости тела?
5. Чему равен импульс системы материальных точек в системе центра масс?
6. Чему равно ускорение центра масс тела, имеющего массу m и находящегося под действием сил ?
1. Пуля пробивает две примыкающие друг к другу коробки с жидкостями: вначале коробку с глицерином, затем такую же коробку с водой. Как изменится конечная скорость пули, если коробки поменять местами? Другими силами, действующими на пулю, кроме силы сопротивления жидкости F = – rV , пренебречь.
2. Движение материальной точки задано уравнениями x = at 3 , y = bt.
3. Скорость материальной точки задана уравнениями u x = A ∙ sinwt ,u y = A ∙ coswt. Изменяется ли сила, действующая на точку: а) по модулю; б) по направлению?
4. Шарик, висящий на нити длиной l , после горизонтального толчка поднимается на, высоту H , не сходя с окружности. Может ли его скорость оказаться равной нулю: а) при H < l б) при H > l ?
5. Два тела массами т 1 > m 2 падают с одинаковой высоты. Силы сопротивления считать постоянными и одинаковыми для обоих тел. Сравнить время падения тел.
6. Два одинаковых бруска, связанные нитью, движутся по горизонтальной плоскости под действием горизонтальной силы F . Зависит ли сила натяжения нити: а) от массы брусков; б) от коэффициента трения брусков о плоскость?
7. Брусок массой m 1 = 1 кг покоится на бруске массой m 2 = 2 кг. На нижний брусок начала действовать горизонтальная сила, возрастающая пропорционально времени, ее модуль F = 3t (F – в Н, t – в с). В какой момент времени верхний брусок начнет проскальзывать? Коэффициент трения между брусками m = 0,1, трение между нижним бруском и опорой пренебрежимо мало. Принять g = 10 м/с 2 .
8. Два шарика а и б, подвешенные на нитях в общей точке0, равномерно движутся по круговым траекториям, лежащим в одной горизонтальной плоскости. Сравнить их угловые скорости.
9. Коническая воронка вращается с постоянной угловой скоростью w. Внутри воронки на стенке лежит тело, которое может свободно скользить вдоль образующей конуса. При вращении тело находится в равновесии относительно стенки. Является это равновесие устойчивым или неустойчивым?
Глава 3
Работа и энергия
Уравнение движения центра масс в векторной форме
Положение и движение самолета в полете определяют относительно поверхности Земли. Поэтому за основную систему отсчета, принимают геоцентрическую неинерциальную систему координат, связанную с Землей и совершающую вместе с ней суточное
вращение с угловой скоростью со3 (земная система отсчета).
Движение центра масс самолета описывается динамическим
уравнением (1.7), которое после подстановки FBIi = RA + mgr примет вид
m^^P + RA + mgr + F’ + F*, (1.32)
где 1/к - вектор скорости движения центра масс самолета относи-
тельно Земли и gr - вектор гравитационного ускорения.
Переносную и кориолисову силы инерции, связанные с вращением Земли, определяют известными из теоретической механики выражениями
Fe - - mWe == - m
KK = - m#K = - 2m(to3 x VK), . (1.33)
где r -- радиус-вектор, проведенный из начала геоцентрической системы отсчета 0° в центр масс самолета; We и И7К - переносное и кориолисово ускорения центра масс, обусловленные вращением выбранной геоцентрической системы отсчета относительно инерциальной. ‘ .., .
Поскольку в справочных таблицах обычно приводятся значения ускорения свободного падения с учетом переносной силы инерции в зависимости от высоты, то в правой части уравнения (1.32) можно
геометрическую сумму сил гравитационного притяжеция. mgr и переносной силы инерции F1 заменить силой тяжести G:
G = mgt + Fe - mg. (1-34)
В (1.34) g-вектор результирующего ускорения свободного падения и центробежной силы,.
Векторное уравнение (1,32) с учетом (1.34) запишем в виде
т^г=? + ^ + ®1+?к — О-35)
Как было указано в § 1.1, при практическом применении векторное уравнение движения проектируется на оси прямоугольной системы координат. Выбор систёмы координат для составления-дифференциальных уравнений движения центра масс самолета определяется задачей исследования. При исследовании траекторий обычно применяют траекторные оси. В то же время задачи устойчивости и управляемости удобнее рассматривать в связанной системе координат.
Уравнения движения центра масс в траекторией системе координат
Наиболее простую и удобную форму система динамических уравнений движения центра масс самолета (поступательного движения) примет, если векторное уравнение (1.35) спроектировать на оси траекторной системы координат.
Применяя формулы (1.9) для проектирования левой части уравнения (1.35) и учитывая, что 1/*„ = VI:, Vm = Vzi: =0, получим
тУк = Рхи Г Ххк ~Ь GXK ~Ь Р*к‘> тыг^Ук - Р!,к г Уi; b G,;K — F(1.36) - тыугУК - РZK “Ь ~Ь GZK ф F*к,
где (оун, согк - проекции на траекторные оси вектора угловой ско-
рости (о„ вращения траекторной системы координат относительно Земли; в правой части приведены проекции соответствующих сил на траекторные оси.
Для написания этих уравнений в развернутом виде необходимо
найти проекции угловой скорости сок, а также проекции кориоли-
совой силы инерции FK на траекторные оси. Проекции внешних сил и тяги на эти оси были определены в § 1.6.
Угловую скорость со„ можно представить в виде суммы переносной
угловой скорости сокр нормальной системы 0XgYgZg в системе от-
счета O^X^YqZq и угловой скорости сок& вращения скоростной системы относительно нормальной:
сон = соКр -|- coKg. (1.37)
Переносная угловая скорость сокр, в свою очередь, может быть представлена суммой угловых скоростей:
Шкр -Я-ф-ф, (1.38)
где К - угловая скорость поворота меридиональной плоскости,
Угловая скорость coKg также может быть представлена в виде
суммы угловой скорости Фг вокруг ОСИ OYg и угловой скорости 0 вокруг оси OZg (см. рис. 1.5):
Используя табл. I (см. приложение) направляющих косинусов, находим проекции вектора сок на оси OY„ и OZK траекторной системы
co^j, = Я (sin ер cos 0 - cos ф sin Y sin 0) ф sin Y sin 0 + !F cos 0;
согк = Я, cos ф sin V - ф cos V ~f — 0, (1-40)
которые после подстановки выражений (1.21) в результате несложных преобразований будут иметь вид
gj,(K = ¥ cos 0 V sin 4r cos20 tg ф/(/?з — f Я);
co2K = 0 - И cos Q/(R3 + Я). (1.41)
Найдем теперь проекции кориолисовой силы инерции на траек — торные оси. Вектор кориолисовой силы инерции определяется известной из механики формулой
FK ~ - mwK = - 2т(и3 х Кк) (1-42)
и перпендикулярен (03 и Ук.
Проекции кориолисовой силы инерции на оси траекторной системы выражаются формулами
Кк = 0; FyK = 2ma>aVR cos ф cos
F*к = 2mcoaVK (sin ф cos 0 - cos ф sin ‘P sin 0).
Подставляя в (1.36) выражения для проекций угловых скоростей, определенные формулами (1.41), проекции тяги, аэродинамической силы, силы тяжести (см. формулы (1.27) и (1.28), а также (1.30)) и проекции кориолисовой силы инерции, выраженные формулами (1.43), получим систему динамических уравнений движения центра масс самолета относительно сферической вращающейся Земли в проекциях на оси траекторной системы координат (при отсутствии ветра ук = V, ¥ = фи):
mV - Р cos (а + ф,) cos р - Ха - mg sin 0; (1.44)
mVQ = Р = пха
п1т = Р fsln (« + COS Уа + cos (о — f Фя) Stalin уа1 +
Ya cos у a - Zu sin Y0} = nya cos у a - nzU sin ya nzк = -^{p фР) sin p cos yJ h + У a sin ya + Za cos = tiya sin Yn + «го COS Yo-
В (1.49) и (1.50) аэродинамические силы определены в скоростной системе осей координат. .
‘ Разделив левые и правые части уравнений (1.44) … (1.46) на О = mg, получим динамические уравнения движения центра масс в перегрузках
V ?= пХа - sin 0;
Jr ё = tlya COS Yu — «za Sin Yu - COS 0 |-
f - cos ф sin ¥ (/?з + //)’. (1.51)
——— - і = nya sin Yu - «70 cos Ya H — - C0B к (simp cos 0 -
Cos ф cos ¥ sin 0) - Vі cosE0 sin ¥ tg
‘При рассмотрении частных случаев движения самолета выражения для проекций перегрузки значительно упрощаются.
Для]) полета без скольжения (ft == О, Za = 0) с малыми углами атаки, когда можно принять sin (a + фР) « а + фР, cos (os + + Фр) » 1, формулы (1.49) и (1.50) примут вид
Р-Ха. .. Р(а + Фр) + Ко. ха~ mg ■’ пч°~ Ищ *
пга = 0 (1,52)
и, без ветра, " ‘ 1 ‘ ■
«жк ~ «зса» пу* =.■«№COS Yu’.. «Лі = «j/аSin Yu — (15)
В проекциях на связанные оси вектор перегрузки может быть представлен составляющими пх, пу и nz, которые называются продольной, нормальной и поперечной перегрузкой соответственно. Используя таблицу направляющих косинусов, получим
Пх = пха COS a COS Р + пиа sin о - nzu cos os Sin Р; 4
пу - - пха sin a cos Р -)- пуа cos a + пга sin a sin P; (1-54) «г = nxa Si» P + «га cos P-
§ 1.8. ДИНАМИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ САМОЛЕТА ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
Исследование движения самолета относительно центра масс (вращательного,- илн углового) удобно выполнять, если использовать динамические уравнения в проекциях на оси связанной системы координат 0XYZ. При изучении углового движения само-
лета так же, как и при определении траекторий центра масс, применяют в качестве системы отсчета неинерциальную систему, связанную с Землей.
Проектируя векторное уравнение (1.8) на оси связанной системы координат и применяя формулы (1.9) для вычисления проекций производных по времени от вектора кинетического момента самолета, получим систему скалярных уравнений движения самолета относительно центра масс (вращательного, или углового движения)
*§.- + coyKz-a>zKy = MRx)
J — агКх ьзхКг = Мру’, (1.55)
Rff — + ЫхКу - Ь)1/Кх = Мрг,
где К. х, К у, Кг - проекции вектора кинетического момента самолета на связанные оси координат; (ох, ыу, (oz - проекции вектора угловой скорости самолета относительно Земли на те же оси; MRx, MRu, MRz - проекции результирующего момента аэродинамических сил и тяги относительно центра масс на те же оси. Следует иметь в виду, что момент массовых сил (сил тяжести, центробежных и кориолисовых сил инерции) вокруг центра масс самолета равен нулю.
Угловая скорость самолета относительно Земли является суммой векторов угловой скорости самолета относительно нормальной
системы координат и угловой скорости (о«р вращения нормальной системы координат относительно Земли вследствие кривизны поверхности Земли, Для реальных условий полета самолета последняя
составляющая ы„р мала и ею можно пренебречь.
Проекции кинетического момента К на произвольные подвижньЙ! оси записываются в теоретической механике^как /’V-;
Кх JХ^Х ‘ /xytoy /хг(0г)
где /ж, Jy, Jz осевые, а 7*„, Jxz, uJyZ - центробежные моменты инерции, которые определяются формулами:
Jx = J (уг + z) dm Jy - J (Xі — f z-) dm)
Jz = j (Xі + Уъ) dm; Jay = jxy dm
Jxi = j xz dm) Jyz = j t/z dm.
Моменты инерции самолетов с заметно изменяющейся в полете массой являются функциями времени.
Поскольку основная плоскость OXY связанной системы координат является плоскостью симметрии самолета, то в связанных осях центробежные моменты инерции, содержащие координаты г, равны нулю: Jxz — Juz — — 0.
С учетом этого упрощения, используя выражения (1.56), уравнения (1.55), запишем в виде
Jх^х ^ху®у і г ^ у) ^ ху^х^у == рх)
Jу®У ^ху®х (/ж ‘ *^г) ®жВ)г Jx^z == ^Ry’i
Jг Ь (^у ^х) ^[>х^[)у Jxy (Щ* Wp) = Аі рг.
Подробнее выражения для проекций результирующего момента MRx, MRy и MRz будут рассмотрены во второй части книги при анализе углового движения самолета.