1. Jednačina kretanja centra mase
Karakteristika ravninskog kretanja je da os rotacije zadržava svoju orijentaciju u prostoru i ostaje okomita na ravan u kojoj se kreće centar mase. Još jednom naglašavamo da se jednadžba momenata (3.20) piše u odnosu na, u opštem slučaju, ubrzano kretanje centra mase, međutim, kako je napomenuto na početku predavanja, ima isti oblik kao i jednadžba momenata u odnosu na fiksnu tačku.
Kao primjer, razmotrite problem kotrljanja cilindra niz nagnutu ravan. Predstavljamo dva načina rješavanja ovog problema korištenjem jednadžbi dinamike krutog tijela.
Prvi način. Razmatra se rotacija cilindra u odnosu na osu koja prolazi kroz centar mase (slika 3.11).
|
|
Sistem jednačina (3.19 - 3.20) ima oblik:
|
|
Ovom sistemu potrebno je dodati jednačinu kinematičke relacije
|
| (3.23) |
Posljednja jednačina se dobija iz uslova da se cilindar kotrlja bez klizanja, odnosno da je brzina tačke M cilindra nula.
Zapisujemo jednadžbu gibanja centra mase (3.1) za projekcije ubrzanja i sila na x os duž nagnute ravni, a jednadžbu momenata (3.22) za projekcije ugaonog ubrzanja i momenta trenja na os y koja se poklapa sa osom cilindra. Smjerovi x i y osi su odabrani dosljedno, u smislu da pozitivno linearno ubrzanje ose cilindra odgovara pozitivnom kutnom ubrzanju rotacije oko ove ose. Kao rezultat dobijamo:
|
|
|
| (3.27) |
Treba naglasiti da sila trenja kvačila može poprimiti bilo koju vrijednost u rasponu od O do (sila trenja klizanja) ovisno o parametrima problema. Ova sila ne radi nikakav posao, ali osigurava ubrzanu rotaciju cilindra dok se kotrlja niz nagnutu ravninu. U ovom slučaju
Kotrljanje bez klizanja je određeno uslovom
Trenutna os rotacije prolazi kroz tačku kontakta cilindra i ravni (tačka M). Ovakvim pristupom nema potrebe za jednadžbom kretanja centra mase i jednadžbom kinematičke veze. Jednadžba momenata oko trenutne ose ima oblik:
|
| (3.33) |
Kinetička energija čvrste supstance je zbir kinetičkih energija pojedinih čestica:
|
| (3.37) |
gdje je brzina centra mase tijela, brzina i-te čestice u odnosu na koordinatni sistem koji je povezan sa centrom mase i vrši translatorno kretanje s njim. Kvadriranjem sume brzina dobijamo:
| (3.38) |
budući da je (ukupni impuls čestica u sistemu centara mase nula).
Dakle, kinetička energija pri kretanju u ravnini jednaka je zbiru kinetičkih energija translacijskog i rotacijskog kretanja (Königov teorem). Ako ravninsko kretanje posmatramo kao rotaciju oko trenutne ose, tada je kinetička energija tela energija rotacionog kretanja.
S tim u vezi, problem kotrljanja cilindra iz nagnute ravni može se riješiti korištenjem zakona održanja mehaničke energije (podsjetimo da sila trenja ne radi kada se kotrlja bez klizanja).
Povećanje kinetičke energije cilindra jednako je smanjenju njegove potencijalne energije:
Razlikovanjem obe strane ove jednačine u odnosu na vreme, dobijamo
|
| (3.41) |
odakle ćemo za linearno ubrzanje ose cilindra imati isti izraz kao kod čisto dinamičke metode rješenja (vidi (3.27, 3.36)).
Komentar. Ako se cilindar kotrlja uz klizanje, tada će promjena njegove kinetičke energije biti određena i radom sila trenja. Potonje, za razliku od slučaja kada tijelo klizi po hrapavoj površini bez rotacije, određeno je, u skladu sa (3.14), ukupnim uglom rotacije cilindra, a ne rastojanjem kroz koje se njegova os kretala. .
Zaključak
Dinamika krutog tijela u ovoj fazi koristi se za tijela koja se kreću u kontinuiranom mediju.
U zadatku leta tijela sa tri nosive površine u prisustvu dinamičke asimetrije određuju se uvjeti pod kojima se javljaju sinhronizmi 1:3. S povećanjem ugaone brzine rotacije tijela oko uzdužne ose, čak i na površini raspršivanja, primjetno je slabljenje ovog efekta.
Razvijen je simulacijski program za set problema o dinamici leta protivgradnih projektila. Uz njegovu pomoć napravljene su tablice za uvođenje korekcija uglova ugradnje lansiranja raketa za najbolju kompenzaciju štetnog djelovanja vjetra.
Napravljen je mehanički i matematički model leta bumeranga. Otvoren je laboratorij za navigaciju i upravljanje.
U aerotunelu A-8 razvijen je i implementiran kompleks mehaničke opreme i prateće mjerne opreme za dinamičko ispitivanje modela. Određeni su koeficijenti prigušenja poprečnih vibracija osnosimetričnih pernatih tijela različitih izduženja pri rotaciji oko vlastite ose u pod- i nadzvučnim strujanjima.
Na osnovu numeričkog rješenja problema ravnog kretanja aerodinamičkog klatna (sa nosivom površinom u obliku pravokutne ploče) u nestišljivoj tekućini, uzimajući u obzir dinamiku vrtloga, područja postojanja svih vrsta klatna kretanje, uključujući načine samooscilacije i autorotacije, određuju se. Otvoren je laboratorij nadzvučne aerodinamike.
Institut za kompjuterska istraživanja takođe sprovodi značajna istraživanja dinamike krutog tela.
Ovaj pravac istraživanja instituta vezan je za analizu kretanja krutog tijela uz raširenu upotrebu kompjuterskih metoda.
Kompjuterska istraživanja dinamike krutih tijela pripadaju posebnoj nauci – kompjuterskoj dinamici, koja utvrđuje opšte zakone kretanja sistema uz pomoć različitih numeričkih metoda i algoritama.
U kombinaciji sa analitičkim metodama, napretkom u topologiji, analizi, teoriji stabilnosti i drugim metodama, kompjuterska dinamika se koristi uglavnom u proučavanju integrabilnih problema, posebno dinamičkih problema teorije vrhova. Ovaj pristup vam omogućava da dobijete prilično potpuno razumijevanje pokreta, shvatite svu njegovu raznolikost i vizualno zamislite svaki određeni pokret i njegove karakteristike.
Pored analize integrabilnih situacija, institut je započeo istraživanje slučajeva haotičnog ponašanja u dinamici krutog tijela. Ove studije, koje skoro nikada ranije nisu rađene, oslanjaju se na ekstenzivnu upotrebu kompjuterskog modeliranja visoke preciznosti. Očekuje se da će proučavanje ove oblasti dinamike krutog tijela dati mnogo novih zanimljivih rezultata u budućnosti.
Osim toga, institut provodi istraživanja koristeći metode Poissonove dinamike i geometrije, teorije grupa i Lievih algebri - metoda koje su u velikoj mjeri proizašle iz problema u dinamici krutog tijela.



VPO "DRŽAVNI UNIVERZITET ČEREPOVEC" Fakultet opšte matematike i prirodnih nauka Katedra za opštu fiziku LABORATORIJSKI RAD br. 23 Proveru osnovnog zakona dinamike rotacionog kretanja krutog tela u odnosu na nepokretnu osu izvršili su: student gr. 5SKb-11 Čerepovec, 2009/10 akademska godina. Godina provjere: Assis. Gerasimov R.A. Uvod...

Ovo je problem laserskog hlađenja čvrstih materija. Na sobnoj temperaturi, atomi i molekuli koji čine zrak kreću se u različitim smjerovima brzinom od oko 4000 km/h. Takve atome i molekule je teško proučavati jer prebrzo nestaju iz posmatranja. Snižavanjem temperature možete smanjiti brzinu, ali problem je u tome što pri hlađenju gasovi obično...
Osnovni zakon dinamike može se napisati u drugačijem obliku, poznavajući koncept centra mase sistema:
Tamo je jednadžba kretanja centra mase sistema, jedna od najvažnijih jednačina mehanike. On kaže da se centar mase bilo kog sistema čestica kreće kao da je cijela masa sistema koncentrisana u toj tački i da su na njega primijenjene sve vanjske sile.
Ubrzanje centra mase sistema je potpuno nezavisno od tačaka primene spoljnih sila.
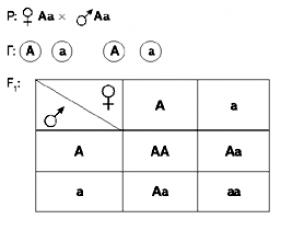
Ako , Tada , Tada i je slučaj zatvorenog sistema u inercijskom referentnom okviru. Dakle, ako se centar mase sistema kreće ravnomjerno i pravolinijski, to znači da se njegov zamah zadržava tokom kretanja.
Primer: homogeni cilindar mase i poluprečnika kotrlja se niz nagnutu ravan stvarajući ugao sa horizontalom bez klizanja. Naći jednačinu kretanja?
| |
Zajedničko rješenje daje vrijednosti parametara
Jednačina kretanja centra mase poklapa se sa osnovnom jednačinom dinamike materijalne tačke i njena je generalizacija na sistem čestica: ubrzanje sistema kao celine proporcionalno je rezultanti svih spoljašnjih sila i obrnuto. proporcionalno masi sistema.
Referentni sistem koji je čvrsto povezan sa centrom mase, koji se translaciono kreće u odnosu na ISO, naziva se sistem centara mase. Njegova posebnost je da je ukupni impuls sistema čestica u njemu uvijek jednak nuli, kao .
Kraj rada -
Ova tema pripada sekciji:
Kinematika translatornog kretanja
Fizičke osnove mehanike.. kinematika translatornog kretanja.. mehaničko kretanje je oblik postojanja..
Ako vam je potreban dodatni materijal na ovu temu, ili niste pronašli ono što ste tražili, preporučujemo da koristite pretragu u našoj bazi radova:
Šta ćemo sa primljenim materijalom:
Ako vam je ovaj materijal bio koristan, možete ga spremiti na svoju stranicu na društvenim mrežama:
| Tweet |
Sve teme u ovoj sekciji:
Mehanički pokret
Materija, kao što je poznato, postoji u dva oblika: u obliku supstance i polja. Prvi tip uključuje atome i molekule od kojih su izgrađena sva tijela. Drugi tip uključuje sve vrste polja: gravitaciju
Prostor i vrijeme
Sva tijela postoje i kreću se u prostoru i vremenu. Ovi koncepti su fundamentalni za sve prirodne nauke. Svako tijelo ima dimenzije, tj. njegov prostorni opseg
Referentni sistem
Da bi se nedvosmisleno odredio položaj tijela u proizvoljnom trenutku, potrebno je odabrati referentni sistem - koordinatni sistem opremljen satom i kruto povezan sa apsolutno krutim tijelom, prema
Kinematske jednadžbe kretanja
Kada se t.M kreće, njegove koordinate se mijenjaju s vremenom, stoga je za specificiranje zakona kretanja potrebno naznačiti vrstu funkcije
Kretanje, elementarno kretanje
Neka se tačka M kreće od A do B duž zakrivljene putanje AB. U početnom trenutku njegov radijus vektor je jednak
Ubrzanje. Normalno i tangencijalno ubrzanje
Kretanje tačke takođe karakteriše ubrzanje – brzina promene brzine. Ako je brzina tačke za proizvoljno vrijeme
Kretanje naprijed
Najjednostavniji tip mehaničkog kretanja krutog tijela je translacijsko kretanje, u kojem se prava linija koja povezuje bilo koje dvije točke tijela kreće s tijelom, ostajući paralelna | its
Zakon inercije
Klasična mehanika se zasniva na tri Newtonova zakona, koje je on formulisao u svom eseju „Matematički principi prirodne filozofije“, objavljenom 1687. Ovi zakoni su bili rezultat genija
Inercijski referentni okvir
Poznato je da je mehaničko kretanje relativno i njegova priroda zavisi od izbora referentnog sistema. Prvi Newtonov zakon ne vrijedi u svim referentnim okvirima. Na primjer, tijela koja leže na glatkoj površini
Težina. Njutnov drugi zakon
Glavni zadatak dinamike je odrediti karakteristike kretanja tijela pod utjecajem sila koje se na njih primjenjuju. Iz iskustva je poznato da pod uticajem sile
Osnovni zakon dinamike materijalne tačke
Jednačina opisuje promjenu kretanja tijela konačnih dimenzija pod utjecajem sile u odsustvu deformacije i ako je
Njutnov treći zakon
Zapažanja i eksperimenti pokazuju da je mehaničko djelovanje jednog tijela na drugo uvijek interakcija. Ako tijelo 2 djeluje na tijelo 1, onda se tijelo 1 nužno suprotstavlja njima
Galilejeve transformacije
Oni omogućavaju određivanje kinematičkih veličina tokom prelaska iz jednog inercijalnog referentnog sistema u drugi. Uzmimo
Galilejev princip relativnosti
Ubrzanje bilo koje tačke u svim referentnim sistemima koji se međusobno kreću pravolinijski i jednoliko na isti način:
Količine konzervacije
Svako tijelo ili sistem tijela je skup materijalnih tačaka ili čestica. Stanje takvog sistema u nekom trenutku u mehanici određuje se specificiranjem koordinata i brzina u
Centar mase
U bilo kom sistemu čestica možete pronaći tačku koja se zove centar mase
Konzervativne snage
Ako u svakoj tački prostora sila djeluje na česticu koja je tamo smještena, za česticu se kaže da se nalazi u polju sila, na primjer, u polju gravitacije, gravitacije, Kulonove i drugih sila. Polje
Centralne snage
Svako polje sile je uzrokovano djelovanjem određenog tijela ili sistema tijela. Sila koja djeluje na česticu u ovom polju je oko
Potencijalna energija čestice u polju sila
Činjenica da rad konzervativne sile (za stacionarno polje) zavisi samo od početne i krajnje pozicije čestice u polju omogućava nam da uvedemo važan fizički koncept potencijala
Odnos potencijalne energije i sile za konzervativno polje
Interakcija čestice sa okolnim tijelima može se opisati na dva načina: korištenjem koncepta sile ili korištenjem koncepta potencijalne energije. Prva metoda je opštija, jer važi i za sile
Kinetička energija čestice u polju sila
Neka se čestica mase kreće u sili
Ukupna mehanička energija čestice
Poznato je da je prirast kinetičke energije čestice pri kretanju u polju sila jednak elementarnom radu svih sila koje djeluju na česticu:
Zakon održanja mehaničke energije čestica
Iz izraza slijedi da se u stacionarnom polju konzervativnih sila ukupna mehanička energija čestice može promijeniti
Kinematika
Možete rotirati svoje tijelo pod određenim uglom
Moment čestice. Trenutak snage
Osim energije i zamaha, postoji još jedna fizička veličina s kojom je povezan zakon održanja - to je ugaoni moment. Ugaoni moment čestice
Moment impulsa i moment sile oko ose
Uzmimo proizvoljnu fiksnu osu u referentnom sistemu koji nas zanima
Zakon održanja ugaonog momenta sistema
Razmotrimo sistem koji se sastoji od dvije čestice koje međusobno djeluju, na koje također djeluju vanjske sile i
Dakle, ugaoni moment zatvorenog sistema čestica ostaje konstantan i ne mijenja se s vremenom
Ovo vrijedi za bilo koju tačku u inercijskom referentnom sistemu: . Momenti impulsa pojedinih delova sistema m
Moment inercije krutog tijela
Zamislite čvrsto tijelo koje može
Jednačina dinamike rotacije krutog tijela
Jednadžba za dinamiku rotacije krutog tijela može se dobiti pisanjem jednadžbe momenata za kruto tijelo koje rotira oko proizvoljne ose
Kinetička energija rotirajućeg tijela
Razmotrimo apsolutno kruto tijelo koje rotira oko fiksne ose koja prolazi kroz njega. Hajde da ga razbijemo na čestice male zapremine i mase
Rad rotacije krutog tijela
Ako se tijelo rotira silom
Centrifugalna sila inercije
Razmotrimo disk koji se rotira zajedno sa loptom na oprugi navučenoj na žbicu, slika 5.3. Lopta se nalazi
Coriolisova sila
Kada se tijelo kreće u odnosu na rotirajući CO, osim toga, pojavljuje se još jedna sila - Coriolisova sila ili Coriolisova sila
Male fluktuacije
Razmotrimo mehanički sistem čiji se položaj može odrediti pomoću jedne veličine, kao što je x. U ovom slučaju se kaže da sistem ima jedan stepen slobode
Harmonične vibracije
Jednadžba 2. Newtonovog zakona u odsustvu sila trenja za kvazielastičnu silu oblika ima oblik:
Matematičko klatno
Ovo je materijalna tačka okačena na neraširivoj niti dužine, koja osciluje u vertikalnoj ravni
Fizičko klatno
Ovo je čvrsto tijelo koje vibrira oko fiksne ose povezane s tijelom. Osa je okomita na sliku i
Prigušene oscilacije
U realnom oscilatornom sistemu postoje sile otpora čije djelovanje dovodi do smanjenja potencijalne energije sistema, a oscilacije će u najjednostavnijem slučaju biti prigušene
Samooscilacije
Kod prigušenih oscilacija energija sistema se postepeno smanjuje i oscilacije prestaju. Da bi ih učinili neprigušenim, potrebno je u određenim trenucima dopuniti energiju sistema izvana
Prisilne vibracije
Ako je oscilatorni sistem, pored sila otpora, podložan djelovanju vanjske periodične sile koja se mijenja po harmonijskom zakonu
Rezonancija
Kriva zavisnosti amplitude prinudnih oscilacija od dovodi do toga da pri nekom specifičnom za dati sistem
Širenje talasa u elastičnom mediju
Ako se izvor oscilovanja postavi na bilo koje mjesto u elastičnom mediju (čvrstom, tekućem, plinovitom), tada će se zbog interakcije između čestica oscilacija širiti u mediju od čestice do sata.
Jednadžba ravnih i sfernih valova
Talasna jednadžba izražava ovisnost pomaka oscilirajuće čestice od njenih koordinata,
Talasna jednadžba
Talasna jednačina je rješenje diferencijalne jednadžbe koja se zove valna jednačina. Da bismo to ustanovili, nalazimo druge parcijalne izvode s obzirom na vrijeme i koordinate iz jednačine
U bilo kom sistemu materijalnih tačaka, a samim tim i u bilo kom sistemu tela, postoji jedna izuzetna tačka C, koja se zove centar mase ili centar inercije sistema. Njegov položaj je određen radijus vektorom r c:
Za centar mase je tačna sljedeća tvrdnja: Kada se bilo koji sistem čestica kreće, njegovo težište se pomiče kao da je čitava masa sistema koncentrisana u ovoj tački i sve vanjski sile koje deluju na sistem. Prema formi jednadžba kretanja centra mase poklapa se sa drugim Newtonovim zakonom:
gdje je ubrzanje centra mase.
Jednadžba dinamike rotacijskog kretanja
At rotaciono kretanje krutog tela Analog drugog Newtonovog zakona je osnovna jednadžba za dinamiku rotacionog kretanja, koji izgleda ovako:
Gdje e- ugaono ubrzanje, M- ukupan moment sila u odnosu na osu rotacije. Ako se moment inercije tijela promijeni tokom kretanja, onda se ovaj zakon mora primijeniti u sljedećem obliku:
gdje je ugaoni moment krutog tijela.
Svako kretanje krutog tijela može se predstaviti kao superpozicija dva glavna tipa kretanja – translacijskog i rotacijskog. Na primjer, kotrljanje lopte može se smatrati kretanjem s ubrzanjem jednakom ubrzanju centra mase i rotacijom oko ose koja prolazi kroz centar mase. Svaki pokret poštuje, kao što je prikazano u tabeli 5, odgovarajući zakon.
Zakoni dinamike u neinercijalnim referentnim sistemima.
Inercijske sile
Referentni okviri koji se kreću ubrzanjem u odnosu na inercijalne okvire nazivaju se neinercijalni (NISO), a zakoni dinamike o kojima smo gore govorili nisu zadovoljeni u njima: drugi Newtonov zakon, jednačina kretanja centra mase, jednačina dinamike rotacijskog kretanja. Međutim, mogu se sačuvati i za neinercijalne sisteme ako pored uobičajenih interakcijskih sila F uvesti više “sila” posebne prirode Fin, zvao sile inercije. Njihovo uvođenje je zbog ubrzanja kretanja neinercijalnog referentnog okvira u odnosu na inercijski.
Zakoni dinamike Tabela 5
| Fizička situacija | Važeći zakoni |
| Pravolinijsko kretanje materijalne tačke, translatorno kretanje krutog tijela | Njutnov drugi zakon |
| Kretanje materijalne tačke duž kružnice ili druge zakrivljene putanje | Njutnov drugi zakon |
| Rotacija krutog tijela oko fiksne ose | Osnovni zakon dinamike rotacionog kretanja |
| Složeno kretanje krutog tijela | Jednadžba gibanja centra mase i jednadžba dinamike rotacionog kretanja |
U NISO, zakoni dinamike će imati oblik:
Newtonov drugi zakon +;
jednadžba kretanja centra mase + ;
jednadžba dinamike rotacijskog kretanja + .
Postoje dvije glavne vrste neinercijalnih sistema. Označimo simbolom TO inercijalni referentni sistem, i - neinercijalni.
1. kreće relativno TO sa konstantnim ubrzanjem. U ovom slučaju treba uvesti u jednačine dinamike sila inercije, jednako = - ma c. Točkom primjene ove sile smatra se centar mase.
Dot WITH, čiji je položaj određen radijus vektorom:
pozvao centar mase sistemi materijalnih tačaka. Evo m i- težina i th particle; r i- radijus vektor koji specificira poziciju ove čestice; - ukupna masa sistema. (Imajte na umu da se u uniformnom polju gravitacije centar mase poklapa sa centrom gravitacije sistema.)
Nakon diferenciranja r C u vremenu nalazimo brzinu centra mase:
Gdje V i- brzina i-ta materijalna tačka, str i- njen impuls, P – impuls sistema materijalnih tačaka. Iz (2.18) slijedi da je ukupni impuls sistema
P = m V C, (2.19)
Iz (2.19) i (2.16) dobijamo jednačinu kretanja centra mase:
(A C– ubrzanje centra mase). Dakle, iz jednadžbe.
slijedi da se centar mase kreće na isti način kao što bi se kretala materijalna tačka s masom jednakom masi sistema pod djelovanjem rezultante svih vanjskih sila primijenjenih na tijela sistema. Za zatvoreni sistem i C = 0. To znači da centar mase zatvorenog sistema kreće se pravolinijski i jednoliko ili miruje.
Referentni sistem u odnosu na koji centar mase miruje naziva se sistem centra mase(skraćeno ts- sistem). Ovaj sistem je inercijalan.
Kontrolna pitanja
1. U kojim referentnim okvirima vrijede Newtonovi zakoni?
2. Koje formulacije drugog Newtonovog zakona znate?
3. Kolika je težina tijela koje slobodno pada?
4. Koliki je predznak skalarnog proizvoda sile trenja i brzine tijela?
5. Koliki je impuls sistema materijalnih tačaka u sistemu centara mase?
6. Kolika je akceleracija centra mase tijela koje ima masu m a pod uticajem sila?
1. Metak probija dvije susjedne kutije s tekućinama: prvo kutiju s glicerinom, zatim istu kutiju s vodom. Kako će se promijeniti konačna brzina metka ako se kutije zamijene? Druge sile koje djeluju na metak osim otpora tekućini F = – r V , zanemarivanje.
2. Kretanje materijalne tačke je dato jednačinama x = a t 3 , y= b t.
3. Brzina materijalne tačke data je jednačinama u x = A ∙ sinw t,u y = A∙ cosw t. Da li se sila koja djeluje na tačku mijenja: a) po veličini; b) u pravcu?
4. Kuglica koja visi o dugoj niti l, nakon što se horizontalni guranje podigne na visinu H bez napuštanja kruga. Može li njegova brzina biti jednaka nuli: a) kada H< l b) kod H>l?
5. Dva tijela sa masama T 1 > m 2 pada sa iste visine. Sile otpora se smatraju konstantnim i identičnim za oba tijela. Uporedite vrijeme pada tijela.
6. Dvije identične šipke povezane navojem kreću se duž horizontalne ravni pod djelovanjem horizontalne sile F . Da li sila zatezanja konca zavisi od: a) mase šipki; b) o koeficijentu trenja između šipki i ravni?
7. Blok mase m 1 = 1 kg leži na bloku mase m 2 = 2 kg. Horizontalna sila je počela djelovati na donji blok, povećavajući se proporcionalno vremenu, njegov modul F= 3t(F– u N, t- u c). U kom trenutku će gornji blok početi da klizi? Koeficijent trenja između šipki je m = 0,1, trenje između donje šipke i oslonca je zanemarivo. Prihvati g= 10 m/s 2.
8. Dvije kuglice a i b, obješene na niti u zajedničkoj tački 0, kreću se jednoliko duž kružnih putanja koje leže u istoj horizontalnoj ravni. Uporedite njihove ugaone brzine.
9. Konusni lijevak rotira konstantnom kutnom brzinom w. Unutar lijevka na zidu leži tijelo koje može slobodno kliziti duž tvornice konusa. Tokom rotacije, tijelo je u ravnoteži u odnosu na zid. Da li je ova ravnoteža stabilna ili nestabilna?
Poglavlje 3
Rad i energija
Jednačina kretanja centra mase u vektorskom obliku
Položaj i kretanje aviona u letu određuju se u odnosu na površinu Zemlje. Stoga se kao glavni referentni sistem uzima geocentrični neinercijalni koordinatni sistem koji je povezan sa Zemljom i koji sa njom vrši dnevnu rotaciju.
rotacija sa ugaonom brzinom co3 (zemaljski referentni sistem).
Kretanje centra mase aviona opisuje se dinamikom
jednadžba (1.7), koja nakon zamjene FBIi = RA + mgr poprima oblik
m^^P + RA + mgr + F’ + F*, (1.32)
gdje je 1/k vektor brzine centra mase aviona u odnosu na
konkretno Zemlja i gr je vektor gravitacionog ubrzanja.
Sile prijenosa i Coriolisove inercije povezane s rotacijom Zemlje određene su izrazima poznatim iz teorijske mehanike
Fe - - mWe == - m
KK = - m#K = - 2m(to3 x VK), . (1.33)
gde je r vektor radijusa povučen od početka geocentričnog referentnog sistema 0° do centra mase vazduhoplova; Mi i I7K su prenosiva i Koriolisova ubrzanja centra mase, uzrokovana rotacijom odabranog geocentričnog referentnog sistema u odnosu na inercijski. ‘ .., .
Pošto referentne tabele obično daju vrednosti ubrzanja usled gravitacije, uzimajući u obzir prenosnu silu inercije u zavisnosti od visine, onda je na desnoj strani jednačine (1.32) moguće
geometrijski zbir sila gravitacionog privlačenja. mgr i prenosiva inercijalna sila F1 zamjenjuju se gravitacijom G:
G = mgt + Fe - mg. (1-34)
U (1.34) g je vektor rezultirajućeg gravitacionog ubrzanja i centrifugalne sile.
Zapisujemo vektorsku jednačinu (1.32) uzimajući u obzir (1.34) u obliku
t^g=? + ^ + ®1+?k — O-35)
Kao što je navedeno u § 1.1, u praktičnoj primeni vektorska jednačina kretanja se projektuje na osu pravougaonog koordinatnog sistema. Izbor koordinatnog sistema za sastavljanje diferencijalnih jednačina kretanja za centar mase aviona određen je problemom istraživanja. Prilikom proučavanja putanja obično se koriste ose putanje. U isto vrijeme, pogodnije je razmatrati probleme stabilnosti i upravljivosti u spregnutom koordinatnom sistemu.
Jednačine kretanja centra mase u koordinatnom sistemu trajektorije
Sistem dinamičkih jednačina kretanja centra mase aviona (translaciono kretanje) poprimiće najjednostavniji i najpogodniji oblik ako se vektorska jednačina (1.35) projektuje na osu koordinatnog sistema trajektorije.
Primenjujući formule (1.9) za projektovanje leve strane jednačine (1.35) i uzimajući u obzir da je 1/*„ = VI:, Vm = Vzi: =0, dobijamo
tUk = Rhi G Xxk ~b GXK ~b P*k‘> tyg^Uk - P!,k g Ui; b G,;K - F(1.36) - tyugUK - PZK “b ~ b GZK f F*k,
gdje (oun, sogk - projekcije na osi putanje vektora ugaone brzine
rast (o rotaciji koordinatnog sistema putanje u odnosu na Zemlju; desna strana pokazuje projekcije odgovarajućih sila na osi trajektorije.
Da biste napisali ove jednačine u proširenom obliku, trebate
naći projekcije ugaone brzine soka, kao i projekcije Corioli-
zbog sile inercije FK na osi trajektorije. Projekcije vanjskih sila i potiska na ove ose definirane su u § 1.6.
Ugaona brzina co„ može se predstaviti kao zbir prenosivih
ugaona brzina abbr normalan sistem 0XgYgZg u sistemu od-
broji O^X^YqZq i ugaonu brzinu rotacije sistema brzina u odnosu na normalu:
san = coKr -|- coKg. (1.37)
Prijenosna kutna brzina abbr, zauzvrat, može biti predstavljena sumom ugaonih brzina:
Shkr -Ya-f-f, (1.38)
gdje je K ugaona brzina rotacije meridionalne ravni,
Ugaona brzina coKg se takođe može predstaviti kao
zbir ugaone brzine Fg oko ose OYg i ugaone brzine 0 oko ose OZg (vidi sliku 1.5):
Korišćenje tabele I (vidi dodatak) kosinusa smjera, nalazimo projekcije vektora na osu OY„ i OZK sistema putanja
co^j, = I (sin e cos 0 - cos F sin Y sin 0) F sin Y sin 0 + !F cos 0;
sogk = I, cos φ sin V - φ cos V ~f - 0, (1-40)
koji će nakon zamjene izraza (1.21) kao rezultat jednostavnih transformacija imati oblik
gj,(K = ¥ cos 0 V sin 4r cos20 tan f/(/?z - f I);
co2K = 0 - I cos Q/(R3 + I). (1.41)
Pronađimo sada projekcije Coriolisove inercijalne sile na osi traga. Vektor Coriolisove sile inercije određen je formulom poznatom iz mehanike
FK ~ - mwK = - 2t(i3 x Kk) (1-42)
i okomito (03 i Uk.
Projekcije Coriolisove inercijalne sile na osu sistema putanje izražene su formulama
Kk = 0; FyK = 2ma>aVR cos f cos
F*k = 2mcoaVK (sin F cos 0 - cos F sin ‘P sin 0).
Zamjena u (1.36) izraza za projekcije ugaonih brzina definisanih formulama (1.41), projekcije potiska, aerodinamičke sile, gravitacije (vidi formule (1.27) i (1.28), kao i (1.30)) i projekcije Coriolisove sile inercije, izražene formulama (1.43), dobijamo sistem dinamičkih jednadžbi kretanja centra mase aviona u odnosu na sferno rotirajuću Zemlju u projekcijama na osu koordinatnog sistema putanje (u odsustvu vetra uk = V, ¥ = phi):
mV - P cos (a + f,) cos p - Xa - mg sin 0; (1.44)
mVQ = P = pha
p1t = R fsln (" + COS Ua + cos (o - f Fâ) Staljin ua1 +
Ya cos y a - Zu sin Y0) = nya cos y a - nzU sin ya nzk = -^(p fR) sin p cos yJ h + Y a sin ya + Za cos = tiya sin Yn + "go COS Yo-
U (1.49) i (1.50) aerodinamičke sile su definirane u sustavu brzina koordinatnih osa. .
‘ Podijeleći lijevu i desnu stranu jednadžbe (1.44) ... (1.46) sa O = mg, dobijamo dinamičke jednadžbe gibanja centra mase pod preopterećenjima
V ?= pHa - sin 0;
Jr e = tlya COS Yu - “za Sin Yu - COS 0 |-
f - cos ph sin ¥ (/?z + //)’. (1.51)
——— - í = nya sin Yu - “70 cos Ya H — - C0B to (simp cos 0 -
Cos f cos ¥ sin 0) - VI cosE0 sin ¥ tg
„Kada se razmatraju posebni slučajevi kretanja aviona, izrazi za projekcije preopterećenja su značajno pojednostavljeni.
Za]) let bez klizanja (ft == O, Za = 0) sa malim napadnim uglovima, kada možemo uzeti sin (a + phR) « a + fR, cos (os + + Fr)» 1, formule (1.49 ) i (1.50) će poprimiti oblik
R-Ha. .. R(a + Fr) + Co. ha~ mg ■’ pch°~ Traži *
pga = 0 (1,52)
i, bez vjetra, "‘ 1' ■
“zhk ~ “zsa” pu* =.■“№COS Yu’.. “Li = “j/aSin Yu - (15)
U projekcijama na povezane ose, vektor preopterećenja može biti predstavljen komponentama px, pu i nz, koje se nazivaju uzdužno, normalno i poprečno preopterećenje, respektivno. Koristeći tablicu kosinusa smjera, dobijamo
Px = pha COS a COS P + pia sin o - nzu cos os Sin P; 4
pu - - pha sin a cos P -)- pua cos a + pga sin a sin P; (1-54) "g = nxa Si" P + "ha cos P-
§ 1.8. DINAMIČKE JEDNAČINE KRETANJA AVIONA U ODNOSU NA CENTAR MASA
Pogodno je proučavati kretanje aviona u odnosu na centar mase (rotacijski ili ugaoni) ako koristimo dinamičke jednačine u projekcijama na ose pridruženog koordinatnog sistema 0XYZ. Prilikom proučavanja ugaonog kretanja samog sebe
U letu, baš kao i pri određivanju putanja centra mase, kao referentni sistem se koristi neinercijalni sistem povezan sa Zemljom.
Projektovanjem vektorske jednačine (1.8) na osu pridruženog koordinatnog sistema i korišćenjem formula (1.9) za izračunavanje projekcija vremenskih derivata vektora ugaonog momenta aviona, dobijamo sistem skalarnih jednačina kretanja aviona u odnosu na centar mase (rotacijsko ili kutno kretanje)
*§.- + coyKz-a>zKy = MRx)
J - agKx bzxKg = Mru’, (1,55)
Rff - + LxKy - b)1/Kx = Mrg,
gdje su Kx, Ky, Kr projekcije vektora ugaonog momenta zrakoplova na pridružene koordinatne ose; (oh, yu, (oz - projekcije vektora ugaone brzine aviona u odnosu na Zemlju na iste ose; MRx, MRu, MRz - projekcije rezultujućeg momenta aerodinamičkih sila i potiska u odnosu na centar mase na istim osema Treba imati na umu da je moment masenih sila (sile gravitacije, centrifugalne i Coriolisove sile inercije) oko centra mase aviona jednak nuli.
Ugaona brzina aviona u odnosu na Zemlju je zbir vektora ugaone brzine aviona u odnosu na normalu
koordinatni sistem i ugaona brzina (o rotaciji normalnog koordinatnog sistema u odnosu na Zemlju zbog zakrivljenosti Zemljine površine. Za stvarne uslove leta aviona, ovo drugo
komponenta yr je mala i može se zanemariti.
Projekcije kinetičkog momenta K na proizvoljne pokretne dijelove! ose se u teorijskoj mehanici zapisuju kao /’V-;
Kh JH^H ‘ /xytoy /hg(0g)
gdje su /zh, Jy, Jz aksijalni, a 7*„, Jxz, uJyZ su centrifugalni momenti inercije, koji se određuju formulama:
Jx = J (ug + z) dm Jy - J (Xí - f z-) dm)
Jz = j (Xí + Uʺ) dm; Jay = jxy dm
Jxi = j xz dm) Jyz = j t/z dm.
Momenti inercije aviona sa primetno promenljivom masom tokom leta su funkcije vremena.
Pošto je glavna ravan OXY pridruženog koordinatnog sistema ravan simetrije aviona, tada su u pridruženim osama centrifugalni momenti inercije koji sadrže z koordinate jednaki nuli: Jxz - Juz - - 0.
Uzimajući u obzir ovo pojednostavljenje, koristeći izraze (1.56), zapisujemo jednačine (1.55) u obliku
Jx^x ^xy®y i g ^ y) ^ xy^x^y == px)
Ju®U ^hu®h (/ž ‘ *^g) ®žV)g Jx^z == ^Ry’i
Jg b (^y ^x) ^[>x^[)y Jxy (Š* Wp) = Aí rg.
O izrazima za projekcije rezultujućeg momenta MRx, MRy i MRz detaljnije će biti reči u drugom delu knjige kada se analizira ugaono kretanje aviona.