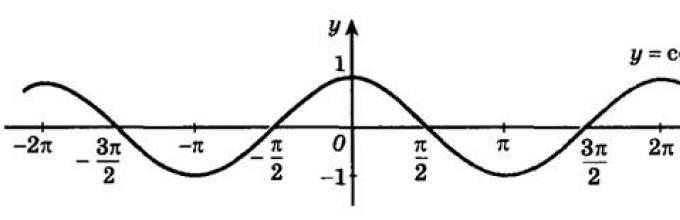
Trigonometrijske funkcije numeričkih i kutnih argumenata. Formule redukcije Izračunajte izraz trigona numeričkog argumenta

Trigonometrijske funkcije numeričkog argumenta.

Trigonometrijske funkcije numeričkog argumentat su funkcije forme y= cos t,
y= sin t, y= tg t, y= ctg t.

Koristeći ove formule, preko poznate vrijednosti jedne trigonometrijske funkcije, možete pronaći nepoznate vrijednosti drugih trigonometrijskih funkcija.

Objašnjenja.

1) Uzmite formulu cos 2 t + sin 2 t = 1 i upotrijebite je za izvođenje nove formule.

Da biste to učinili, podijelite obje strane formule sa cos 2 t (za t ≠ 0, to jest, t ≠ π/2 + π k). dakle:

cos 2 t sin 2 t 1
--- + --- = ---
cos 2 t cos 2 t cos 2 t

Prvi član je jednak 1. Znamo da je omjer sinusa i konisa tangentan, što znači da je drugi član jednak tg 2 t. Kao rezultat, dobijamo novu (i vama već poznatu) formulu:

2) Sada podijelite cos 2 t + sin 2 t = 1 sa sin 2 t (za t ≠ π k):

cos 2 t sin 2 t 1
--- + --- = ---, gdje je t ≠ π k + π k, k– cijeli broj
sin 2 t sin 2 t sin 2 t

Omjer kosinusa i sinusa je kotangens. znači:

Poznavajući osnovne principe matematike i naučivši osnovne formule trigonometrije, lako možete sami izvesti većinu ostalih trigonometrijskih identiteta. A ovo je još bolje nego da ih samo naučite napamet: ono što naučite napamet brzo se zaboravlja, ali ono što shvatite pamti se dugo, ako ne i zauvijek. Na primjer, nije potrebno zapamtiti koliko je jednak zbir jedinice i kvadrata tangente. Ako ste zaboravili, možete se lako sjetiti ako znate najjednostavniju stvar: tangenta je omjer sinusa i kosinusa. Osim toga, primijenite jednostavno pravilo zbrajanja razlomaka s različiti imenioci– i dobijete rezultat:

sin 2 t 1 sin 2 t cos 2 t + sin 2 t 1
1 + tg 2 t = 1 + --- = - + --- = ------ = ---
cos 2 t 1 cos 2 t cos 2 t cos 2 t

Na isti način možete lako pronaći zbir jedan i kvadrat kotangensa, kao i mnoge druge identitete.

Trigonometrijske funkcije kutnog argumenta.

U funkcijamaat = cost, at = grijeht, at = tgt, at = ctgt varijablat može biti više od samo numeričkog argumenta. Može se smatrati i mjerom ugla - to jest ugaonim argumentom.

Korišćenjem brojčani krug i koordinatnih sistema, možete lako pronaći sinus, kosinus, tangent, kotangens bilo kojeg ugla. Da biste to učinili, moraju se ispuniti dvije stvari važnih uslova:
1) vrh ugla mora biti centar kružnice, koji je ujedno i centar koordinatne ose;

2) jedna od strana ugla mora biti snop pozitivne ose x.

U ovom slučaju, ordinata tačke u kojoj se sijeku kružnica i druga strana ugla je sinus ovog ugla, a apscisa ove tačke je kosinus ovog ugla.

Objašnjenje. Nacrtajmo ugao čija je jedna strana pozitivna zraka ose x, a druga strana izlazi iz početka koordinatne ose (i iz centra kružnice) pod uglom od 30º (vidi sliku). Tada tačka preseka druge strane sa kružnicom odgovara π/6. Znamo ordinatu i apscisu ove tačke. Oni su također kosinus i sinus našeg ugla:

√3 1
--; --
2 2

A znajući sinus i kosinus ugla, lako možete pronaći njegovu tangentu i kotangens.

Dakle, brojevni krug, koji se nalazi u koordinatnom sistemu, je zgodan način za pronalaženje sinusa, kosinusa, tangenta ili kotangensa ugla.

Ali postoji lakši način. Ne morate crtati krug i koordinatni sistem. Možete koristiti jednostavne i praktične formule:

Primjer: pronađite sinus i kosinus ugla jednakog 60º.

Rješenje:

π 60 π √3
sin 60º = sin --- = sin -- = --
180 3 2

π 1
cos 60º = cos -- = -
3 2

Objašnjenje: otkrili smo da sinus i kosinus ugla od 60º odgovaraju vrijednostima tačke na kružnici π/3. Zatim jednostavno pronađemo vrijednosti ove točke u tablici - i tako riješimo naš primjer. Tabela sinusa i kosinusa glavnih tačaka brojevnog kruga nalazi se u prethodnom dijelu i na stranici „Tabele“.

U ovom poglavlju ćemo uvesti trigonometrijske funkcije numeričkog argumenta. Mnoga pitanja iz matematike, mehanike, fizike i drugih nauka dovode do trigonometrijskih funkcija ne samo ugla (luka), već i argumenata sasvim druge prirode (dužine, vremena, temperature, itd.). Do sada se argument trigonometrijske funkcije shvatao kao ugao meren u stepenima ili radijanima. Sada ćemo generalizovati koncepte sinusa, kosinusa, tangente, kotangensa, sekansa i kosekansa tako što ćemo ih uvesti kao funkcije numeričkog argumenta.

Definicija. Trigonometrijske funkcije numeričkog argumenta su istoimenovane trigonometrijske funkcije ugla jednakog radijanima.

Objasnimo ovu definiciju konkretnim primjerima.

Primjer 1. Izračunajmo vrijednost. Ovdje mislimo na apstraktno iracionalan broj. Prema definiciji. Dakle, .

Primjer 2. Izračunajmo vrijednost. Ovdje pod 1,5 podrazumijevamo apstraktni broj. Kako je definisano (vidi Dodatak II).

Primjer 3. Izračunajte vrijednost Dobijamo isto kao gore (vidi Dodatak II).

Dakle, u budućnosti ćemo pod argumentom trigonometrijskih funkcija podrazumijevati ugao (luk) ili samo broj, ovisno o problemu koji rješavamo. A u nekim slučajevima, argument može biti veličina koja ima drugu dimenziju, na primjer vrijeme, itd. Nazivajući argument uglom (lukom), možemo pod njim podrazumijevati broj kojim se mjeri u radijanima.

Definicija 1: numerička funkcija, dato formulom y=sin x se naziva sinus.

Ova kriva se zove - sinusni talas.

Svojstva funkcije y=sin x

2. Raspon vrijednosti funkcije: E(y)=[-1; 1]

3. Paritetna funkcija:

y=sin x – neparan,.

4. Periodičnost: sin(x+2πn)=sin x, gdje je n cijeli broj.

Ova funkcija poprima iste vrijednosti nakon određenog perioda. Ovo svojstvo funkcije se zove frekvencija. Interval je period funkcije.

Za funkciju y=sin x period je 2π.

Funkcija y=sin x je periodična, sa periodom T=2πn, n je cijeli broj.

Najmanji pozitivni period je T=2π.

Matematički, ovo se može napisati na sljedeći način: sin(x+2πn)=sin x, gdje je n cijeli broj.

Definicija 2: Numerička funkcija data formulom y=cosx naziva se kosinus.

Svojstva funkcije y=cos x

1. Domen funkcije: D(y)=R

2. Područje vrijednosti funkcije: E(y)=[-1;1]

3. Paritetna funkcija:

y=cos x – paran.

4. Periodičnost: cos(x+2πn)=cos x, gdje je n cijeli broj.

Funkcija y=cos x je periodična, sa periodom T=2π.

Definicija 3: Numerička funkcija data formulom y=tan x naziva se tangenta.

Svojstva funkcije y=tg x

1. Domen funkcije: D(y) - sve realni brojevi, osim π/2+πk, k je cijeli broj. Jer u ovim tačkama tangenta nije definisana.

3. Paritetna funkcija:

y=tg x – neparan.

4. Periodičnost: tg(x+πk)=tg x, gdje je k cijeli broj.

Funkcija y=tg x je periodična sa periodom π.

definicija 4: Numerička funkcija data formulom y=ctg x naziva se kotangens.

Svojstva funkcije y=ctg x

1. Domen definicije funkcije: D(y) - svi realni brojevi osim πk, k je cijeli broj. Zato što u ovim tačkama kotangens nije definisan.

2. Opseg funkcije: E(y)=R.

Nazad napred

Pažnja! Pregledi slajdova služe samo u informativne svrhe i možda ne predstavljaju sve karakteristike prezentacije. Ako ste zainteresovani za ovaj rad, preuzmite punu verziju.

Ciljevi lekcije:

1. Razvoj vještina i vještina primjene trigonometrijske formule da pojednostavi trigonometrijske izraze.
2. Implementacija principa aktivističkog pristupa u nastavi učenika, razvijanje komunikacijskih vještina i tolerancije učenika, sposobnost slušanja i slušanja drugih i izražavanja mišljenja.
3. Povećanje interesovanja učenika za matematiku.

Vrsta lekcije: obuku.

Vrsta lekcije: lekcija o vještinama i sposobnostima.

Forma studija: grupa

Vrsta grupa: grupa sjedi zajedno. Učenici različitog nivoa osposobljenosti, svesti o datom predmetu, kompatibilni učenici, što im omogućava da se međusobno dopunjuju i obogaćuju.

Oprema: ploča; kreda; tablica "Trigonometar"; listovi ruta; kartice sa slovima (A, B, C.) za ispunjavanje testa; tablice s imenima posade; zapisnici; tabele sa nazivima etapa putovanja; magneti, multimedijalni kompleks.

Tokom nastave

Učenici sjede u grupama: 4 grupe od 5-6 osoba. Svaka grupa je posada automobila čiji nazivi odgovaraju nazivima trigonometrijskih funkcija, predvođeni volanom. Svaka posada dobija list rute i određuje se cilj: da zadatu rutu završi uspješno, bez grešaka. Lekciju prati prezentacija.

I. Organizacioni momenat.

Nastavnik saopštava temu časa, svrhu časa, tok časa, plan rada grupa, ulogu kormilara.

Uvodna riječ nastavnika:

– Momci! Zapišite broj i temu lekcije: "Trigonometrijske funkcije brojčanog argumenta."

Danas ćemo na času naučiti:

1. Izračunati vrijednosti trigonometrijskih funkcija;
2. Pojednostavite trigonometrijski izrazi.

Da biste to uradili morate znati:

1. Definicije trigonometrijskih funkcija
2. Trigonometrijske relacije (formule).

Odavno se zna da je jedna glava dobra, a dvije bolje, pa se danas radi u grupama. Takođe je poznato da će onaj ko hoda savladati put. Ali živimo u doba brzine i vrijeme je dragocjeno, što znači da možemo reći i ovo: „Put će savladati oni koji voze“, pa će danas naš čas biti održan u formi igre „Matematički reli“. Svaka grupa je posada vozila, koju vodi volan.

Svrha igre:

• uspješno završiti rutu za svaku posadu;
• identifikuju šampione u reliju.

Ime posade odgovara marki automobila koji vozite.

Predstavljaju se posade i njihovi kormilari:

• Posada – “sinus”
• Posada – “kosinus”
• Posada - "tangenta"
• Posada – “kotangens”

Moto trke: "Požuri polako!"

Morate trčati kroz "matematički teren" sa mnogo prepreka.

Svakoj posadi su izdate rute. Posade koje poznaju definicije i trigonometrijske formule moći će savladati prepreke.

Tokom trčanja, svaki kormilar vodi posadu, pomažući i procjenjujući doprinos svakog člana posade u savladavanju rute u obliku "za" i "protiv" u zapisniku. Za svaki tačan odgovor grupa dobija “+” i netačan odgovor “-”.

Morate savladati sljedeće faze putovanja:

Faza I. SDA (saobraćajna pravila).
Faza II. Tehnički pregled.
Faza III. Kros trka.
Faza IV. Iznenadno zaustavljanje je nesreća.
V faza. Stani.
Faza VI. Završi.
VII faza. Rezultati.

I tako krećemo!

Faza I. SDA (saobraćajna pravila).

1) U svakoj posadi, kormilar dijele karte sa teorijskim pitanjima svakom članu posade:

1. Objasnite definiciju sinusa od t i njegovih znakova po četvrtinama.
2. Objasnite definiciju kosinusa broja t i njegovih znakova po četvrtinama.
3. Imenujte najmanji i najveća vrijednost sin t i cos t.
4. Objasniti definiciju tangente broja t i njegovih znakova po četvrtinama.
5. Objasniti definiciju kotangensa broja t i njegovih znakova po četvrtinama.
6. Recite nam kako pronaći vrijednost sin t funkcije iz poznatog broja t.

2) Prikupite „razbacane“ formule. Na tajnoj ploči nalazi se stol (vidi dolje). Posada mora uskladiti formule. Svaki tim zapisuje odgovor na tabli u obliku reda odgovarajućih slova (u parovima).

A	tg 2 t + 1	e	1
V	tg t	i	cos t / sin t, t ≠ k, kZ.
d	sin 2 t + cos 2 t	I	1/ sin 2 t, t ≠ k, kZ.
e	ctg t	To	1,t ≠ k / 2, kZ.
h	1 + ctg 2 t	G	sin t /cos t, t ≠ /2 + k, kZ.
th	tg t ∙ctg t	b	1/ cos 2 t, t ≠ /2 + k, kZ.

odgovor: ab, vg, de, jež, zi, yk.

Faza II. Tehnički pregled.

Usmeni rad: test.

Na tajnoj tabli je napisano: zadatak: pojednostaviti izraz.

Opcije odgovora su ispisane pored njih. Ekipe utvrđuju tačne odgovore za 1 minut. i pokupite odgovarajući skup slova.

№	Izraz	Opcije odgovora
		A	IN	WITH
1.	1 – cos 2 t	cos 2 t	- sin 2 t	sin 2 t
2.	sin 2 t – 1	cos 2 t	- cos 2 t	2 cos 2 t
3.	(cos t – 1)(1+ cos t)	-sin 2 t	(1+ cos t) 2	(cos t – 1) 2

Odgovor: C V A.

Faza III. Kros trka.

Posada ima 3 minuta za sastanak na kojem se odlučuje o zadatku, a zatim predstavnici posade pišu odluku na tabli. Kada predstavnici posade završe sa zapisivanjem rješenja prvog zadatka, svi učenici (zajedno sa nastavnikom) provjeravaju ispravnost i racionalnost rješenja i zapisuju ih u bilježnicu. Kormilar ocjenjuje doprinos svakog člana posade koristeći znakove “+” i “–” na evaluacijskim listovima.

Zadaci iz udžbenika:

• Posada – “sinus”: br. 118 g;
• Posada – “kosinus”: br. 122 a;
• Posada – “tangenta”: br. 123 g;
• Posada – “kotangens”: br. 125

Faza IV. Iznenadno zaustavljanje je nesreća.

– Auto ti se pokvario. Vaš auto treba popraviti.

Izjave su date za svaku posadu, ali u njima ima grešaka. Pronađite ove greške i objasnite zašto su nastale. Izjave koriste trigonometrijske funkcije koje odgovaraju marki vašeg automobila.

V faza. Stani.

Umorni ste i trebate se odmoriti. Dok se posada odmara, kormilari sumiraju preliminarne rezultate: broje "za" i "protiv" članova posade i posade u cjelini.

Za studente:

3 ili više “+” – rezultat “5”;
2 “+” – ocjena “4”;
1 “+” – ocjena “3”.

Za posade:“+” i “-” se međusobno poništavaju. Računaju se samo preostali znakovi.

Pogodi šaradu.

Od brojeva uzimaš moj prvi slog,
Drugi je od riječi “ponosan”.
I ti ćeš voziti treće konje,
Četvrti će biti blejanje ovce.
Moj peti slog je isti kao i prvi
Poslednje slovo u abecedi je šesto,
I ako sve tačno pogodiš,
Tada ćete iz matematike dobiti ovakav odjeljak.
(trigonometrija)

Riječ "trigonometrija" (od grčkih riječi "trigonon" - trokut i "metreo" - mjera) znači "mjera trouglova". Pojava trigonometrije povezana je s razvojem geografije i astronomije - nauke o kretanju nebeska tela, o strukturi i razvoju Univerzuma.

Kao rezultat izvršenih astronomskih opservacija, pojavila se potreba za određivanjem položaja svjetiljki, izračunavanjem udaljenosti i uglova. Budući da se neke udaljenosti, na primjer, od Zemlje do drugih planeta, nisu mogle direktno izmjeriti, naučnici su počeli razvijati tehnike za pronalaženje odnosa između stranica i uglova trougla, u kojem se dva vrha nalaze na zemlji, a treći je planeta ili zvijezda. Takvi odnosi se mogu izvesti proučavanjem različitih trouglova i njihovih svojstava. Zbog toga su astronomski proračuni doveli do rješenja (tj. pronalaženja elemenata) trougla. To radi trigonometrija.

Počeci trigonometrije otkriveni su u starom Babilonu. Babilonski naučnici su bili u stanju da predvide solarnu i pomračenja mjeseca. Neke informacije trigonometrijske prirode nalaze se u drevnim spomenicima drugih drevnih naroda.

Faza VI. Završi.

Da biste uspješno prešli ciljnu liniju, sve što trebate učiniti je napregnuti se i napraviti “sprint”. U trigonometriji je veoma važno moći brzo odrediti vrijednosti sin t, cost, tgt, ctg t, gdje je 0 ≤ t ≤ . Zatvorite udžbenike.

Ekipe se naizmjenično prozivaju vrijednosti. funkcije sin t, trošak, tgt, ctg t ako:

VII faza. Rezultati.

Rezultati utakmice.

Kormilari predaju evaluacijske listove. Određena je posada koja je postala šampion „Matematičkog mitinga“ i okarakterisan rad preostalih grupa. Slijede imena onih koji su dobili ocjene “5” i “4”.

Sažetak lekcije.

- Momci! Šta ste danas naučili na času? (pojednostavite trigonometrijske izraze; pronađite vrijednosti trigonometrijskih funkcija). Šta trebate znati za ovo?

• definicije i greh svojstava t, cos t, tg t, ctg t;
• relacije koje povezuju vrijednosti različitih trigonometrijskih funkcija;
• znakovi trigonometrijskih funkcija na četvrtinama brojevnog kruga.
• vrijednosti trigonometrijskih funkcija prve četvrtine brojevnog kruga.

– Mislim da razumete da morate dobro poznavati formule da biste ih pravilno primenili. Takođe ste shvatili da je trigonometrija veoma važan deo matematike, jer se koristi i u drugim naukama: astronomiji, geografiji, fizici itd.

Zadaća:

• za studente koji su dobili “5” i “4”: §6, br. 128a, 130a, 134a.
• za ostale učenike: §6, br. 119g, br. 120g, br. 121g.

Video lekcija “Trigonometrijske funkcije numeričkog argumenta” pruža vizuelni materijal za pružanje jasnoće prilikom objašnjavanja teme u razredu. Tokom demonstracije razmatra se princip formiranja vrijednosti trigonometrijskih funkcija iz broja, opisani su brojni primjeri koji uče kako izračunati vrijednosti trigonometrijskih funkcija iz broja. Uz pomoć ovog priručnika lakše je razviti vještine rješavanja relevantnih problema i postići pamćenje gradiva. Korištenje priručnika povećava učinkovitost lekcije i pomaže u brzom postizanju ciljeva učenja.

Na početku lekcije prikazuje se naslov teme. Tada je zadatak pronaći odgovarajući kosinus nekom numeričkom argumentu. Napominje se da ovaj zadatak Rješenje je jednostavno i može se jasno pokazati. Na ekranu se prikazuje jedinični krug sa središtem na početku. Primećuje se da se tačka preseka kružnice sa pozitivnom poluosom ose apscise nalazi u tački A(1;0). Dat je primjer tačke M koja predstavlja argument t=π/3. Ova tačka je označena na jedinični krug, a od nje se okomica spušta na osu apscise. Pronađena apscisa tačke je kosinus od cos t. U ovom slučaju, apscisa tačke će biti x=1/2. Stoga cos t=1/2.

Sumirajući razmotrene činjenice, napominje se da ima smisla govoriti o funkciji s=cos t. Napominje se da studenti već imaju određena znanja o ovoj funkciji. Izračunavaju se neke kosinusne vrijednosti: cos 0=1, cos π/2=0, cos π/3=1/2. Za ovu funkciju povezane su i funkcije s=sin t, s=tg t, s=ctg t. Napominje se da imaju zajednički naziv za sve - trigonometrijske funkcije.

Važni odnosi koji se koriste u rješavanju problema sa trigonometrijske funkcije: glavni identitet sin 2 t+ cos 2 t=1, izraz tangente i kotangensa kroz sinus i kosinus tg t=sin t/cos t, gdje je t≠π/2+πk za kϵZ, ctg t= cos t/sin t, gdje je t≠πk za kϵZ, kao i omjer tangente prema kotangensu tg t·ctg t=1 gdje je t≠πk/2 za kϵZ.

Zatim predlažemo da razmotrimo dokaz relacije 1+ tg 2 t=1/ cos 2 t, sa t≠π/2+πk za kϵZ. Da bismo dokazali identitet, potrebno je tg 2 t predstaviti u obliku omjera sinusa i kosinusa, a zatim dovesti članove na lijevoj strani na zajednički nazivnik 1+ tg 2 t=1+sin 2 t/cos 2 t = (sin 2 t+cos 2 t )/ cos 2 t. Koristeći osnovni trigonometrijski identitet, dobijamo 1 u brojiocu, odnosno konačni izraz 1/ cos 2 t. Q.E.D.

Identitet 1+ cot 2 t=1/ sin 2 t dokazuje se na sličan način, za t≠πk za kϵZ. Kao iu prethodnom dokazu, kotangens je zamijenjen odgovarajućim omjerom kosinusa i sinusa, a oba člana na lijevoj strani se svode na zajednički nazivnik 1+ cot 2 t=1+ cos 2 t/sin 2 t= ( sin 2 t+cos 2 t)/sin 2 t. Nakon nanošenja glavnog trigonometrijski identitet na brojilac dobijamo 1/ sin 2 t. Ovo je izraz koji tražimo.

Razmatra se rješenje primjera u kojima se stečeno znanje primjenjuje. U prvom zadatku morate pronaći vrijednosti cijene, tgt, ctgt, ako je poznat sinus broja sint=4/5, a t pripada intervalu π/2< t<π. Для нахождения косинуса в данном примере рекомендуется использовать тождество sin 2 t+ cos 2 t=1, из которого следует cos 2 t=1-sin 2 t. Зная значение синуса, можно найти косинус cos 2 t=1-(4/5) 2 =9/25. То есть значение косинуса cost=3/5 и cost=-3/5. В условии указано, что аргумент принадлежит второй четверти координатной плоскости. В этой четверти значение косинуса отрицательное. С учетом данного ограничения находим cost=-3/5. Для нахождения тангенса числа пользуемся его определением tgt= sint/cost. Подставив известные значения синуса и косинуса, получаем tgt=4/5:(-3/5)=-4/3. Чтобы найти значение котангенса, также используется определение котангенса ctgt= cost/sint. Подставив известные значения синуса и косинуса в отношение, получаем ctgt=(-3/5):4/5=-3/4.

Zatim razmatramo rješenje sličnog problema u kojem je poznata tangenta tgt = -8/15, a argument je ograničen na vrijednosti 3π/2

Da bismo pronašli vrijednost sinusa, koristimo definiciju tangente tgt= sint/cost. Iz njega nalazimo sint= tgt·cost=(-8/15)·(15/17)=-8/17. Znajući da je kotangens inverzna funkcija tangente, nalazimo ctgt=1/(-8/15)=-15/8.

Video lekcija „Trigonometrijske funkcije numeričkog argumenta“ koristi se za povećanje efikasnosti nastave matematike u školi. Tokom učenja na daljinu, ovaj materijal se može koristiti kao vizualna pomoć za razvijanje vještina u rješavanju problema koji uključuju trigonometrijske funkcije broja. Da bi stekao ove vještine, studentu se može savjetovati da samostalno pregleda vizuelni materijal.

DEKODIRANJE TEKSTA:

Tema lekcije je "Trigonometrijske funkcije numeričkog argumenta."

Bilo koji realan broj t može biti pridružen jednoznačno definiranom broju cos t. Da biste to uradili potrebno je da uradite sledeće:

1) postaviti brojevnu kružnicu na koordinatnu ravan tako da se centar kružnice poklapa sa ishodištem koordinata, a početna tačka A kružnice pada u tačku (1;0);

2) naći tačku na kružnici koja odgovara broju t;

3) naći apscisu ove tačke. Ovo je cos t.

Stoga ćemo govoriti o funkciji s = cos t (es je kosinus te), gdje je t bilo koji realan broj. Već imamo neku ideju o ovoj funkciji:

• naučili izračunati neke vrijednosti, na primjer cos 0=1, cos = 0, cos =, itd. (kosinus od nule je jednak jedan, kosinus od pi sa dva je jednak nuli, kosinus od pi od tri je jednako jednoj polovini i tako dalje).
• a pošto su vrijednosti sinusa, kosinusa, tangenta i kotangensa međusobno povezane, dobili smo ideju o još tri funkcije: s = sint; s= tgt; s= ctgt. (es jednako sinus te, es jednako tangenta te, es jednako kotangens te)

Sve ove funkcije nazivaju se trigonometrijskim funkcijama numeričkog argumenta t.

Iz definicija sinusa, kosinusa, tangenta i kotangensa slijede neki odnosi:

1) sin 2 t + cos 2 t = 1 (sinus kvadrat te plus kosinus kvadrat te jednako jedan)

2)tgt = za t ≠ + πk, kϵZ (tangenta te je jednaka omjeru sinusa te i kosinusa te pri čemu te nije jednako pi za dva plus pi ka, ka pripada zet)

3) ctgt = za t ≠ πk, kϵZ (kotangens te je jednak omjeru kosinusa te i sinusa te kada te nije jednako pi ka, ka pripada zet).

4) tgt ∙ ctgt = 1 za t ≠ , kϵZ (proizvod tangente te sa kotangensom te jednak je jedan kada te nije jednako vrhuncu ka, podijeljeno sa dva, ka pripada zet)

Dokažimo još dvije važne formule:

Jedan plus tangenta na kvadrat te je jednak omjeru jedan prema kosinus na kvadrat te kada te nije jednako pi sa dva plus pi ka.

Dokaz. Svedujmo izraz jedan plus tangenta na kvadrat te na zajednički nazivnik kosinus na kvadrat te. U brojiocu dobijamo zbir kvadrata kosinusa te i sinusa te, koji je jednak jedan. I imenilac ostaje kvadrat kosinusa te.

Zbir jedinice i kvadrata kotangensa te jednak je omjeru jedinice i kvadrata sinusa te kada te nije jednako pi ka.

Dokaz. Izraz jedan plus kotangens na kvadrat te, slično, dovodimo do zajedničkog nazivnika i primjenjujemo prvu relaciju.

Pogledajmo primjere.

PRIMJER 1. Pronađite cijenu, tgt, ctgt ako je sint = i< t < π.(если синус тэ равен четырем пятым и тэ из промежутка от пи на два до пи)

Rješenje. Iz prve relacije nalazimo da je kosinus na kvadrat te jednak jedan minus sinus na kvadrat te: cos 2 t = 1 - sin 2 t.

To znači da je cos 2 t = 1 -() 2 = (kosinus kvadrat te je jednak devet dvadeset petih), odnosno trošak = (kosinus te je jednak tri petine) ili trošak = - (kosinus te jednak minus tri petine). Po uslovu, argument t pripada drugoj četvrtini, au njoj cos t< 0 (косинус тэ отрицательный).

To znači da je kosinus te jednak minus tri petine, trošak = - .

Izračunajmo tangentu te:

tgt = = ׃ (-)= - ;(tangenta te je jednaka omjeru sinus te i kosinus te, dakle četiri petine prema minus tri petine i jednaka minus četiri trećine)

Shodno tome izračunavamo (kotangens broja te. pošto je kotangens te jednak omjeru kosinusa od te i sinusa od te,) ctgt = = - .

(kotangens te je jednak minus tri četvrtine).

Odgovor: trošak = - , tgt= - ; ctgt = - . (odgovor popunjavamo dok ga rješavamo)

PRIMJER 2. Poznato je da je tgt = - i< t < 2π(тангенс тэ равен минус восемь пятнадцатых и тэ принадлежит промежутку от трех пи на два до двух пи). Найти значения cost, sint, ctgt.

Rješenje. Koristimo ovaj odnos i zamijenimo vrijednost u ovu formulu da dobijemo:

1 + (-) 2 = (jedan po kosinus kvadratu te je jednak zbroju jedan i kvadrat minus osam petnaesti). Odavde nalazimo cos 2 t =

(kosinus kvadrat te je jednak dvjesta dvadeset i pet dvjesto osamdeset devetih). To znači trošak = (kosinus te je petnaest sedamnaestih) ili

trošak = . Po uslovu, argument t pripada četvrtom kvartalu, gdje je trošak>0. Prema tome trošak = .(kozenus te je petnaest sedamnaestih)

Nađimo vrijednost argumenta sine te. Pošto je iz relacije (prikaži relaciju tgt = za t ≠ + πk, kϵZ) sinus te jednak umnošku tangente te sa kosinusom te, onda je zamjena vrijednosti argumenta te..tangenta te jednaka minus osam petnaestih .. po uslovu, a kosinus te je jednak rešenom ranije, dobijamo

sint = tgt ∙ trošak = (-) ∙ = - , (sine te je jednako minus osam sedamnaestih)

ctgt = = - . (pošto je kotangens te recipročan tangent, što znači da je kotangens te jednak minus petnaest osamnaestih)