Rješavanje problema o ravnoteži konvergentnih sila konstruiranjem zatvorenih poligona sila uključuje glomazne konstrukcije. Univerzalna metoda za rješavanje ovakvih problema je prelazak na određivanje projekcija datih sila na koordinatne ose i rad sa tim projekcijama. Os je prava linija kojoj je dodijeljen određeni smjer.
Projekcija vektora na osu je skalarna veličina, koja je određena segmentom ose odsečenim okomicama koje su na nju spuštene sa početka i kraja vektora.
Vektorska projekcija se smatra pozitivnom ako se smjer od početka projekcije do njenog kraja poklapa s pozitivnim smjerom ose. Vektorska projekcija se smatra negativnom ako je smjer od početka projekcije do njenog kraja suprotan pozitivnom smjeru ose.
Dakle, projekcija sile na koordinatnu osu jednaka je proizvodu modula sile i kosinusa ugla između vektora sile i pozitivnog smera ose.
Razmotrimo nekoliko slučajeva projektovanja sila na osu:
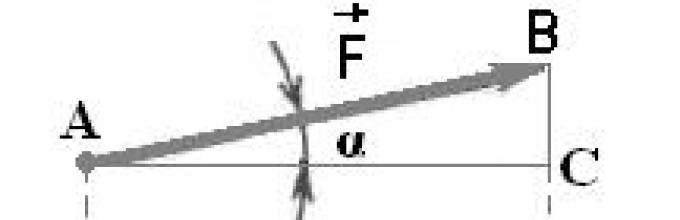
Vektor sile F(Sl. 15) pravi oštar ugao sa pozitivnim smerom x ose.

Da bismo pronašli projekciju, od početka i kraja vektora sile spuštamo okomice na osu oh; dobijamo
1. Fx = F cos α
Projekcija vektora u ovom slučaju je pozitivna
Force F(Sl. 16) je sa pozitivnim smjerom ose X tupi ugao α.

Onda F x = F cos α, ali pošto je α = 180 0 - φ,
F x = F cos α = F cos180 0 - φ =- F cos φ.
Projekcija sile F po osi oh u ovom slučaju je negativan.
Force F(Sl. 17) okomito na osu oh.

Projekcija sile F na osu X jednaka nuli
F x = F cos 90° = 0.
Sila se nalazi na avionu howe(Sl. 18), može se projicirati na dvije koordinatne ose Oh I OU.

Snaga F može se podijeliti na komponente: F x i F y. Vektorski modul F x je jednako projekciji vektora F po osi vol, i vektorski modul F y je jednako projekciji vektora F po osi oh.
Od Δ OAV: F x = F cos α, F x = F sin α.
Od Δ OAS: F x = F cos φ, F x = F sin φ.
Veličina sile se može naći pomoću Pitagorine teoreme:
![]()
Projekcija vektorskog zbira ili rezultante na bilo koju osu jednaka je algebarskom zbiru projekcija sabiraka vektora na istu osu.
Uzmite u obzir konvergentne sile F 1 , F 2 , F 3, i F 4, (Sl. 19, a). Geometrijski zbir ili rezultanta ovih sila F određena završnom stranom poligona sila


Spustimo se iz vrhova poligona sila na osu x okomite.
S obzirom na dobijene projekcije sila direktno iz završene konstrukcije, imamo
F= F 1x+ F 2x+ F 3x+ F 4x
gdje je n broj vektorskih pojmova. Njihove projekcije ulaze u gornju jednačinu sa odgovarajućim predznakom.
U ravni se geometrijski zbir sila može projicirati na dvije koordinatne ose, a u prostoru na tri.
Prvo, prisjetimo se šta je to koordinatna osa, projekcija tačke na osu I koordinate tačke na osi.
Koordinatna osa- Ovo je prava linija kojoj je dat neki pravac. Možete ga zamisliti kao vektor sa beskonačno velikim modulom.
Koordinatna osa označava se nekim slovom: X, Y, Z, s, t... Obično se (proizvoljno) na osi bira tačka koja se naziva ishodište i po pravilu se označava slovom O. Od ove tačke mjere se udaljenosti do drugih tačaka koje nas zanimaju.
Projekcija tačke na osu- ovo je osnova okomice spuštena iz ove tačke na ovu os (slika 8). To jest, projekcija tačke na osu je tačka.
Koordinata točke na osi- ovo je broj čija je apsolutna vrijednost jednaka dužini segmenta ose (na odabranoj skali) koji se nalazi između početka ose i projekcije tačke na ovu osu. Ovaj broj se uzima sa znakom plus ako se projekcija tačke nalazi u smjeru ose od njenog početka i sa znakom minus ako je u suprotnom smjeru.
Skalarna projekcija vektora na osu- Ovo broj, čija je apsolutna vrijednost jednaka dužini segmenta ose (na odabranoj skali) zatvorenog između projekcija početne i krajnje tačke vektora. Bitan! Obično umjesto izraza skalarna projekcija vektora na osu jednostavno kažu - projekcija vektora na osu, odnosno riječ skalar spušteno. Vektorska projekcija označava se istim slovom kao i projektovani vektor (normalnim, ne podebljanim slovima), sa nižim (u pravilu) indeksom naziva ose na koju se ovaj vektor projektuje. Na primjer, ako se vektor projektuje na os X A, tada je njegova projekcija označena sa x. Prilikom projektovanja istog vektora na drugu osu, recimo, Y osu, njegova projekcija će biti označena sa y (slika 9).

Da izračunam projekcija vektora na osu(npr. osa X), potrebno je oduzeti koordinatu početne tačke od koordinate njene krajnje tačke, tj.
a x = x k − x n.
Moramo zapamtiti: skalarna projekcija vektora na osu (ili, jednostavno, projekcija vektora na osu) je broj (ne vektor)!Štaviše, projekcija može biti pozitivna ako je vrijednost x k veća od vrijednosti x n, negativna ako je vrijednost x k manja od vrijednosti x n i jednaka nuli ako je x k jednako x n (slika 10).

Projekcija vektora na osu može se naći i poznavanjem modula vektora i ugla koji čini sa ovom osom.
Sa slike 11 je jasno da je a x = a Cos α
To jest, projekcija vektora na osu jednaka je proizvodu modula vektora i kosinusa ugla između smjera ose i smjera vektora. Ako je ugao oštar, onda je Cos α > 0 i a x > 0, a ako je tup, onda je kosinus tupog ugla negativan, a projekcija vektora na osu će također biti negativna.

Uglovi mjereni od ose u smjeru suprotnom od kazaljke na satu smatraju se pozitivnim, a uglovi mjereni duž ose su negativni. Međutim, pošto je kosinus parna funkcija, odnosno Cos α = Cos (− α), pri izračunavanju projekcija uglovi se mogu brojati i u smeru kazaljke na satu i u suprotnom smeru kazaljke na satu.
Prilikom rješavanja problema često će se koristiti sljedeća svojstva projekcija: ako
A = b + c +…+ d, tada a x = b x + c x +…+ d x (slično drugim osama),
a= m b, tada a x = mb x (slično za druge ose).
Formula a x = a Cos α će biti Često nastaju prilikom rješavanja problema, tako da to svakako trebate znati. Morate znati pravilo za određivanje projekcije srcem!
Zapamtite!
Da bi se pronašla projekcija vektora na osu, modul ovog vektora mora se pomnožiti sa kosinusom ugla između smjera ose i smjera vektora.
Još jednom - napamet!
Projekcija vektor na osu je vektor koji se dobija množenjem skalarne projekcije vektora na ovu osu i jediničnog vektora ove ose. Na primjer, ako je a x – skalarnu projekciju vektor A do ose X, zatim a x i- njegova vektorska projekcija na ovu osu.
Označimo vektorska projekcija isto kao i sam vektor, ali sa indeksom ose na koju se vektor projektuje. Dakle, vektorska projekcija vektora A na osi X koju označavamo A x ( debeo slovo koje označava vektor i indeks imena ose) ili (nepodebljano slovo koje označava vektor, ali sa strelicom na vrhu (!) i indeksom imena ose).
Skalarna projekcija vektor po osi se zove broj, čija je apsolutna vrijednost jednaka dužini segmenta ose (na odabranoj skali) zatvorenog između projekcija početne i krajnje tačke vektora. Obično umjesto izraza skalarnu projekciju jednostavno kažu - projekcija. Projekcija se označava istim slovom kao i projektovani vektor (normalnim, ne podebljanim slovima), sa nižim indeksom (u pravilu) naziva ose na koju se ovaj vektor projektuje. Na primjer, ako se vektor projektuje na os X A, tada je njegova projekcija označena sa x. Prilikom projektovanja istog vektora na drugu osu, ako je os Y, njena projekcija će biti označena sa y.
Za izračunavanje projekcije vektor na osi (npr. osi X) potrebno je oduzeti koordinatu početne tačke od koordinate njene krajnje tačke, tj.
a x = x k − x n.
Projekcija vektora na osu je broj.Štaviše, projekcija može biti pozitivna ako je vrijednost x k veća od vrijednosti x n,
negativan ako je vrijednost x k manja od vrijednosti x n
i jednako nuli ako je x k jednako x n.
Projekcija vektora na osu može se naći i poznavanjem modula vektora i ugla koji čini sa ovom osom.
Sa slike je jasno da je a x = a Cos α
odnosno, projekcija vektora na osu jednaka je umnošku modula vektora i kosinusa ugla između pravca ose i vektorski pravac. Ako je ugao oštar, onda
Cos α > 0 i a x > 0, a ako je tup, onda je kosinus tupog ugla negativan, a projekcija vektora na osu će također biti negativna.
Uglovi mjereni od ose u smjeru suprotnom od kazaljke na satu smatraju se pozitivnim, a uglovi mjereni duž ose su negativni. Međutim, pošto je kosinus parna funkcija, odnosno Cos α = Cos (− α), pri izračunavanju projekcija uglovi se mogu brojati i u smeru kazaljke na satu i u suprotnom smeru kazaljke na satu.
Da bi se pronašla projekcija vektora na osu, modul ovog vektora mora se pomnožiti sa kosinusom ugla između smjera ose i smjera vektora.
Vektorske koordinate— koeficijenti jedine moguće linearne kombinacije baznih vektora u odabranom koordinatnom sistemu, jednaki datom vektoru.
gdje su koordinate vektora.
Tačkasti proizvod vektora
Skalarni proizvod vektora[- u konačno-dimenzionalnom vektorski prostor definira se kao zbir proizvoda identičnih komponenti koje se množe vektori.
Na primjer, S.p.v. a = (a 1 , ..., a n) I b = (b 1 , ..., b n):
(a , b ) = a 1 b 1 + a 2 b 2 + ... + a n b n
Iz fizike za 9. razred (I.K.Kikoin, A.K.Kikoin, 1999.),
zadatak №5
u poglavlje" POGLAVLJE 1. OPĆE INFORMACIJE O SAOBRAĆAJU».
1. Šta se naziva projekcija vektora na koordinatnu osu?
1. Projekcija vektora a na osovinu koordinata je dužina odsječka između projekcija početka i kraja vektora a (okomice spuštene iz ovih tačaka na osu) na ovu koordinatnu osu.
2. Kako je vektor pomaka tijela povezan s njegovim koordinatama?
2. Projekcije vektora pomaka s na koordinatne ose jednake su promjeni odgovarajućih koordinata tijela.
3. Ako se koordinata tačke vremenom povećava, koji predznak ima projekcija vektora pomaka na osu koordinata? Šta ako se smanji?
3. Ako se koordinata tačke povećava tokom vremena, tada će projekcija vektora pomaka na koordinatnu osu biti pozitivna, jer u ovom slučaju ćemo ići od projekcije početka do projekcije kraja vektora u pravcu same ose.
Ako se koordinata tačke smanjuje tokom vremena, tada će projekcija vektora pomaka na koordinatnu osu biti negativna, jer u ovom slučaju ćemo ići od projekcije početka do projekcije kraja vektora na vodilicu same ose.
4. Ako je vektor pomaka paralelan sa X osom, koliki je onda modul projekcije vektora na ovu osu? A šta je sa modulom projekcije istog vektora na Y osu?
4. Ako je vektor pomaka paralelan sa X osom, tada je modul projekcije vektora na ovu osu jednak modulu samog vektora, a njegova projekcija na Y osu je nula.
5. Odrediti predznake projekcija na X osu vektora pomaka prikazanih na slici 22. Kako se mijenjaju koordinate tijela pri tim pomacima?
5. U svim sljedećim slučajevima, Y koordinata tijela se ne mijenja, a X koordinata tijela će se promijeniti na sljedeći način:
a) s 1;
projekcija vektora s 1 na osu X je negativna i jednaka je po apsolutnoj vrijednosti dužini vektora s 1 . S takvim kretanjem, X koordinata tijela će se smanjiti za dužinu vektora s 1.
b) s 2 ;
projekcija vektora s 2 na osu X je pozitivna i jednaka je po veličini dužini vektora s 1 . Sa takvim kretanjem, X koordinata tijela će se povećati za dužinu vektora s 2.
c) s 3 ;
projekcija vektora s 3 na osu X je negativna i jednaka je po veličini dužini vektora s 3 . Kod takvog kretanja, X koordinata tijela će se smanjiti za dužinu vektora s 3.
d)s 4;
projekcija vektora s 4 na osu X je pozitivna i jednaka je po veličini dužini vektora s 4 . Sa takvim kretanjem, X koordinata tijela će se povećati za dužinu vektora s 4.
e) s 5;
projekcija vektora s 5 na osu X je negativna i jednaka je po veličini dužini vektora s 5 . Kod takvog kretanja, X koordinata tijela će se smanjiti za dužinu vektora s 5.
6. Ako je vrijednost prijeđenog puta velika, može li modul pomaka biti mali?
6. Možda. To je zbog činjenice da je pomak (vektor pomaka) vektorska veličina, tj. je usmjereni pravi segment koji povezuje početni položaj tijela s njegovim kasnijim položajima. A konačni položaj tijela (bez obzira na pređenu udaljenost) može biti koliko god želite bliži početnom položaju tijela. Ako se konačni i početni položaj tijela poklapaju, modul pomaka će biti jednak nuli.
7. Zašto je vektor kretanja tijela važniji u mehanici od putanje koje je prešlo?
7. Glavni zadatak mehanike je da u svakom trenutku odredi položaj tijela. Poznavajući vektor kretanja tijela možemo odrediti koordinate tijela, tj. položaj tijela u bilo kojem trenutku, a znajući samo prijeđeni put, ne možemo odrediti koordinate tijela, jer nemamo informaciju o smjeru kretanja, već možemo samo prosuditi dužinu pređenog puta u datom trenutku.
Osa je pravac. To znači da se projekcija na osu ili na usmjerenu liniju smatra istom. Projekcija može biti algebarska ili geometrijska. U geometrijskom smislu, projekcija vektora na osu se shvata kao vektor, a u algebarskom smislu kao broj. Odnosno, koriste se koncepti projekcije vektora na osu i numeričke projekcije vektora na osu.
Ako imamo L os i vektor različit od nule A B →, onda možemo konstruisati vektor A 1 B 1 ⇀, označavajući projekcije njegovih tačaka A 1 i B 1.
A 1 B → 1 će biti projekcija vektora A B → na L.
Definicija 1
Projekcija vektora na osu je vektor čiji su početak i kraj projekcije početka i kraja datog vektora. n p L A B → → uobičajeno je označavati projekciju A B → na L. Da bi se konstruisala projekcija na L, okomite se spuštaju na L.
Primjer 1
Primjer vektorske projekcije na osu.
Na koordinatnoj ravni O x y navedena je tačka M 1 (x 1, y 1). Potrebno je konstruisati projekcije na O x i O y da bi se prikazao radijus vektor tačke M 1. Dobijamo koordinate vektora (x 1, 0) i (0, y 1).

Ako govorimo o projekciji a → na b → različit od nule ili projekciji a → na pravac b → , onda mislimo na projekciju a → na osu s kojom se poklapa pravac b →. Projekcija a → na pravu definisanu sa b → označava se n p b → a → → . Poznato je da kada se ugao između a → i b → , n p b → a → → i b → može smatrati kosmjernim. U slučaju kada je ugao tup, n p b → a → → i b → su u suprotnim smjerovima. U situaciji okomitosti a → i b →, i a → je nula, projekcija a → u pravcu b → je nulti vektor.
Numerička karakteristika projekcije vektora na osu je numerička projekcija vektora na datu osu.
Definicija 2
Numerička projekcija vektora na osu je broj koji je jednak proizvodu dužine datog vektora i kosinusa ugla između datog vektora i vektora koji određuje smjer ose.
Numerička projekcija A B → na L označava se n p L A B → , a a → na b → - n p b → a → .
Na osnovu formule dobijamo n p b → a → = a → · cos a → , b → ^ , odakle je a → dužina vektora a → , a ⇀ , b → ^ ugao između vektora a → i b → .
Dobijamo formulu za izračunavanje numeričke projekcije: n p b → a → = a → · cos a → , b → ^ . Primjenjivo je za poznate dužine a → i b → i ugao između njih. Formula je primjenjiva za poznate koordinate a → i b →, ali postoji pojednostavljeni oblik.
Primjer 2
Odrediti numeričku projekciju a → na pravu u pravcu b → sa dužinom a → jednakom 8 i uglom između njih od 60 stepeni. Po uslovu imamo a ⇀ = 8, a ⇀, b → ^ = 60°. To znači da numeričke vrijednosti zamjenjujemo u formulu n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .
odgovor: 4.
Sa poznatim cos (a → , b → ^) = a ⇀ , b → a → · b → , imamo a → , b → kao skalarni proizvod a → i b → . Slijedeći formulu n p b → a → = a → · cos a ⇀, b → ^, možemo pronaći numeričku projekciju a → usmjerenu duž vektora b → i dobiti n p b → a → = a → , b → b → . Formula je ekvivalentna definiciji datoj na početku pasusa.
Definicija 3
Numerička projekcija vektora a → na osu koja se poklapa u pravcu sa b → je odnos skalarnog proizvoda vektora a → i b → na dužinu b → . Formula n p b → a → = a → , b → b → je primenljiva za pronalaženje numeričke projekcije a → na pravu koja se poklapa u pravcu sa b → , sa poznatim a → i b → koordinatama.
Primjer 3
Dato je b → = (- 3 , 4) . Pronađite numeričku projekciju a → = (1, 7) na L.
Rješenje
Na koordinatnoj ravni n p b → a → = a → , b → b → ima oblik n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , sa a → = (a x , a y ) i b → = b x , b y . Da biste pronašli numeričku projekciju vektora a → na osu L, potrebno je: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.
odgovor: 5.
Primjer 4
Naći projekciju a → na L, koja se poklapa sa pravcem b →, gdje postoje a → = - 2, 3, 1 i b → = (3, - 2, 6). Naveden je trodimenzionalni prostor.
Rješenje
Za a → = a x , a y , a z i b → = b x , b y , b z , izračunavamo skalarni proizvod: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Dužina b → se nalazi pomoću formule b → = b x 2 + b y 2 + b z 2 . Iz toga slijedi da će formula za određivanje numeričke projekcije a → biti: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .
Zamijenite numeričke vrijednosti: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .
Odgovor: - 6 7.
Pogledajmo vezu između a → na L i dužine projekcije a → na L. Nacrtajmo osu L, dodajući a → i b → iz tačke na L, nakon čega povučemo okomitu liniju od kraja a → do L i nacrtamo projekciju na L. Postoji 5 varijacija slike:

Prvo slučaj sa a → = n p b → a → → znači a → = n p b → a → → , dakle n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .
Sekunda slučaj implicira upotrebu n p b → a → ⇀ = a → · cos a → , b → , što znači n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .
Treće slučaj objašnjava da kada je n p b → a → → = 0 → dobijamo n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , tada je n p b → a → → = 0 i n p b → a → = 0 = n p b → a → → .
Četvrto slučaj pokazuje n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , slijedi n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .
Peto slučaj pokazuje a → = n p b → a → → , što znači a → = n p b → a → → , dakle imamo n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .
Definicija 4
Numerička projekcija vektora a → na osu L, koja je usmjerena na isti način kao b →, ima sljedeću vrijednost:
- dužina projekcije vektora a → na L, pod uslovom da je ugao između a → i b → manji od 90 stepeni ili jednak 0: n p b → a → = n p b → a → → uz uslov 0 ≤ (a → , b →) ^< 90 ° ;
- nula pod uslovom da su a → i b → okomiti: n p b → a → = 0, kada je (a → , b → ^) = 90 °;
- dužina projekcije a → na L, pomnožena sa -1, kada postoji tup ili pravi ugao vektora a → i b →: n p b → a → = - n p b → a → → sa uslovom od 90 °< a → , b → ^ ≤ 180 ° .
Primjer 5
S obzirom na dužinu projekcije a → na L, jednaku 2. Pronađite numeričku projekciju a → pod uslovom da je ugao 5 π 6 radijana.
Rješenje
Iz uslova je jasno da je ovaj ugao tup: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .
Odgovor: - 2.
Primjer 6
Zadata je ravan O x y z vektorske dužine a → jednaka 6 3, b → (- 2, 1, 2) sa uglom od 30 stepeni. Pronađite koordinate projekcije a → na osu L.
Rješenje
Prvo izračunamo numeričku projekciju vektora a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
Po uslovu, ugao je oštar, tada je numerička projekcija a → = dužina projekcije vektora a →: n p L a → = n p L a → → = 9. Ovaj slučaj pokazuje da su vektori n p L a → → i b → kousmjereni, što znači da postoji broj t za koji je tačna jednakost: n p L a → → = t · b → . Odavde vidimo da je n p L a → → = t · b → , što znači da možemo pronaći vrijednost parametra t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .
Tada je n p L a → → = 3 · b → sa koordinatama projekcije vektora a → na osu L jednakom b → = (- 2 , 1 , 2) , gdje je potrebno vrijednosti pomnožiti sa 3. Imamo n p L a → → = (- 6 , 3 , 6) . Odgovor: (- 6, 3, 6).
Potrebno je ponoviti prethodno naučene informacije o stanju kolinearnosti vektora.
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter