Projekat iz algebre "Rješavanje trigonometrijskih nejednačina" Izvršila učenica 10. "B" razreda Kazačkova Julija Rukovodilac: nastavnik matematike Kochakova N.N.
Svrha Objediniti gradivo na temu "Rješavanje trigonometrijskih nejednačina" i izraditi dopis za učenike za pripremu za predstojeći ispit.
Ciljevi Sažeti materijal na ovu temu. Organizujte primljene informacije. Razmislite ovu temu na ispitu.
Relevantnost Relevantnost teme koju sam odabrao je da su zadaci na temu "Rješavanje trigonometrijskih nejednačina" uključeni u ispitne zadatke.
Trigonometrijske nejednakosti Nejednakost je odnos koji povezuje dva broja ili izraza pomoću jednog od znakova: (veće od); ≥ (veće ili jednako). Trigonometrijska nejednakost je nejednakost koja sadrži trigonometrijske funkcije.
Trigonometrijske nejednačine Rješenje nejednačina koje sadrže trigonometrijske funkcije svodi se po pravilu na rješenje najjednostavnijih nejednačina oblika: sin x> a, sin x a, cos x a, tg x a, ctg x
Algoritam za rješavanje trigonometrijskih nejednačina Na osi koja odgovara datoj trigonometrijskoj funkciji označiti datu brojčanu vrijednost te funkcije. Nacrtajte pravu liniju kroz označenu tačku koja seče jedinični krug. Odaberite točke presjeka prave i kružnice, uzimajući u obzir strogi ili nestrogi znak nejednakosti. Odaberite luk kruga na kojem se nalaze rješenja nejednačine. Odredite vrijednosti uglova na početnoj i krajnjoj tački kružnog luka. Zapišite rješenje nejednačine uzimajući u obzir periodičnost date trigonometrijske funkcije.
Formule za rješavanje trigonometrijskih nejednačina sinx> a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosxa; x (arktan a + πn; + πn). tgx a; x (πn; arktan + πn). ctgx
Grafičko rješenje osnovne trigonometrijske nejednakosti sinx> a
Grafičko rješenje osnovnih trigonometrijskih nejednačina sinx Grafičko rješenje osnovnih trigonometrijskih nejednačina cosx> a Grafičko rješenje glavnih trigonometrijskih nejednačina cosx Grafičko rješenje glavnih trigonometrijskih nejednačina tgx> a Grafičko rješenje osnovnih trigonometrijskih nejednačina tgx Grafičko rješenje glavnih trigonometrijskih nejednačina ctgx> a
Nejednakosti su relacije oblika a ›b, gdje su a i b izrazi koji sadrže barem jednu varijablu. Nejednakosti mogu biti stroge - ‹,› i nestroge - ≥, ≤.
Trigonometrijske nejednakosti su izrazi oblika: F (x) ›a, F (x)‹ a, F (x) ≤ a, F (x) ≥ a, u kojima je F (x) predstavljen jednom ili više trigonometrijskih funkcija .
Primjer najjednostavnije trigonometrijske nejednakosti je: sin x ‹1/2. Prihvaćeno je da se takvi problemi rješavaju grafički, za to su razvijene dvije metode.
Metoda 1 - Riješite nejednačine crtanjem funkcije
Da biste pronašli interval koji zadovoljava uslove nejednakosti sin x ‹1/2, morate izvršiti sljedeće korake:
- Izgradite sinusoidu y = sin x na koordinatnoj osi.
- Nacrtajte grafik na istoj osi numerički argument nejednakost, odnosno prava koja prolazi kroz tačku ½ ordinate OY.
- Označite tačke preseka dva grafikona.
- Zasenčite segment koji je rješenje za primjer.
Kada su u izrazu prisutni jaki znaci, tačke preseka nisu rešenja. Budući da je najmanji pozitivni period sinusoida 2π, odgovor pišemo na sljedeći način:
![]()
Ako predznaci izraza nisu strogi, tada se interval rješenja mora staviti u uglaste zagrade -. Odgovor na problem se također može napisati u obliku sljedeće nejednakosti: ![]()
Metoda 2 - Rješavanje trigonometrijskih nejednačina korištenjem jediničnog kruga
Slični zadaci se lako mogu riješiti uz pomoć trigonometrijski krug... Algoritam za pronalaženje odgovora je vrlo jednostavan:
- Prvo nacrtajte jedinični krug.
- Zatim je potrebno zabilježiti vrijednost lučne funkcije argumenta desne strane nejednakosti na luku kružnice.
- Potrebno je povući pravu liniju koja prolazi kroz vrijednost funkcije luka paralelno sa apscisnom osom (OX).
- Nakon toga, ostaje samo odabrati luk kruga, koji je skup rješenja trigonometrijske nejednakosti.
- Zapišite odgovor u traženom obliku.
Analizirajmo korake rješenja na primjeru nejednakosti sin x ›1/2. Na kružnici su označene tačke α i β - vrijednosti
![]()
Tačke luka koje se nalaze iznad α i β su interval za rješavanje date nejednačine.

Ako trebate riješiti primjer za cos, tada će luk odgovora biti lociran simetrično na os OX, a ne na OY. Da biste razmotrili razliku između intervala rješenja za sin i cos, možete koristiti dijagrame ispod u tekstu.

Grafička rješenja za tangentne i kotangensne nejednakosti će se razlikovati i od sinusa i od kosinusa. To je zbog svojstava funkcija.

Tangenta luka i kotangens luka su tangente na trigonometrijski krug, a minimalni pozitivni period za obje funkcije je π. Da biste brzo i ispravno koristili drugu metodu, morate zapamtiti na kojoj su osi iscrtane vrijednosti sin, cos, tg i ctg.
Tangentna tangenta ide paralelno sa OY osom. Ako stavite vrijednost arktana a na jedinični krug, tada će se druga tražena točka nalaziti u dijagonalnoj četvrtini. Uglovi
To su prijelomne tačke za funkciju, prema čemu graf teži, ali nikada ne dostigne.

U slučaju kotangensa, tangenta ide paralelno sa OX osom, a funkcija je prekinuta u tačkama π i 2π.

Kompleksne trigonometrijske nejednakosti
Ako je argument funkcije nejednakosti predstavljen ne samo promjenljivom, već i cjelobrojnim izrazom koji sadrži nepoznanicu, tada već govorimo o kompleksne nejednakosti... Tijek i redoslijed njegovog rješavanja donekle se razlikuju od gore opisanih metoda. Pretpostavimo da je potrebno pronaći rješenje sljedeće nejednakosti:

Grafičko rješenje predviđa konstrukciju obične sinusoide y = sin x po proizvoljno odabranim vrijednostima x. Hajde da izračunamo tabelu sa koordinatama za tačke stožera grafa:

Rezultat bi trebao biti lijepa kriva.
Radi jednostavnosti pronalaženja rješenja, zamijenite argument kompleksne funkcije

Presjek dva grafikona omogućava vam da odredite područje željenih vrijednosti na kojem je zadovoljen uvjet nejednakosti.

Pronađeni segment je rješenje za varijablu t:

Međutim, cilj potrage je pronaći sve moguće opcije nepoznato x:

Rješavanje dvostruke nejednakosti je prilično jednostavno, potrebno je premjestiti π / 3 na krajnje dijelove jednadžbe i izvršiti potrebne proračune:

Odgovorite na zadatak bi izgledalo kao interval za strogu nejednakost:

Takvi zadaci će zahtijevati od učenika iskustvo i spretnost u rukovanju trigonometrijskim funkcijama. Više zadaci obukeće se odlučiti u procesu pripreme, na koji će učenik lakše i brže pronaći odgovor ispitno pitanje test.
DEFINICIJA
Trigonometrijske nejednakosti su nejednakosti koje sadrže varijablu pod znakom trigonometrijske funkcije.
Rješavanje trigonometrijskih nejednačina
Rješavanje trigonometrijskih nejednačina se često svodi na rješavanje najjednostavnijih trigonometrijskih nejednačina oblika: \ (\ \ sin xa \), \ (\ \ cos x> a \), \ (\ \ ime operatora (tg) x> a \), \ (\ \ ime operatora (ctg) x> a \), \ (\ \ sin x \ leq a \), \ (\ \ cos x \ leq a \), \ (\ \ ime operatora (tg) x \ leq a \ ), \ (\ \ ime operatora (ctg) x \ leq a \), \ (\ \ sin x \ geq a \), \ (\ \ cos \ geq a \), \ (\ \ ime operatora (tg) x \ geq a \ ), \ (\ \ ime operatora (tg) x \ geq a \)
Najjednostavnije trigonometrijske nejednakosti rješavaju se grafički ili pomoću jediničnog trigonometrijskog kruga.
Po definiciji, sinus ugla \ (\ \ alpha \) je ordinata tačke \ (\ P _ (\ alpha) (x, y) \) jedinične kružnice (slika 1), a kosinus je apscisa ove tačke. Ova činjenica se koristi za rješavanje najjednostavnijih trigonometrijskih nejednakosti s kosinusom i sinusom koristeći jedinični krug.
Primjeri rješavanja trigonometrijskih nejednačina
Riješite nejednačinu \ (\ \ sin x \ leq \ frac (\ sqrt (3)) (2) \)
Budući da \ (\ \ lijevo | \ frac (\ sqrt (3)) (2) \ desno |, ova nejednačina ima rješenje i može se riješiti na dva načina
Prvi način. Rešimo ovu nejednačinu grafički. Da biste to učinili, konstruirajte u jednom koordinatnom sistemu graf sinusa \ (\ y = \ sin x \) (slika 2) i prave linije \ (\ y = \ frac (\ sqrt (3)) (2) \)
Odaberite intervale u kojima se sinusoida nalazi ispod grafika prave linije \ (\ y = \ frac (\ sqrt (3)) (2) \). Pronađite apscise \ (\ x_ (1) \) i \ (\ x_ (2) \) presečnih tačaka ovih grafova: \ (\ x_ (1) = \ pi- \ arcsin \ frac (\ sqrt (3) )) (2 ) = \ pi- \ frac (\ pi) (3) = \ frac (2 \ pi) (3) x_ (2) = \ arcsin \ frac (\ sqrt (3)) (2) +2 \ pi = \ frac (\ pi) (3) +2 \ pi = \ frac (7 \ pi) (3) \)
Dobili smo interval \ (\ \ lijevo [- \ frac (4 \ pi) (3); \ frac (\ pi) (3) \ desno] \) ali pošto je funkcija \ (\ y = \ sin x \) je periodičan i ima period \ (\ 2 \ pi \), onda je odgovor unija intervala: \ (\ \ lijevo [\ frac (2 \ pi) (3) +2 \ pi k; \ frac ( 7 \ pi) (3) + 2 \ pi k \ desno] \), \ (\ k \ u Z \)
Drugi način. Konstruirajte jediničnu kružnicu i pravu \ (\ y = \ frac (\ sqrt (3)) (2) \), označite njihove točke sjecišta \ (\ P_ (x_ (1)) \) i \ (\ P_ (x_ ( 2 )) \) (sl. 3). Rješenje izvorne nejednakosti je skup ordinatnih tačaka koje su manje od \ (\ \ frac (\ sqrt (3)) (2) \). Pronađite vrijednost \ (\ \ boldsymbol (I) _ (1) \) i \ (\ \ boldsymbol (I) _ (2) \), idući u smjeru suprotnom od kazaljke na satu, \ (\ x_ (1) Fig. 3
\ (\ x_ (1) = \ pi- \ arcsin \ frac (\ sqrt (3)) (2) = \ pi- \ frac (\ pi) (3) = \ frac (2 \ pi) (3) x_ (2) = \ arcsin \ frac (\ sqrt (3)) (2) +2 \ pi = \ frac (\ pi) (3) +2 \ pi = \ frac (7 \ pi) (3) \)
Uzimajući u obzir periodičnost sinusne funkcije, konačno dobijamo intervale \ (\ \ lijevo [\ frac (2 \ pi) (3) +2 \ pi k; \ frac (7 \ pi) (3) +2 \ pi \ desno] \), \ (\ k \ u Z \)
Riješite nejednačinu \ (\ \ sin x> 2 \)
Sinus je ograničena funkcija: \ (\ | \ sin x | \ leq 1 \), a desna strana ove nejednakosti je veća od jedan, tako da nema rješenja.
Riješite nejednačinu \ (\ \ cos x> \ frac (1) (2) \)
Ova nejednakost se može riješiti na dva načina: grafički i pomoću jediničnog kruga. Razmotrimo svaki od načina.
Prvi način. Predstavimo u istom koordinatnom sistemu funkcije koje opisuju lijevu i desnu stranu nejednakosti, odnosno \ (\ y = \ cos x \) i \ (\ y = \ frac (1) (2) \). Odaberimo intervale na kojima se graf kosinusne funkcije \ (\ y = \ cos x \) nalazi iznad grafika prave linije \ (\ y = \ frac (1) (2) \) (Sl. 4 ).
Pronađite apscisu tačaka \ (\ \ podebljani simbol (x) _ (1) \) i \ (\ x_ (2) \) - točke presjeka grafova funkcija \ (\ y = \ cos x \) i \ (\ y = \ frac (1) (2) \), koji su krajevi jednog od intervala na kojima vrijedi navedena nejednakost. \ (\ x_ (1) = - \ arccos \ frac (1) (2) = - \ frac (\ pi) (3) \); \ (\ x_ (1) = \ arccos \ frac (1) (2) = \ frac (\ pi) (3) \)
S obzirom da je kosinus periodična funkcija, sa periodom \ (\ 2 \ pi \), odgovor će biti vrijednosti \ (\ x \) iz intervala \ (\ \ lijevo (- \ frac (\ pi ) (3) +2 \ pi k; \ frac (\ pi) (3) +2 \ pi k \ desno) \), \ (\ k \ u Z \)
Drugi način. Konstruirajte jediničnu kružnicu i pravu \ (\ x = \ frac (1) (2) \) (od jedinični krug x-osa odgovara kosinusima). Označavamo \ (\ P_ (x_ (1)) \) i \ (\ P_ (x_ (2)) \) (slika 5) - tačke preseka prave i jedinične kružnice. Rješenje originalne jednadžbe će biti skup tačaka apscise koje su manje od \ (\ \ frac (1) (2) \). Pronađite vrijednost \ (\ x_ (1) \) i \ (\ 2 \), idući u smjeru suprotnom od kazaljke na satu tako da \ (\ x_ (1) Uzimajući u obzir periodičnost kosinusa, konačno dobijamo intervale \ (\ \ lijevo (- \ frac (\ pi) (3) +2 \ pi k; \ frac (\ pi) (3) +2 \ pi k \ desno) \), \ (\ k \ in Z \)
Riješite nejednačinu \ (\ \ ime operatora (ctg) x \ leq- \ frac (\ sqrt (3)) (3) \)
Konstruirajmo u jednom koordinatnom sistemu grafove funkcija \ (\ y = \ operatorname (ctg) x \), \ (\ y = - \ frac (\ sqrt (3)) (3) \)
Odaberite intervale u kojima se graf funkcije \ (\ y = \ operatorname (ctg) x \) ne nalazi iznad grafika prave linije \ (\ y = - \ frac (\ sqrt (3)) (3) \) (Sl. 6) ...
Pronađite apscisu tačke \ (\ x_ (0) \), koja je kraj jednog od intervala u kojem je nejednakost \ (\ x_ (0) = \ ime operatora (arcctg) \ lijevo (- \ frac (\ sqrt (3)) ( 3) \ desno) = \ pi- \ ime operatora (arcctg) \ lijevo (\ frac (\ sqrt (3)) (3) \ desno) = \ pi- \ frac (\ pi) (3) = \ frac (2 \ pi) (3) \)
Drugi kraj ovog intervala je tačka \ (\ \ pi \), a funkcija \ (\ y = \ ime operatora (ctg) x \) je nedefinisana u ovoj tački. Dakle, jedno od rješenja ove nejednakosti je interval \ (\ \ frac (2 \ pi) (3) \ leq x
Trigonometrijske nejednakosti sa složenim argumentom
Trigonometrijske nejednakosti sa složenim argumentom mogu se svesti na najjednostavnije trigonometrijske nejednakosti upotrebom zamjene. Nakon rješavanja, vrši se obrnuta zamjena i izražava se originalna nepoznata.
Riješite nejednačinu \ (\ 2 \ cos \ lijevo (2 x + 100 ^ (\ circ) \ desno) \ leq-1 \)
Izrazimo kosinus na desnoj strani ove nejednakosti: \ (\ \ cos \ lijevo (2 x + 100 ^ (\ circ) \ desno) \ leq- \ frac (1) (2) \)
Zamijenimo \ (\ t = 2 x + 100 ^ (\ circ) \), nakon čega se ova nejednakost transformira u najjednostavniju nejednakost \ (\ \ cos t \ leq- \ frac (1) (2) \)
Rešimo ga pomoću jediničnog kruga. Konstruirajte jediničnu kružnicu i pravu \ (\ x = - \ frac (1) (2) \). Neka su \ (\ P_ (1) \) i \ (\ P_ (2) \) tačke preseka prave i jedinične kružnice (slika 7).
Rješenje izvorne nejednakosti bit će skup tačaka apscisa, koje nisu veće od \ (\ - \ frac (1) (2) \). Tačka \ (\ P_ (1) \) odgovara uglu \ (\ 120 ^ (\ circ) \), a tačka \ (\ P_ (2) \). Dakle, s obzirom na period kosinusa, dobijamo \ (\ 120 ^ (\ circ) +360 ^ (\ circ) \ cdot n \ leq t \ leq 240 ^ (\ circ) +360 ^ (\ circ) \ cdot n \ ) , \ (\ n \ u Z \)
Napravimo obrnutu promjenu \ (\ t = 2 x + 100 ^ (\ circ) 120 ^ (\ circ) +360 ^ (\ circ) \ cdot n \ leq 2 x + 100 ^ (\ circ) \ leq 240 ^ (\ circ) +360 ^ (\ circ) \ cdot n \), \ (\ n \ u Z \)
Izražavamo \ (\ \ mathbf (x) \), za ovo prvo oduzimamo od svakog dijela nejednakosti \ (\ 100 ^ (\ circ) 120 ^ (\ circ) -100 ^ (\ circ) +360 ^ (\ circ) \ cdot n \ leq 2 x + 100 ^ (\ circ) -100 ^ (\ circ) \ leq 240 ^ (\ circ) -100 ^ (\ circ) +360 ^ (\ circ) \ cdot n \) , \ ( \ n \ u Z \); \ (\ 20 ^ (\ circ) +360 ^ (\ circ) \ cdot n \ leq 2 x \ leq 140 ^ (\ circ) +360 ^ (\ circ) \ cdot n \), \ (\ n \ in Z \)
a zatim podijelite sa 2 \ (\ \ frac (20 ^ (\ circ) +360 ^ (\ circ) \ cdot n) (2) \ leq \ frac (2 x) (2) \ leq \ frac (140 ^ ( \ circ) +360 ^ (\ circ) \ cdot n) (2) \), \ (\ n \ u Z \); \ (\ 10 ^ (\ circ) +180 ^ (\ circ) \ cdot n \ leq x \ leq 70 ^ (\ circ) +180 ^ (\ circ) \ cdot n \), \ (\ n \ u Z \)
Dvostruke trigonometrijske nejednakosti
Riješite dvostruku trigonometrijsku nejednačinu \ (\ \ frac (1) (2)
Uvodimo zamjenu \ (\ t = \ frac (x) (2) \), tada originalna nejednakost poprima oblik \ (\ \ frac (1) (2)
Rešimo ga pomoću jediničnog kruga. Budući da os ordinata odgovara sinusu na jediničnom krugu, odaberite na njoj skup ordinata koje su veće od \ (\ x = \ frac (1) (2) \) i manje od ili jednake \ (\ \ frac (\ sqrt (2)) (2 ) \). Na slici 8 ove tačke će se nalaziti na lukovima \ (\ P_ (t_ (1)) \), \ (\ P_ (t_ (2)) \) i \ (\ P_ (t_ (3)) \), \ ( \ P_ (t_ (4)) \). Pronađite vrijednost \ (\ t_ (1) \), \ (\ t_ (2) \), \ (\ t_ (3) \), \ (\ t_ (4) \), idući u smjeru suprotnom od kazaljke na satu, i \ (\ t_ (1) \ (\ t_ (3) = \ pi- \ arcsin \ frac (\ sqrt (2)) (2) = \ pi- \ frac (\ pi) (4) = \ frac (3 \ pi) (4) \);\ (\ t_ (4) = \ pi- \ arcsin \ frac (1) (2) = \ pi- \ frac (\ pi) (6) = \ frac (5 \ pi) (6 ) \)
Tako dobijamo dva intervala, koji se, uzimajući u obzir periodičnost sinusne funkcije, mogu zapisati na sledeći način \ (\ \ frac (\ pi) (6) +2 \ pi k \ leq t \ frac (\ pi) (4) +2 \ pi k \ quad \ frac (3 \ pi) (4) +2 \ pi k Napravite obrnutu promjenu \ (\ t = \ frac (x) (2) \ frac (\ pi) (6 ) +2 \ pi k \ leq \ frac (x) (2) \ frac (\ pi) (4) +2 \ pi k \), \ (\ \ frac (3 \ pi) (4) +2 \ pi k Express \ (\ \ mathbf ( x) \), za ovo pomnožimo sve strane pozadine nejednačina sa 2, dobićemo \ (\ \ frac (\ pi) (3) +4 \ pi k \ leq x
U praktičnoj lekciji ćemo razmotriti glavne vrste zadataka iz teme "Trigonometrija", dodatno analizirati zadatke povećane složenosti i razmotriti primjere rješavanja različitih trigonometrijskih nejednačina i njihovih sistema.
Ova lekcija će vam pomoći da se pripremite za jednu od vrsta zadataka B5, B7, C1 i C3.
Počnimo s ponavljanjem glavnih vrsta zadataka o kojima smo razgovarali u temi "Trigonometrija" i riješit ćemo nekoliko nestandardnih zadataka.
Problem broj 1... Pretvorite uglove u radijane i stepene: a); b).
a) Koristimo formulu za pretvaranje stupnjeva u radijane
![]()
Zamijenimo navedenu vrijednost u njega.
b) Primijenite formulu za pretvaranje radijana u stupnjeve
![]()
Izvršimo zamjenu ![]() .
.
Odgovori. a) ; b).
Problem broj 2... Izračunajte: a); b).
a) Pošto je ugao daleko iznad tabelarnog, smanjićemo ga oduzimanjem perioda sinusa. Jer ugao je naznačen u radijanima, tada će se period smatrati kao.
b) U ovom slučaju situacija je slična. Pošto je ugao naznačen u stepenima, onda će se period tangente smatrati kao.
Rezultirajući ugao, iako manji od perioda, je veći, što znači da se više ne odnosi na glavni, već na prošireni dio tabele. Da ne bismo još jednom trenirali našu memoriju pamćenjem proširene tablice vrijednosti trig funkcije, ponovo oduzimamo period tangente:
Iskoristili smo neparnost tangentne funkcije.
Odgovori. a) 1; b).
Problem broj 3... Izračunati ![]() , ako .
, ako .
Dovodimo cijeli izraz na tangente, dijeleći brojilac i imenilac razlomka sa. Istovremeno, toga se ne možemo bojati, jer u ovom slučaju tangentna vrijednost ne bi postojala.
Problem broj 4... Pojednostavite izraz.
Navedeni izrazi se konvertuju pomoću formula za pretvaranje. Samo što su neobično napisane pomoću stepeni. Prvi izraz je općenito broj. Pojednostavimo redom sve trig funkcije:
Jer , tada se funkcija mijenja u kofunkciju, tj. na kotangens, a ugao pada u drugu četvrtinu, u kojoj prvobitna tangenta ima negativan predznak.

Iz istih razloga kao u prethodnom izrazu, funkcija se mijenja u kofunkciju, tj. na kotangensu, a ugao pada u prvu četvrtinu, u kojoj izvorna tangenta ima pozitivan predznak.
Zamenimo sve u pojednostavljeni izraz:
Problem broj 5... Pojednostavite izraz.
Zapišimo tangentu dvostrukog ugla prema odgovarajućoj formuli i pojednostavimo izraz:
Posljednji identitet je jedna od univerzalnih zamjenskih formula za kosinus.
Problem broj 6... Izračunati.
Glavna stvar je ne napraviti standardnu grešku i ne dati odgovor da je izraz jednak. Nemoguće je koristiti glavno svojstvo arktangensa sve dok pored njega postoji množitelj u obliku dva. Da bismo ga se riješili, pišemo izraz prema formuli za tangentu dvostrukog ugla, dok ga tretiramo kao običan argument.
![]()
Sada možete primijeniti glavno svojstvo arktangensa, zapamtite da nema ograničenja za njegov numerički rezultat.
Problem broj 7... Riješite jednačinu.
Prilikom odlučivanja frakciona jednačina, što je jednako nuli, uvijek je naznačeno da je brojilac nula, ali imenilac nije, jer Ne možete dijeliti sa nulom.

Prva jednadžba je poseban slučaj najjednostavnija jednačina, koja se rješava pomoću trigonometrijskog kruga. Zapamtite ovo rješenje i sami. Druga nejednakost je riješena kao najjednostavnija jednadžba prema općoj formuli za korijene tangente, ali je samo uz oznaku znaka nejednaka.

Kao što možete vidjeti, jedna porodica korijena isključuje drugu porodicu korijena koji ne zadovoljavaju jednačinu potpuno istog oblika. One. nema korijena.
Odgovori. Nema korijena.
Problem broj 8... Riješite jednačinu.
Odmah napominjemo da možete izvaditi zajednički faktor i to učiniti:
Jednačina je svedena na jedan od standardnih oblika, kada je proizvod više faktora jednak nuli. Već znamo da je u ovom slučaju ili jedan od njih nula, ili drugi, ili treći. Zapišimo ovo u obliku skupa jednadžbi:

Prve dvije jednadžbe su posebni slučajevi najjednostavnijih, sa sličnim jednačinama smo se već susreli mnogo puta, pa ćemo odmah naznačiti njihova rješenja. Treća jednadžba se reducira na jednu funkciju koristeći sinusnu formulu dvostrukog ugla.

Riješimo posljednju jednačinu posebno:
![]()
Ova jednadžba nema korijen, jer vrijednost sinusa ne može izaći izvan granica ![]() .
.
Dakle, rješenje su samo prve dvije porodice korijena, oni se mogu kombinovati u jednu, što se lako može prikazati na trigonometrijskom krugu:
 |
Ovo je porodica svih polovina, tj.
Pređimo na rješavanje trigonometrijskih nejednačina. Prvo ćemo analizirati pristup rješavanju primjera bez korištenja formula za opća rješenja, već pomoću trigonometrijskog kruga.
Problem broj 9... Riješite nejednakost.
Nacrtajte na trigonometrijsku kružnicu pomoćnu liniju koja odgovara vrijednosti sinusa jednakoj i pokažite interval uglova koji zadovoljavaju nejednakost.
 |
Vrlo je važno razumjeti kako tačno označiti rezultirajući raspon uglova, tj. šta je njegov početak, a šta kraj. Početak intervala će biti ugao koji odgovara tački u koju ćemo ući na samom početku intervala, ako se krećemo suprotno od kazaljke na satu. U našem slučaju, ovo je tačka koja je sa leve strane, jer krećući se u smjeru suprotnom od kazaljke na satu i prolazeći pravu tačku, mi, naprotiv, ostavljamo traženi raspon uglova. Tačka na desnoj strani će stoga odgovarati kraju praznine.
Sada je potrebno razumjeti vrijednosti uglova početka i kraja našeg intervala rješenja nejednakosti. Tipična greška je da se odmah naznači da desna tačka odgovara uglu, levo i da se odgovori. Ovo nije istina! Napominjemo da smo upravo naveli razmak koji odgovara gornjem dijelu kruga, iako nas zanima donji, drugim riječima, pobrkali smo početak i kraj intervala potrebnih rješenja.
Da bi interval započeo u uglu desne tačke i završio u uglu lijeve tačke, prvi navedeni ugao mora biti manji od drugog. Da bismo to učinili, morat ćemo izmjeriti ugao desne tačke u negativnom smjeru reference, tj. u smeru kazaljke na satu i biće jednako. Zatim, počevši od njega u pozitivnom smjeru u smjeru kazaljke na satu, doći ćemo do desne točke nakon lijeve točke i dobiti vrijednost ugla za nju. Sada je početak intervala uglova manji od kraja i možemo napisati interval rješenja bez uzimanja u obzir perioda:
Uzimajući u obzir da će se takvi intervali ponavljati beskonačan broj puta nakon bilo kojeg cijelog broja zavoja, dobivamo opće rješenje uzimajući u obzir sinusni period:
Stavljamo zagrade zbog činjenice da je nejednakost stroga, a na kružnici izvlačimo tačke koje odgovaraju krajevima intervala.
Uporedite svoj odgovor sa općom formulom rješenja koju smo predstavili na predavanju.
Odgovori. ![]() .
.
Ova metoda je dobra za razumijevanje odakle dolaze formule za opšta rješenja najjednostavnijih trigonskih jednačina. Osim toga, korisno je za one koji su previše lijeni da nauče sve ove glomazne formule. Međutim, sama metoda također nije laka, odaberite koji vam pristup rješenju najviše odgovara.
Za rješavanje trigonometrijskih nejednakosti možete koristiti i grafove funkcija na kojima je konstruirana pomoćna linija na sličan način kao što je prikazano pomoću jediničnog kruga. Ako ste zainteresirani, pokušajte sami shvatiti ovaj pristup rješenju. U nastavku ćemo koristiti opće formule za rješavanje najjednostavnijih trigonometrijskih nejednačina.
Problem broj 10... Riješite nejednakost.
Koristimo formulu za opće rješenje, uzimajući u obzir da nejednakost nije stroga:
U našem slučaju dobijamo:
Odgovori. ![]()
Problem broj 11... Riješite nejednakost.
Upotrijebimo opću formulu rješenja za odgovarajuću striktno nejednakost:
Odgovori. ![]() .
.
Problem broj 12... Riješite nejednačine: a); b).
U ovim nejednačinama nema potrebe žuriti s korištenjem formula za opća rješenja ili trigonometrijskog kruga, dovoljno je samo zapamtiti raspon vrijednosti sinusa i kosinusa.
a) Od ![]() , onda je nejednakost besmislena. Dakle, nema rješenja.
, onda je nejednakost besmislena. Dakle, nema rješenja.
b) Zato što slično, sinus bilo kojeg argumenta uvijek zadovoljava nejednakost specificiranu u uvjetu. Dakle, sve realne vrijednosti argumenta zadovoljavaju nejednakost.
Odgovori. a) nema rješenja; b).
Zadatak 13... Riješite nejednakost ![]() .
.
Rješavanje najjednostavnijih trigonometrijskih jednadžbi
Za početak, prisjetimo se formula za rješavanje najjednostavnijih trigonometrijskih jednadžbi.
- $ sinx = a $
- $ cosx = a $
- $ tgx = a $
- $ ctgx = a $
Rješenje najjednostavnijih trigonometrijskih nejednačina.
Da bismo riješili najjednostavnije trigonometrijske nejednačine, prvo trebamo riješiti odgovarajuću jednadžbu, a zatim pomoću trigonometrijskog kruga pronaći rješenje nejednačine. Razmotrimo rješenja najjednostavnijih trigonometrijskih nejednačina na primjerima.
Primjer 1
$ sinx \ ge \ frac (1) (2) $
Nađimo rješenje trigonometrijske nejednakosti $ sinx = \ frac (1) (2) $
\ \
Slika 1. Rješenje nejednakosti $ sinx \ ge \ frac (1) (2) $.
Kako nejednakost ima predznak "veće ili jednako", rješenje leži na gornjem luku kružnice (u odnosu na rješenje jednadžbe).
Odgovor: $ \ lijevo [\ frac (\ pi) (6) +2 \ pi n, \ frac (5 \ pi) (6) +2 \ pi n \ desno] $.
Primjer 2
Pronađite rješenje trigonometrijske nejednakosti $ cosx = \ frac (\ sqrt (3)) (2) $
\ \
Rješenje označavamo na trigonometrijskom krugu
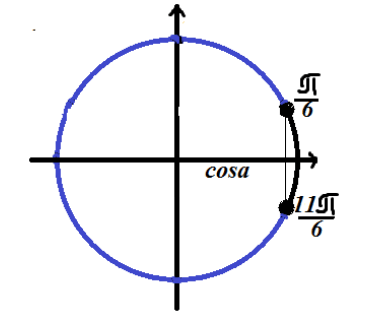
Kako nejednakost ima predznak manji od, rješenje leži na luku kružnice koja se nalazi lijevo (u odnosu na rješenje jednadžbe).
Odgovor: $ \ lijevo (\ frac (\ pi) (6) +2 \ pi n, \ frac (11 \ pi) (6) +2 \ pi n \ desno) $.
Primjer 3
$ tgx \ le \ frac (\ sqrt (3)) (3) $
Nađimo rješenje trigonometrijske nejednakosti $ tgx = \ frac (\ sqrt (3)) (3) $
\ \
Ovdje nam je također potrebna domena. Kao što se sjećamo, tangentna funkcija $ x \ ne \ frac (\ pi) (2) + \ pi n, n \ u Z $
Rješenje označavamo na trigonometrijskom krugu
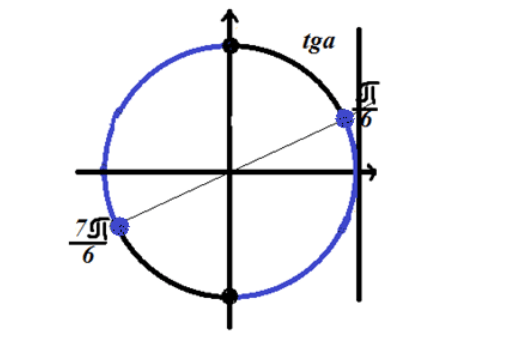
Slika 3. Rješenje nejednakosti $ tgx \ le \ frac (\ sqrt (3)) (3) $.
Budući da nejednačina ima predznak manji ili jednak, rješenje leži na kružnim lukovima označenim plavom bojom na slici 3.
Odgovor: $ \ \ lijevo (- \ frac (\ pi) (2) +2 \ pi n \ desno., \ lijevo \ frac (\ pi) (6) +2 \ pi n \ desno] \ čaša \ lijevo (\ frac (\ pi) (2) +2 \ pi n, \ desno. \ lijevo. \ frac (7 \ pi) (6) +2 \ pi n \ desno] $
Primjer 4
Pronađite rješenje trigonometrijske nejednakosti $ ctgx = \ sqrt (3) $
\ \
Ovdje nam je također potrebna domena. Kao što se sjećamo, tangentna funkcija $ x \ ne \ pi n, n \ u Z $
Rješenje označavamo na trigonometrijskom krugu

Slika 4. Rješenje nejednakosti $ ctgx \ le \ sqrt (3) $.
Budući da nejednačina ima predznak "veće od", rješenje leži na kružnim lukovima označenim plavom bojom na slici 4.
Odgovor: $ \ \ lijevo (2 \ pi n, \ frac (\ pi) (6) +2 \ pi n \ desno) \ čaša \ lijevo (\ pi +2 \ pi n, \ frac (7 \ pi) ( 6) +2 \ pi n \ desno) $








