Ako problem zahtijeva potpuno proučavanje funkcije f (x) = x 2 4 x 2 - 1 sa konstrukcijom njenog grafa, onda ćemo ovaj princip detaljno razmotriti.
Da biste riješili problem ovog tipa, trebali biste koristiti svojstva i grafove osnovnih elementarnih funkcija. Algoritam istraživanja uključuje sljedeće korake:
Pronalaženje domene definicije
S obzirom da se istraživanje provodi u domenu definicije funkcije, potrebno je krenuti s ovim korakom.
Primjer 1
Iza ovaj primjer uključuje pronalaženje nula nazivnika kako bi se isključile iz ODZ-a.
4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞ ; - 1 2 ∪ - 1 2 ; 1 2 ∪ 1 2 ; +∞
Kao rezultat, možete dobiti korijene, logaritme i tako dalje. Tada se ODZ može tražiti korijen parnog stepena tipa g (x) 4 po nejednakosti g (x) ≥ 0, za logaritam log a g (x) po nejednakosti g (x) > 0.
Proučavanje granica ODZ-a i pronalaženje vertikalnih asimptota
Postoje vertikalne asimptote na granicama funkcije, kada su jednostrane granice u takvim tačkama beskonačne.
Primjer 2
Na primjer, razmotrite granične točke jednake x = ± 1 2.
Zatim je potrebno proučiti funkciju da bi se pronašla jednostrana granica. Tada dobijamo: lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (- 2) · - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) 2 = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0 ) 2 = + ∞
Ovo pokazuje da su jednostrane granice beskonačne, što znači da su prave linije x = ± 1 2 vertikalne asimptote grafa.
Proučavanje funkcije i da li je parna ili neparna
Kada je uslov y (- x) = y (x) zadovoljen, funkcija se smatra parnom. Ovo sugerira da se graf nalazi simetrično u odnosu na Oy. Kada je uslov y (- x) = - y (x) zadovoljen, funkcija se smatra neparnom. To znači da je simetrija relativna u odnosu na ishodište koordinata. Ako barem jedna nejednakost nije zadovoljena, dobijamo funkciju općeg oblika.
Jednakost y (- x) = y (x) ukazuje da je funkcija parna. Prilikom konstruisanja potrebno je uzeti u obzir da će postojati simetrija u odnosu na Oy.
Za rješavanje nejednakosti koriste se intervali povećanja i opadanja sa uslovima f " (x) ≥ 0 i f " (x) ≤ 0, respektivno.
Definicija 1
Stacionarne tačke- to su tačke koje pretvaraju izvod na nulu.
Kritične tačke - to su unutrašnje tačke iz domena definicije u kojima je derivacija funkcije jednaka nuli ili ne postoji.
Prilikom donošenja odluke potrebno je uzeti u obzir sljedeće napomene:
- za postojeće intervale rastućih i opadajućih nejednačina oblika f" (x) > 0, kritične tačke nisu uključene u rješenje;
- tačke u kojima je funkcija definisana bez konačnog izvoda moraju biti uključene u intervale povećanja i smanjenja (na primer, y = x 3, gde tačka x = 0 čini funkciju definisanom, izvod ima vrednost beskonačnosti u ovom tačka, y " = 1 3 x 2 3, y "(0) = 1 0 = ∞, x = 0 je uključeno u rastući interval);
- Kako bi se izbjegle nesuglasice, preporučuje se korištenje matematičke literature koju preporučuje Ministarstvo prosvjete.
Uključivanje kritičnih tačaka u intervale rasta i opadanja ako zadovoljavaju domen definicije funkcije.
Definicija 2
Za određivanje intervala povećanja i smanjenja funkcije, potrebno je pronaći:
- derivat;
- kritične tačke;
- podijeliti domenu definicije na intervale koristeći kritične tačke;
- odrediti predznak izvoda na svakom od intervala, gdje je + povećanje, a - smanjenje.
Primjer 3
Pronađite izvod na domeni definicije f " (x) = x 2 " (4 x 2 - 1) - x 2 4 x 2 - 1 " (4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .
Rješenje
Za rješavanje potrebno je:
- pronađite stacionarne tačke, ovaj primjer ima x = 0;
- pronađite nule nazivnika, primjer uzima vrijednost nula na x = ± 1 2.
Postavljamo tačke na brojevnu pravu da odredimo izvod na svakom intervalu. Da biste to učinili, dovoljno je uzeti bilo koju tačku iz intervala i izvršiti proračun. Ako je rezultat pozitivan, na grafu prikazujemo +, što znači da funkcija raste, a - znači da je opadajuća.
Na primjer, f " (- 1) = - 2 · (- 1) 4 - 1 2 - 1 2 = 2 9 > 0, što znači da prvi interval lijevo ima znak +. Razmotrite brojevnu pravu.
odgovor:
- funkcija raste na intervalu - ∞; - 1 2 i (- 1 2 ; 0 ] ;
- dolazi do smanjenja intervala [ 0 ; 1 2) i 1 2 ; + ∞ .
Na dijagramu, koristeći + i -, prikazani su pozitivnost i negativnost funkcije, a strelice pokazuju smanjenje i povećanje.
Ekstremne tačke funkcije su tačke u kojima je funkcija definisana i kroz koje derivacija menja predznak.
Primjer 4
Ako uzmemo u obzir primjer gdje je x = 0, tada je vrijednost funkcije u njemu jednaka f (0) = 0 2 4 · 0 2 - 1 = 0. Kada se predznak derivacije promijeni sa + na - i prođe kroz tačku x = 0, tada se tačka s koordinatama (0; 0) smatra maksimalnom tačkom. Kada se predznak promijeni sa - na +, dobijamo minimalnu tačku.
Konveksnost i konkavnost se određuju rješavanjem nejednačina oblika f "" (x) ≥ 0 i f "" (x) ≤ 0. Manje se koristi naziv konveksnost prema dolje umjesto konkavnost i konveksnost prema gore umjesto konveksnost.
Definicija 3
Za određivanje intervala konkavnosti i konveksnosti potrebno:
- naći drugi izvod;
- naći nule druge derivacijske funkcije;
- podijeliti područje definicije na intervale sa tačkama koje se pojavljuju;
- odrediti predznak intervala.
Primjer 5
Nađite drugi izvod iz domena definicije.
Rješenje
f "" (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) " (4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 " (4 x 2 - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3
Pronalazimo nule brojioca i nazivnika, pri čemu u našem primjeru imamo da su nule nazivnika x = ± 1 2
Sada trebate nacrtati tačke na brojevnoj pravoj i odrediti predznak drugog izvoda iz svakog intervala. Shvatili smo to

odgovor:
- funkcija je konveksna iz intervala - 1 2 ; 12 ;
- funkcija je konkavna iz intervala - ∞ ; - 1 2 i 1 2; + ∞ .
Definicija 4
Prevojna tačka– ovo je tačka oblika x 0 ; f (x 0) . Kada ima tangentu na graf funkcije, onda kada prođe kroz x 0, funkcija mijenja predznak u suprotan.
Drugim riječima, ovo je tačka kroz koju prolazi drugi izvod i mijenja predznak, a u samim tačkama jednak je nuli ili ne postoji. Sve tačke se smatraju domenom funkcije.
U primjeru je bilo jasno da nema pregibnih tačaka, jer drugi izvod mijenja predznak prolazeći kroz tačke x = ± 1 2. Oni, pak, nisu uključeni u opseg definicije.
Pronalaženje horizontalnih i kosih asimptota
Kada definišete funkciju u beskonačnosti, morate tražiti horizontalne i kose asimptote.
Definicija 5
Kose asimptote prikazani su pravim linijama, dato jednačinom y = k x + b, gdje je k = lim x → ∞ f (x) x i b = lim x → ∞ f (x) - k x.
Za k = 0 i b nije jednako beskonačnosti, nalazimo da kosa asimptota postaje horizontalno.
Drugim riječima, asimptote se smatraju linijama kojima se graf funkcije približava beskonačno. Ovo olakšava brzu konstrukciju grafa funkcije.
Ako nema asimptota, ali je funkcija definirana na obje beskonačnosti, potrebno je izračunati granicu funkcije na tim beskonačnostima kako bi se razumjelo kako će se ponašati graf funkcije.
Primjer 6
Razmotrimo kao primjer to
k = lim x → ∞ f (x) x = lim x → ∞ x 2 4 x 2 - 1 x = 0 b = lim x → ∞ (f (x) - k x) = lim x → ∞ x 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4
je horizontalna asimptota. Nakon pregleda funkcije, možete početi da je konstruišete.
Izračunavanje vrijednosti funkcije u međutočkama
Da bi graf bio precizniji, preporučuje se pronaći nekoliko vrijednosti funkcije u srednjim točkama.
Primjer 7
Iz primjera koji smo razmatrali potrebno je pronaći vrijednosti funkcije u tačkama x = - 2, x = - 1, x = - 3 4, x = - 1 4. Pošto je funkcija parna, dobijamo da se vrednosti poklapaju sa vrednostima u ovim tačkama, odnosno dobijamo x = 2, x = 1, x = 3 4, x = 1 4.
Hajde da napišemo i rešimo:
F (- 2) = f (2) = 2 2 4 2 2 - 1 = 4 15 ≈ 0, 27 f (- 1) - f (1) = 1 2 4 1 2 - 1 = 1 3 ≈ 0 , 33 f - 3 4 = f 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 f - 1 4 = f 1 4 = 1 4 2 4 1 4 2 - 1 = - 1 12 ≈ - 0,08
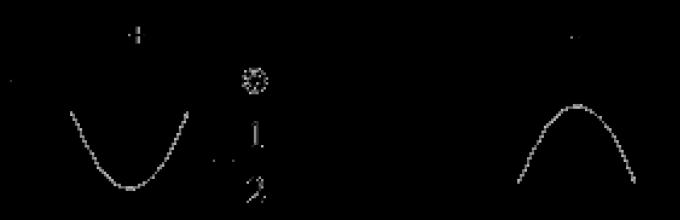
Da bi se odredili maksimumi i minimumi funkcije, tačke pregiba i međutačke, potrebno je konstruisati asimptote. Za zgodna oznaka bilježe se intervali povećanja, smanjenja, konveksnosti, konkavnosti. Pogledajmo sliku ispod.

Kroz označene tačke potrebno je povući linije grafa, što će vam omogućiti da pristupite asimptoti prateći strelice.

Ovim se završava potpuno istraživanje funkcije. Postoje slučajevi konstruisanja nekih elementarnih funkcija za koje se koriste geometrijske transformacije.
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter
Prilikom crtanja grafova funkcija korisno je pridržavati se sljedećeg plana:
1. Pronađite područje definicije funkcije i odredite točke diskontinuiteta, ako ih ima.
2. Odredite da li je funkcija parna ili neparna ili nijedna. Ako je funkcija parna ili neparna, dovoljno je uzeti u obzir njene vrijednosti na x>0, a zatim simetrično u odnosu na OY os ili ishodište koordinata, vratite ga za vrijednosti x<0 .
3. Ispitajte funkciju za periodičnost. Ako je funkcija periodična, dovoljno je razmotriti je na jednom periodu.
4. Pronađite točke presjeka grafa funkcije sa koordinatnim osama (ako je moguće)
5. Provesti studiju funkcije na ekstremumu i pronaći intervale povećanja i smanjenja funkcije.
6. Naći prevojne tačke krivulje i intervale konveksnosti i konkavnosti funkcije.
7. Pronađite asimptote grafa funkcije.
8. Koristeći rezultate koraka 1-7, konstruirajte graf funkcije. Ponekad se pronađe nekoliko dodatnih tačaka za veću preciznost; njihove koordinate se izračunavaju pomoću jednačine krive.
Primjer. Funkcija istraživanja y=x 3 -3x i napravi graf.
1) Funkcija je definirana na intervalu (-∞; +∞). Nema prelomnih tačaka.
2) Funkcija je neparna, jer f(-x) = -x 3 -3(-x) = -x 3 +3x = -f(x), dakle, simetričan je u odnosu na ishodište.
3) Funkcija nije periodična.
4) Tačke preseka grafika sa koordinatnim osa: x 3 -3x=0, x = , x = -, x = 0, one. graf funkcije siječe koordinatne osi u tačkama: ( ; 0 ), (0; 0 ), (-; 0 ).
5) Pronađite moguće tačke ekstrema: y′ = 3x 2 -3; 3x 2 -3=0; x =-1; x = 1. Područje definicije funkcije podijelit će se na intervale: (-∞; -1), (-1; 1), (1; +∞). Nađimo predznake derivacije u svakom rezultujućem intervalu:
Na intervalu (-∞; -1) y′>0 – funkcija se povećava
Na intervalu (-1; 1) y′<0 – funkcija se smanjuje
Na intervalu (1; +∞) y′>0 – funkcija se povećava. Dot x =-1 – maksimalni bod; x = 1 – minimalni bod.
6) Pronađite prevojne tačke: y′′ = 6x; 6x = 0; x = 0. Dot x = 0 dijeli domenu definicije na intervale (-∞; 0), (0; +∞). Nađimo predznake druge derivacije u svakom rezultujućem intervalu:
Na intervalu (-∞;0) y′′<0 – funkcija je konveksna
Na intervalu (0; +∞) y′′>0 – funkcija je konkavna. x = 0– tačka pregiba.
7) Graf nema asimptote
8) Nacrtajmo funkciju:
Primjer. Istražite funkciju i izgradite njen graf.
1) Područje definicije funkcije su intervali (-¥; -1) È (-1; 1) È (1; ¥). Raspon vrijednosti ove funkcije je interval (-¥; ¥).
Prelomne tačke funkcije su tačke x = 1, x = -1.
2) Funkcija je neparna, jer .
3) Funkcija nije periodična.
4) Grafikon siječe koordinatne ose u tački (0; 0).
5) Pronađite kritične tačke.
Kritične tačke: x = 0; x = -; x = ; x = -1; x = 1.
Naći intervale rastuće i opadajuće funkcije. Da bismo to učinili, određujemo predznake derivacije funkcije na intervalima.
-¥ < x< -, y¢> 0, funkcija se povećava
-< x < -1, y¢ < 0, функция убывает
1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x < , y¢ < 0, функция убывает
< x < ¥, y¢ > 0, funkcija se povećava
Jasno je da je poenta X= -je maksimalna tačka i tačka X= je minimalna tačka. Vrijednosti funkcije u ovim tačkama jednake su 3/2 i -3/2, respektivno.
6) Pronađite drugi izvod funkcije
Jednačina kose asimptote: y = x.
8) Napravimo graf funkcije.
Ova lekcija pokriva temu "Istraživanje funkcije i povezanih problema." Ova lekcija pokriva grafičke funkcije pomoću derivata. Funkcija se proučava, konstruiše se njen graf i rešava niz povezanih problema.
Tema: Derivat
Lekcija: Istraživanje funkcijei srodnim zadacima
Potrebno je proučiti ovu funkciju, konstruisati graf, pronaći intervale monotonosti, maksimume, minimume i koji problemi prate znanja o ovoj funkciji.
Prvo, hajde da u potpunosti iskoristimo informacije koje pruža funkcija bez izvoda.
1. Pronađite intervale konstantnog predznaka funkcije i konstruirajte skicu grafa funkcije:
1) Hajde da pronađemo.
2) Korijeni funkcije: , odavde
3) Intervali konstantnog predznaka funkcije (vidi sliku 1):

Rice. 1. Intervali konstantnog predznaka funkcije.
Sada znamo da je u intervalu i graf iznad X-ose, u intervalu - ispod X-ose.
2. Napravimo graf u blizini svakog korijena (vidi sliku 2).

Rice. 2. Grafikon funkcije u blizini korijena.
3. Konstruirati graf funkcije u blizini svake tačke diskontinuiteta u domeni definicije. Domen definicije se prekida u tački . Ako je vrijednost blizu tačke, tada vrijednost funkcije teži (vidi sliku 3).

Rice. 3. Grafikon funkcije u blizini tačke diskontinuiteta.
4. Odredimo kako se graf ponaša u blizini tačaka u beskonačnosti:
Hajde da to napišemo koristeći ograničenja
![]() . Važno je da se za vrlo velike vrijednosti funkcija gotovo ne razlikuje od jedinice.
. Važno je da se za vrlo velike vrijednosti funkcija gotovo ne razlikuje od jedinice.
Nađimo derivaciju, intervale njenog konstantnog predznaka i to će biti intervali monotonosti za funkciju, pronaći one tačke u kojima je izvod jednak nuli i saznati gdje je tačka maksimuma, a gdje minimalna tačka.
Odavde, . Ove tačke su unutrašnje tačke domena definicije. Hajde da saznamo koji je predznak derivacije na intervalima, i koja od ovih tačaka je tačka maksimuma, a koja tačka minimuma (vidi sliku 4).

Rice. 4. Intervali konstantnog predznaka derivacije.
Od sl. 4 vidi se da je tačka minimalna tačka, tačka maksimalna tačka. Vrijednost funkcije u točki je . Vrijednost funkcije u tački je 4. Sada napravimo graf funkcije (vidi sliku 5).

Rice. 5. Grafikon funkcija.
Tako smo gradili graf funkcije. Hajde da to opišemo. Zapišimo intervale u kojima funkcija monotono opada: , su oni intervali u kojima je izvod negativan. Funkcija raste monotono na intervalima i . - minimalni bod, - maksimalni bod.
Odrediti broj korijena jednadžbe u zavisnosti od vrijednosti parametara.
1. Konstruirajte graf funkcije. Grafikon ove funkcije je prikazan iznad (vidi sliku 5).
2. Secirajte graf sa familijom pravih linija i zapišite odgovor (vidi sliku 6).

Rice. 6. Presjek grafa funkcije s pravim linijama.
1) Kada - jedno rešenje.
2) Za - dva rješenja.
3) Kada - tri rješenja.
4) Kada - dva rješenja.
5) Kada - tri rješenja.
6) Kada - dva rješenja.
7) Kada - jedno rešenje.
Time smo riješili jedan od važnih problema, odnosno pronalaženje broja rješenja jednadžbe u zavisnosti od parametra . Mogu postojati različiti posebni slučajevi, na primjer, u kojima će postojati jedno rješenje, ili dva rješenja, ili tri rješenja. Imajte na umu da su ovi posebni slučajevi, svi odgovori na ove posebne slučajeve sadržani u općem odgovoru.
1. Algebra i početak analize, 10. ocjena (iz dva dijela). Tutorial za obrazovne institucije (nivo profila) ed. A. G. Mordkovich. -M.: Mnemosyne, 2009.
2. Algebra i početak analize, 10. ocjena (iz dva dijela). Problematika za obrazovne ustanove (profilni nivo), ur. A. G. Mordkovich. -M.: Mnemosyne, 2007.
3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebra i računica za 10. razred ( tutorial za učenike škola i odeljenja sa dubinska studija matematika).-M.: Obrazovanje, 1996.
4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Dubinski studij algebre i matematičke analize.-M.: Obrazovanje, 1997.
5. Zbirka zadataka iz matematike za kandidate za visokoškolske ustanove (priredio M.I. Skanavi) - M.: Viša škola, 1992.
6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebarski simulator.-K.: A.S.K., 1997.
7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina algebra i počeci analize. 8-11 razred: Priručnik za škole i odeljenja sa detaljnim proučavanjem matematike (didaktički materijali) - M.: Drfa, 2002.
8. Sahakyan S.M., Goldman A.M., Denisov D.V. Problemi iz algebre i principi analize (priručnik za učenike 10-11 razreda opšteobrazovnih ustanova) - M.: Prosveščenie, 2003.
9. Karp A.P. Zbirka zadataka iz algebre i principi analize: udžbenik. dodatak za 10-11 razred. sa dubinom studirao Matematika.-M.: Obrazovanje, 2006.
10. Glazer G.I. Istorija matematike u školi. 9-10 razred (priručnik za nastavnike).-M.: Prosveta, 1983
Dodatni web resursi
2. Portal Prirodne nauke ().
Napravite ga kod kuće
br. 45.7, 45.10 (Algebra i počeci analize, 10. razred (u dva dijela). Zadatak za opšteobrazovne ustanove (profilni nivo) priredio A. G. Mordkovich. - M.: Mnemosyne, 2007.)