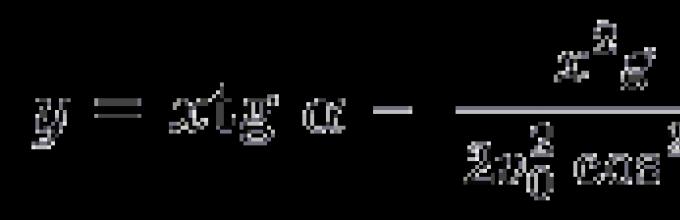Matematičko modeliranje

1. Šta je matematičko modeliranje?

Od sredine 20. veka. Matematičke metode i kompjuteri počeli su da se široko koriste u različitim oblastima ljudske aktivnosti. Pojavile su se nove discipline kao što su „matematička ekonomija”, „matematička hemija”, „matematička lingvistika” itd., koje proučavaju matematičke modele relevantnih objekata i pojava, kao i metode za proučavanje ovih modela.

Matematički model je približan opis bilo koje klase pojava ili objekata stvarnog svijeta na jeziku matematike. Glavna svrha modeliranja je istraživanje ovih objekata i predviđanje rezultata budućih promatranja. Međutim, modeliranje je i metoda razumijevanja svijeta oko nas, omogućavajući njegovu kontrolu.

Matematičko modeliranje i povezani kompjuterski eksperimenti su neophodni u slučajevima kada je eksperiment u punoj veličini nemoguć ili težak iz ovog ili onog razloga. Na primjer, nemoguće je postaviti prirodni eksperiment u historiji kako bi se provjerilo “šta bi se dogodilo da...” Nemoguće je provjeriti ispravnost jedne ili druge kosmološke teorije. Moguće je, ali malo vjerovatno da će biti razumno, eksperimentirati sa širenjem bolesti, kao što je kuga, ili izvesti nuklearnu eksploziju kako bi se proučile njene posljedice. Međutim, sve se to može uraditi na računaru tako što se prvo konstruišu matematički modeli fenomena koji se proučavaju.

2. Glavne faze matematičkog modeliranja

1) Izgradnja modela. U ovoj fazi precizira se neki „nematematički“ objekt – prirodni fenomen, dizajn, ekonomski plan, proizvodni proces itd. U ovom slučaju, po pravilu, jasan opis situacije je težak. Prvo se identifikuju glavne karakteristike fenomena i veze između njih na kvalitativnom nivou. Zatim se pronađene kvalitativne zavisnosti formulišu jezikom matematike, odnosno gradi se matematički model. Ovo je najteža faza modeliranja.

2) Rješavanje matematičkog problema do kojeg vodi model. U ovoj fazi se velika pažnja poklanja razvoju algoritama i numeričkih metoda za rješavanje problema na računaru, uz pomoć kojih se rezultat može pronaći sa potrebnom tačnošću iu prihvatljivom vremenu.

3) Interpretacija dobijenih posledica iz matematičkog modela. Posljedice koje proizilaze iz modela na jeziku matematike tumače se jezikom prihvaćenim u ovoj oblasti.

4) Provjera adekvatnosti modela. U ovoj fazi se utvrđuje da li se eksperimentalni rezultati slažu s teorijskim posljedicama modela u određenoj preciznosti.

5) Modifikacija modela. U ovoj fazi ili se model komplikuje kako bi bio adekvatniji realnosti, ili se pojednostavljuje kako bi se postiglo praktično prihvatljivo rješenje.

3. Klasifikacija modela

Modeli se mogu klasifikovati prema različitim kriterijumima. Na primjer, prema prirodi problema koji se rješavaju, modeli se mogu podijeliti na funkcionalne i strukturalne. U prvom slučaju, kvantitativno se izražavaju sve veličine koje karakteriziraju pojavu ili predmet. Štaviše, neke od njih se smatraju nezavisnim varijablama, dok se druge smatraju funkcijama ovih veličina. Matematički model je obično sistem jednačina različitih tipova (diferencijalni, algebarski, itd.) koji uspostavljaju kvantitativne odnose između veličina koje se razmatraju. U drugom slučaju, model karakterizira strukturu složenog objekta koji se sastoji od pojedinačnih dijelova, između kojih postoje određene veze. Obično se ove veze ne mogu kvantificirati. Za konstruiranje takvih modela zgodno je koristiti teoriju grafova. Graf je matematički objekat koji predstavlja skup tačaka (vrhova) na ravni ili u prostoru, od kojih su neke povezane linijama (ivicama).

Na osnovu prirode početnih podataka i rezultata, modeli predviđanja se mogu podijeliti na determinističke i vjerovatno-statističke. Modeli prvog tipa daju određena, nedvosmislena predviđanja. Modeli drugog tipa zasnivaju se na statističkim informacijama, a predviđanja dobijena uz njihovu pomoć su vjerovatnoće.

4. Primjeri matematičkih modela

1) Problemi o kretanju projektila.

Razmotrite sljedeći problem mehanike.

Projektil se lansira sa Zemlje početnom brzinom v 0 = 30 m/s pod uglom a = 45° prema njenoj površini; potrebno je pronaći putanju njegovog kretanja i udaljenost S između početne i krajnje tačke ove putanje.

Zatim, kao što je poznato iz školskog predmeta fizike, kretanje projektila opisuje se formulama:

gdje je t vrijeme, g = 10 m/s 2 je ubrzanje gravitacije. Ove formule daju matematički model problema. Izražavajući t kroz x iz prve jednačine i zamjenom je u drugu, dobijamo jednačinu za putanju projektila:

Ova kriva (parabola) siječe x osu u dvije tačke: x 1 = 0 (početak putanje) i (mesto gde je projektil pao). Zamjenom datih vrijednosti v0 i a u rezultirajuće formule, dobijamo

odgovor: y = x – 90x 2, S = 90 m.

Imajte na umu da su prilikom konstruiranja ovog modela korištene brojne pretpostavke: na primjer, pretpostavlja se da je Zemlja ravna, a zrak i rotacija Zemlje ne utiču na kretanje projektila.

2) Problem sa rezervoarom sa najmanjom površinom.

Potrebno je pronaći visinu h 0 i poluprečnik r 0 limenog rezervoara zapremine V = 30 m 3, koji ima oblik zatvorenog kružnog cilindra, pri čemu je njegova površina S minimalna (u ovom slučaju najmanja količina kalaja će se koristiti za njegovu proizvodnju).

Napišimo sljedeće formule za volumen i površinu cilindra visine h i polumjera r:

V = p r 2 h, S = 2p r(r + h).

Izražavajući h kroz r i V iz prve formule i zamjenjujući rezultirajući izraz u drugu, dobivamo:

Dakle, sa matematičke tačke gledišta, problem se svodi na određivanje vrijednosti r pri kojoj funkcija S(r) dostiže svoj minimum. Nađimo one vrijednosti r 0 za koje je izvod

ide na nulu: Možete provjeriti da li drugi izvod funkcije S(r) mijenja predznak iz minusa u plus kada argument r prolazi kroz tačku r 0 . Prema tome, u tački r0 funkcija S(r) ima minimum. Odgovarajuća vrijednost je h 0 = 2r 0 . Zamjenom date vrijednosti V u izraz za r 0 i h 0, dobijamo željeni polumjer i visina

3) Transportni problem.

Grad ima dva magacina brašna i dvije pekare. Dnevno se iz prvog skladišta transportuje 50 tona brašna, a iz drugog u fabrike 70 tona, od čega u prvo 40 tona, a u drugo 80 tona.

Označimo sa a ij je trošak transporta 1 tone brašna od i-og skladišta do j-tog pogona (i, j = 1,2). Neka

a 11 = 1,2 rublje, a 12 = 1,6 rubalja, a 21 = 0,8 rub., a 22 = 1 rub.

Kako planirati transport da bi njegov trošak bio minimalan?

Hajde da problemu damo matematičku formulaciju. Označimo sa x 1 i x 2 količinu brašna koja se mora transportovati iz prvog skladišta u prvu i drugu fabriku, a sa x 3 i x 4 - iz drugog skladišta u prvu odnosno drugu fabriku. onda:

x 1 + x 2 = 50, x 3 + x 4 = 70, x 1 + x 3 = 40, x 2 + x 4 = 80. (1)

Ukupni trošak cjelokupnog transporta određuje se formulom

f = 1,2x 1 + 1,6x 2 + 0,8x 3 + x 4.

Sa matematičke tačke gledišta, problem je pronaći četiri broja x 1, x 2, x 3 i x 4 koji zadovoljavaju sve date uslove i daju minimum funkcije f. Rešimo sistem jednačina (1) za xi (i = 1, 2, 3, 4) eliminacijom nepoznanica. Shvatili smo to

x 1 = x 4 – 30, x 2 = 80 – x 4, x 3 = 70 – x 4, (2)

i x 4 se ne može odrediti jednoznačno. Kako je x i í 0 (i = 1, 2, 3, 4), iz jednačina (2) slijedi da je 30J x 4 J 70. Zamjenom izraza za x 1, x 2, x 3 u formulu za f dobijamo

f = 148 – 0,2x 4.

Lako je vidjeti da se minimum ove funkcije postiže pri maksimalnoj mogućoj vrijednosti x 4, odnosno pri x 4 = 70. Odgovarajuće vrijednosti ostalih nepoznanica određene su formulama (2): x 1 = 40, x 2 = 10, x 3 = 0.

4) Problem radioaktivnog raspada.

Neka je N(0) početni broj atoma radioaktivne supstance, a N(t) broj neraspadnutih atoma u trenutku t. Eksperimentalno je utvrđeno da je brzina promjene broja ovih atoma N"(t) proporcionalna N(t), odnosno N"(t)=–l N(t), l >0 je konstanta radioaktivnosti date supstance. U školskom kursu matematičke analize pokazano je da rješenje ove diferencijalne jednadžbe ima oblik N(t) = N(0)e –l t. Vrijeme T tokom kojeg se broj početnih atoma prepolovio naziva se poluživotom i važna je karakteristika radioaktivnosti tvari. Da bismo odredili T, moramo unijeti formulu Onda Na primjer, za radon l = 2,084 · 10 –6, pa prema tome T = 3,15 dana.

5) Problem trgovačkog putnika.

Prodavac koji živi u gradu A 1 treba da posjeti gradove A 2 , A 3 i A 4 , svaki grad tačno jednom, a zatim se vrati nazad u A 1 . Poznato je da su svi gradovi povezani u parove putevima, a dužine puteva b ij između gradova A i i A j (i, j = 1, 2, 3, 4) su sljedeće:

b 12 = 30, b 14 = 20, b 23 = 50, b 24 = 40, b 13 = 70, b 34 = 60.

Potrebno je odrediti redoslijed obilaska gradova u kojima je dužina odgovarajućeg puta minimalna.

Opišimo svaki grad kao tačku na ravni i označimo ga odgovarajućom oznakom Ai (i = 1, 2, 3, 4). Povežimo ove tačke pravim linijama: one će predstavljati puteve između gradova. Za svaki „put“ označavamo njegovu dužinu u kilometrima (slika 2). Rezultat je graf - matematički objekat koji se sastoji od određenog skupa tačaka na ravni (koji se nazivaju vrhovi) i određenog skupa linija koje povezuju ove tačke (zvane ivice). Štaviše, ovaj graf je označen, budući da su njegovim vrhovima i ivicama dodeljene neke oznake - brojevi (idovi) ili simboli (vertices). Ciklus na grafu je niz vrhova V 1 , V 2 , ..., V k , V 1 tako da su vrhovi V 1 , ..., V k različiti, a bilo koji par vrhova V i , V i+1 (i = 1, ..., k – 1) i par V 1, V k povezani su ivicom. Dakle, problem koji se razmatra je pronaći ciklus na grafu koji prolazi kroz sva četiri vrha za koji je zbir svih težina ivica minimalan. Hajde da pretražimo sve različite cikluse koji prolaze kroz četiri vrha i počinju od A 1:

1) A 1, A 4, A 3, A 2, A 1;
2) A 1, A 3, A 2, A 4, A 1;
3) A 1, A 3, A 4, A 2, A 1.

Nađimo sada dužine ovih ciklusa (u km): L 1 = 160, L 2 = 180, L 3 = 200. Dakle, ruta najkraće dužine je prva.

Imajte na umu da ako postoji n vrhova u grafu i svi vrhovi su povezani u parovima ivicama (takav graf se naziva kompletnim), tada je broj ciklusa koji prolaze kroz sve vrhove Dakle, u našem slučaju postoje tačno tri ciklusa.

6) Problem nalaženja veze između strukture i svojstava supstanci.

Pogledajmo nekoliko hemijskih jedinjenja zvanih normalni alkani. Sastoje se od n atoma ugljika i n + 2 atoma vodika (n = 1, 2 ...), međusobno povezanih kao što je prikazano na slici 3 za n = 3. Neka su poznate eksperimentalne vrijednosti tačaka ključanja ovih jedinjenja:

y e (3) = – 42°, y e (4) = 0°, y e (5) = 28°, y e (6) = 69°.

Potrebno je pronaći približan odnos između tačke ključanja i broja n za ova jedinjenja. Pretpostavimo da ova zavisnost ima oblik

y" a n+b,

Gdje a, b - konstante koje treba odrediti. Naći a i b u ovu formulu zamjenjujemo redom n = 3, 4, 5, 6 i odgovarajuće vrijednosti tačaka ključanja. Imamo:

– 42 » 3 a+ b, 0 » 4 a+ b, 28 » 5 a+ b, 69 » 6 a+ b.

Da odredimo najbolje a i b postoji mnogo različitih metoda. Koristimo najjednostavniji od njih. Izrazimo b kroz a iz ovih jednačina:

b » – 42 – 3 a, b " – 4 a, b » 28 – 5 a, b » 69 – 6 a.

Uzmimo aritmetičku sredinu ovih vrijednosti kao željeni b, odnosno stavimo b » 16 – 4,5 a. Zamenimo ovu vrednost b u originalni sistem jednačina i, računajući a, dobijamo za a sljedeće vrijednosti: a» 37, a» 28, a» 28, a" 36. Uzmimo kao potrebno a prosječnu vrijednost ovih brojeva, tj. stavimo a" 34. Dakle, tražena jednačina ima oblik

y » 34n – 139.

Provjerimo tačnost modela na originalna četiri spoja, za koje izračunavamo tačke ključanja koristeći rezultirajuću formulu:

y r (3) = – 37°, y r (4) = – 3°, y r (5) = 31°, y r (6) = 65°.

Dakle, greška u izračunavanju ove osobine za ova jedinjenja ne prelazi 5°. Dobivenu jednačinu koristimo za izračunavanje tačke ključanja jedinjenja sa n = 7, koje nije uključeno u originalni skup, za koji u ovu jednačinu zamenjujemo n = 7: y r (7) = 99°. Rezultat je bio prilično tačan: poznato je da je eksperimentalna vrijednost tačke ključanja y e (7) = 98°.

7) Problem određivanja pouzdanosti električnog kola.

Ovdje ćemo pogledati primjer probabilističkog modela. Prvo, predstavljamo neke informacije iz teorije vjerovatnoće - matematičke discipline koja proučava obrasce slučajnih pojava uočenih tokom ponovljenih ponavljanja eksperimenata. Nazovimo slučajni događaj A mogućim ishodom nekog eksperimenta. Događaji A 1, ..., A k čine kompletnu grupu ako se jedan od njih nužno javlja kao rezultat eksperimenta. Događaji se nazivaju nekompatibilnim ako se ne mogu dogoditi istovremeno u jednom iskustvu. Neka se događaj A dogodi m puta tokom n-strukog ponavljanja eksperimenta. Učestalost događaja A je broj W = . Očigledno, vrijednost W se ne može precizno predvidjeti dok se ne izvede serija od n eksperimenata. Međutim, priroda slučajnih događaja je takva da se u praksi ponekad uočava sljedeći efekat: kako se broj eksperimenata povećava, vrijednost praktično prestaje biti slučajna i stabilizuje se oko nekog neslučajnog broja P(A), koji se naziva vjerovatnoća događaj A. Za nemoguć događaj (koji se nikada ne dešava u eksperimentu) P(A)=0, a za pouzdan događaj (koji se uvek dešava u iskustvu) P(A)=1. Ako događaji A 1 , ..., A k čine kompletnu grupu nekompatibilnih događaja, tada je P(A 1)+...+P(A k)=1.

Neka se, na primjer, eksperiment sastoji od bacanja kocke i posmatranja broja izbačenih tačaka X. Tada možemo uvesti sljedeće slučajne događaje A i = (X = i), i = 1, ..., 6. Oni čine kompletnu grupu nekompatibilnih jednako verovatnih događaja, stoga P(A i) = (i = 1, ..., 6).

Zbir događaja A i B je događaj A + B, koji se sastoji u činjenici da se barem jedan od njih javlja u iskustvu. Proizvod događaja A i B je događaj AB, koji se sastoji od istovremene pojave ovih događaja. Za nezavisne događaje A i B, istinite su sljedeće formule:

P(AB) = P(A) P(B), P(A + B) = P(A) + P(B).

8) Razmotrimo sada sljedeće zadatak. Pretpostavimo da su tri elementa povezana u seriju u električni krug i rade nezavisno jedan od drugog. Vjerovatnoće kvara 1., 2. i 3. elementa su redom jednake P1 = 0,1, P2 = 0,15, P3 = 0,2. Kolo ćemo smatrati pouzdanim ako je vjerovatnoća da neće biti struje u kolu nije veća od 0,4. Potrebno je utvrditi da li je dato kolo pouzdano.

Budući da su elementi povezani u seriju, neće biti struje u kolu (događaj A) ako barem jedan od elemenata pokvari. Neka je A i događaj da i-ti element radi (i = 1, 2, 3). Tada je P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Očigledno, A 1 A 2 A 3 je događaj u kojem sva tri elementa rade istovremeno, i

P(A 1 A 2 A 3) = P(A 1) P(A 2) P(A 3) = 0,612.

Tada je P(A) + P(A 1 A 2 A 3) = 1, pa je P(A) = 0,388< 0,4. Следовательно, цепь является надежной.

U zaključku, napominjemo da su dati primjeri matematičkih modela (uključujući funkcionalne i strukturne, determinističke i probabilističke) ilustrativne prirode i, očigledno, ne iscrpljuju raznolikost matematičkih modela koji se javljaju u prirodnim i humanističkim naukama.

U ovom članku nudimo primjere matematičkih modela. Pored toga, obratićemo pažnju na faze kreiranja modela i analizirati neke probleme vezane za matematičko modeliranje.

Drugo pitanje koje imamo jesu matematički modeli u ekonomiji, čije ćemo primjere definiciju pogledati malo kasnije. Predlažemo da započnemo naš razgovor sa samim konceptom „modela“, ukratko razmotrimo njihovu klasifikaciju i pređemo na naša glavna pitanja.

Koncept "modela"

Često čujemo riječ “model”. Šta je? Ovaj pojam ima mnogo definicija, evo samo tri od njih:

specifičan objekat koji je kreiran za primanje i pohranjivanje informacija, koje odražavaju neka svojstva ili karakteristike, itd., originala ovog objekta (ovaj specifični objekt može se izraziti u različitim oblicima: mentalni, opis pomoću znakova i tako dalje);
Model takođe znači predstavljanje specifične situacije, života ili upravljanja;
model može biti umanjena kopija objekta (kreirani su za detaljnije proučavanje i analizu, budući da model odražava strukturu i odnose).

Na osnovu svega što je ranije rečeno, možemo izvući mali zaključak: model vam omogućava da detaljno proučavate složeni sistem ili objekt.

Svi modeli se mogu klasifikovati prema nizu karakteristika:

po oblasti upotrebe (obrazovne, eksperimentalne, naučno-tehničke, igre, simulacije);
po dinamici (statička i dinamička);
po grani znanja (fizička, hemijska, geografska, istorijska, sociološka, ekonomska, matematička);
po načinu prezentacije (materijalno i informativno).

Informacijski modeli se, pak, dijele na simboličke i verbalne. I simbolične - na kompjuterske i neračunarske. Pređimo sada na detaljno razmatranje primjera matematičkog modela.

Matematički model

Kao što možete pretpostaviti, matematički model odražava sve karakteristike objekta ili fenomena koristeći posebne matematičke simbole. Matematika je potrebna da bi modelirala obrasce okolnog svijeta na svom specifičnom jeziku.

Metoda matematičkog modeliranja nastala je prilično davno, prije više hiljada godina, zajedno sa pojavom ove nauke. Međutim, podsticaj razvoju ove metode modeliranja dala je pojava računara (elektronskih računara).

Pređimo sada na klasifikaciju. Može se izvesti i prema nekim znakovima. Oni su predstavljeni u donjoj tabeli.

Predlažemo da se zaustavimo i pobliže pogledamo najnoviju klasifikaciju, jer ona odražava opće obrasce modeliranja i ciljeve modela koji se kreiraju.

Deskriptivni modeli

U ovom poglavlju predlažemo da se detaljnije zadržimo na deskriptivnim matematičkim modelima. Da bi sve bilo vrlo jasno, dat će se primjer.

Počnimo s činjenicom da se ovaj tip može nazvati deskriptivnim. To je zbog činjenice da jednostavno radimo kalkulacije i prognoze, ali ni na koji način ne možemo utjecati na ishod događaja.

Upečatljiv primjer deskriptivnog matematičkog modela je proračun putanje leta, brzine i udaljenosti od Zemlje komete koja je napala prostranstva našeg Sunčevog sistema. Ovaj model je deskriptivan, jer nas svi dobijeni rezultati mogu samo upozoriti na bilo kakvu opasnost. Nažalost, ne možemo uticati na ishod događaja. Međutim, na osnovu dobijenih proračuna moguće je poduzeti bilo kakve mjere za očuvanje života na Zemlji.

Optimizacijski modeli

Sada ćemo malo govoriti o ekonomskim i matematičkim modelima, čiji primjeri mogu poslužiti kao različite trenutne situacije. U ovom slučaju govorimo o modelima koji pomažu u pronalaženju tačnog odgovora pod određenim uvjetima. Definitivno imaju neke parametre. Da bude potpuno jasno, pogledajmo primjer iz poljoprivrednog sektora.

Imamo žitnicu, ali se žito vrlo brzo pokvari. U tom slučaju moramo odabrati prave temperaturne uvjete i optimizirati proces skladištenja.

Dakle, možemo definisati koncept „modela optimizacije“. U matematičkom smislu, to je sistem jednačina (linearnih i ne), čije rješenje pomaže u pronalaženju optimalnog rješenja u konkretnoj ekonomskoj situaciji. Pogledali smo primjer matematičkog modela (optimizacija), ali želim da dodam: ovaj tip spada u klasu ekstremnih problema, oni pomažu u opisu funkcionisanja ekonomskog sistema.

Napominjemo još jednu nijansu: modeli mogu biti različite prirode (vidi tabelu u nastavku).

Višekriterijumski modeli

Sada vas pozivamo da malo popričamo o matematičkom modelu višekriterijumske optimizacije. Prije ovoga dali smo primjer matematičkog modela za optimizaciju procesa prema bilo kojem kriteriju, ali što ako ih ima mnogo?

Upečatljiv primjer višekriterijumskog zadatka je organizacija pravilne, zdrave i istovremeno ekonomične ishrane za velike grupe ljudi. Ovakvi zadaci se često susreću u vojsci, školskim menzama, letnjim kampovima, bolnicama i tako dalje.

Koji su nam kriterijumi dati u ovom zadatku?

Ishrana treba da bude zdrava.
Troškovi hrane trebaju biti minimalni.

Kao što vidite, ovi ciljevi se uopšte ne poklapaju. To znači da je prilikom rješavanja problema potrebno tražiti optimalno rješenje, balans između dva kriterija.

Modeli igara

Kada govorimo o modelima igara, potrebno je razumjeti pojam „teorije igara“. Jednostavno rečeno, ovi modeli odražavaju matematičke modele stvarnih sukoba. Samo morate shvatiti da, za razliku od pravog sukoba, matematički model igre ima svoja specifična pravila.

Sada ćemo dati minimum informacija iz teorije igara koje će vam pomoći da shvatite šta je model igre. Dakle, model nužno sadrži stranke (dvije ili više), koje se obično nazivaju igračima.

Svi modeli imaju određene karakteristike.

Model igre može biti uparen ili višestruki. Ako imamo dva subjekta, onda je sukob uparen; ako ih ima više, on je višestruk. Također možete razlikovati antagonističku igru, također se zove igra sa nultom sumom. Ovo je model u kojem je dobitak jednog od učesnika jednak gubitku drugog.

Simulacijski modeli

U ovom odeljku obratićemo pažnju na simulacione matematičke modele. Primjeri zadataka uključuju:

model dinamike populacije mikroorganizama;
model molekularnog kretanja i tako dalje.

U ovom slučaju govorimo o modelima koji su što bliže stvarnim procesima. Uglavnom, imitiraju neku manifestaciju u prirodi. U prvom slučaju, na primjer, možemo simulirati dinamiku broja mrava u jednoj koloniji. Istovremeno, možete posmatrati sudbinu svakog pojedinca. U ovom slučaju se rijetko koristi matematički opis, češće su prisutni pisani uvjeti:

nakon pet dana ženka polaže jaja;
nakon dvadeset dana mrav umire i tako dalje.

Stoga se koriste za opisivanje velikog sistema. Matematički zaključak je obrada dobijenih statističkih podataka.

Zahtjevi

Vrlo je važno znati da ovaj tip modela ima neke zahtjeve, uključujući i one navedene u donjoj tabeli.

Svestranost	Ovo svojstvo vam omogućava da koristite isti model kada opisujete slične grupe objekata. Važno je napomenuti da su univerzalni matematički modeli potpuno nezavisni od fizičke prirode objekta koji se proučava.
Adekvatnost	Ovdje je važno shvatiti da vam ovo svojstvo omogućava da što preciznije reprodukujete stvarne procese. U operativnim zadacima ovo svojstvo matematičkog modeliranja je veoma važno. Primjer modela je proces optimizacije korištenja plinskog sistema. U ovom slučaju se upoređuju izračunati i stvarni pokazatelji, kao rezultat toga, provjerava se ispravnost sastavljenog modela
Preciznost	Ovaj zahtjev podrazumijeva podudarnost vrijednosti koje dobijemo prilikom izračunavanja matematičkog modela i ulaznih parametara našeg stvarnog objekta
Ekonomičan	Zahtjev isplativosti za bilo koji matematički model karakteriziraju troškovi implementacije. Ako s modelom radite ručno, tada morate izračunati koliko će vremena biti potrebno za rješavanje jednog problema pomoću ovog matematičkog modela. Ako govorimo o kompjuterski potpomognutom dizajnu, onda se izračunavaju pokazatelji vremena i troškova memorije računala

Faze modeliranja

Ukupno, matematičko modeliranje se obično dijeli u četiri faze.

Formulacija zakona koji povezuju dijelove modela.
Proučavanje matematičkih problema.
Utvrđivanje podudarnosti praktičnih i teorijskih rezultata.
Analiza i modernizacija modela.

Ekonomsko-matematički model

U ovom dijelu ćemo ukratko istaknuti problem. Primjeri zadataka uključuju:

formiranje proizvodnog programa za proizvodnju mesnih prerađevina koji osigurava maksimalan proizvodni profit;
maksimiziranje profita organizacije izračunavanjem optimalne količine stolova i stolica proizvedenih u fabrici namještaja, itd.

Ekonomsko-matematički model prikazuje ekonomsku apstrakciju koja se izražava matematičkim terminima i simbolima.

Računarski matematički model

Primjeri kompjuterskog matematičkog modela su:

hidraulički problemi pomoću dijagrama toka, dijagrama, tabela, itd.;
problemi na mehanici čvrstog materijala, i tako dalje.

Kompjuterski model je slika objekta ili sistema, predstavljena u obliku:

stolovi;
blok dijagrami;
dijagrami;
grafike i tako dalje.

Štaviše, ovaj model odražava strukturu i međusobne veze sistema.

Izgradnja ekonomsko-matematičkog modela

Već smo govorili o tome šta je ekonomsko-matematički model. Sada ćemo razmotriti primjer rješavanja problema. Moramo analizirati proizvodni program kako bismo identifikovali rezervu za povećanje profita sa pomakom u asortimanu.

Nećemo u potpunosti razmatrati problem, već ćemo samo izgraditi ekonomski i matematički model. Kriterijum našeg zadatka je maksimizacija profita. Tada funkcija ima oblik: A=r1*h1+r2*h2..., teži maksimumu. U ovom modelu, p je profit po jedinici, a x je broj proizvedenih jedinica. Zatim, na osnovu konstruisanog modela, potrebno je izvršiti proračune i sumirati.

Primjer izgradnje jednostavnog matematičkog modela

Zadatak. Ribar se vratio sa sljedećim ulovom:

8 riba - stanovnici sjevernih mora;
20% ulova su stanovnici južnih mora;
Iz lokalne rijeke nije pronađena nijedna riba.

Koliko je ribe kupio u radnji?

Dakle, primjer konstruiranja matematičkog modela ovog problema izgleda ovako. Ukupan broj riba označavamo sa x. Slijedeći uvjet, 0,2x je broj riba koje žive u južnim geografskim širinama. Sada kombinujemo sve dostupne informacije i dobijamo matematički model problema: x=0,2x+8. Rješavamo jednačinu i dobivamo odgovor na glavno pitanje: kupio je 10 riba u trgovini.

Predavanje 1.

METODOLOŠKE OSNOVE MODELIRANJA

Trenutno stanje problema modeliranja sistema

Koncepti modeliranja i simulacije

Modeliranje može se smatrati zamjenom predmeta proučavanja (originala) njegovom konvencionalnom slikom, opisom ili drugim objektom tzv. model i pružanje ponašanja bliskog originalu u okviru određenih pretpostavki i prihvatljivih grešaka. Modeliranje se obično izvodi s ciljem razumijevanja svojstava originala proučavanjem njegovog modela, a ne samog objekta. Naravno, modeliranje je opravdano kada je jednostavnije od stvaranja samog originala, ili kada je iz nekog razloga bolje uopće ne stvarati original.

Ispod model Pod pojmom se podrazumijeva fizički ili apstraktni objekt čija su svojstva u određenom smislu slična svojstvima predmeta koji se proučava.U ovom slučaju zahtjevi za modelom su određeni problemom koji se rješava i raspoloživim sredstvima. Postoji nekoliko općih zahtjeva za modele:

2) potpunost – pružanje svih potrebnih informacija primaocu

o objektu;

3) fleksibilnost – sposobnost reprodukcije različitih situacija u svemu

raspon promjena uslova i parametara;

4) složenost razvoja mora biti prihvatljiva za postojeće

vremena i softvera.

Modeliranje je proces konstruisanja modela objekta i proučavanja njegovih svojstava ispitivanjem modela.

Dakle, modeliranje uključuje 2 glavne faze:

1) razvoj modela;

2) proučavanje modela i izvođenje zaključaka.

Istovremeno se u svakoj fazi rješavaju različiti zadaci i

suštinski različite metode i sredstva.

U praksi se koriste različite metode modeliranja. Ovisno o načinu implementacije, svi modeli se mogu podijeliti u dvije velike klase: fizičke i matematičke.

Matematičko modeliranje Obično se smatra sredstvom za proučavanje procesa ili pojava koristeći njihove matematičke modele.

Ispod fizičko modeliranje odnosi se na proučavanje objekata i pojava na fizičkim modelima, kada se proces koji se proučava reproducira uz očuvanje njegove fizičke prirode ili se koristi drugi fizički fenomen sličan onom koji se proučava. Gde fizički modeli Oni po pravilu pretpostavljaju stvarno oličenje onih fizičkih svojstava originala koja su značajna u određenoj situaciji.Na primjer, prilikom projektovanja novog aviona, kreira se maketa koja ima ista aerodinamička svojstva; Prilikom planiranja razvoja, arhitekti izrađuju model koji odražava prostorni raspored njegovih elemenata. U tom smislu se naziva i fizičko modeliranje izrada prototipa.

Modeliranje poluživota je studija upravljivih sistema na modeliranju kompleksa uz uključivanje stvarne opreme u model. Zatvoreni model, pored realne opreme, uključuje simulatore uticaja i smetnji, matematičke modele spoljašnjeg okruženja i procesa za koje nije poznat dovoljno tačan matematički opis. Uključivanje stvarne opreme ili realnih sistema u krug modeliranja složenih procesa omogućava smanjenje apriorne nesigurnosti i istraživanje procesa za koje ne postoji tačan matematički opis. Koristeći poluprirodno modeliranje, istraživanje se provodi uzimajući u obzir male vremenske konstante i linearnosti svojstvene stvarnoj opremi. Prilikom proučavanja modela koristeći stvarnu opremu, koristi se koncept dinamička simulacija, prilikom proučavanja složenih sistema i pojava - evolucijski, imitacija I kibernetičko modeliranje.

Očigledno, stvarna korist od modeliranja može se postići samo ako su ispunjena dva uslova:

1) model daje ispravan (adekvatan) prikaz svojstava

original, značajan sa stanovišta operacije koja se proučava;

2) model vam omogućava da eliminišete probleme navedene iznad inherentne

vršenje istraživanja na stvarnim objektima.

2. Osnovni koncepti matematičkog modeliranja

Rješavanje praktičnih zadataka matematičkim metodama dosljedno se provodi formulisanjem problema (razvijanjem matematičkog modela), odabirom metode za proučavanje rezultirajućeg matematičkog modela i analizom dobivenog matematičkog rezultata. Matematička formulacija problema obično se predstavlja u obliku geometrijskih slika, funkcija, sistema jednačina itd. Opis objekta (fenomena) može se predstaviti pomoću kontinuiranih ili diskretnih, determinističkih ili stohastičkih i drugih matematičkih oblika.

Teorija matematičkog modeliranja osigurava identifikaciju obrazaca pojavljivanja različitih pojava u okolnom svijetu ili rada sistema i uređaja putem njihovog matematičkog opisa i modeliranja bez izvođenja testova u punoj mjeri. U ovom slučaju se koriste odredbe i zakoni matematike koji opisuju simulirane pojave, sisteme ili uređaje na nekom nivou njihove idealizacije.

matematički model (MM) je formalizirani opis sistema (ili operacije) u nekom apstraktnom jeziku, na primjer, u obliku skupa matematičkih odnosa ili dijagrama algoritma, tj. tj. takav matematički opis koji omogućava simulaciju rada sistema ili uređaja na nivou koji je dovoljno blizak njihovom stvarnom ponašanju dobijenom tokom testiranja sistema ili uređaja u punoj mjeri.

Svaki MM opisuje stvarni predmet, pojavu ili proces sa određenim stepenom aproksimacije stvarnosti. Tip MM zavisi kako od prirode stvarnog objekta tako i od ciljeva studije.

Matematičko modeliranje društvenih, ekonomskih, bioloških i fizičkih pojava, objekata, sistema i raznih uređaja jedno je od najvažnijih sredstava razumijevanja prirode i dizajniranja širokog spektra sistema i uređaja. Poznati su primjeri efikasne upotrebe modeliranja u stvaranju nuklearnih tehnologija, zrakoplovnih i svemirskih sistema, u predviđanju atmosferskih i okeanskih pojava, vremena itd.

Međutim, tako ozbiljne oblasti modeliranja često zahtijevaju superkompjutere i godine rada velikih timova naučnika na pripremi podataka za modeliranje i njihovo otklanjanje grešaka. Međutim, u ovom slučaju, matematičko modeliranje složenih sistema i uređaja ne samo da štedi novac na istraživanju i testiranju, već može i eliminirati ekološke katastrofe - na primjer, omogućava vam da odustanete od testiranja nuklearnog i termonuklearnog oružja u korist njihovog matematičkog modeliranja. ili testiranje vazduhoplovnih sistema pre njihovih stvarnih letova.Između Stoga je matematičko modeliranje na nivou rešavanja jednostavnijih problema, na primer, iz oblasti mehanike, elektrotehnike, elektronike, radiotehnike i mnogih drugih oblasti nauke i tehnologije sada postalo dostupan za izvođenje na modernim računarima. A kada se koriste generalizirani modeli, postaje moguće simulirati prilično složene sisteme, na primjer, telekomunikacijske sustave i mreže, radarske ili radio-navigacijske sustave.

Svrha matematičkog modeliranja je analiza stvarnih procesa (u prirodi ili tehnologiji) korištenjem matematičkih metoda. Zauzvrat, ovo zahtijeva formalizaciju MM procesa koji treba proučavati.Model može biti matematički izraz koji sadrži varijable čije je ponašanje slično ponašanju realnog sistema.Model može uključivati elemente slučajnosti koji uzimaju u obzir vjerovatnoće moguće akcije dva ili više „igrača“, kao, na primjer, u teorijskim igrama; ili može predstavljati stvarne varijable međusobno povezanih dijelova operativnog sistema.

Matematičko modeliranje za proučavanje karakteristika sistema može se podeliti na analitičko, simulaciono i kombinovano. Zauzvrat, MM se dijele na simulacijske i analitičke.

Analitičko modeliranje

Za analitičko modeliranje Karakteristično je da su procesi funkcionisanja sistema zapisani u obliku određenih funkcionalnih odnosa (algebarske, diferencijalne, integralne jednačine). Analitički model se može proučavati korištenjem sljedećih metoda:

1) analitičke, kada nastoje da dobiju, u opštem obliku, eksplicitne zavisnosti za karakteristike sistema;

2) numeričke, kada nije moguće naći rešenje jednačina u opštem obliku i one se rešavaju za određene početne podatke;

3) kvalitativni, kada se u odsustvu rješenja pronađu neka njegova svojstva.

Analitički modeli se mogu dobiti samo za relativno jednostavne sisteme. Za složene sisteme često se javljaju veliki matematički problemi. Za primjenu analitičke metode ide se na značajno pojednostavljenje originalnog modela. Međutim, istraživanje korištenjem pojednostavljenog modela pomaže da se dobiju samo indikativni rezultati. Analitički modeli matematički ispravno odražavaju odnos između ulaznih i izlaznih varijabli i parametara. Ali njihova struktura ne odražava unutrašnju strukturu objekta.

Tokom analitičkog modeliranja njegovi rezultati se prikazuju u obliku analitičkih izraza. Na primjer, povezivanjem R.C.- spoj na izvor konstantnog napona E(R, C I E- komponente ovog modela), možemo napraviti analitički izraz za vremensku zavisnost napona u(t) na kondenzatoru C:

Ova linearna diferencijalna jednadžba (DE) je analitički model ovog jednostavnog linearnog kola. Njegovo analitičko rješenje, pod početnim uslovom u(0) = 0, što znači ispražnjeni kondenzator C na početku modeliranja, omogućava vam da pronađete željenu ovisnost - u obliku formule:

u(t) = E(1− exstr(- t/RC)). (2)

Međutim, čak iu ovom najjednostavnijem primjeru, potrebni su određeni napori da se riješi DE (1) ili da se primijeni kompjuterski matematički sistemi(SCM) sa simboličkim proračunima – sistemi kompjuterske algebre. Za ovaj potpuno trivijalan slučaj, rješavanje problema modeliranja linearne R.C.-kolo daje analitički izraz (2) prilično općenitog oblika - pogodno je za opisivanje rada kola za bilo koju vrijednost komponenti R, C I E, i opisuje eksponencijalni naboj kondenzatora C kroz otpornik R iz izvora konstantnog napona E.

Naravno, pronalaženje analitičkih rješenja tokom analitičkog modeliranja pokazuje se izuzetno vrijednim za identifikaciju općih teorijskih obrazaca jednostavnih linearnih kola, sistema i uređaja, međutim, njegova složenost naglo raste kako utjecaji na model postaju složeniji, a redoslijed i broj jednadžbe stanja koje opisuju povećanje modeliranog objekta. Možete dobiti manje ili više vidljive rezultate kada modelirate objekte drugog ili trećeg reda, ali s višim redom, analitički izrazi postaju preglomazni, složeni i teško razumljivi. Na primjer, čak i jednostavno elektronsko pojačalo često sadrži desetke komponenti. Međutim, mnogi moderni SCM-ovi, na primjer, sistemi simboličke matematike Maple, Mathematica ili okolina MATLAB, sposobni su u velikoj mjeri automatizirati rješavanje složenih problema analitičkog modeliranja.

Jedna vrsta modeliranja je numeričko modeliranje, koji se sastoji u dobijanju potrebnih kvantitativnih podataka o ponašanju sistema ili uređaja bilo kojom odgovarajućom numeričkom metodom, kao što su Euler ili Runge-Kutta metode. U praksi se pokazalo da je modeliranje nelinearnih sistema i uređaja pomoću numeričkih metoda mnogo efikasnije od analitičkog modeliranja pojedinačnih privatnih linearnih kola, sistema ili uređaja. Na primjer, za rješavanje DE (1) ili DE sistema u složenijim slučajevima ne može se dobiti rješenje u analitičkom obliku, ali pomoću podataka numeričke simulacije možete dobiti prilično potpune podatke o ponašanju simuliranih sistema i uređaja, kao i kao konstruisati grafove zavisnosti koji opisuju ovo ponašanje.

Simulacijsko modeliranje

At imitacija 10 i modeliranje, algoritam koji implementira model reproducira proces funkcionisanja sistema tokom vremena. Simuliraju se elementarne pojave koje čine proces, čuvajući njihovu logičku strukturu i slijed događaja tokom vremena.

Glavna prednost simulacijskih modela u odnosu na analitičke je sposobnost rješavanja složenijih problema.

Simulacijski modeli olakšavaju uzimanje u obzir prisutnosti diskretnih ili kontinuiranih elemenata, nelinearnih karakteristika, slučajnih utjecaja, itd. Stoga se ova metoda široko koristi u fazi projektovanja složenih sistema. Glavno sredstvo implementacije simulacionog modeliranja je kompjuter, koji omogućava digitalno modeliranje sistema i signala.

S tim u vezi, definišimo izraz „ kompjutersko modeliranje“, koji se sve više koristi u literaturi. Pretpostavimo to kompjutersko modeliranje je matematičko modeliranje pomoću računarske tehnologije. U skladu s tim, tehnologija kompjuterskog modeliranja uključuje izvođenje sljedećih radnji:

1) određivanje svrhe modeliranja;

2) razvoj konceptualnog modela;

3) formalizacija modela;

4) softverska implementacija modela;

5) planiranje eksperimenata modela;

6) sprovođenje eksperimentalnog plana;

7) analiza i interpretacija rezultata modeliranja.

At simulacijsko modeliranje korišteni MM reproducira algoritam („logiku“) funkcionisanja sistema koji se proučava tokom vremena za različite kombinacije vrijednosti parametara sistema i vanjskog okruženja.

Primjer najjednostavnijeg analitičkog modela je jednadžba pravolinijskog ravnomjernog kretanja. Prilikom proučavanja ovakvog procesa korištenjem simulacijskog modela, potrebno je implementirati promatranje promjena u pređenoj putanji tokom vremena.Očigledno je da je u nekim slučajevima poželjnije analitičko modeliranje, u drugim - simulacija (ili kombinacija oba). Da biste napravili uspješan izbor, morate odgovoriti na dva pitanja.

Koja je svrha modeliranja?

U koju se klasu može klasificirati modelirani fenomen?

Odgovori na oba ova pitanja mogu se dobiti tokom prve dvije faze modeliranja.

Simulacijski modeli ne samo po svojstvima, već i po strukturi odgovaraju modeliranom objektu. U ovom slučaju postoji nedvosmislena i očigledna korespondencija između procesa dobijenih na modelu i procesa koji se dešavaju na objektu. Nedostatak simulacije je što je potrebno mnogo vremena da se riješi problem kako bi se postigla dobra tačnost.

Rezultati simulacionog modeliranja rada stohastičkog sistema su realizacije slučajnih varijabli ili procesa. Stoga su za pronalaženje karakteristika sistema potrebna višestruka ponavljanja i naknadna obrada podataka. Najčešće se u ovom slučaju koristi vrsta simulacije - statistički

modeliranje(ili Monte Carlo metoda), tj. reprodukcija slučajnih faktora, događaja, veličina, procesa, polja u modelima.

Na osnovu rezultata statističkog modeliranja određuju se procjene vjerovatnostnih kriterijuma kvaliteta, opštih i specifičnih, koji karakterišu funkcionisanje i efikasnost upravljanog sistema. Statističko modeliranje se široko koristi za rješavanje naučnih i primijenjenih problema u različitim oblastima nauke i tehnologije. Metode statističkog modeliranja se široko koriste u proučavanju složenih dinamičkih sistema, ocjenjivanju njihovog funkcionisanja i efikasnosti.

Završna faza statističkog modeliranja zasniva se na matematičkoj obradi dobijenih rezultata. Ovdje se koriste metode matematičke statistike (parametrijska i neparametarska procjena, testiranje hipoteza). Primjer parametarskog estimatora je srednja vrijednost uzorka mjere učinka. Među neparametarskim metodama, široko rasprostranjena histogramska metoda.

Razmatrana shema je zasnovana na ponovljenim statističkim ispitivanjima sistema i metoda statistike nezavisnih slučajnih varijabli, koja nije uvijek prirodna u praksi i optimalna u smislu troškova. Smanjenje vremena testiranja sistema može se postići upotrebom preciznijih metoda evaluacije. Kao što je poznato iz matematičke statistike, efektivne procjene imaju najveću tačnost za datu veličinu uzorka. Optimalno filtriranje i metoda maksimalne vjerovatnoće daju opći metod za dobivanje takvih procjena.U problemima statističkog modeliranja, obrada implementacija slučajnih procesa je neophodna ne samo za analizu izlaznih procesa.

Kontrola karakteristika ulaznih slučajnih uticaja je takođe veoma važna. Kontrola se sastoji od provjere usklađenosti distribucija generiranih procesa sa datim distribucijama. Ovaj problem se često formuliše kao problem testiranja hipoteza.

Opšti trend u kompjuterskom modeliranju složenih kontrolisanih sistema je želja da se skrati vreme modeliranja, kao i da se istraživanja sprovedu u realnom vremenu. Pogodno je predstaviti računske algoritme u ponavljajućem obliku, omogućavajući njihovu implementaciju brzinom prijema trenutnih informacija.

PRINCIPI SISTEMSKOG PRISTUPA U MODELIRANJU

Osnovni principi teorije sistema

Osnovni principi teorije sistema nastali su tokom proučavanja dinamičkih sistema i njihovih funkcionalnih elemenata. Sistem se shvata kao grupa međusobno povezanih elemenata koji deluju zajedno da bi postigli unapred određeni zadatak. Analiza sistema nam omogućava da odredimo najrealnije načine za obavljanje datog zadatka, obezbeđujući maksimalno zadovoljenje navedenih zahteva.

Elementi koji čine osnovu teorije sistema ne stvaraju se hipotezama, već se otkrivaju eksperimentalno. Da bi se pristupilo izgradnji sistema, potrebno je imati opšte karakteristike tehnoloških procesa. Isto važi i za principe kreiranja matematički formulisanih kriterijuma koje proces ili njegov teorijski opis mora da zadovolji. Modeliranje je jedna od najvažnijih metoda naučnog istraživanja i eksperimentiranja.

Prilikom konstruisanja modela objekata koristi se sistemski pristup, koji je metodologija za rešavanje složenih problema, koja se zasniva na posmatranju objekta kao sistema koji funkcioniše u određenom okruženju. Sistematski pristup podrazumeva otkrivanje integriteta objekta, identifikaciju i proučavanje njegove unutrašnje strukture, kao i veze sa spoljašnjim okruženjem. U ovom slučaju, objekt je predstavljen kao dio stvarnog svijeta koji je izoliran i proučavan u vezi s problemom konstruiranja modela. Osim toga, sistemski pristup uključuje konzistentan prijelaz od opšteg ka specifičnom, kada je cilj dizajna osnova razmatranja, a objekt se razmatra u odnosu na okolinu.

Složeni objekat se može podijeliti na podsisteme, koji su dijelovi objekta koji ispunjavaju sljedeće zahtjeve:

1) podsistem je funkcionalno nezavisan deo objekta. Povezan je sa drugim podsistemima, razmenjuje informacije i energiju sa njima;

2) za svaki podsistem mogu se definisati funkcije ili svojstva koja se ne poklapaju sa svojstvima celog sistema;

3) svaki od podsistema može biti podvrgnut daljoj podeli na nivo elemenata.

U ovom slučaju, element se shvata kao podsistem nižeg nivoa, čija je dalja podela neprikladna sa stanovišta problema koji se rešava.

Dakle, sistem se može definisati kao reprezentacija objekta u obliku skupa podsistema, elemenata i veza u cilju njegovog stvaranja, istraživanja ili poboljšanja. U ovom slučaju, prošireni prikaz sistema, uključujući glavne podsisteme i veze između njih, naziva se makrostruktura, a detaljno otkrivanje unutrašnje strukture sistema do nivoa elemenata naziva se mikrostruktura.

Uz sistem obično postoji i supersistem - sistem višeg nivoa, koji uključuje predmetni objekat, a funkcija bilo kog sistema može se odrediti samo preko supersistema.

Neophodno je istaći pojam okruženja kao skupa objekata spoljašnjeg sveta koji značajno utiču na efikasnost sistema, ali nisu deo sistema i njegovog nadsistema.

U vezi sa sistemskim pristupom građenju modela koristi se koncept infrastrukture koji opisuje odnos sistema sa njegovom okolinom (okruženjem).U ovom slučaju se identifikuju, opisuju i proučavaju svojstva objekta koja su bitna. u okviru određenog zadatka naziva se stratifikacija objekta, a svaki model objekta je njegov stratifikovani opis.

Za sistemski pristup važno je odrediti strukturu sistema, tj. skup veza između elemenata sistema, koji odražava njihovu interakciju. Da bismo to učinili, prvo ćemo razmotriti strukturne i funkcionalne pristupe modeliranju.

Strukturalnim pristupom otkriva se sastav odabranih elemenata sistema i veze između njih. Skup elemenata i veza nam omogućava da prosudimo strukturu sistema. Najopštiji opis strukture je topološki opis. Omogućava vam da odredite komponente sistema i njihove veze pomoću grafova. Manje je uopšten funkcionalni opis, kada se razmatraju pojedinačne funkcije, tj. algoritmi za ponašanje sistema. U ovom slučaju se implementira funkcionalni pristup koji definira funkcije koje sistem obavlja.

Na osnovu sistemskog pristupa može se predložiti slijed razvoja modela, kada se razlikuju dvije glavne faze projektovanja: makrodizajn i mikrodizajn.

U fazi makro-dizajna izgrađuje se model eksternog okruženja, identifikuju resursi i ograničenja, odabiru sistemski model i kriterijume za procenu adekvatnosti.

Faza mikro dizajna u velikoj mjeri ovisi o specifičnoj vrsti odabranog modela. Općenito, uključuje kreiranje informacionih, matematičkih, tehničkih i softverskih sistema za modeliranje. U ovoj fazi utvrđuju se glavne tehničke karakteristike kreiranog modela, procjenjuju se vrijeme potrebno za rad s njim i trošak resursa za postizanje navedenog kvaliteta modela.

Bez obzira na vrstu modela, prilikom njegove izgradnje potrebno je voditi se nizom principa sistematskog pristupa:

1) dosledno napredovanje kroz faze kreiranja modela;

2) koordinaciju informacija, resursa, pouzdanosti i drugih karakteristika;

3) ispravan odnos između različitih nivoa konstrukcije modela;

4) integritet pojedinih faza projektovanja modela.

Za izradu matematičkog modela potrebno je:

pažljivo analizirati stvarni predmet ili proces;
istaći njegove najznačajnije karakteristike i svojstva;
definisati varijable, tj. parametri čije vrijednosti utječu na glavne karakteristike i svojstva objekta;
opisuju ovisnost osnovnih svojstava objekta, procesa ili sistema o vrijednostima varijabli koristeći logičko-matematičke odnose (jednačine, jednakosti, nejednačine, logičko-matematičke konstrukcije);
istaći unutrašnje veze objekta, procesa ili sistema koristeći ograničenja, jednačine, jednakosti, nejednakosti, logičke i matematičke konstrukcije;
identificirati vanjske veze i opisati ih koristeći ograničenja, jednačine, jednakosti, nejednakosti, logičke i matematičke konstrukcije.

Matematičko modeliranje, osim proučavanja objekta, procesa ili sistema i izrade njegovog matematičkog opisa, uključuje i:

izgradnju algoritma koji modelira ponašanje objekta, procesa ili sistema;
provjera adekvatnosti modela i objekta, procesa ili sistema na osnovu računskih i eksperimenata u punoj mjeri;
prilagođavanje modela;
koristeći model.

Matematički opis procesa i sistema koji se proučavaju zavisi od:

prirodu realnog procesa ili sistema i sastavlja se na osnovu zakona fizike, hemije, mehanike, termodinamike, hidrodinamike, elektrotehnike, teorije plastičnosti, teorije elastičnosti itd.
potrebnu pouzdanost i tačnost proučavanja i istraživanja realnih procesa i sistema.

Izgradnja matematičkog modela obično počinje izgradnjom i analizom najjednostavnijeg, najgrubljeg matematičkog modela predmeta, procesa ili sistema koji se razmatra. U budućnosti, ako je potrebno, model se dorađuje i njegova korespondencija sa objektom postaje potpunija.

Uzmimo jednostavan primjer. Potrebno je odrediti površinu radnog stola. Obično se to radi mjerenjem njegove dužine i širine, a zatim množenjem rezultirajućih brojeva. Ovaj elementarni postupak zapravo znači sljedeće: pravi objekt (ploha stola) zamjenjuje se apstraktnim matematičkim modelom – pravokutnikom. Dimenzije dobivene mjerenjem dužine i širine površine stola dodjeljuju se pravokutniku, a površina takvog pravokutnika se približno uzima kao potrebna površina stola. Međutim, model pravougaonika za radni sto je najjednostavniji, najgrublji model. Ako ozbiljnije pristupite problemu, prije korištenja modela pravokutnika za određivanje površine stola, ovaj model treba provjeriti. Provjere se mogu izvršiti na sljedeći način: izmjerite dužine suprotnih strana stola, kao i dužine njegovih dijagonala i uporedite ih međusobno. Ako su, uz traženi stepen tačnosti, dužine suprotnih strana i dužine dijagonala jednake u parovima, tada se površina stola zaista može smatrati pravougaonikom. U suprotnom, model pravokutnika će se morati odbaciti i zamijeniti općim modelom četverougla. Uz veći zahtjev za preciznošću, možda će biti potrebno dodatno precizirati model, na primjer, da se uzme u obzir zaokruživanje uglova stola.

Koristeći ovaj jednostavan primjer, pokazalo se da matematički model nije jednoznačno određen objektom, procesom ili sistem.

ILI (razjašnjenje sutra)

Načini rješavanja matematike. modeli:

1, Izgradnja modela zasnovanog na zakonima prirode (analitička metoda)

2. Formalni način korištenjem statističkih metoda. Obrada i rezultati mjerenja (statistički pristup)

3. Izgradnja modela na osnovu modela elemenata (složenih sistema)

1, Analitički - koristiti uz dovoljno proučavanja. Opšti obrazac je poznat. Modeli.

2. eksperiment. U nedostatku informacija.

3. Imitacija m. - istražuje svojstva predmeta. Generalno.

Primjer konstruiranja matematičkog modela.

Matematički model je matematički prikaz stvarnosti.

Matematičko modeliranje je proces konstruisanja i proučavanja matematičkih modela.

Sve prirodne i društvene nauke koje koriste matematiku u suštini se bave matematičkim modeliranjem: zamenjuju objekat njegovim matematičkim modelom, a zatim ga proučavaju. Veza između matematičkog modela i stvarnosti ostvaruje se pomoću lanca hipoteza, idealizacija i pojednostavljenja. Matematičkim metodama se po pravilu opisuje idealan objekat konstruisan u fazi smislenog modeliranja.

Zašto su potrebni modeli?

Vrlo često, prilikom proučavanja bilo kojeg objekta, nastaju poteškoće. Sam original je ponekad nedostupan, ili njegova upotreba nije preporučljiva, ili je privlačenje originala skupo. Svi ovi problemi se mogu riješiti simulacijom. U određenom smislu, model može zamijeniti predmet koji se proučava.

Najjednostavniji primjeri modela

§ Fotografija se može nazvati modelom osobe. Da biste prepoznali osobu, dovoljno je vidjeti njegovu fotografiju.

§ Arhitekta je izradio model novog stambenog prostora. Pokretom ruke može premjestiti višespratnicu iz jednog dijela u drugi. U stvarnosti to ne bi bilo moguće.

Tipovi modela

Modeli se mogu podijeliti na materijal" I savršeno. gornji primjeri su materijalni modeli. Idealni modeli često imaju ikonične oblike. Pravi pojmovi su zamijenjeni nekim znacima, koji se lako mogu zabilježiti na papiru, u memoriji računala itd.

Matematičko modeliranje

Matematičko modeliranje pripada klasi simboličkog modeliranja. Štoviše, modeli se mogu kreirati iz bilo kojeg matematičkog objekta: brojeva, funkcija, jednadžbi itd.

Izgradnja matematičkog modela

§ Može se uočiti nekoliko faza konstruisanja matematičkog modela:

1. Razumijevanje problema, identificiranje najvažnijih kvaliteta, svojstava, količina i parametara za nas.

2. Uvođenje notacije.

3. Izrada sistema ograničenja koje unesene vrijednosti moraju zadovoljiti.

4. Formulisanje i evidentiranje uslova koje mora zadovoljiti željeno optimalno rešenje.

Proces modeliranja se ne završava stvaranjem modela, već njime tek počinje. Nakon što su sastavili model, biraju metodu za pronalaženje odgovora i rješavanje problema. nakon što se nađe odgovor, on se upoređuje sa stvarnošću. I moguće je da odgovor nije zadovoljavajući, u tom slučaju se model modificira ili čak bira potpuno drugačiji model.

Primjer matematičkog modela

Zadatak

Proizvodno udruženje, koje uključuje dvije fabrike namještaja, treba da ažurira svoj mašinski park. Štaviše, prva fabrika nameštaja treba da zameni tri mašine, a druga sedam. Narudžbe se mogu izvršiti u dvije fabrike alatnih mašina. Prvi pogon može proizvesti najviše 6 mašina, a drugi će prihvatiti narudžbu ako ih ima najmanje tri. Morate odrediti način narudžbe.

Primjer 1.5.1.

Neka određena privredna regija proizvodi nekoliko (n) vrsta proizvoda isključivo samostalno i samo za stanovništvo ove regije. Pretpostavlja se da je tehnološki proces razrađen, te da je proučena potražnja stanovništva za ovom robom. Potrebno je odrediti godišnji obim proizvodnje proizvoda, uzimajući u obzir činjenicu da taj obim mora obezbijediti i finalnu i industrijsku potrošnju.

Hajde da napravimo matematički model ovog problema. Prema njegovim uslovima daju se: vrste proizvoda, potražnja za njima i tehnološki proces; morate pronaći izlazni volumen svake vrste proizvoda.

Označimo poznate veličine:

c i– potražnja stanovništva za i ti proizvod ( i=1,...,n); a ij- količina i th proizvod potreban za proizvodnju jedinice j-tog proizvoda koristeći datu tehnologiju ( i=1,...,n ; j=1,...,n);

X i – izlazni volumen i-ti proizvod ( i=1,...,n); totalitet With =(c 1 ,..., c n ) koji se nazivaju vektor potražnje, brojevi a ij– tehnološki koeficijenti, i ukupno X =(X 1 ,..., X n ) – vektor oslobađanja.

Prema uslovima problema, vektor X raspoređeni u dva dijela: za krajnju potrošnju (vektor With ) i za reprodukciju (vektor x-s ). Izračunajmo taj dio vektora X koji ide u reprodukciju. Prema našim oznakama za proizvodnju X j količina isporučenog j-tog proizvoda a ij · X j količine i-ti proizvod.

Zatim iznos a i1 · X 1 +...+ a in · X n pokazuje tu vrijednost i-ti proizvod, koji je potreban za cijelo izdanje X =(X 1 ,..., X n ).

Dakle, jednakost mora biti zadovoljena:

Proširujući ovo razmišljanje na sve vrste proizvoda, dolazimo do željenog modela:

Rješavanje ovog sistema od n linearnih jednačina za X 1 ,...,X n i pronađite traženi vektor oslobađanja.

Da bismo ovaj model zapisali u kompaktnijem (vektorskom) obliku, uvodimo sljedeću notaciju:

Kvadrat (
) -matrica A nazvana tehnološka matrica. Lako je provjeriti da će naš model sada biti napisan ovako: x-s=Ah ili

(1.6)

Dobili smo klasični model" Ulaz - Izlaz “, čiji je autor poznati američki ekonomista V. Leontiev.

Primjer 1.5.2.

Rafinerija nafte ima dvije vrste nafte: kvalitet A u količini od 10 jedinica, ocjena IN- 15 jedinica. Prilikom prerade nafte dobijaju se dva materijala: benzin (označavamo B) i lož ulje ( M). Postoje tri opcije za proces tehnologije obrade:

I: 1 kom A+ 2 jedinice IN daje 3 jedinice. B+ 2 jedinice M

II: 2 jedinice. A+ 1 jedinica IN daje 1 jedinicu. B+ 5 jedinica M

III: 2 kom A+ 2 jedinice IN daje 1 jedinicu. B+ 2 jedinice M

Cijena benzina je 10 USD po jedinici, lož ulja 1 USD po jedinici.

Potrebno je odrediti najpovoljniju kombinaciju tehnoloških procesa za preradu raspoložive količine nafte.

Prije modeliranja, razjasnimo sljedeće točke. Iz uslova problema proizilazi da „isplativost“ tehnološkog procesa za postrojenje treba shvatiti u smislu ostvarivanja maksimalnog prihoda od prodaje njegovih gotovih proizvoda (benzina i lož ulja). S tim u vezi, jasno je da se „odluka o izboru (donošenju)“ postrojenja sastoji u određivanju koju će tehnologiju primijeniti i koliko puta. Očigledno, takvih mogućih opcija ima dosta.

Označimo nepoznate veličine:

X i– količina upotrebe i tehnološki proces (i=1,2,3). Ostali parametri modela (zalihe nafte, cijene benzina i lož ulja) poznato.

Sada se jedna konkretna odluka o biljci svodi na odabir jednog vektora X =(x 1 ,X 2 ,X 3 ) , za koji je prihod fabrike jednak (32x 1 +15x 2 +12x 3 ) Ovdje je 32 dolara prihod od jedne primjene prvog tehnološkog procesa ($10 3 jedinice. B+ 1 dolar ·2 jedinice. M= 32 USD). Koeficijenti 15 i 12 za drugi i treći tehnološki proces, respektivno, imaju slično značenje. Obračun rezervi nafte dovodi do sljedećih uslova:

za raznolikost A:

za raznolikost IN:,

gdje su u prvoj nejednakosti koeficijenti 1, 2, 2 stope potrošnje ulja razreda A za jednokratnu upotrebu tehnoloških procesa I,II,III respektivno. Koeficijenti druge nejednakosti imaju slično značenje za ulje klase B.

Matematički model u cjelini ima oblik:

Pronađite takav vektor x = (x 1 ,X 2 ,X 3 ) maksimizirati

f(x) =32h 1 +15x 2 +12x 3

pod sljedećim uslovima:

Skraćeni oblik ovog unosa je:

pod ograničenjima

(1.7)

Dobili smo takozvani problem linearnog programiranja.

Model (1.7.) je primjer optimizacijskog modela determinističkog tipa (sa dobro definiranim elementima).

Primjer 1.5.3.

Investitor treba da odredi najbolju kombinaciju dionica, obveznica i drugih vrijednosnih papira za kupovinu za određeni iznos kako bi ostvario određeni profit uz minimalan rizik za sebe. Profit po dolaru uloženom u hartiju od vrijednosti j- vrsta, koju karakterišu dva indikatora: očekivana dobit i stvarna dobit. Za investitora je poželjno da očekivana dobit po dolaru ulaganja ne bude niža od zadate vrednosti za ceo set hartija od vrednosti b.

Imajte na umu da se za pravilno modeliranje ovog problema od matematičara traži određena osnovna znanja iz oblasti portfolio teorije hartija od vrijednosti.

Označimo poznate parametre problema:

n– broj vrsta hartija od vrijednosti; A j– stvarni profit (slučajni broj) od j-te vrste hartije od vrijednosti; – očekivana dobit od j-th vrsta obezbeđenja.

Označimo nepoznate veličine :

y j - sredstva namijenjena za kupovinu hartija od vrijednosti ove vrste j.

Koristeći našu notaciju, cjelokupni uloženi iznos se izražava kao . Da bismo pojednostavili model, uvodimo nove količine

dakle, X i- ovo je udio svih sredstava namijenjenih za sticanje hartija od vrijednosti ovog tipa j.

To je jasno

Iz uslova problema jasno je da je cilj investitora da uz minimalan rizik postigne određeni nivo profita. U suštini, rizik je mjera odstupanja stvarne dobiti od očekivane. Stoga se može poistovetiti sa kovarijansom dobiti za hartije od vrednosti tipa i i tipa j. Ovdje je M oznaka matematičkog očekivanja.

Matematički model originalnog problema ima oblik:

pod ograničenjima

,
,
,
. (1.8)

Dobili smo poznati Markowitz model za optimizaciju strukture portfelja hartija od vrijednosti.

Model (1.8.) je primjer optimizacijskog modela stohastičkog tipa (sa elementima slučajnosti).

Primjer 1.5.4.

Na osnovu trgovinske organizacije postoji n vrsta jednog od proizvoda minimalnog asortimana. U prodavnicu se mora unijeti samo jedna vrsta datog proizvoda. Morate odabrati vrstu proizvoda koju je prikladno unijeti u trgovinu. Ako je tip proizvoda jće biti tražena, prodavnica će ostvariti profit od svoje prodaje R j, ako nije tražena - gubitak q j .

Prije modeliranja, razmotrit ćemo neke osnovne točke. U ovom problemu, donosilac odluke (DM) je prodavnica. Međutim, ishod (maksimalni profit) ne zavisi samo od njegove odluke, već i od toga da li će uvezeni proizvod biti tražen, odnosno da li će ga kupovati stanovništvo (pretpostavlja se da prodavnica iz nekog razloga ne imaju priliku da proučavaju potražnju stanovništva). Stoga se stanovništvo može smatrati drugim donosiocem odluka, birajući vrstu proizvoda prema svojim preferencijama. Najgora “odluka” stanovništva za radnju je: “uvezena roba nije tražena”. Dakle, da bi se uzele u obzir sve moguće situacije, trgovina mora smatrati stanovništvo svojim "neprijateljem" (uvjetno), slijedeći suprotan cilj - minimizirati profit trgovine.

Dakle, imamo problem donošenja odluka sa dva učesnika koji teže suprotnim ciljevima. Pojasnimo da prodavnica bira jednu od vrsta robe za prodaju (postoji n opcija odluke), a stanovništvo bira jednu od vrsta robe za kojom je najveća potražnja ( n opcije rješenja).

Da bismo sastavili matematički model, nacrtajmo tabelu sa n linije i n kolone (ukupno n 2 ćelije) i slažu se da redovi odgovaraju izboru prodavnice, a kolone izboru populacije. Zatim ćelija (i, j) odgovara situaciji kada prodavnica izabere i ta vrsta proizvoda ( i-ti red), a stanovništvo bira j ta vrsta proizvoda ( j- kolona). U svaku ćeliju upisujemo numeričku procjenu (dobit ili gubitak) odgovarajuće situacije sa stanovišta trgovine:

Brojevi q i napisano sa minusom da odražava gubitak prodavnice; u svakoj situaciji, “dobitak” populacije (uslovno) jednak je “dobitku” trgovine, uzet sa suprotnim predznakom.

Skraćeni oblik ovog modela je:

(1.9)