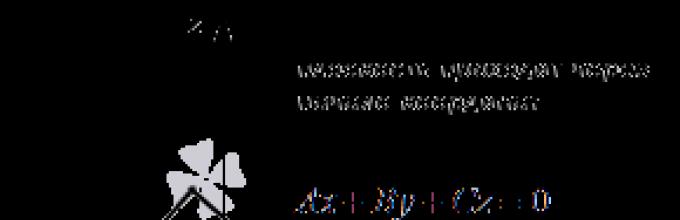
Ako su svi brojevi A, B, C i D različiti od nule, onda se opšta jednačina ravnine naziva kompletan. Inače, naziva se opšta jednačina ravni nepotpuna.

Razmotrimo sve moguće zajedničke nepotpune jednačine ravan u pravougaonom Oxyz koordinatnom sistemu u trodimenzionalnom prostoru.

Neka je D = 0, tada imamo opštu nepotpunu ravan jednadžbinu oblika . Ova ravan u pravougaonom koordinatnom sistemu Oxyz prolazi kroz ishodište. Zaista, kada zamenimo koordinate tačke u rezultirajuću nepotpunu jednačinu ravni, dolazimo do identiteta .


Za , ili , ili imamo opće nepotpune jednadžbe ravnina , ili , ili , respektivno. Ove jednadžbe definiraju ravnine paralelne sa koordinatnim ravninama Oxy, Oxz i Oyz, redom (vidi članak za stanje paralelnih ravnina) i prolaze kroz tačke i shodno tome. At. Od tačke pripada ravni po uslovu, tada koordinate ove tačke moraju zadovoljiti jednačinu ravni, odnosno jednakost mora biti tačna. Odavde nalazimo. Dakle, tražena jednačina ima oblik .

Predstavimo drugi način rješavanja ovog problema.

Kako je ravan, čiju opštu jednačinu treba da sastavimo, paralelna ravni Oyz, onda kao njen vektor normale možemo uzeti vektor normale ravni Oyz. Normalni vektor koordinatna ravan Oyz je koordinatni vektor. Sada znamo vektor normale ravnine i tačku ravnine, stoga možemo napisati njenu opštu jednačinu (sličan problem smo riješili u prethodnom pasusu ovog članka):
, tada njegove koordinate moraju zadovoljiti jednadžbu ravnine. Dakle, jednakost je tačna odakle ga nalazimo. Sada možemo napisati željenu opštu jednačinu ravnine, ona ima oblik .

odgovor:

Bibliografija.

  • Bugrov Ya.S., Nikolsky S.M. Viša matematika. Prvi tom: Elementi linearna algebra i analitičku geometriju.
  • Ilyin V.A., Poznyak E.G. Analitička geometrija.

Može se specificirati na različite načine (jedna tačka i vektor, dve tačke i vektor, tri tačke itd.). Imajući to na umu, jednadžba ravni može imati različite oblike. Takođe, pod određenim uslovima, ravni mogu biti paralelne, okomite, ukrštane, itd. O tome ćemo razgovarati u ovom članku. Naučit ćemo kako napraviti opštu jednadžbu ravnine i još mnogo toga.

Normalan oblik jednačine

Recimo da postoji prostor R 3 koji ima pravougaoni XYZ koordinatni sistem. Definirajmo vektor α, koji će biti oslobođen iz početne tačke O. Kroz kraj vektora α povlačimo ravan P, koja će biti okomita na nju.

Označimo proizvoljnu tačku na P kao Q = (x, y, z). Označimo radijus vektor tačke Q slovom p. U ovom slučaju, dužina vektora α je jednaka r=IαI i Ʋ=(cosα,cosβ,cosγ).

Ovo je jedinični vektor koji je usmjeren u stranu, poput vektora α. α, β i γ su uglovi koji se formiraju između vektora Ʋ i pozitivnih pravaca prostornih osa x, y, z, redom. Projekcija bilo koje tačke QϵP na vektor Ʋ je konstantna vrijednost koja je jednaka p: (p,Ʋ) = p(p≥0).

Gornja jednadžba ima smisla kada je p=0. Jedino što će ravan P u ovom slučaju preseći tačku O (α=0), koja je ishodište koordinata, a jedinični vektor Ʋ oslobođen iz tačke O će biti okomit na P, uprkos svom pravcu, koji znači da je vektor Ʋ određen s točnošću predznaka. Prethodna jednačina je jednačina naše ravni P, izražena u vektorskom obliku. Ali u koordinatama to će izgledati ovako:

P je ovdje veće ili jednako 0. Pronašli smo jednadžbu ravnine u prostoru u normalnom obliku.

Opšta jednačina

Ako pomnožimo jednačinu u koordinatama bilo kojim brojem koji nije jednak nuli, dobićemo jednačinu koja je ekvivalentna ovoj, koja definira upravo tu ravan. To će izgledati ovako:

Ovdje su A, B, C brojevi koji su istovremeno različiti od nule. Ova jednačina se zove opšta ravan jednačina.

Jednačine ravnina. Posebni slučajevi

Jednačina u opštem obliku može se modificirati ako postoji dodatni uslovi. Pogledajmo neke od njih.

Pretpostavimo da je koeficijent A 0. To znači da je ova ravan paralelna sa datom Ox osom. U ovom slučaju, oblik jednačine će se promijeniti: Vu+Cz+D=0.

Slično, oblik jednačine će se promijeniti pod sljedećim uvjetima:

  • Prvo, ako je B = 0, tada će se jednadžba promijeniti u Ax + Cz + D = 0, što će ukazati na paralelizam s Oy osom.
  • Drugo, ako je C=0, tada će jednačina biti transformisana u Ax+By+D=0, što će ukazati na paralelizam sa datom Oz osom.
  • Treće, ako je D=0, jednačina će izgledati kao Ax+By+Cz=0, što će značiti da ravan seče O (početak).
  • Četvrto, ako je A=B=0, tada će se jednačina promijeniti u Cz+D=0, što će se pokazati paralelnim sa Oxy.
  • Peto, ako je B=C=0, onda jednačina postaje Ax+D=0, što znači da je ravan na Oyz paralelna.
  • Šesto, ako je A=C=0, tada će jednadžba dobiti oblik Vu+D=0, to jest, ona će izvesti paralelizam Oxz.

Tip jednadžbe u segmentima

U slučaju kada su brojevi A, B, C, D različiti od nule, oblik jednačine (0) može biti sljedeći:

x/a + y/b + z/c = 1,

u kojoj je a = -D/A, b = -D/B, c = -D/C.

Dobijamo kao rezultat.Vrijedi napomenuti da će ova ravan presjeći osu Ox u tački s koordinatama (a,0,0), Oy - (0,b,0) i Oz - (0,0,c ).

Uzimajući u obzir jednačinu x/a + y/b + z/c = 1, nije teško vizuelno zamisliti položaj ravni u odnosu na dati koordinatni sistem.

Normalne vektorske koordinate

Vektor normale n na ravan P ima koordinate koje su koeficijenti opšta jednačina date ravni, odnosno n (A, B, C).

Da bi se odredile koordinate normale n, dovoljno je poznavati opštu jednačinu date ravni.

Kada koristite jednadžbu u segmentima, koja ima oblik x/a + y/b + z/c = 1, kao i kada koristite opštu jednačinu, možete napisati koordinate bilo kojeg vektora normale date ravni: (1 /a + 1/b + 1/ sa).

Vrijedi napomenuti da normalni vektor pomaže u rješavanju raznih problema. Najčešći su problemi koji uključuju dokazivanje okomitosti ili paralelnosti ravnina, problemi nalaženja uglova između ravnina ili uglova između ravnina i pravih.

Vrsta ravnine jednadžbe prema koordinatama tačke i vektora normale

Vektor različit od nule n okomit na datu ravan naziva se normalan za datu ravan.

Pretpostavimo da je u koordinatni prostor(pravougaoni koordinatni sistem) Oxyz su dati:

  • tačka Mₒ sa koordinatama (xₒ,yₒ,zₒ);
  • nulti vektor n=A*i+B*j+C*k.

Potrebno je napraviti jednačinu za ravan koja će prolaziti kroz tačku Mₒ okomito na normalu n.

Biramo bilo koju proizvoljnu tačku u prostoru i označavamo je M (x y, z). Neka je vektor radijusa bilo koje tačke M (x,y,z) r=x*i+y*j+z*k, a vektor radijusa tačke Mₒ (xₒ,yₒ,zₒ) - rₒ=xₒ* i+yₒ *j+zₒ*k. Tačka M će pripadati datoj ravni ako je vektor MₒM okomit na vektor n. Zapišimo uvjet ortogonalnosti koristeći skalarni proizvod:

[MₒM, n] = 0.

Kako je MₒM = r-rₒ, vektorska jednadžba ravni će izgledati ovako:

Ova jednačina može imati i drugi oblik. Za to se koriste svojstva skalarnog proizvoda, a lijeva strana jednadžbe se transformira. = - . Ako ga označimo sa c, dobijamo sljedeću jednačinu: - c = 0 ili = c, koja izražava konstantnost projekcija na vektor normale vektora radijusa datih tačaka koje pripadaju ravni.

Sada možete dobiti koordinatni prikaz zapisa vektorska jednadžba naša ravan = 0. Pošto je r-rₒ = (x-xₒ)*i + (y-yₒ)*j + (z-zₒ)*k, i n = A*i+B*j+C*k, mi imamo:

Ispada da imamo jednadžbu za ravan koja prolazi kroz tačku okomitu na normalu n:

A*(x- xₒ)+B*(y- yₒ)C*(z-zₒ)=0.

Tip ravnine jednadžbe prema koordinatama dvije tačke i vektora kolinearnog ravni

Navedite dvije proizvoljne tačke M′ (x′,y′,z′) i M″ (x″,y″,z″), kao i vektor a (a′,a″,a‴).

Sada možemo kreirati jednačinu za datu ravan koja će prolaziti kroz postojeće tačke M′ i M″, kao i bilo koju tačku M sa koordinatama (x, y, z) paralelnim sa datim vektorom a.

U ovom slučaju, vektori M′M=(x-x′;y-y′;z-z′) i M″M=(x″-x′;y″-y′;z″-z′) moraju biti komplanarni sa vektorom a=(a′,a″,a‴), što znači da je (M′M, M″M, a)=0.

Dakle, naša jednačina ravnine u prostoru će izgledati ovako:

Vrsta jednačine ravnine koja seče tri tačke

Recimo da imamo tri tačke: (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴), koje ne pripadaju istoj pravoj. Potrebno je napisati jednačinu ravni koja prolazi kroz date tri tačke. Teorija geometrije tvrdi da ova vrsta ravni zaista postoji, ali je jedina i jedinstvena. Pošto ova ravan siječe tačku (x′,y′,z′), oblik njene jednadžbe će biti sljedeći:

Ovdje se A, B, C razlikuju od nule u isto vrijeme. Takođe, data ravan seče još dve tačke: (x″,y″,z″) i (x‴,y‴,z‴). U tom smislu moraju biti ispunjeni sljedeći uslovi:

Sada možemo kreirati homogeni sistem sa nepoznatim u, v, w:

U našem slučaj x,y ili z djeluje kao proizvoljna tačka koja zadovoljava jednačinu (1). S obzirom na jednačinu (1) i sistem jednačina (2) i (3), sistem jednačina prikazan na gornjoj slici zadovoljava vektor N (A,B,C), koji nije trivijalan. Zbog toga je determinanta ovog sistema jednaka nuli.

Jednačina (1) koju smo dobili je jednačina ravnine. Prolazi tačno kroz 3 tačke i to je lako provjeriti. Da bismo to učinili, moramo proširiti našu determinantu na elemente u prvom redu. Iz postojećih svojstava determinante proizilazi da naša ravan istovremeno siječe tri početno date tačke (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴) . Odnosno, riješili smo zadatak koji nam je dodijeljen.

Diedarski ugao između ravnina

Diedarski ugao predstavlja prostorni geometrijska figura, formiran od dvije poluravnine koje izlaze iz jedne prave linije. Drugim riječima, ovo je dio prostora koji je ograničen ovim poluravnima.

Recimo da imamo dvije ravni sa sljedećim jednadžbama:

Znamo da su vektori N=(A,B,C) i N¹=(A¹,B¹,C¹) okomiti prema dati avioni. U tom smislu, ugao φ između vektora N i N¹ jednak je uglu (diedralu) koji se nalazi između ovih ravni. Tačkasti proizvod ima oblik:

NN¹=|N||N¹|cos φ,

upravo zato

cosφ= NN¹/|N||N¹|=(AA¹+BB¹+CC¹)/((√(A²+B²+C²))*(√(A¹)²+(B¹)²+(C¹)²)).

Dovoljno je uzeti u obzir da je 0≤φ≤π.

Zapravo, dvije ravni koje se seku formiraju dva ugla (diedral): φ 1 i φ 2. Njihov zbir je jednak π (φ 1 + φ 2 = π). Što se tiče njihovih kosinusa, njihove apsolutne vrijednosti su jednake, ali se razlikuju po predznaku, odnosno cos φ 1 = -cos φ 2. Ako u jednačini (0) zamijenimo A, B i C brojevima -A, -B i -C, redom, tada će jednačina koju dobijemo odrediti istu ravan, jedinu, ugao φ u jednačini cos φ= NN 1 /|N||N 1 | će biti zamijenjen sa π-φ.

Jednadžba okomite ravni

Ravnine između kojih je ugao od 90 stepeni nazivaju se okomite. Koristeći gore predstavljeni materijal, možemo pronaći jednadžbu ravnine koja je okomita na drugu. Recimo da imamo dvije ravni: Ax+By+Cz+D=0 i A¹x+B¹y+C¹z+D=0. Možemo reći da će biti okomite ako je cosφ=0. To znači da je NN¹=AA¹+BB¹+CC¹=0.

Jednačina paralelne ravni

Dvije ravni koje ne sadrže zajedničke tačke nazivaju se paralelne.

Uslov (njihove jednačine su iste kao u prethodnom paragrafu) je da su vektori N i N¹, koji su okomiti na njih, kolinearni. To znači da su ispunjeni sljedeći uvjeti proporcionalnosti:

A/A¹=B/B¹=C/C¹.

Ako su uslovi proporcionalnosti prošireni - A/A¹=B/B¹=C/C¹=DD¹,

ovo ukazuje da se ove ravni poklapaju. To znači da jednačine Ax+By+Cz+D=0 i A¹x+B¹y+C¹z+D¹=0 opisuju jednu ravan.

Udaljenost do ravnine od tačke

Recimo da imamo ravan P, koja je data jednačinom (0). Potrebno je pronaći udaljenost do nje od tačke sa koordinatama (xₒ,yₒ,zₒ)=Qₒ. Da biste to učinili, trebate dovesti jednadžbu ravnine P u normalan oblik:

(ρ,v)=r (r≥0).

U ovom slučaju, ρ (x,y,z) je vektor radijusa naše tačke Q koja se nalazi na P, p je dužina okomice P koja je oslobođena od nulte tačke, v je jedinični vektor, koji se nalazi u smjer a.

Vektor radijusa razlike ρ-ρº neke tačke Q = (x, y, z), koja pripada P, kao i vektor radijusa date tačke Q 0 = (xₒ, yₒ, zₒ) je takav vektor, apsolutna vrijednostčija je projekcija na v jednaka udaljenosti d, koju treba naći od Q 0 = (xₒ,uₒ,zₒ) do P:

D=|(ρ-ρ 0 ,v)|, ali

(ρ-ρ 0 ,v)= (ρ,v)-(ρ 0 ,v) =r-(ρ 0 ,v).

Tako se ispostavilo

d=|(ρ 0 ,v)-r|.

Tako ćemo naći apsolutnu vrijednost rezultirajućeg izraza, odnosno željeni d.

Koristeći jezik parametara, dobijamo očigledno:

d=|Ahₒ+Vuₒ+Czₒ|/√(A²+V²+S²).

Ako set lopta Q 0 je na drugoj strani ravni P, kao i ishodište koordinata, tada se između vektora ρ-ρ 0 i v nalazi:

d=-(ρ-ρ 0 ,v)=(ρ 0 ,v)-r>0.

U slučaju kada se tačka Q 0, zajedno sa ishodištem koordinata, nalazi na istoj strani od P, tada je stvoreni ugao oštar, odnosno:

d=(ρ-ρ 0 ,v)=r - (ρ 0 , v)>0.

Kao rezultat toga, ispada da je u prvom slučaju (ρ 0 ,v)>r, u drugom (ρ 0 ,v)<р.

Tangentna ravan i njena jednadžba

Tangentna ravan na površinu u tački kontakta Mº je ravan koja sadrži sve moguće tangente na krivulje povučene kroz ovu tačku na površini.

Sa ovom vrstom površinske jednačine F(x,y,z)=0, jednačina tangentne ravni u tački tangente Mº(xº,yº,zº) će izgledati ovako:

F x (xº,yº,zº)(x- xº)+ F x (xº, yº, zº)(y- yº)+ F x (xº, yº,zº)(z-zº)=0.

Ako zadate površinu u eksplicitnom obliku z=f (x,y), tada će tangentna ravan biti opisana jednadžbom:

z-zº =f(xº, yº)(x- xº)+f(xº, yº)(y- yº).

Presjek dvije ravni

U koordinatnom sistemu (pravougaonom) nalazi se Oxyz, date su dve ravni P′ i P″ koje se seku i ne poklapaju. Pošto je bilo koja ravan koja se nalazi u pravougaonom koordinatnom sistemu određena opštom jednačinom, pretpostavićemo da su P′ i P″ date jednačinama A′x+B′y+C′z+D′=0 i A″x +B″y+ S″z+D″=0. U ovom slučaju imamo normalu n′ (A′,B′,C′) ravni P′ i normalu n″ (A″,B″,C″) ravni P″. Pošto naše ravni nisu paralelne i ne poklapaju se, ovi vektori nisu kolinearni. Koristeći jezik matematike, ovaj uslov možemo napisati na sljedeći način: n′≠ n″ ↔ (A′,B′,C′) ≠ (λ*A″,λ*B″,λ*C″), λϵR. Neka prava linija koja leži na raskrsnici P′ i P″ bude označena slovom a, u ovom slučaju a = P′ ∩ P″.

a je prava linija koja se sastoji od skupa svih tačaka (zajedničkih) ravni P′ i P″. To znači da koordinate bilo koje tačke koja pripada pravoj a moraju istovremeno zadovoljiti jednačine A′x+B′y+C′z+D′=0 i A″x+B″y+C″z+D″=0 . To znači da će koordinate tačke biti djelomično rješenje sljedećeg sistema jednačina:

Kao rezultat toga, ispada da će (opće) rješenje ovog sistema jednadžbi odrediti koordinate svake od tačaka prave, koja će djelovati kao presječna tačka P′ i P″, i odrediti pravu liniju a u Oxyz (pravougaonom) koordinatnom sistemu u prostoru.

Svojstva prave linije u euklidskoj geometriji.

Kroz bilo koju tačku može se povući beskonačan broj pravih linija.

Kroz bilo koje dvije tačke koje se ne poklapaju može se povući jedna prava linija.

Dvije divergentne prave u ravni ili se sijeku u jednoj tački ili su

paralelno (slijedi iz prethodnog).

U trodimenzionalnom prostoru postoje tri opcije za relativni položaj dvije linije:

  • linije se seku;
  • prave su paralelne;
  • prave se seku.

Pravo linija— algebarska kriva prvog reda: prava linija u Dekartovom koordinatnom sistemu

je dato na ravni jednačinom prvog stepena (linearna jednačina).

Opšta jednačina prave linije.

Definicija. Bilo koja prava linija na ravni može se odrediti jednadžbom prvog reda

Ax + Wu + C = 0,

i konstantan A, B nisu jednake nuli u isto vrijeme. Ova jednačina prvog reda se zove general

jednačina prave linije. Ovisno o vrijednostima konstanti A, B I WITH Mogući su sljedeći posebni slučajevi:

. C = 0, A ≠0, B ≠ 0- prava linija prolazi kroz ishodište

. A = 0, B ≠0, C ≠0 (By + C = 0)- prava paralelna sa osom Oh

. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- prava paralelna sa osom OU

. B = C = 0, A ≠0- prava linija se poklapa sa osom OU

. A = C = 0, B ≠0- prava linija se poklapa sa osom Oh

Jednačina prave linije može se predstaviti u različitim oblicima u zavisnosti od bilo koje date

početni uslovi.

Jednačina prave linije iz tačke i vektora normale.

Definicija. U kartezijanskom pravougaonom koordinatnom sistemu, vektor sa komponentama (A, B)

okomito na pravu datu jednacinom

Ax + Wu + C = 0.

Primjer. Naći jednačinu prave koja prolazi kroz tačku A(1, 2) okomito na vektor (3, -1).

Rješenje. Sa A = 3 i B = -1, sastavimo jednačinu prave linije: 3x - y + C = 0. Da pronađemo koeficijent C

Zamenimo koordinate date tačke A u rezultirajući izraz. Dobijamo: 3 - 2 + C = 0, dakle

C = -1. Ukupno: tražena jednačina: 3x - y - 1 = 0.

Jednadžba prave koja prolazi kroz dvije tačke.

Neka su u prostoru date dvije tačke M 1 (x 1 , y 1 , z 1) I M2 (x 2, y 2, z 2), Onda jednačina prave,

prolazeći kroz ove tačke:

Ako je bilo koji od nazivnika nula, odgovarajući brojnik treba postaviti jednak nuli. On

ravni, jednadžba ravne linije koja je gore napisana je pojednostavljena:

Ako x 1 ≠ x 2 I x = x 1, Ako x 1 = x 2 .

Razlomak = k pozvao nagib ravno.

Primjer. Naći jednačinu prave koja prolazi kroz tačke A(1, 2) i B(3, 4).

Rješenje. Primjenom gore napisane formule dobijamo:

Jednadžba prave linije koristeći tačku i nagib.

Ako je opća jednačina prave Ax + Wu + C = 0 voditi do:

i odrediti , tada se rezultirajuća jednačina zove

jednačina prave linije sa nagibom k.

Jednačina prave linije iz tačke i vektora pravca.

Po analogiji sa tačkom koja razmatra jednadžbu prave linije kroz vektor normale, možete ući u zadatak

prava linija kroz tačku i usmjeravajući vektor prave linije.

Definicija. Svaki vektor različit od nule (α 1 , α 2), čije komponente zadovoljavaju uslov

Aα 1 + Bα 2 = 0 pozvao usmjeravajući vektor prave linije.

Ax + Wu + C = 0.

Primjer. Naći jednačinu prave sa vektorom pravca (1, -1) i koja prolazi kroz tačku A(1, 2).

Rješenje. Tražit ćemo jednadžbu željene linije u obliku: Ax + By + C = 0. prema definiciji,

koeficijenti moraju zadovoljiti sljedeće uslove:

1 * A + (-1) * B = 0, tj. A = B.

Tada jednačina prave linije ima oblik: Ax + Ay + C = 0, ili x + y + C / A = 0.

at x = 1, y = 2 dobijamo C/A = -3, tj. tražena jednačina:

x + y - 3 = 0

Jednačina prave linije u segmentima.

Ako je u opštoj jednačini prave Ah + Vu + S = 0 S≠0, onda, dijeljenjem sa -S, dobijamo:

ili gde

Geometrijsko značenje koeficijenata je da je koeficijent a koordinata tačke preseka

ravno sa osom Oh, A b- koordinata tačke preseka linije sa osom OU.

Primjer. Daje se opšta jednačina prave linije x - y + 1 = 0. Naći jednačinu ove prave u segmentima.

C = 1, , a = -1, b = 1.

Normalna jednadžba prave.

Ako obje strane jednačine Ax + Wu + C = 0 podijeliti brojem koji se zove

normalizujući faktor, onda dobijamo

xcosφ + ysinφ - p = 0 -normalna jednačina prave.

Predznak ± faktora normalizacije mora biti odabran tako da μ*C< 0.

R- dužina okomice spuštena od početka do prave linije,

A φ - ugao koji formira ova okomita sa pozitivnim smjerom ose Oh.

Primjer. Daje se opšta jednačina prave 12x - 5y - 65 = 0. Potrebno za pisanje različitih vrsta jednačina

ovu pravu liniju.

Jednačina ove prave u segmentima:

Jednačina ove prave sa nagibom: (podijeliti sa 5)

Jednačina prave:

cos φ = 12/13; sin φ= -5/13; p = 5.

Treba napomenuti da se ne može svaka prava linija predstaviti jednadžbom u segmentima, na primjer, prave,

paralelno sa osama ili prolazeći kroz ishodište.

Ugao između pravih linija na ravni.

Definicija. Ako su data dva reda y = k 1 x + b 1 , y = k 2 x + b 2, zatim oštar ugao između ovih linija

će se definisati kao

Dvije prave su paralelne ako k 1 = k 2. Dvije prave su okomite

Ako k 1 = -1/ k 2 .

Teorema.

Direktno Ax + Wu + C = 0 I A 1 x + B 1 y + C 1 = 0 paralelno kada su koeficijenti proporcionalni

A 1 = λA, B 1 = λB. Ako takođe S 1 = λS, tada se linije poklapaju. Koordinate tačke preseka dve prave

nalaze se kao rješenje sistema jednačina ovih linija.

Jednačina prave koja prolazi kroz datu tačku okomito na datu pravu.

Definicija. Prava koja prolazi kroz tačku M 1 (x 1, y 1) i okomito na pravu y = kx + b

predstavljena jednačinom:

Udaljenost od tačke do prave.

Teorema. Ako je dat poen M(x 0, y 0), zatim udaljenost do prave linije Ax + Wu + C = 0 definirano kao:

Dokaz. Pusti poentu M 1 (x 1, y 1)- osnova okomice ispuštena iz tačke M za dato

direktno. Zatim udaljenost između tačaka M I M 1:

(1)

Koordinate x 1 I u 1 može se naći kao rješenje sistema jednačina:

Druga jednačina sistema je jednačina prave koja prolazi kroz datu tačku M 0 okomito

data prava linija. Ako transformišemo prvu jednačinu sistema u oblik:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

tada, rješavanjem, dobijamo:

Zamjenom ovih izraza u jednačinu (1) nalazimo:

Teorema je dokazana.

Da bi se jedna ravan povukla kroz bilo koje tri tačke u prostoru, potrebno je da te tačke ne leže na istoj pravoj liniji.

Razmotrimo tačke M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) u opštem Dekartovom koordinatnom sistemu.

Da bi proizvoljna tačka M(x, y, z) ležala u istoj ravni sa tačkama M 1, M 2, M 3, potrebno je da vektori budu komplanarni.

(
) = 0

dakle,

Jednačina ravni koja prolazi kroz tri tačke:

Jednačina ravni date dvije tačke i vektor kolinearan ravni.

Neka su date tačke M 1 (x 1,y 1,z 1),M 2 (x 2,y 2,z 2) i vektor
.

Napravimo jednačinu za ravan koja prolazi kroz date tačke M 1 i M 2 i proizvoljnu tačku M (x, y, z) paralelnu vektoru .

Vektori
i vektor
mora biti komplanaran, tj.

(
) = 0

Jednačina ravni:

Jednadžba ravni koristeći jednu tačku i dva vektora,

kolinearno ravni.

Neka su data dva vektora
I
, kolinearne ravni. Zatim za proizvoljnu tačku M(x, y, z) koja pripada ravni, vektori
mora biti komplanaran.

Jednačina ravni:

Jednadžba ravni po tački i vektor normale .

Teorema. Ako je tačka M data u prostoru 0 (X 0 , y 0 , z 0 ), zatim jednačina ravnine koja prolazi kroz tačku M 0 okomito na vektor normale (A, B, C) ima oblik:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Dokaz. Za proizvoljnu tačku M(x, y, z) koja pripada ravni, sastavljamo vektor. Jer vektor je normalni vektor, onda je okomit na ravan i, prema tome, okomit na vektor
. Zatim skalarni proizvod

= 0

Tako dobijamo jednačinu ravni

Teorema je dokazana.

Jednačina ravnine u segmentima.

Ako u opštoj jednadžbi Ax + Bi + Cz + D = 0 obje strane podijelimo sa (-D)

,

zamjena
, dobijamo jednadžbu ravnine u segmentima:

Brojevi a, b, c su tačke preseka ravni sa x, y, z osa, respektivno.

Jednadžba ravnine u vektorskom obliku.

Gdje

- radijus vektor trenutne tačke M(x, y, z),

Jedinični vektor koji ima smjer okomice spuštene na ravan od početka.

,  i  su uglovi formirani ovim vektorom sa osama x, y, z.

p je dužina ove okomice.

U koordinatama ova jednadžba izgleda ovako:

xcos + ycos + zcos - p = 0.

Udaljenost od tačke do ravni.

Udaljenost od proizvoljne tačke M 0 (x 0, y 0, z 0) do ravni Ax+By+Cz+D=0 je:

Primjer. Naći jednačinu ravni, znajući da je tačka P(4; -3; 12) osnova okomice spuštene iz početka u ovu ravan.

Dakle, A = 4/13; B = -3/13; C = 12/13, koristimo formulu:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Primjer. Naći jednačinu ravni koja prolazi kroz dvije tačke P(2; 0; -1) i

Q(1; -1; 3) okomito na ravan 3x + 2y – z + 5 = 0.

Vektor normale na ravan 3x + 2y – z + 5 = 0
paralelno sa željenom ravninom.

Dobijamo:

Primjer. Naći jednadžbu ravnine koja prolazi kroz tačke A(2, -1, 4) i

B(3, 2, -1) okomito na ravan X + at + 2z – 3 = 0.

Tražena jednačina ravni ima oblik: A x+B y+C z+ D = 0, vektor normale na ovu ravan (A, B, C). Vector
(1, 3, -5) pripada ravni. Ravan koja nam je data, okomita na željenu, ima normalan vektor (1, 1, 2). Jer tačke A i B pripadaju obema ravnima, pa su ravni međusobno okomite, dakle

Dakle, normalni vektor (11, -7, -2). Jer tačka A pripada željenoj ravni, tada njene koordinate moraju zadovoljiti jednačinu ove ravni, tj. 112 + 71 - 24 +D= 0;D= -21.

Ukupno dobijamo jednačinu ravni: 11 x - 7y – 2z – 21 = 0.

Primjer. Naći jednačinu ravni, znajući da je tačka P(4, -3, 12) osnova okomice spuštene iz početka u ovu ravan.

Pronalaženje koordinata vektora normale
= (4, -3, 12). Tražena jednačina ravni ima oblik: 4 x – 3y + 12z+ D = 0. Da bismo pronašli koeficijent D, zamjenjujemo koordinate tačke P u jednačinu:

16 + 9 + 144 + D = 0

Ukupno dobijamo traženu jednačinu: 4 x – 3y + 12z – 169 = 0

Primjer. Date su koordinate vrhova piramide A 1 (1; 0; 3), A 2 (2; -1; 3), A 3 (2; 1; 1),

    Odredite dužinu ivice A 1 A 2.

    Pronađite ugao između ivica A 1 A 2 i A 1 A 4.

    Pronađite ugao između ivice A 1 A 4 i lica A 1 A 2 A 3.

Prvo nađemo vektor normale na lice A 1 A 2 A 3 kao unakrsni proizvod vektora
I
.

= (2-1; 1-0; 1-3) = (1; 1; -2);

Nađimo ugao između vektora normale i vektora
.

-4 – 4 = -8.

Željeni ugao  između vektora i ravni će biti jednak  = 90 0 - .

    Pronađite površinu lica A 1 A 2 A 3.

    Pronađite zapreminu piramide.

    Nađite jednačinu ravnine A 1 A 2 A 3.

Koristimo formulu za jednadžbu ravni koja prolazi kroz tri tačke.

2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0;

Kada koristite kompjutersku verziju “ Viši kurs matematike” možete pokrenuti program koji će riješiti gornji primjer za bilo koje koordinate vrhova piramide.

Da biste pokrenuli program, dvaput kliknite na ikonu:

U prozoru programa koji se otvori unesite koordinate vrhova piramide i pritisnite Enter. Na ovaj način, sve bodove odluke mogu se dobiti jedna po jedna.

Napomena: Da biste pokrenuli program, program Maple ( Waterloo Maple Inc.) bilo koje verzije, počevši od MapleV izdanja 4, mora biti instaliran na vašem računaru.