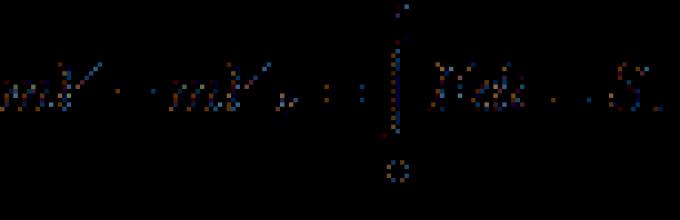(Fragmenti matematičke simfonije)

Veza između impulsa sile i osnovne jednadžbe Njutnove dinamike izražena je teoremom o promjeni impulsa materijalne tačke.

Teorema. Promjena količine gibanja materijalne tačke u određenom vremenskom periodu jednaka je impulsu sile () koja djeluje na materijalna tačka u istom vremenskom periodu. Matematički dokaz ove teoreme može se nazvati fragmentom matematičke simfonije. Evo ga.

Diferencijalni impuls materijalne tačke jednak je elementarnom impulsu sile koja djeluje na materijalnu tačku. Integrirajući izraz (128) za diferencijalni impuls materijalne tačke imamo

(129)

Teorema je dokazana i matematičari smatraju svoju misiju završenom, ali inženjeri, čija je sudbina sveto veruju u matematičare, imaju pitanja kada koriste dokazanu jednačinu (129). Ali oni su čvrsto blokirani redoslijedom i ljepotom matematičkih operacija (128 i 129), koje nas fasciniraju i ohrabruju da ih nazovemo fragmentom matematičke simfonije. Koliko se generacija inženjera slagalo s matematičarima i divilo se misteriji njihovih matematičkih simbola! Ali onda se pojavio inženjer koji se nije složio sa matematičarima i postavljao im pitanja.

Dragi matematičari! Zašto nijedan vaš udžbenik iz teorijske mehanike ne govori o procesu primjene vašeg simfonijskog rezultata (129) u praksi, na primjer, kada opisujete proces ubrzanja automobila? Lijeva strana jednačine (129) je vrlo jasna. Automobil počinje ubrzanje od brzine i završava ga, na primjer, pri brzini. Sasvim je prirodno da jednačina (129) postaje

I odmah se nameće prvo pitanje: kako možemo iz jednačine (130) odrediti silu pod čijim se uticajem automobil ubrzava do brzine od 10 m/s? Odgovor na ovo pitanje ne nalazi se ni u jednom od bezbrojnih udžbenika teorijske mehanike. Idemo dalje. Nakon ubrzanja, automobil se počinje ravnomjerno kretati brzinom od 10 m/s. Koja sila pokreće auto?????????? Nemam izbora nego da pocrvenim zajedno sa matematičarima. Prvi zakon Newtonove dinamike kaže da kada se automobil kreće ravnomjerno, na njega ne djeluju sile, a automobil, figurativno rečeno, kihne na ovaj zakon, troši benzin i radi, krećući se, na primjer, na udaljenosti od 100 km. Gdje je sila koja je izvršila rad da pomjeri automobil 100 km? Simfonijska matematička jednačina (130) šuti, ali život ide dalje i traži odgovor. Počinjemo da ga tražimo.

Pošto se automobil kreće pravolinijski i jednoliko, sila koja ga kreće je konstantna po veličini i smjeru i jednačina (130) postaje

(131)

Dakle, jednačina (131) u ovom slučaju opisuje ubrzano kretanje tijela. Čemu je jednaka sila? Kako izraziti njegovu promjenu tokom vremena? Matematičari radije zaobilaze ovo pitanje i prepuštaju ga inženjerima, smatrajući da moraju tražiti odgovor na ovo pitanje. Inženjerima preostaje jedna opcija - da uzmu u obzir da ako nakon završetka ubrzanog kretanja tijela, počne faza ujednačenog kretanja, koja je popraćena akcijom konstantna sila sadašnja jednačina (131) za trenutak prijelaza iz ubrzanog u ravnomjerno kretanje u ovom obliku

(132)

Strelica u ovoj jednačini ne znači rezultat integracije ove jednačine, već proces prelaska iz njenog integralnog oblika u pojednostavljeni oblik. Sila u ovoj jednačini je ekvivalentna prosječnoj sili koja je promijenila impuls tijela od nule do konačne vrijednosti. Dakle, dragi matematičari i teoretičari fizičari, nepostojanje vaše metode za određivanje veličine vašeg impulsa tjera nas da pojednostavimo postupak određivanja sile, a odsustvo metode za određivanje vremena djelovanja ove sile nas generalno stavlja u beznadežan položaj i primorani smo da koristimo izraz za analizu procesa promjene impulsa tijela. Rezultat je da što duže sila djeluje, to je veći njen impuls. Ovo je jasno u suprotnosti s dugo uspostavljenom idejom da što je kraće trajanje njenog djelovanja, to je veći impuls sile.

Obratimo pažnju na činjenicu da se promjena momenta gibanja materijalne tačke (impulsa sile) tokom njenog ubrzanog kretanja događa pod djelovanjem Newtonove sile i sila otpora kretanju, u obliku sila koje stvaraju mehanički otpori i sila inercije. Ali Njutnova dinamika u velikoj većini problema zanemaruje silu inercije, a mehanodinamika navodi da se promena momenta kretanja tela tokom njegovog ubrzanog kretanja dešava zbog viška Njutnove sile nad silama otpora kretanju, uključujući sila inercije.

Kada se tijelo kreće usporeno, na primjer, automobil s isključenim zupčanikom, nema Newtonove sile, a promjena količine kretanja automobila nastaje zbog viška sila otpora kretanju nad silom inercija, koja pokreće automobil kada se kreće polako.

Kako sada možemo vratiti rezultate zapaženih „simfonijskih” matematičkih radnji (128) u glavni tok uzročno-posledičnih veza? Postoji samo jedan izlaz - pronaći novu definiciju pojmova "impuls sile" i "udarna sila". Da biste to učinili, podijelite obje strane jednačine (132) s vremenom t. Kao rezultat ćemo imati

. (133)

Zapazimo da je izraz mV/t brzina promjene momenta (mV/t) materijalne tačke ili tijela. Ako uzmemo u obzir da je V/t ubrzanje, onda je mV/t sila koja mijenja impuls tijela. Ista dimenzija lijevo i desno od znaka jednakosti daje nam za pravo da silu F nazovemo udarnom silom i označimo je simbolom, a impuls S udarnim impulsom i označimo je simbolom. Ovo dovodi do nove definicije udarne sile. Udarna sila koja djeluje na materijalnu tačku ili tijelo jednaka je omjeru promjene količine gibanja materijalne tačke ili tijela i vremena ove promjene.

Obratimo posebnu pažnju na činjenicu da u formiranju udarnog impulsa (134) učestvuje samo Njutnova sila, koja je promenila brzinu automobila od nula vrijednost do maksimuma - , stoga jednadžba (134) u potpunosti pripada Njutnovoj dinamici. Budući da je mnogo lakše eksperimentalno odrediti veličinu brzine nego odrediti ubrzanje, formula (134) je vrlo zgodna za proračune.

Ovaj neobičan rezultat slijedi iz jednačine (134).

Obratimo pažnju na činjenicu da je prema novim zakonima mehanodinamike generator impulsa sile pri ubrzanom kretanju materijalne tačke ili tijela Newtonova sila. Formira ubrzanje kretanja tačke ili tijela, pri čemu automatski nastaje inercijska sila, usmjerena suprotno od Newtonove sile i udarna Njutnova sila mora nadvladati djelovanje inercijalne sile, stoga inercijska sila mora biti predstavljena u ravnoteža sila na lijevoj strani jednačine (134). Pošto je inercijska sila jednaka masi tačke ili tijela pomnoženoj sa usporavanjem koje ono formira, tada jednačina (134) postaje

(136)

Dragi matematičari! Pogledajte u kakvom je obliku matematički model, koji opisuje udarni impuls, koji ubrzava kretanje pogođenog tijela od nulte brzine do maksimalne V (11). Sada provjerimo njegov rad u određivanju udarnog impulsa, koji je jednak sili udarca koja je ispalila 2. pogonski agregat SShG-a (Sl. 120), a mi ćemo vam ostaviti vašu beskorisnu jednačinu (132). Kako ne bismo komplicirali prezentaciju, za sada ćemo ostaviti formulu (134) na miru i koristiti formule koje daju prosječne vrijednosti sila. Vidite u koju poziciju stavljate inženjera koji pokušava riješiti određeni problem.

Počnimo s Newtonovom dinamikom. Stručnjaci su utvrdili da se 2. agregat popeo na visinu od 14 m. Pošto se uzdigao u polju gravitacije, onda je na visini od h=14m on potencijalna energija ispostavilo se da su jednaki

a prosječna kinetička energija bila je jednaka

Rice. 120. Fotografija turbinske prostorije prije katastrofe

Iz jednakosti kinetičke (138) i potencijalne (137) energije slijedi prosječna brzina porasta agregata (sl. 121, 122)

Rice. 121. Foton turbinske sobe nakon katastrofe

Prema novim zakonima mehanodinamike, uspon agregata se sastojao od dvije faze (slika 123): prva faza OA - ubrzani uspon i druga faza AB - spori porast , , .

Vrijeme i udaljenost njihovog djelovanja su približno jednaki (). Tada će se kinematička jednačina ubrzane faze podizanja agregata napisati na sljedeći način:

. (140)

Rice. 122. Pogled na bunar agregata i sam agregat nakon havarije

Zakon promjene brzine porasta agregata u prvoj fazi ima oblik

. (141)

Rice. 123. Pravilnost promjena brzine leta V pogonske jedinice

Zamjenom vremena iz jednačine (140) u jednačinu (141), imamo

. (142)

Vrijeme podizanja bloka u prvoj fazi određuje se iz formule (140)

. (143)

Tada će ukupno vrijeme podizanja pogonske jedinice na visinu od 14 m biti jednako . Masa agregata i poklopca je 2580 tona. Prema Newtonovskoj dinamici, sila koja je podigla agregat jednaka je

Dragi matematičari! Pratimo vaše simfonijske matematičke rezultate i zapisujemo vašu formulu (129), slijedeći Newtonovu dinamiku, da odredimo udarni impuls koji je pokrenuo 2. pogonsku jedinicu

i postaviti osnovno pitanje: kako odrediti trajanje udarnog impulsa koji je ispalio 2. agregat????????????

Dragi!!! Sjetite se koliko su kredom ispisivale generacije vaših kolega na tablama, mukotrpno učeći studente kako da odrede udarni impuls, a niko nije objasnio kako odrediti trajanje udarnog impulsa u svakom konkretnom slučaju. Reći ćete da je trajanje udarnog impulsa jednako vremenskom intervalu promjene brzine pogonske jedinice od nule do, pretpostavićemo, maksimalne vrijednosti od 16,75 m/s (139). Nalazi se u formuli (143) i jednak je 0,84 s. Za sada se slažemo s vama i određujemo prosječnu vrijednost udarnog impulsa

Odmah se postavlja pitanje: zašto je veličina udarnog impulsa (146) manja od Njutnove sile od 50600 tona? Vi, dragi matematičari, nemate odgovor. Idemo dalje.

Prema Newtonovoj dinamici, glavna snaga, koja je odoljela porastu agregata, je sila gravitacije. Budući da je ova sila usmjerena protiv kretanja pogonske jedinice, ona stvara usporavanje, koje je jednako ubrzanju slobodan pad. Tada je gravitaciona sila koja djeluje na agregat koji leti prema gore jednaka

Njutnova dinamika ne uzima u obzir druge sile koje su onemogućavale dejstvo Njutnove sile od 50.600 tona (144), a mehanodinamika navodi da se podizanju agregata odupirala i inercijalna sila jednaka

Odmah se postavlja pitanje: kako pronaći količinu usporavanja u kretanju agregata? Njutnova dinamika šuti, ali mehanodinamika odgovara: u trenutku dejstva Njutnove sile, koja je podigla agregat, odupirali su joj se: sila gravitacije i sila inercije, dakle jednačina sila koje deluju na snagu jedinica u tom trenutku piše se na sljedeći način.

Mjera kvantiteta pokreta mehaničko kretanje, ako mehaničko kretanje pređe u mehaničko. Na primjer, mehaničko kretanje loptice za bilijar (slika 22) prije udara pretvara se u mehaničko kretanje lopti nakon udara. Za tačku, impuls je jednak proizvodu .

Mjera sile u ovom slučaju je impuls sile

. (9.1)

Zamah određuje djelovanje sile tokom određenog vremenskog perioda . Za materijalnu tačku, teorema o promjeni impulsa može se koristiti u diferencijalnom obliku
(9.2) ili integralni (konačan) oblik
. (9.3)

Promjena količine gibanja materijalne tačke u određenom vremenskom periodu jednaka je impulsu svih sila koje se primjenjuju na tačku u istom vremenu.

Slika 22

Prilikom rješavanja zadataka teorema (9.3) se češće koristi u projekcijama na koordinatne ose
;

; (9.4)

.

Koristeći teoremu o promjeni količine gibanja tačke moguće je riješiti probleme u kojima na tačku ili tijelo koje se translatorno kreće djeluju konstantne ili promjenjive sile koje zavise od vremena, a date i tražene veličine uključuju vrijeme kretanje i brzine na početku i na kraju kretanja. Zadaci korištenjem teoreme rješavaju se sljedećim redoslijedom:

1. izabrati koordinatni sistem;

2. prikazati sve date (aktivne) sile i reakcije koje djeluju na tačku;

3. zapisati teoremu o promjeni količine gibanja tačke u projekcijama na odabrane koordinatne ose;

4. odrediti potrebne količine.

PRIMJER 12.

Čekić težine G=2t pada sa visine h=1m na radni predmet za vrijeme t=0.01s i štanca dio (sl. 23). Odredite prosječnu silu pritiska čekića na radni predmet.

RJEŠENJE.

1. Radni predmet je podložan sili gravitacije čekića i reakcija tla . Veličina reakcije podrške se mijenja tokom vremena, pa razmotrimo njenu prosječnu vrijednost
.

2. usmjeriti koordinatnu os y okomito prema dolje i primijeniti teoremu o promjeni količine gibanja tačke u projekciji na ovu os:
, (1) gdje -- brzina čekića na kraju udarca;

-- početna brzina čekića u trenutku kontakta sa obratkom.

3. Odrediti brzinu pomirimo se diferencijalna jednadžba kretanje čekića u projekciji na y-os:

. (2)

Odvojimo varijable i dvaput integrišemo jednačinu (2):
;

;

. Konstante integracije C 1, C 2 nalazimo iz početnih uslova. Pri t=0 V y =0, tada je C 1 =0; y=0, tada je C 2 =0. Dakle, čekić se kreće u skladu sa zakonom
, (3) i brzina čekića se mijenja u skladu sa zakonom
. (4) Izrazimo vrijeme kretanja čekića iz (3) i zamijenimo ga u (4)
;
. (5)

4. Projekciju impulsa vanjskih sila nalazimo na y-osu koristeći formulu:
. (6) Zamijenite (5) i (6) u (1):
, odakle nalazimo reakciju oslonca, a samim tim i željeni pritisak čekića na radni predmet
T.

Slika 24

 TO

gdje je M masa sistema, V c je brzina centar mase. Teorema o promjeni impulsa mehaničkog sistema može se napisati u diferencijalnom i konačnom (integralnom) obliku:
;

. (9.7)

 Količina kretanja mehaničkog sistema može se definirati kao zbir količina kretanja tačaka sistema
. (9.5) Moment kretanja sistema ili krutog tijela može se odrediti poznavanjem mase sistema i brzine centra mase
, (9.6)

Promjena količine gibanja mehaničkog sistema u određenom vremenskom periodu jednaka je zbiru impulsa vanjskih sila koje djeluju za isto vrijeme. Ponekad je zgodnije koristiti teoremu o promjeni impulsa u projekciji na koordinatne ose
; (9.8)
. (9.9)

Zakon održanja količine kretanja kaže da u odsustvu vanjskih sila, impuls mehaničkog sistema ostaje konstantan. Akcija unutrašnje sile ne može promijeniti zamah sistema. Iz jednačine (9.6) jasno je da kada
,
.

Ako
, To
ili
.

D

propeler ili propeler, mlazni pogon. Lignje se kreću u trzajima, izbacujući vodu iz mišićne vreće poput vodenog topa (Sl. 25). Odbijena voda ima određenu količinu kretanja usmjerenu unazad. Lignja dobija odgovarajuću brzinu kretanje naprijed zbog reaktivne vučne sile , jer prije nego lignja iskoči sila izbalansiran gravitacijom .

Učinak zakona održanja količine gibanja mehaničkog sistema može se ilustrovati na primjeru fenomena trzaja ili prevrtanja pri pucanju, radu

Primjena teoreme o promjeni impulsa omogućava nam da isključimo sve unutrašnje sile iz razmatranja.

PRIMJER 13.

Vitlo A sa bubnjem poluprečnika r postavlja se na železničku platformu koja slobodno stoji na tračnicama (sl. 26). Vitlo je dizajnirano za pomicanje tereta B mase m 1 duž platforme. Težina platforme sa vitlom m 2. Bubanj vitla se okreće u skladu sa zakonom
. U početnom trenutku sistem je bio mobilan. Zanemarujući trenje, pronađite zakon promjene brzine platforme nakon uključivanja vitla.

R RJEŠENJE.

1. Razmotrite platformu, vitlo i teret kao jedinstveni mehanički sistem koji je podložan spoljne sile: gravitacija opterećenja i platforme i reakcije I
.

2. Kako su sve vanjske sile okomite na osu x, tj.
, primjenjujemo zakon održanja impulsa mehaničkog sistema u projekciji na x-osu:
. U početnom trenutku sistem je bio nepomičan, dakle,

Izrazimo količinu kretanja sistema u proizvoljnom trenutku. Platforma se kreće naprijed velikom brzinom , teret prolazi kroz složeno kretanje koje se sastoji od relativnog kretanja duž platforme brzinom i prijenosno kretanje zajedno s platformom pri brzini ., gdje
. Platforma će se kretati u smjeru suprotnom od relativnog kretanja tereta.

PRIMJER 14.

M

RJEŠENJE.

1. Primijenimo teoremu o promjeni impulsa mehaničkog sistema u projekciji na x-osu. Pošto su sve vanjske sile koje djeluju na sistem vertikalne, onda
, Onda
, gdje
. (1)

2. Izrazimo projekciju momenta na x-osu za mehanički sistem koji se razmatra
,

 Mehanički sistem se sastoji od pravokutne vertikalne ploče 1 mase m 1 = 18 kg, koja se kreće duž horizontalnih vodilica i tereta D mase m 2 = 6 kg. U trenutku t 0 =0, kada se ploča kretala brzinom u 0 =2m/s, teret je počeo da se kreće duž rova ​​u skladu sa jednačinom S=AD=0,4sin( t 2) (S-u metrima, t-u sekundama), (Sl. 26). Odrediti brzinu ploče u trenutku t 1 = 1s, koristeći teoremu o promjeni količine gibanja mehaničkog sistema.

Gdje ,
-- količina kretanja ploče i opterećenja, respektivno.


;
, Gdje --apsolutna brzina tereta D. Iz jednakosti (1) slijedi da je K 1x + K 2x =C 1 ili m 1 u x +m 2 V Dx =C 1. (2) Da biste odredili V Dx, smatrajte kretanje tereta D kompleksnim, uzimajući u obzir njegovo kretanje u odnosu na ploču relativno, a kretanje same ploče prenosivim, tada
, (3)
;ili u projekciji na x osu: . (4) Zamijenimo (4) u (2):
. (5) Integracionu konstantu C 1 određujemo iz početnih uslova: pri t=0 u=u 0 ; (m 1 +m 2)u 0 =C 1. (6) Zamjenom vrijednosti konstante C 1 u jednačinu (5) dobijamo

gospođa.

Za materijalnu tačku, osnovni zakon dinamike može se predstaviti kao

Množenjem obe strane ove relacije na levoj strani vektorski radijus vektorom (slika 3.9) dobijamo

(3.32)

Na desnoj strani ove formule imamo moment sile u odnosu na tačku O. Lijevu stranu transformiramo primjenom formule za izvod vektorskog proizvoda

Ali Kako vektorski proizvod paralelni vektori. Nakon ovoga dobijamo

(3.33)

Prvi izvod u odnosu na vrijeme momenta momenta momenta tačke u odnosu na bilo koje središte jednak je momentu sile u odnosu na isto središte.


Primjer izračunavanja ugaonog momenta sistema. Izračunajte kinetički moment u odnosu na tačku O sistema koji se sastoji od cilindrične osovine mase M = 20 kg i polumjera R = 0,5 m i silaznoga opterećenja mase m = 60 kg (slika 3.12). Osovina rotira oko ose Oz sa ugaonom brzinom ω = 10 s -1.

Slika 3.12

; ;

Za date ulazne podatke, ugaoni moment sistema

Teorema o promjeni ugaonog momenta sistema. Rezultirajuće vanjske i unutrašnje sile primjenjujemo na svaku tačku sistema. Za svaku tačku sistema možete primijeniti teoremu o promjeni ugaonog momenta, na primjer u obliku (3.33)

Zbrajanjem svih tačaka sistema i uzimajući u obzir da je zbir izvoda jednak derivatu zbira, dobijamo

Određivanjem kinetičkog momenta sistema i svojstava spoljašnjih i unutrašnjih sila

Stoga se rezultujući odnos može predstaviti kao

Prvi vremenski izvod ugaonog momenta sistema u odnosu na bilo koju tačku jednak je glavnom momentu spoljnih sila koje deluju na sistem u odnosu na istu tačku.

3.3.5. Rad sile

1) Elementarni rad sile jednak je skalarnom proizvodu sile i diferencijalnog radijusa vektora tačke primjene sile (slika 3.13)

Slika 3.13

Izraz (3.36) se također može napisati u sljedećim ekvivalentnim oblicima

gdje je projekcija sile na smjer brzine tačke primjene sile.

2) Rad sile na konačnom pomjeranju

Integracijom elementarnog rada sile dobijamo sljedeće izraze za rad sile na konačnom pomaku od tačke A do tačke B

3) Rad konstantne sile

Ako je sila konstantna, onda iz (3.38) slijedi

Rad konstantne sile ne zavisi od oblika putanje, već zavisi samo od vektora pomaka tačke primene sile.

4) Rad sile težine

Za silu težine (slika 3.14) i iz (3.39) dobijamo

Slika 3.14

Ako se kretanje odvija od tačke B do tačke A, onda

Uglavnom

Znak “+” odgovara kretanju nadole tačke primene sile, znak “-” – prema gore.

4) Rad elastične sile

Neka je os opruge usmerena duž x ose (slika 3.15), a kraj opruge se pomera od tačke 1 do tačke 2, tada iz (3.38) dobijamo

Ako je krutost opruge With, pa onda

A (3.41)

Ako se kraj opruge pomakne od točke 0 do točke 1, tada u ovom izrazu zamjenjujemo , , tada će rad elastične sile poprimiti oblik

(3.42)

gdje je izduženje opruge.

Slika 3.15

5) Rad sile primijenjen na tijelo koje se rotira. Djelo trenutka.

Na sl. Slika 3.16 prikazuje rotirajuće tijelo na koje se primjenjuje proizvoljna sila. Tokom rotacije, tačka primjene ove sile se kreće kružno.

Neka se materijalna tačka kreće pod uticajem sile F. Potrebno je odrediti kretanje ove tačke u odnosu na pokretni sistem Oxyz(vidi složeno kretanje materijalne tačke), koja se kreće na poznati način u odnosu na stacionarni sistem O 1 x 1 y 1 z 1 .

Osnovna jednadžba dinamike u stacionarnom sistemu

Zapišimo apsolutno ubrzanje tačke koristeći Coriolisovu teoremu

Gdje a abs– apsolutno ubrzanje;

a rel– relativno ubrzanje;

a lane– prijenosno ubrzanje;

a jezgro– Coriolisovo ubrzanje.

Prepišimo (25) uzimajući u obzir (26)

Hajde da uvedemo notaciju
- prenosiva sila inercije,
- Coriolisova inercijska sila. Tada jednačina (27) poprima oblik

Osnovna jednadžba dinamike za proučavanje relativnog kretanja (28) napisana je na isti način kao i za apsolutno kretanje, samo se silama koje djeluju na tačku moraju dodati prijenosne i Coriolisove sile inercije.

Opće teoreme o dinamici materijalne tačke

Prilikom rješavanja mnogih zadataka možete koristiti unaprijed napravljene blanke dobivene na osnovu Newtonovog drugog zakona. Takve metode rješavanja problema su objedinjene u ovom odeljku.

Teorema o promjeni impulsa materijalne tačke

Predstavimo sljedeće dinamičke karakteristike:

1. Zamah materijalne tačke – vektorska količina, jednak proizvodu mase tačke i njenog vektora brzine


. (29)

2. Impuls sile

Elementarni impuls sile– vektorska količina jednaka proizvodu vektora sile i elementarnog vremenskog intervala


(30).

Onda puni impuls

. (31)

At F=const dobijamo S=Ft.

Ukupni impuls za konačan vremenski period može se izračunati samo u dva slučaja, kada je sila koja djeluje na tačku konstantna ili ovisi o vremenu. U drugim slučajevima, potrebno je izraziti silu kao funkciju vremena.

Jednakost dimenzija impulsa (29) i impulsa (30) omogućava nam da uspostavimo kvantitativan odnos između njih.

Razmotrimo kretanje materijalne tačke M pod dejstvom proizvoljne sile F duž proizvoljne putanje.

O UD:
. (32)

Odvajamo varijable u (32) i integrišemo

. (33)

Kao rezultat, uzimajući u obzir (31), dobijamo

. (34)

Jednačina (34) izražava sljedeću teoremu.

Teorema: Promjena količine gibanja materijalne tačke u određenom vremenskom periodu jednaka je impulsu sile koja djeluje na tačku u istom vremenskom intervalu.

Prilikom rješavanja zadataka jednačina (34) se mora projicirati na koordinatne ose

Ovu teoremu je pogodno koristiti kada se među datim i nepoznatim veličinama nalaze masa tačke, njena početna i konačna brzina, sile i vrijeme kretanja.

Teorema o promjeni ugaonog momenta materijalne tačke

M
moment impulsa materijalne tačke u odnosu na centar jednak je proizvodu modula impulsa tačke i ramena, tj. najkraća udaljenost (okomita) od centra do linije koja se poklapa sa vektor brzine

, (36)

. (37)

Odnos između momenta sile (uzroka) i momenta impulsa (posledice) utvrđuje se sljedećom teoremom.

Neka je tačka M date mase m kreće se pod uticajem sile F.

,
,

, (38)

. (39)

Izračunajmo derivaciju (39)

. (40)

Kombinujući (40) i (38), konačno dobijamo

. (41)

Jednačina (41) izražava sljedeću teoremu.

Teorema: Vremenski izvod vektora ugaonog momenta materijalne tačke u odnosu na neki centar jednak je momentu sile koja deluje na tačku u odnosu na isto središte.

Prilikom rješavanja zadataka jednačina (41) se mora projicirati na koordinatne ose

U jednadžbi (42) momenti momenta momenta i sile se računaju u odnosu na koordinatne ose.

Iz (41) slijedi zakon održanja ugaonog momenta (Keplerov zakon).

Ako je moment sile koja djeluje na materijalnu tačku u odnosu na bilo koji centar jednak nuli, tada ugaoni moment tačke u odnosu na ovo središte zadržava svoju veličinu i smjer.

Ako
, To
.

Teorema i zakon održanja koriste se u problemima koji uključuju krivolinijsko kretanje, posebno pod dejstvom centralnih snaga.

Količina kretanja sistema, kao vektorska veličina, određena je formulama (4.12) i (4.13).

Teorema. Izvod impulsa sistema u odnosu na vrijeme jednak je geometrijskom zbiru svih vanjskih sila koje djeluju na njega.

U projekcijama kartezijanskih osa dobijamo skalarne jednadžbe.

Možete napisati vektor

(4.28)

i skalarne jednačine

Koji izražavaju teoremu o promjeni količine gibanja sistema u integralnom obliku: promjena impulsa sistema u određenom vremenskom periodu jednaka je zbiru impulsa u istom vremenskom periodu. Prilikom rješavanja zadataka češće se koriste jednačine (4.27).

Zakon održanja impulsa

Teorema o promjeni ugaonog momenta

Teorema o promjeni ugaonog momenta tačke u odnosu na centar: vremenski izvod ugaonog momenta tačke u odnosu na fiksni centar jednak je vektorskom momentu sile koja djeluje na tačku u odnosu na isti centar.

Or (4.30)

Upoređujući (4.23) i (4.30), vidimo da su momenti vektora i povezani istom zavisnošću kao što su vektori i sami povezani (slika 4.1). Ako projektiramo jednakost na osu koja prolazi kroz centar O, dobićemo

(4.31)

Ova jednakost izražava teoremu o ugaonom momentu tačke u odnosu na osu.

Rice. 4.1.
Teorema o promjeni glavnog ugaonog momenta ili ugaonog momenta mehaničkog sistema u odnosu na centar: vremenski derivat kinetičkog ugaonog momenta sistema u odnosu na neko fiksno središte jednak je zbiru momenata svih vanjskih sila u odnosu na isti centar.

(4.32)

Ako projiciramo izraz (4.32) na osu koja prolazi kroz centar O, dobićemo jednakost koja karakteriše teoremu o promeni ugaonog momenta u odnosu na osu.

(4.33)

Zamjenom (4.10) u jednakost (4.33), možemo napisati diferencijalnu jednačinu rotirajućeg krutog tijela (točkovi, osovine, osovine, rotori, itd.) u tri oblika.

(4.34)

(4.35)

(4.36)

Stoga je preporučljivo koristiti teoremu o promjeni kinetičkog momenta za proučavanje kretanja krutog tijela, što je vrlo uobičajeno u tehnici, njegova rotacija oko fiksne ose.

Zakon održanja ugaonog momenta sistema

1. Neka u izrazu (4.32) .

Tada iz jednačine (4.32) slijedi da, tj. ako je zbir momenata svih vanjskih sila primijenjenih na sistem u odnosu na dati centar jednak nuli, tada će kinetički moment sistema u odnosu na ovaj centar biti numerički i usmjereno konstantan.

2. Ako , onda . Dakle, ako je zbroj momenata vanjskih sila koje djeluju na sistem u odnosu na određenu osu jednak nuli, tada će kinetički moment sistema u odnosu na ovu osu biti konstantna vrijednost.

Ovi rezultati izražavaju zakon održanja ugaonog momenta.

U slučaju rotirajućeg krutog tijela, iz jednakosti (4.34) slijedi da, ako je , onda . Odavde dolazimo do sljedećih zaključaka:

Ako je sistem nepromjenjiv (apsolutno solidan), dakle, i kruto tijelo rotira oko fiksne ose sa konstantnom ugaonom brzinom.

Ako je sistem promjenjiv, onda . Sa povećanjem (tada se pojedini elementi sistema udaljavaju od ose rotacije), ugaona brzina se smanjuje, jer , a pri opadanju se povećava, tako da je u slučaju promjenljivog sistema uz pomoć unutrašnjih sila moguće mijenjati ugaonu brzinu.

Drugi zadatak D2 testni rad je posvećena teoremi o promjeni ugaonog momenta sistema u odnosu na osu.

Problem D2

Homogena horizontalna platforma (kružna poluprečnika R ili pravougaona sa stranicama R i 2R, gde je R = 1,2 m) mase kg rotira ugaonom brzinom oko vertikalne ose z, udaljene od centra mase C platforme na a rastojanje OC = b (sl. E2.0 – D2.9, tabela D2); Dimenzije za sve pravougaone platforme prikazane su na Sl. D2.0a (pogled odozgo).

U trenutku, teret D mase kg počinje da se kreće duž platforme (pod uticajem unutrašnjih sila) prema zakonu, gde se s izražava u metrima, t - u sekundama. Istovremeno, par sila sa momentom M (naveden u njutonometrima; na M< 0 его направление противоположно показанному на рисунках).

Odrediti, zanemarujući masu osovine, zavisnost tj. ugaona brzina platforme kao funkcija vremena.

Na svim slikama, opterećenje D je prikazano u poziciji u kojoj je s > 0 (kada je s< 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на datoj udaljenosti OC = b iz centra C.

Upute. Zadatak D2 – primijeniti teoremu o promjeni ugaonog momenta sistema. Kada se teorema primjenjuje na sistem koji se sastoji od platforme i tereta, ugaoni moment sistema u odnosu na osu z određuje se kao zbir momenata platforme i opterećenja. Treba uzeti u obzir da je apsolutna brzina tereta zbir relativne i prenosive brzine, tj. . Dakle, količina kretanja ovog tereta . Tada možete koristiti Varignonovu teoremu (statiku), prema kojoj ; ovi momenti se računaju na isti način kao i momenti sila. Rješenje je detaljnije objašnjeno u primjeru D2.

Prilikom rješavanja problema korisno je na pomoćnom crtežu prikazati pogled na platformu odozgo (sa z kraja), kao što je to učinjeno na sl. D2.0, a – D2.9, a.

Moment inercije ploče mase m u odnosu na osu Cz, okomitu na ploču i koja prolazi kroz njeno središte mase, jednak je: za pravokutnu ploču sa stranicama i

;

Za okruglu ploču poluprečnika R


Broj uslova b s = F(t) M
R R/2 R R/2 R R/2 R R/2 R R/2 -0,4 0,6 0,8 10 t 0,4 -0,5t -0,6t 0,8t 0,4 0,5 4t -6 -8t -9 6 -10 12

Rice. D2.0
Rice. D2.0a

Rice. D2.1
Rice. D2.1a

Rice. D2.2
Rice. D2.2a

Rice. D2.3
Rice. D2.3a

Rice. D2.4
Rice. D2.4a

Rice. D2.5a
Rice. D2.5

Rice. D2.6
Rice. D2.6a

Rice. D2.7
Rice. D2.7a

Rice. D2.8
Rice. D2.8a

Rice. D2.9
Rice. D2.9a

Rice. D 2

Primjer D2. Homogena horizontalna platforma (pravokutna sa stranicama 2l i l), koja ima masu, kruto je pričvršćena na okomitu osovinu i rotira se s njom oko osi z sa ugaonom brzinom (slika E2a ). U tom trenutku na osovinu počinje djelovati obrtni moment M, usmjeren suprotno ; istovremeno teret D masa koja se nalazi u rovu AB u tački SA, počinje da se kreće duž žlijeba (pod uticajem unutrašnjih sila) po zakonu s = CD = F(t).

Dato: m 1 = 16 kg, t 2= 10 kg, l= 0,5 m, = 2, s = 0,4t 2 (s - u metrima, t - u sekundama), M= kt, Gdje k=6 Nm/s. Definirati: - zakon promjene ugaona brzina platforme.

Rješenje. Zamislite mehanički sistem koji se sastoji od platforme i tereta D. Da bismo odredili w, primjenjujemo teoremu o promjeni ugaonog momenta sistema u odnosu na osu z:

(1)

Opišimo vanjske sile koje djeluju na sistem: gravitacionu silu reakcije i moment M. Pošto su sile i paralelne sa osom z, a reakcije sijeku ovu osu, njihovi momenti u odnosu na osu z jednaki su nula. Zatim, smatrajući da je smjer za trenutak pozitivan (tj. u smjeru suprotnom od kazaljke na satu), dobijamo i jednačina (1) će poprimiti ovaj oblik.