Unija (logički zbir) N događaja naziva se događaj , što se opaža svaki put kada se pojavi barem jedan od događaji . Konkretno, unija događaja A i B naziva se događaj A+ B(neki autori
), što se opaža kada dolaziili A,ili Bili oba ova događaja u isto vreme(Sl. 7). Znak ukrštanja u tekstualnim formulacijama događaja je konjunkcija "ili".

Rice. 7. Kombinovanje A+B događaja

Potrebno je uzeti u obzir da vjerovatnoća događaja P(A) odgovara lijevoj strani osenčenoj na Sl. 7 slike i njen središnji dio, označen kao
. A ishodi koji odgovaraju događaju B nalaze se i na desnoj strani osenčene figure i na označenoj
centralni dio. Dakle, prilikom dodavanja I području
će zapravo biti uključen u ovaj zbir dva puta, a tačan izraz za površinu osenčene figure ima oblik
.

dakle, vjerovatnoća ujedinjenja dva događaja A i B je jednaka

Za veći broj događaja opći računski izraz postaje izuzetno glomazan zbog potrebe da se uzmu u obzir brojne mogućnosti međusobnog preklapanja područja. Međutim, ako su događaji koji se kombinuju nekompatibilni (vidi str. 33), onda je međusobno preklapanje područja nemoguće, a povoljna zona se određuje direktno zbirom površina koje odgovaraju pojedinačnim događajima.

Vjerovatnoća udruženja bilo koji broj nekompatibilno događaji je određen izrazom

Zaključak 1: Kompletna grupa događaja sastoji se od nespojivih događaja, od kojih se jedan nužno ostvaruje u iskustvu. Kao rezultat, ako događaji …
,formiraju kompletnu grupu, zatim za njih

dakle,

WITHposljedica 3 Uzmimo u obzir da će se suprotna tvrdnji „dogoditi barem jedan od događaja …
" je izjava "nijedan od događaja …
se ne implementira." To jest, drugim riječima, „događaji će se posmatrati u iskustvu , And , i..., i ”, koji već predstavlja presek događaja suprotnih originalnom skupu. Odavde, uzimajući u obzir (2.0), za kombinovanje proizvoljnog broja događaja dobijamo

Korolacije 2 i 3 pokazuju da je u slučajevima kada je direktno izračunavanje vjerovatnoće događaja problematično, korisno procijeniti složenost proučavanja suprotnog događaja. Uostalom, znajući značenje
, dobiti traženu vrijednost iz (2 .0)
više ne predstavlja nikakvu poteškoću.

    1. Primjeri izračunavanja vjerovatnoća složenih događaja

Primjer 1 : Dva učenika (Ivanov i Petrov) zajedno Istao u zaštitu laboratorijski rad, nakon što je naučio prvih 8 čunjevatrolling pitanja za ovaj rad od 10 dostupnih. Provjera spremnosti, strUčitelj pita svakoga samo jednon nasumično odabrano pitanje. Odredite vjerovatnoću sljedećih događaja:

A= “Ivanov će braniti svoj laboratorijski rad”;

B= “Petrov će braniti svoj laboratorijski rad”;

C= “obojica će braniti laboratorijski rad”;

D= „najmanje jedan od učenika će braniti rad“;

E= „samo jedan od učenika će braniti rad“;

F= "niko od njih neće zaštititi posao."

Rješenje. Imajte na umu da je sposobnost odbrane rad kao Ivanov, tkao i Petrova posebno određuje samo broj savladanih pitanja, dakleat. (Napomena: u u ovom primjeru vrijednosti dobivenih razlomaka nisu namjerno smanjene kako bi se pojednostavilo poređenje rezultata proračuna.)

DogađajCmože se formulisati drugačije jer će „i Ivanov i Petrov štititi delo“, tj. desiće seI događajA, I događajB. Dakle, događajCje presek događajaAIB, a u skladu sa (2 .0)

gdje se faktor “7/9” pojavljuje zbog činjenice da je pojava događajaAznači da je Ivanov dobio “uspješno” pitanje, što znači da Petrov sada ima samo 7 “dobrih” pitanja od preostalih 9 pitanja.

DogađajDimplicira da će „posao štititiili Ivanov,ili Petrov,ili oboje su zajedno”, tj. desiće se barem jedan od događajaAIB. Dakle, događajDje unija događajaAIB, a u skladu sa (2 .0)

koji ispunjava očekivanja, jer Čak i za svakog učenika pojedinačno, šanse za uspjeh su prilično velike.

WITHdogađaj E znači da će „ili Ivano zaštititi posaou, i Petrov „strpada"ili Ivanov će se loše provesti"Profesionalci, a Petrov može da se nosi sa odbranom." Dvije alternative se međusobno isključuju (nekompatibilne), dakle

Konačno, izjavaFbiće fer samo ako "I Ivanov,I Petrov sa zaštitomNe snaći će se." dakle,

Ovo dovršava rješenje problema, ali je korisno napomenuti sljedeće:

1. Svaka od dobijenih vjerovatnoća zadovoljava uslov (1 .0), noh ako za
I
dobiti sukobcosy with(1 .0) je nemoguće u principu, onda za
probaj ikorištenje (2 .0) umjesto (2.0) dovelo bi do očigledno netačnogznačenje projekta
. Važno je zapamtiti da je takva vrijednost vjerovatnoće u osnovi nemoguća, a ako dobijete tako paradoksalan rezultat, odmah počnite tražiti grešku.

2. Pronađene vjerovatnoće zadovoljavaju relacijem

.

Eovo je sasvim očekivano, jer događajiC, EIFformiraju kompletany grupa i događajiDIFsu suprotne jedna drugoj. Računovodstvo za ovemogu se koristiti omjeri s jedne stranekombi da još jednom provjeri proračune, au drugoj situaciji može poslužiti kao osnova za alternativni način rješavanja problema.

P Bilješka : Nemojte zanemariti pisanjeprecizna formulacija događaja, inače, u toku rješavanja problema, možete nehotice preći na drugačiju interpretaciju značenja ovog događaja, što će dovesti do grešaka u zaključivanju.

Primjer 2 : U velikoj seriji mikro krugova koji nisu prošli konačnu kontrolu kvaliteta, 30% proizvoda je neispravno.Ako nasumično odaberete bilo koja dva mikro kruga iz ove serije, šta je ondavjerovatnoća da je među njima:

A= “oba valjana”;

B= “tačno 1 upotrebljivo mikrokolo”;

C= “oba neispravna”.

Hajde da analiziramo sledeću verziju obrazloženja (pazi, sadrži grešku):

Budući da je riječ o velikoj seriji proizvoda, uklanjanje nekoliko mikro krugova iz nje praktički ne utječe na omjer broja upotrebljivih i neispravnih proizvoda, što znači da odabirom nekih mikro krugova iz ove serije nekoliko puta zaredom, mi može pretpostaviti da u svakom slučaju ostaju nepromijenjene vjerovatnoće

= P(odabran je neispravan proizvod) = 0,3 i

= P(odabran odgovarajući proizvod) = 0,7.

Da bi se događaj desioAto je neophodnoI kao prvo,I po drugi put je odabran odgovarajući proizvod, te stoga (uzimajući u obzir međusobno neovisnost uspješnosti izbora prvog i drugog mikrokola) za sjecište događaja imamo

Slično tome, da bi se dogodio događaj C, oba proizvoda moraju biti neispravna, a da biste dobili B, morate odabrati jedan dobar proizvod i jednom neispravan proizvod.

Znak greške. Xiako su svi dobili iznad vjerovatnoćei izgledaju uvjerljivo, kada se analiziraju zajedno, to je lakoImajte na umu da .Međutim, slučajeviA, BICformiraju kompletangrupa događaja za koje se treba izvršiti .Ova kontradikcija ukazuje da postoji neka greška u obrazloženju.

WITH postoje greške. Hajde da uvedemo dva pomoćnaspecijalni događaji:

= “prvo mikrokolo je dobro, drugo je neispravno”;

= "prvo mikrokolo je neispravno, drugo dobro."

Očigledno je da je, međutim, upravo ova opcija proračuna korištena gore za dobivanje vjerovatnoće događajaB, iako događajiBI nisu uhekvivalentno. Zapravo,
, jer formulacijadogađajiBzahtijeva da među mikro krugovima ima tačnojedan , ali nikakone nužno prvi bio dobar (a drugi je bio neispravan). Stoga, iako događaj nije duplikat događaja , ali treba ga podučavatida deluje samostalno. S obzirom na nespojivost događaja I , vjerovatnoća njihovog logičkog zbira će biti jednaka

Nakon naznačene korekcije proračuna imamo

što posredno potvrđuje ispravnost pronađenih vjerovatnoća.

Bilješka : Obratite posebnu pažnju na razliku u formulaciji događaja poput „samoprvo od navedenih elemenata mora…” i “samojedan od navedenih elemenataentov bi trebao...” Najnoviji događaj jasno širi i inkluzivanTu svoj sastav prvi kao jedan od (možda brojnihx) opcije. Ove alternative (čak i ako se njihove vjerovatnoće poklapaju) treba uzeti u obzir nezavisno jedna od druge.

P Bilješka : Riječ "postotak" dolazi od "per cent“, tj."na sto." Predstavljanje frekvencija i vjerovatnoća u postocima omogućava vam da radite s većim vrijednostima, što ponekad olakšava percepciju vrijednosti „na uho“. Međutim, korištenje množenja ili dijeljenja sa “100%” u proračunima za ispravnu normalizaciju je glomazno i ​​neefikasno. S tim u vezi, neBudite oprezni kada koristite vrijednosti koje treba spomenutiizražene u procentima, zamijenite ih u izračunate izraze zau obliku razlomaka jedinice (na primjer, 35% je upisano u proračunuSviđa mi se “0,35”) kako bi se smanjio rizik od pogrešne normalizacije rezultata.

Primjer 3 : Set otpornika sadrži jedan otpornik n4 kOhm nominalno, tri 8 kOhm otpornika i šest otpornikaili sa otporom od 15 kOhm. Tri nasumično odabrana otpornika su međusobno povezana paralelno. Odredite vjerovatnoću dobivanja konačnog otpora koji ne prelazi 4 kOhm.

Resh tion. Otpor paralelne vezehistorije se mogu izračunati korištenjem formule

.

Ovo vam omogućava da uvedete događaje kao što su

A= “odabrana su tri otpornika od 15 kOma” = “
”;

B= “indva otpornika od 15 kOhm i jedan otpornikm 8 kOhm” =“
”…

Kompletna grupa događaja koji odgovaraju uslovima problema takođe uključuje cela linija opcije, i to upravo one dokoji ispunjavaju navedeni zahtjev za postizanje otpora ne većeg od 4 kOhm. Međutim, iako je „direktan“ put rješenja, koji uključuje izračunavanje (i naknadne sumeIako je ispravno odrediti vjerovatnoće koje karakterišu sve ove događaje, nije preporučljivo postupati na ovaj način.

Imajte na umu da da biste dobili konačni otpor manji od 4 kOhm dDovoljno je da set sadrži najmanje jedan otpornik sa otporomJedem manje od 15 kOhm. Dakle, samo u slučajuAuslov zadatka nije ispunjen, tj. događajAjesuprotno osobi koja se proučava. U isto vrijeme,

.

Dakle, .

P ri označavanje : Izračunavanje vjerovatnoće nekog događajaA, ne zaboravite analizirati složenost određivanjaJa sam vjerovatnoća događaja suprotnog tome. Ako diss.čitaj
lako, onda je to tačno odakle treba da počnete, rešenoodnosno zadataka, dovršavajući ga primjenom relacije (2 .0).

P primjer 4 : U kutiji postojenbijela,mcrna ikcrvene lopte. Kuglice se nasumično izvlače iz kutije jedna po jedna.i vraćaju se nakon svake ekstrakcije. Odredite vjerovatnoćudogađajiA= „bijela loptaće biti izvučen prije crnog” .

Resh tion. Razmotrite sljedeći niz događaja

= “bijela lopta je izvučena iz prvog pokušaja”;

= “prvo je izvađena crvena lopta, a zatim bela”;

= “crvena lopta je izvađena dva puta, a bela treći put”…

Tako daKako se loptice vraćaju, onda nizyty može se formalno beskonačno produžiti.

Ovi događaji su nekompatibilni i zajedno čine skup situacija u kojima se događaj događaA. dakle,

Lako je vidjeti da su termini uključeni u zbirni oblikgeometrijska progresija sa početnim elementom
i imenilac
. Ali iznosia elementi beskonačne geometrijske progresije su jednaki

.

Dakle, . LZanimljivo je da ova vjerovatnoća (kako slijedi iz dobijenihth izraz) ne zavisi od broja crvenih loptica u kutiji.

Kratka teorija

Za kvantitativno upoređivanje događaja prema stepenu mogućnosti njihovog nastanka uvodi se numerička mjera koja se naziva vjerovatnoća događaja. Vjerovatnoća slučajnog događaja je broj koji izražava mjeru objektivne mogućnosti da se događaj dogodi.

Količine koje određuju koliko su značajni objektivni razlozi za očekivanje nastanka događaja karakteriziraju se vjerovatnoćom događaja. Mora se naglasiti da je vjerovatnoća objektivna veličina koja postoji nezavisno od poznavaoca i uslovljena je čitavim skupom uslova koji doprinose nastanku događaja.

Objašnjenja koja smo dali za koncept vjerovatnoće nisu matematička definicija, budući da ne definiraju ovaj koncept kvantitativno. Postoji nekoliko definicija vjerovatnoće slučajnog događaja, koje se široko koriste u rješavanju specifičnih problema (klasična, geometrijska definicija vjerovatnoće, statistička, itd.).

Klasična definicija vjerovatnoće događaja svodi ovaj koncept na elementarniji koncept jednako mogućih događaja, koji više nije podložan definiciji i pretpostavlja se da je intuitivno jasan. Na primjer, ako je kocka homogena kocka, tada će gubitak bilo kojeg lica ove kocke biti jednako mogući događaji.

Neka se pouzdani događaj podijeli na jednako moguće slučajeve, čiji zbir daje događaj. Odnosno, slučajevi na koje se raspada nazivaju se povoljnim za događaj, jer pojava jednog od njih osigurava nastanak.

Vjerovatnoća događaja će biti označena simbolom.

Vjerovatnoća događaja jednaka je odnosu broja slučajeva koji su za njega povoljni, od ukupnog broja jedinstveno mogućih, jednako mogućih i nespojivih slučajeva, prema broju, tj.

Ovo je klasična definicija vjerovatnoće. Dakle, da bi se pronašla vjerovatnoća događaja, potrebno je, s obzirom na različite ishode testa, pronaći skup jedinstveno mogućih, jednako mogućih i nekompatibilnih slučajeva, izračunati njihov ukupan broj n, broj slučajeva m povoljan za dati događaj, a zatim izvršite proračun koristeći gornju formulu.

Vjerovatnoća događaja jednak omjeru naziva se broj ishoda iskustva povoljnog za događaj na ukupan broj ishoda iskustva klasična verovatnoća slučajni događaj.

Iz definicije slijede sljedeća svojstva vjerovatnoće:

Svojstvo 1. Vjerovatnoća pouzdan događaj jednako jedan.

Svojstvo 2. Vjerovatnoća nemogući događaj jednaka nuli.

Svojstvo 3. Vjerovatnoća slučajnog događaja je pozitivan broj između nule i jedan.

Svojstvo 4. Vjerovatnoća pojave događaja koji čine kompletnu grupu jednaka je jedan.

Svojstvo 5. Vjerovatnoća pojave suprotnog događaja određuje se na isti način kao i vjerovatnoća nastanka događaja A.

Broj slučajeva koji favorizuju pojavu suprotnog događaja. Dakle, vjerovatnoća pojave suprotnog događaja jednaka je razlici između jedinice i vjerovatnoće pojave događaja A:

Važna prednost klasične definicije vjerovatnoće događaja je da se uz njenu pomoć vjerovatnoća događaja može odrediti bez pribjegavanja iskustvu, već na osnovu logičkog zaključivanja.

Kada se ispuni niz uslova, pouzdan događaj će se sigurno dogoditi, ali nemoguć događaj se definitivno neće dogoditi. Među događajima koji se mogu ili ne moraju dogoditi kada se stvori niz uslova, na pojavu nekih se može računati s dobrim razlogom, a na pojavu drugih s manje razloga. Ako, na primjer, ima više bijelih loptica u urni nego crnih, onda postoji više razloga da se nadamo pojavi bijele kugle kada se nasumično izvuče iz urne nego pojavi crne kugle.

Sljedeća stranica govori o tome.

Primjer rješenja problema

Primjer 1

Kutija sadrži 8 bijelih, 4 crne i 7 crvenih loptica. 3 kuglice se izvlače nasumično. Nađite vjerovatnoće sljedećih događaja: – izvučena je najmanje 1 crvena kugla, – postoje najmanje 2 kuglice iste boje, – ima najmanje 1 crvena i 1 bijela kugla.

Rješenje problema

Ukupan broj ishoda testa nalazimo kao broj kombinacija od 19 (8+4+7) elemenata od 3:

Nađimo vjerovatnoću događaja– izvučena je najmanje 1 crvena loptica (1,2 ili 3 crvene kuglice)

Potrebna vjerovatnoća:

Neka događaj– postoje najmanje 2 lopte iste boje (2 ili 3 bijele, 2 ili 3 crne i 2 ili 3 crvene lopte)

Broj ishoda povoljnih za događaj:

Potrebna vjerovatnoća:

Neka događaj– postoji najmanje jedna crvena i 1 bela lopta

(1 crvena, 1 bijela, 1 crna ili 1 crvena, 2 bijela ili 2 crvena, 1 bijela)

Broj ishoda povoljnih za događaj:

Potrebna vjerovatnoća:

odgovor: P(A)=0,773; P(C)=0,7688; P(D)=0,6068

Primjer 2

Dva bačena kockice. Pronađite vjerovatnoću da je zbir bodova najmanje 5.

Rješenje

Neka događaj bude rezultat najmanje 5

Koristimo klasičnu definiciju vjerovatnoće:

Ukupan broj mogućih ishoda testa

Broj pokušaja koji favorizuju događaj od interesa

Na ispuštenoj strani prve kocke može se pojaviti jedan bod, dva boda..., šest bodova. Slično, šest ishoda je moguće prilikom bacanja druge kocke. Svaki od ishoda bacanja prve kockice može se kombinirati sa svakim od ishoda druge. Dakle, ukupan broj mogućih ishoda elementarnog testa jednak je broju plasmana sa ponavljanjima (izbor sa plasmanima od 2 elementa iz skupa 6. volumena):

Nađimo vjerovatnoću suprotnog događaja - zbir bodova je manji od 5

Sljedeće kombinacije izgubljenih bodova će favorizirati događaj:

№ 1. kost 2nd kost 1 1 1 2 1 2 3 2 1 4 3 1 5 1 3

Na cijenu u velikoj mjeri utiče hitnost odluke (od jednog dana do nekoliko sati). Online pomoć oko ispita/testova dostupna je po dogovoru.

Zahtjev možete ostaviti direktno u chatu, nakon što ste prethodno poslali uslove zadataka i obavijestili vas o vremenskom okviru za rješenje koje vam je potrebno. Vrijeme odgovora je nekoliko minuta.

Kako izračunati vjerovatnoću događaja?

Razumijem da svi žele unaprijed znati kako će se sportski događaj završiti, ko će pobijediti, a ko izgubiti. Uz ove informacije možete se bez straha kladiti na sportske događaje. Ali da li je to uopšte moguće, i ako jeste, kako izračunati verovatnoću nekog događaja?

Vjerovatnoća je relativna vrijednost, stoga ne može sa sigurnošću govoriti ni o jednom događaju. Ova vrijednost vam omogućava da analizirate i procijenite potrebu da se kladite na određeno takmičenje. Određivanje vjerovatnoća je čitava nauka koja zahtijeva pažljivo proučavanje i razumijevanje.

Koeficijent vjerovatnoće u teoriji vjerovatnoće

U sportskom klađenju postoji nekoliko opcija za ishod takmičenja:

  • pobjeda prvog tima;
  • pobjeda drugog tima;
  • draw;
  • ukupno

Svaki ishod takmičenja ima svoju vjerovatnoću i učestalost s kojom će se ovaj događaj dogoditi, pod uslovom da se zadrže početne karakteristike. Kao što smo ranije rekli, nemoguće je precizno izračunati vjerovatnoću bilo kojeg događaja - može se, ali i ne mora podudarati. Dakle, vaša opklada može ili dobiti ili izgubiti.

Ne može postojati 100% tačna prognoza rezultata takmičenja, jer mnogo faktora utiče na ishod utakmice. Naravno, kladionice ne znaju unaprijed ishod utakmice i samo pretpostavljaju rezultat, donoseći odluke koristeći svoj sistem analize i nudeći određene kvote za klađenje.

Kako izračunati vjerovatnoću događaja?

Pretpostavimo da su kvote kladionice 2,1/2 – dobijamo 50%. Ispada da je koeficijent 2 jednak vjerovatnoći od 50%. Koristeći isti princip, možete dobiti koeficijent vjerovatnoće preloma - 1/vjerovatnoća.

Mnogi igrači misle da će se nakon nekoliko ponovljenih poraza sigurno dogoditi pobjeda - ovo je pogrešno mišljenje. Verovatnoća dobijanja opklade ne zavisi od broja gubitaka. Čak i ako okrenete nekoliko glava zaredom u igri novčića, vjerovatnoća okretanja repa ostaje ista - 50%.

Šta je vjerovatnoća?

Prvi put kada sam se susreo sa ovim terminom, ne bih razumeo šta je to. Stoga ću pokušati da objasnim jasno.

Vjerovatnoća je šansa da se dogodi događaj koji želimo.

Na primjer, odlučili ste otići kod prijatelja, sjećate se ulaza, pa čak i sprata na kojem živi. Ali sam zaboravio broj i lokaciju stana. A sada stojite na stepeništu, a ispred vas su vrata za izbor.

Koja je šansa (vjerovatnoća) da ako pozvonite na prva vrata, vaš prijatelj otvori vrata umjesto vas? Postoje samo stanovi, a samo iza jednog od njih živi prijatelj. Uz jednake šanse možemo izabrati bilo koja vrata.

Ali kakva je ovo šansa?

Vrata, desna vrata. Vjerovatnoća pogađanja zvonjavom na prva vrata: . Odnosno, jednom od tri tačno ćete pogoditi.

Želimo znati, nakon što smo jednom pozvali, koliko često ćemo pogoditi vrata? Pogledajmo sve opcije:

  1. Zvao si 1st vrata
  2. Zvao si 2nd vrata
  3. Zvao si 3rd vrata

Sada pogledajmo sve opcije gdje bi prijatelj mogao biti:

A. Iza 1st vrata
b. Iza 2nd vrata
V. Iza 3rd vrata

Uporedimo sve opcije u obliku tabele. Kvačica označava opcije kada se vaš izbor poklapa sa lokacijom prijatelja, križić - kada se ne poklapa.

Kako vidite sve Možda opcije lokacija vašeg prijatelja i vaš izbor na koja vrata ćete zvoniti.

A povoljni ishodi svih . Odnosno, jednom ćete pogoditi tako što ćete jednom pozvoniti na vrata, tj. .

Ovo je vjerovatnoća - omjer povoljnog ishoda (kada se vaš izbor poklopi sa lokacijom vašeg prijatelja) i broja mogućih događaja.

Definicija je formula. Verovatnoća se obično označava sa p, pa:

Nije baš zgodno napisati takvu formulu, pa ćemo za - broj povoljnih ishoda uzeti, a za - ukupan broj ishoda.

Vjerovatnoća se može napisati kao postotak; da biste to učinili, trebate pomnožiti rezultirajući rezultat sa:

Vjerovatno vam je zapela za oko riječ „ishodi“. Jer matematičari zovu razne akcije(kod nas je takva radnja zvono na vratima) eksperimente, onda se rezultat takvih eksperimenata obično naziva ishod.

Pa, ima povoljnih i nepovoljnih ishoda.

Vratimo se na naš primjer. Recimo da smo pozvonili na jedna vrata, ali su nam otvorena stranac. Nismo pogodili. Kolika je vjerovatnoća da će nam prijatelj otvoriti ako pozvonimo na neka od preostalih vrata?

Ako ste tako mislili, onda je ovo greška. Hajde da to shvatimo.

Ostala su nam dvoja vrata. Dakle, imamo moguće korake:

1) Pozovite 1st vrata
2) Pozovite 2nd vrata

Prijatelj, i pored svega ovoga, definitivno stoji iza jednog od njih (uostalom, nije stajao iza onoga koga smo zvali):

a) Prijatelj za 1st vrata
b) Prijatelj za 2nd vrata

Ponovo nacrtajmo tabelu:

Kao što vidite, postoje samo opcije, od kojih su povoljne. Odnosno, vjerovatnoća je jednaka.

Zašto ne?

Situacija koju smo razmatrali jeste primjer zavisnih događaja. Prvi događaj je prvo zvono na vratima, drugi događaj je drugo zvono na vratima.

A nazivaju se zavisnim jer utiču na sledeće radnje. Na kraju krajeva, ako bi se nakon prvog zvona na vrata javio prijatelj, kolika bi bila vjerovatnoća da je on bio iza jednog od druga dva? U redu, .

Ali ako postoje zavisni događaji, onda ih također moraju postojati nezavisni? Tako je, dešavaju se.

Primjer iz udžbenika je bacanje novčića.

  1. Baci novčić jednom. Kolika je vjerovatnoća da dobijete glave, na primjer? Tako je - jer postoje sve opcije (bilo glave ili repa, zanemarićemo vjerovatnoću da novčić sleti na njegovu ivicu), ali samo nama to odgovara.
  2. Ali to je palo na pamet. Ok, bacimo ga ponovo. Kolika je vjerovatnoća da sada dobijete glave? Ništa se nije promenilo, sve je isto. Koliko opcija? Dva. Sa koliko smo zadovoljni? Jedan.

I neka se pojavi barem hiljadu puta zaredom. Vjerovatnoća da dobijete glave odjednom će biti ista. Uvek postoje opcije, i to povoljne.

Lako je razlikovati zavisne događaje od nezavisnih:

  1. Ako se eksperiment izvede jednom (jednom baci novčić, jednom pozvoni na vrata itd.), događaji su uvijek nezavisni.
  2. Ako se eksperiment izvodi nekoliko puta (jednom se baci novčić, nekoliko puta se zvoni na vratima), tada je prvi događaj uvijek nezavisan. A onda, ako se promijeni broj povoljnih ili broj svih ishoda, onda su događaji zavisni, a ako ne, nezavisni.

Hajde da malo vežbamo određivanje verovatnoće.

Primjer 1.

Novčić se baca dva puta. Kolika je vjerovatnoća da dobijete glave dva puta zaredom?

Rješenje:

Hajde da razmotrimo sve moguće opcije:

  1. Eagle-eagle
  2. Glava-rep
  3. Tails-Heads
  4. Repovi-repovi

Kao što vidite, postoje samo opcije. Od ovih smo samo zadovoljni. Odnosno, vjerovatnoća:

Ako uvjet traži jednostavno pronalaženje vjerovatnoće, onda odgovor treba dati u obliku decimalni. Kada bi se preciziralo da odgovor treba dati u procentima, onda bismo pomnožili sa.

odgovor:

Primjer 2.

U kutiji čokolade, sve čokolade su upakovane u isti omot. Međutim, od slatkiša - sa orasima, sa konjakom, sa višnjama, sa karamelom i sa nugatom.

Kolika je vjerovatnoća da uzmete jedan slatkiš i dobijete bombon sa orasima? Odgovor dajte u procentima.

Rješenje:

Koliko je mogućih ishoda? .

Odnosno, ako uzmete jedan slatkiš, to će biti jedan od dostupnih u kutiji.

Koliko je povoljnih ishoda?

Jer kutija sadrži samo čokolade sa orasima.

odgovor:

Primjer 3.

U kutiji balona. od kojih su bijele i crne.

  1. Kolika je vjerovatnoća da izvučete bijelu loptu?
  2. Dodali smo još crnih loptica u kutiju. Kolika je sada vjerovatnoća da izvučete bijelu loptu?

Rješenje:

a) U kutiji su samo lopte. Od njih su bijeli.

Vjerovatnoća je:

b) Sada ima više loptica u kutiji. I belaca je ostalo isto toliko - .

odgovor:

Potpuna vjerovatnoća

Vjerovatnoća svih mogućih događaja jednaka je ().

Recimo da se u kutiji nalaze crvene i zelene kuglice. Kolika je vjerovatnoća da se izvuče crvena kugla? Zelena lopta? Crvena ili zelena lopta?

Verovatnoća izvlačenja crvene lopte

zelena lopta:

Crvena ili zelena lopta:

Kao što vidite, zbir svih mogućih događaja je jednak (). Razumijevanje ove tačke pomoći će vam da riješite mnoge probleme.

Primjer 4.

U kutiji se nalaze markeri: zeleni, crveni, plavi, žuti, crni.

Kolika je vjerovatnoća da NE nacrtate crveni marker?

Rješenje:

Hajde da izbrojimo broj povoljni ishodi.

NIJE crveni marker, to znači zeleno, plavo, žuto ili crno.

Vjerovatnoća svih događaja. A vjerovatnoća događaja koje smatramo nepovoljnim (kada izvadimo crveni marker) je .

Dakle, vjerovatnoća da ćete izvući NE crveni flomaster je .

odgovor:

Vjerovatnoća da se događaj neće dogoditi jednaka je minus vjerovatnoći da će se događaj dogoditi.

Pravilo za množenje vjerovatnoća nezavisnih događaja

Već znate šta su nezavisni događaji.

Šta ako trebate pronaći vjerovatnoću da će se dva (ili više) nezavisnih događaja dogoditi zaredom?

Recimo da želimo da znamo kolika je verovatnoća da ćemo, ako jednom bacimo novčić, dvaput videti glave?

Već smo razmotrili - .

Šta ako jednom bacimo novčić? Kolika je vjerovatnoća da ćete vidjeti orla dvaput zaredom?

Ukupno mogućih opcija:

  1. Eagle-eagle-eagle
  2. Glava-glava-rep
  3. Glava-repa-glava
  4. Glava-repa-repa
  5. Repovi-glave-glave
  6. Repovi-glavi-repovi
  7. Repovi-repovi-glave
  8. Repovi-repovi-repovi

Ne znam za vas, ali ja sam nekoliko puta pogriješio prilikom sastavljanja ove liste. Vau! I jedina opcija (prva) nam odgovara.

Za 5 bacanja možete sami napraviti listu mogućih ishoda. Ali matematičari nisu tako vredni kao vi.

Stoga su prvo uočili, a zatim dokazali da se vjerovatnoća određenog niza nezavisnih događaja svaki put smanjuje za vjerovatnoću jednog događaja.

Drugim riječima,

Pogledajmo primjer istog nesretnog novčića.

Vjerovatnoća da ćete dobiti glave u izazovu? . Sada bacamo novčić jednom.

Kolika je vjerovatnoća da dobijete glave u nizu?

Ovo pravilo ne funkcioniše samo ako se od nas traži da pronađemo verovatnoću da će se isti događaj desiti nekoliko puta zaredom.

Kada bismo hteli da pronađemo sekvencu REPOVI-GLAVE-REPOVI za uzastopna bacanja, uradili bismo isto.

Vjerovatnoća slijetanja glava je - , glava - .

Verovatnoća dobijanja sekvence REP-GLAVE-REPOVI-REPOVI:

To možete sami provjeriti tako što ćete napraviti tabelu.

Pravilo za sabiranje vjerovatnoća nekompatibilnih događaja.

Zato prestani! Nova definicija.

Hajde da to shvatimo. Uzmimo naš istrošeni novčić i bacimo ga jednom.
Moguće opcije:

  1. Eagle-eagle-eagle
  2. Glava-glava-rep
  3. Glava-repa-glava
  4. Glava-repa-repa
  5. Repovi-glave-glave
  6. Repovi-glavi-repovi
  7. Repovi-repovi-glave
  8. Repovi-repovi-repovi

Dakle, nespojivi događaji su određeni, dati niz događaja. - ovo su nespojivi događaji.

Ako želimo da utvrdimo kolika je verovatnoća dva (ili više) nekompatibilnih događaja, onda sabiramo verovatnoće tih događaja.

Morate shvatiti da su glava ili rep dva nezavisna događaja.

Ako želimo da odredimo verovatnoću da će se niz (ili bilo koji drugi) pojaviti, onda koristimo pravilo množenja verovatnoća.
Kolika je vjerovatnoća da dobijete glavu pri prvom bacanju, a repove pri drugom i trećem bacanju?

Ali ako želimo da znamo kolika je verovatnoća da dobijemo jednu od nekoliko sekvenci, na primer, kada se glave pojave tačno jednom, tj. opcije i tada moramo sabrati vjerovatnoće ovih nizova.

Ukupne opcije nam odgovaraju.

Istu stvar možemo dobiti ako zbrojimo vjerovatnoće pojavljivanja svakog niza:

Stoga, dodajemo vjerovatnoće kada želimo da odredimo vjerovatnoću određenih, nekonzistentnih slijeda događaja.

Postoji odlično pravilo koje će vam pomoći da izbjegnete zabunu kada množiti, a kada sabirati:

Vratimo se na primjer gdje smo jednom bacili novčić i htjeli znati vjerovatnoću da ćemo jednom vidjeti glave.
Šta će se dogoditi?

Trebalo bi ispasti:
(glave I repovi I repovi) ILI (repovi I glave I repovi) OR (repovi I repovi I glave).
Ovako ispada:

Pogledajmo nekoliko primjera.

Primjer 5.

U kutiji su olovke. crvena, zelena, narandžasta i žuta i crna. Kolika je vjerovatnoća da ćete nacrtati crvene ili zelene olovke?

Rješenje:

Šta će se dogoditi? Moramo povući (crveno ILI zeleno).

Sada je jasno, hajde da zbrojimo vjerovatnoće ovih događaja:

odgovor:

Primjer 6.

Ako je kocka bačena dvaput, kolika je vjerovatnoća da ćete dobiti ukupno 8?

Rješenje.

Kako možemo dobiti bodove?

(i) ili (i) ili (i) ili (i) ili (i).

Vjerovatnoća da dobijete jedno (bilo koje) lice je .

Izračunavamo vjerovatnoću:

odgovor:

Trening.

Mislim da sada razumete kada treba da izračunate verovatnoće, kada da ih dodate, a kada da ih pomnožite. Nije li? Vježbajmo malo.

Zadaci:

Uzmimo špil karata koji sadrži karte uključujući pikove, srca, 13 trefa i 13 karata. Od do Asa svake boje.

  1. Kolika je vjerovatnoća da izvučemo štafete u nizu (prvu izvučenu kartu vratimo u špil i promiješamo je)?
  2. Kolika je vjerovatnoća izvlačenja crne karte (pik ili trefa)?
  3. Kolika je vjerovatnoća da se izvuče slika (valet, dama, kralj ili as)?
  4. Kolika je vjerovatnoća da se izvuku dvije slike za redom (uklanjamo prvu izvučenu kartu iz špila)?
  5. Kolika je vjerovatnoća da se, uzimajući dvije karte, sakupi kombinacija - (jack, dama ili kralj) i as? Redoslijed u kojem se karte izvlače nije bitan.

odgovori:

  1. U špilu karata svake vrijednosti to znači:
  2. Događaji su zavisni, jer se nakon izvlačenja prve karte smanjio broj karata u špilu (kao i broj „slika“). Na početku u špilu ima ukupnih džakova, dama, kraljeva i asova, što znači vjerovatnoću izvlačenja "slike" s prvom kartom:

    S obzirom da uklanjamo prvu kartu iz špila, to znači da su u špilu već ostale karte, uključujući slike. Verovatnoća crtanja slike sa drugom karticom:

    Budući da nas zanima situacija kada iz špila izvadimo „sliku“ I „sliku“, trebamo pomnožiti vjerovatnoće:

    odgovor:

  3. Nakon što se izvuče prva karta, broj karata u špilu će se smanjiti, tako da nam odgovaraju dvije opcije:
    1) Prva karta je as, druga je Jack, Queen ili King
    2) Prvom kartom vadimo džanca, damu ili kralja, a drugom asa. (kec i (valet ili dama ili kralj)) ili ((valet ili dama ili kralj) i as). Ne zaboravite na smanjenje broja karata u špilu!

Ako ste uspjeli sami riješiti sve probleme, onda ste odlični! Sada ćete kao ludi razbijati probleme teorije vjerovatnoće na Jedinstvenom državnom ispitu!

TEORIJA VEROVATNOSTI. PROSJEČAN NIVO

Pogledajmo primjer. Recimo da bacimo kocku. Kakva je ovo kost, znaš li? To je ono što zovu kocka sa brojevima na licu. Koliko lica, toliko brojeva: od do koliko? Prije.

Dakle, bacamo kockice i želimo da ispadne ili. I shvatili smo.

U teoriji vjerovatnoće kažu šta se dogodilo povoljan događaj(ne brkati sa prosperitetnim).

Da se to dogodi, događaj bi takođe bio povoljan. Ukupno se mogu desiti samo dva povoljna događaja.

Koliko je nepovoljnih? Pošto ima ukupno mogućih događaja, to znači da su oni nepovoljni događaji (ovo je ako ili ispadne).

definicija:

Vjerovatnoća je omjer broja povoljnih događaja i broja svih mogućih događaja. Odnosno, vjerovatnoća pokazuje koliki je udio svih mogućih događaja povoljan.

Vjerovatnoća je označena latiničnim slovom (iz engleska riječ vjerovatnoća - vjerovatnoća).

Uobičajeno je da se vjerovatnoća mjeri u procentima (pogledajte teme i). Da biste to učinili, vrijednost vjerovatnoće se mora pomnožiti sa. U primjeru s kockicama, vjerovatnoća.

I u procentima: .

Primjeri (odlučite sami):

  1. Kolika je vjerovatnoća da dobijete glavu prilikom bacanja novčića? Kolika je vjerovatnoća sletanja glava?
  2. Kolika je vjerovatnoća da dobijete kada bacate kocku čak broj? Koji je čudan?
  3. U kutiji jednostavnih, plavih i crvenih olovaka. Nasumce crtamo jednu olovku. Kolika je vjerovatnoća da dobijete jednostavnu?

rješenja:

  1. Koliko opcija postoji? Glava i rep - samo dva. Koliko ih je povoljnih? Samo jedan je orao. Dakle, vjerovatnoća

    Isto je i sa repovima: .

  2. Ukupno opcija: (koliko strana ima kocka, toliko različitih opcija). Povoljni: (ovo su sve parni brojevi:).
    Vjerovatnoća. Naravno, isto je i sa neparnim brojevima.
  3. Ukupno: . Povoljno: . Verovatnoća: .

Potpuna vjerovatnoća

Sve olovke u kutiji su zelene. Kolika je vjerovatnoća da ćete nacrtati crvenu olovku? Nema šanse: vjerovatnoća (na kraju krajeva, povoljni događaji -).

Takav događaj se naziva nemogućim.

Kolika je vjerovatnoća da nacrtate zelenu olovku? Postoji potpuno isti broj povoljnih događaja koliko i ukupnih događaja (svi događaji su povoljni). Dakle, vjerovatnoća je jednaka ili.

Takav se događaj naziva pouzdanim.

Ako kutija sadrži zelene i crvene olovke, kolika je vjerovatnoća da ćete nacrtati zelenu ili crvenu? Još jednom. Zapazimo ovo: vjerovatnoća izvlačenja zelene je jednaka, a crvene je jednaka.

Sve u svemu, ove vjerovatnoće su potpuno jednake. To je, zbir vjerovatnoća svih mogućih događaja jednak je ili.

primjer:

U kutiji olovaka, među njima su plave, crvene, zelene, obične, žute, a ostale su narandžaste. Kolika je vjerovatnoća da ne nacrtate zeleno?

Rješenje:

Sjećamo se da se sve vjerovatnoće sabiraju. I vjerovatnoća da dobijete zelenu boju je jednaka. To znači da je vjerovatnoća da se ne izvuče zeleno jednaka.

Zapamtite ovaj trik: Vjerovatnoća da se događaj neće dogoditi jednaka je minus vjerovatnoći da će se događaj dogoditi.

Nezavisni događaji i pravilo množenja

Bacate novčić jednom i želite da oba puta padne na glavu. Koja je vjerovatnoća za ovo?

Prođimo kroz sve moguće opcije i odredimo koliko ih ima:

Glave-glave, repove-glave, glave-repe, repove-repove. Šta još?

Total options. Od njih nam samo jedan odgovara: Orao-Orao. Ukupno, vjerovatnoća je jednaka.

U redu. Sada bacimo novčić jednom. Izračunaj sam. Desilo se? (odgovor).

Možda ste primijetili da se sa dodavanjem svakog sljedećeg bacanja vjerovatnoća smanjuje za polovicu. Opšte pravilo pozvao pravilo množenja:

Vjerovatnoće nezavisnih događaja se mijenjaju.

Šta su nezavisni događaji? Sve je logično: to su oni koji ne zavise jedni od drugih. Na primjer, kada bacimo novčić nekoliko puta, svaki put se izvrši novo bacanje, čiji rezultat ne ovisi o svim prethodnim bacanjima. Isto tako lako možemo baciti dva različita novčića u isto vrijeme.

Više primjera:

  1. Kockice se bacaju dva puta. Kolika je vjerovatnoća da dobijete oba puta?
  2. Novčić se baca jednom. Kolika je vjerovatnoća da će prvi put iskrsnuti, a zatim dva puta ispasti?
  3. Igrač baca dvije kockice. Kolika je vjerovatnoća da će zbir brojeva na njima biti jednak?

odgovori:

  1. Događaji su nezavisni, što znači da pravilo množenja radi: .
  2. Vjerovatnoća glava je jednaka. Vjerovatnoća repova je ista. pomnožiti:
  3. 12 se može dobiti samo ako se bacaju dva -ki: .

Nekompatibilni događaji i pravilo zbrajanja

Događaji koji se međusobno nadopunjuju do pune vjerovatnoće nazivaju se nekompatibilnim. Kao što ime govori, ne mogu se desiti istovremeno. Na primjer, ako bacimo novčić, može se pojaviti ili glava ili rep.

Primjer.

U kutiji olovaka, među njima su plave, crvene, zelene, obične, žute, a ostale su narandžaste. Kolika je vjerovatnoća da ćete nacrtati zeleno ili crveno?

Rješenje .

Vjerovatnoća da se nacrta zelena olovka je jednaka. Crvena - .

Povoljni događaji u svemu: zeleno + crveno. To znači da je vjerovatnoća izvlačenja zelene ili crvene boje jednaka.

Ista vjerovatnoća se može predstaviti u ovom obliku: .

Ovo je pravilo dodavanja: vjerovatnoće nekompatibilnih događaja se zbrajaju.

Problemi mješovitog tipa

Primjer.

Novčić se baca dva puta. Kolika je vjerovatnoća da će rezultati probijanja biti drugačiji?

Rješenje .

To znači da ako je prvi rezultat glava, drugi mora biti rep, i obrnuto. Ispostavilo se da postoje dva para nezavisnih događaja, a ti parovi su međusobno nekompatibilni. Kako se ne zbuniti oko toga gdje pomnožiti, a gdje dodati.

Za takve situacije postoji jednostavno pravilo. Pokušajte opisati šta će se dogoditi koristeći veznike “I” ili “ILI”. Na primjer, u ovom slučaju:

Trebalo bi doći gore (glave i repovi) ili (repovi i glave).

Tamo gdje postoji veznik "i" bit će množenje, a gdje je "ili" bit će zbrajanje:

Probajte sami:

  1. Kolika je vjerovatnoća da će, ako se novčić baci dva puta, novčić oba puta pasti na istu stranu?
  2. Kockice se bacaju dva puta. Kolika je vjerovatnoća da dobijete ukupan broj bodova?

rješenja:

  1. (Glave su pale i repovi su padali) ili (repovi su pali i repovi su padali): .
  2. Koje su opcije? I. onda:
    Ispušteno (i) ili (i) ili (i): .

Drugi primjer:

Baci novčić jednom. Kolika je vjerovatnoća da će se glave pojaviti barem jednom?

Rješenje:

O, kako ne želim da prolazim kroz opcije... Glava-rep-rep, Orao-glav-rep,... Ali nema potrebe! Prisjetimo se ukupne vjerovatnoće. Sjećaš li se? Kolika je vjerovatnoća da je orao nikada neće ispasti? Jednostavno: glave stalno lete, eto zašto.

TEORIJA VEROVATNOSTI. UKRATKO O GLAVNIM STVARIMA

Vjerovatnoća je omjer broja povoljnih događaja i broja svih mogućih događaja.

Nezavisni događaji

Dva događaja su nezavisna ako pojava jednog ne mijenja vjerovatnoću da se drugi dogodi.

Potpuna vjerovatnoća

Vjerovatnoća svih mogućih događaja jednaka je ().

Vjerovatnoća da se događaj neće dogoditi jednaka je minus vjerovatnoći da će se događaj dogoditi.

Pravilo za množenje vjerovatnoća nezavisnih događaja

Vjerovatnoća određenog niza nezavisnih događaja jednaka je proizvodu vjerovatnoća svakog događaja

Nekompatibilni događaji

Nekompatibilni događaji su oni koji se ne mogu dogoditi istovremeno kao rezultat eksperimenta. Brojni nekompatibilni događaji čine kompletnu grupu događaja.

Vjerovatnoće nekompatibilnih događaja se zbrajaju.

Nakon što smo opisali šta bi se trebalo dogoditi, koristeći veznike “AND” ili “OR”, umjesto “AND” stavljamo znak množenja, a umjesto “OR” stavljamo znak za sabiranje.

“Nesreće nisu slučajne”... Zvuči kao nešto što je filozof rekao, ali u stvari, proučavanje slučajnosti je sudbina velike nauke matematike. U matematici se slučajnošću bavi teorija vjerovatnoće. U članku će biti predstavljene formule i primjeri zadataka, kao i osnovne definicije ove nauke.

Šta je teorija vjerovatnoće?

Teorija vjerovatnoće je jedna od matematičkih disciplina koja proučava slučajne događaje.

Da bude malo jasnije, dajmo mali primjer: ako bacite novčić gore, on može pasti na glavu ili rep. Dok je novčić u zraku, obje ove vjerovatnoće su moguće. Odnosno, vjerovatnoća mogućih posljedica je 1:1. Ako se jedna izvuče iz špila od 36 karata, tada će vjerovatnoća biti označena kao 1:36. Čini se da se ovdje nema šta istraživati ​​i predviđati, posebno uz pomoć matematičkih formula. Međutim, ako određenu radnju ponovite mnogo puta, možete identificirati određeni obrazac i na osnovu njega predvidjeti ishod događaja u drugim uvjetima.

Da sumiramo sve navedeno, teorija vjerovatnoće u klasičnom smislu proučava mogućnost pojave jednog od mogućih događaja u numeričkoj vrijednosti.

Sa stranica istorije

Teorija vjerojatnosti, formule i primjeri prvih zadataka pojavili su se u dalekom srednjem vijeku, kada su se prvi put pojavili pokušaji predviđanja ishoda kartaških igara.

U početku, teorija vjerovatnoće nije imala nikakve veze s matematikom. To je bilo opravdano empirijskim činjenicama ili svojstvima događaja koji su se mogli reproducirati u praksi. Prvi radovi u ovoj oblasti kao u matematička disciplina pojavio u 17. veku. Osnivači su bili Blaise Pascal i Pierre Fermat. Dugo vrijeme proučavali su kockanje i vidjeli određene obrasce, o kojima su odlučili reći društvu.

Istu tehniku ​​je izmislio Christiaan Huygens, iako nije bio upoznat s rezultatima istraživanja Pascala i Fermata. On je uveo koncept „teorije vjerovatnoće“, formule i primjere koji se smatraju prvima u historiji discipline.

Radovi Jacoba Bernoullija, Laplaceove i Poissonove teoreme takođe su od velikog značaja. Učinili su teoriju vjerovatnoće više kao matematičku disciplinu. Teorija vjerojatnosti, formule i primjeri osnovnih zadataka dobili su svoj današnji oblik zahvaljujući Kolmogorovljevim aksiomima. Kao rezultat svih promjena, teorija vjerovatnoće je postala jedna od matematičkih grana.

Osnovni koncepti teorije vjerovatnoće. Događaji

Glavni koncept ove discipline je “događaj”. Postoje tri vrste događaja:

  • Pouzdan. One koje će se ipak dogoditi (novčić će pasti).
  • Nemoguće. Događaji koji se neće dogoditi ni pod kojim okolnostima (novčić će ostati visjeti u zraku).
  • Slučajno. One koje će se desiti ili se neće desiti. Na njih mogu uticati različiti faktori koje je vrlo teško predvidjeti. Ako govorimo o novčiću, onda slučajni faktori koji mogu utjecati na rezultat: fizičke karakteristike kovanice, njihov oblik, početni položaj, sila bacanja itd.

Svi događaji u primjerima su označeni velikim latiničnim slovima, osim P, koje ima drugačiju ulogu. Na primjer:

  • A = "studenti su došli na predavanje."
  • Ā = “studenti nisu došli na predavanje.”

IN praktični zadaci Događaji se obično bilježe riječima.

Jedna od najvažnijih karakteristika događaja je njihova jednaka mogućnost. Odnosno, ako bacite novčić, moguće su sve varijante početnog pada dok ne padne. Ali događaji takođe nisu podjednako mogući. Ovo se dešava kada neko namerno utiče na ishod. Na primjer, "označeno" karte za igranje ili kockice, u kojoj centar pomaknut gravitacije.

Događaji također mogu biti kompatibilni i nekompatibilni. Kompatibilni događaji ne isključuju pojavu jedni drugih. Na primjer:

  • A = "student je došao na predavanje."
  • B = "student je došao na predavanje."

Ovi događaji su nezavisni jedan od drugog i pojava jednog od njih ne utiče na pojavu drugog. Nekompatibilni događaji su definisani činjenicom da pojava jednog isključuje pojavu drugog. Ako govorimo o istom novčiću, onda gubitak "repova" onemogućava pojavu "glava" u istom eksperimentu.

Akcije na događaje

Događaji se mogu množiti i sabirati, shodno tome se u disciplinu uvode logički spojevi „I“ i „ILI“.

Iznos je određen činjenicom da se ili događaj A ili B, ili dva, mogu dogoditi istovremeno. Ako su nekompatibilni, posljednja opcija je nemoguća; ili A ili B će biti izbačeni.

Umnožavanje događaja se sastoji u pojavi A i B u isto vrijeme.

Sada možemo dati nekoliko primjera kako bismo bolje zapamtili osnove, teoriju vjerojatnosti i formule. Primjeri rješavanja problema u nastavku.

Vježba 1: Kompanija učestvuje na konkursu za dobijanje ugovora za tri vrste radova. Mogući događaji koji se mogu dogoditi:

  • A = "firma će dobiti prvi ugovor."
  • A 1 = "firma neće primiti prvi ugovor."
  • B = "firma će dobiti drugi ugovor."
  • B 1 = “firma neće dobiti drugi ugovor”
  • C = "firma će dobiti treći ugovor."
  • C 1 = "firma neće dobiti treći ugovor."

Koristeći akcije na događaje, pokušat ćemo izraziti sljedeće situacije:

  • K = “kompanija će dobiti sve ugovore.”

IN matematički oblik jednačina će imati sljedeći oblik: K = ABC.

  • M = “kompanija neće dobiti nijedan ugovor.”

M = A 1 B 1 C 1.

Hajde da zakomplikujemo zadatak: H = "kompanija će dobiti jedan ugovor." Kako se ne zna koji će ugovor kompanija dobiti (prvi, drugi ili treći), potrebno je zabilježiti cijeli niz mogućih događaja:

H = A 1 BC 1 υ AB 1 C 1 υ A 1 B 1 C.

A 1 BC 1 je niz događaja u kojima firma ne prima prvi i treći ugovor, ali prima drugi. Drugi mogući događaji snimljeni su odgovarajućom metodom. Simbol υ u disciplini označava vezu "ILI". Ako gornji primjer prevedemo na ljudski jezik, kompanija će dobiti ili treći ugovor, ili drugi, ili prvi. Na sličan način možete zapisati i druge uslove u disciplini “Teorija vjerovatnoće”. Gore navedene formule i primjeri rješavanja problema pomoći će vam da to učinite sami.

Zapravo, vjerovatnoća

Možda je u ovoj matematičkoj disciplini vjerovatnoća događaja centralni koncept. Postoje 3 definicije vjerovatnoće:

  • klasična;
  • statistički;
  • geometrijski.

Svaki od njih ima svoje mjesto u proučavanju vjerovatnoće. Teorija vjerojatnosti, formule i primjeri (9. razred) uglavnom koriste klasičnu definiciju, koja zvuči ovako:

  • Vjerovatnoća situacije A jednaka je omjeru broja ishoda koji pogoduju njenom nastanku i broja svih mogućih ishoda.

Formula izgleda ovako: P(A)=m/n.

A je zapravo događaj. Ako se pojavi slučaj suprotan od A, može se napisati kao Ā ili A 1 .

m je broj mogućih povoljnih slučajeva.

n - svi događaji koji se mogu dogoditi.

Na primjer, A = "izvuci kartu srčane boje." U standardnom špilu ima 36 karata, od kojih je 9 od srca. U skladu s tim, formula za rješavanje problema će izgledati ovako:

P(A)=9/36=0,25.

Kao rezultat toga, vjerovatnoća da će karta srčane boje biti izvučena iz špila bit će 0,25.

Ka višoj matematici

Sada je postalo malo poznato šta je teorija vjerovatnoće, formule i primjeri rješavanja problema koji se pojavljuju školski program. Međutim, teorija vjerovatnoće se nalazi iu višoj matematici, koja se predaje na univerzitetima. Najčešće operišu geometrijskim i statističkim definicijama teorije i složenim formulama.

Teorija vjerovatnoće je veoma interesantna. Bolje je početi proučavati formule i primjere (viša matematika) male - sa statističkom (ili frekvencijskom) definicijom vjerovatnoće.

Statistički pristup nije u suprotnosti sa klasičnim, ali ga neznatno proširuje. Ako je u prvom slučaju bilo potrebno odrediti s kojom vjerovatnoćom će se događaj dogoditi, onda je u ovoj metodi potrebno naznačiti koliko će se često događati. Ovdje se uvodi novi koncept “relativne frekvencije” koji se može označiti sa W n (A). Formula se ne razlikuje od klasične:

Ako se za predviđanje izračunava klasična formula, onda se statistička izračunava prema rezultatima eksperimenta. Uzmimo za primjer mali zadatak.

Odjel za tehnološku kontrolu provjerava kvalitetu proizvoda. Među 100 proizvoda utvrđeno je da su 3 loše kvalitete. Kako pronaći vjerovatnoću frekvencije kvalitetnog proizvoda?

A = "izgled kvalitetnog proizvoda."

W n (A)=97/100=0,97

Dakle, frekvencija kvalitetnog proizvoda je 0,97. Odakle ti 97? Od 100 proizvoda koji su provjereni, utvrđeno je da su 3 proizvoda lošeg kvaliteta. Od 100 oduzimamo 3 i dobijemo 97, ovo je količina kvalitetne robe.

Malo o kombinatorici

Druga metoda teorije vjerovatnoće naziva se kombinatorika. Njegov osnovni princip je da ako se određeni izbor A može napraviti m Različiti putevi, a izbor B je na n različitih načina, onda se izbor A i B može obaviti množenjem.

Na primjer, postoji 5 puteva koji vode od grada A do grada B. Postoje 4 puta od grada B do grada C. Na koliko načina možete stići od grada A do grada C?

Jednostavno je: 5x4=20, odnosno na dvadeset različitih načina možete doći od tačke A do tačke C.

Hajde da zakomplikujemo zadatak. Na koliko načina postoji polaganje karata u pasijansu? U špilu se nalazi 36 karata - ovo je početna tačka. Da biste saznali broj načina, morate „oduzeti“ jednu po jednu kartu od početne tačke i množiti.

To jest, 36x35x34x33x32...x2x1= rezultat ne stane na ekran kalkulatora, tako da se jednostavno može označiti kao 36!. Potpišite "!" pored broja označava da se cijeli niz brojeva množi zajedno.

U kombinatorici postoje koncepti kao što su permutacija, smještaj i kombinacija. Svaki od njih ima svoju formulu.

Uređeni skup elemenata skupa naziva se raspored. Postavljanje se može ponavljati, odnosno jedan element se može koristiti više puta. I bez ponavljanja, kada se elementi ne ponavljaju. n su svi elementi, m su elementi koji učestvuju u postavljanju. Formula za postavljanje bez ponavljanja će izgledati ovako:

A n m =n!/(n-m)!

Veze od n elemenata koje se razlikuju samo po redosledu postavljanja nazivaju se permutacije. U matematici to izgleda ovako: P n = n!

Kombinacije od n elemenata od m su ona jedinjenja u kojima je bitno koji su elementi bili i koliki je njihov ukupan broj. Formula će izgledati ovako:

A n m =n!/m!(n-m)!

Bernulijeva formula

U teoriji vjerovatnoće, kao iu svakoj disciplini, postoje radovi izuzetnih istraživača u svojoj oblasti koji su je podigli na novi nivo. Jedan od ovih radova je Bernoullijeva formula, koja vam omogućava da odredite vjerovatnoću da će se određeni događaj dogoditi pod nezavisnim uvjetima. Ovo sugerira da pojava A u eksperimentu ne ovisi o pojavi ili nepostojanju istog događaja u ranijim ili kasnijim ispitivanjima.

Bernulijeva jednačina:

P n (m) = C n m ×p m ×q n-m.

Vjerovatnoća (p) pojave događaja (A) je konstantna za svako ispitivanje. Vjerovatnoća da će se situacija dogoditi tačno m puta u n broj eksperimenata izračunat će se prema gore prikazanoj formuli. Shodno tome, postavlja se pitanje kako saznati broj q.

Ako se događaj A dogodi p broj puta, prema tome, možda se neće dogoditi. Jedinica je broj koji se koristi za označavanje svih ishoda situacije u disciplini. Dakle, q je broj koji označava mogućnost da se događaj ne dogodi.

Sada znate Bernoullijevu formulu (teoriju vjerovatnoće). U nastavku ćemo razmotriti primjere rješavanja problema (prvi nivo).

Zadatak 2: Posjetilac trgovine će obaviti kupovinu sa vjerovatnoćom 0,2. 6 posetilaca je samostalno ušlo u radnju. Kolika je vjerovatnoća da će posjetitelj obaviti kupovinu?

Rješenje: Pošto je nepoznato koliko posjetitelja treba da izvrši kupovinu, jedan ili svih šest, potrebno je izračunati sve moguće vjerovatnoće koristeći Bernoullijevu formulu.

A = "posjetilac će izvršiti kupovinu."

U ovom slučaju: p = 0,2 (kako je navedeno u zadatku). Prema tome, q=1-0,2 = 0,8.

n = 6 (pošto u radnji ima 6 kupaca). Broj m će varirati od 0 (nijedan kupac neće izvršiti kupovinu) do 6 (svi posjetioci trgovine će nešto kupiti). Kao rezultat, dobijamo rješenje:

P 6 (0) = C 0 6 ×p 0 ×q 6 =q 6 = (0,8) 6 = 0,2621.

Nijedan od kupaca neće izvršiti kupovinu sa vjerovatnoćom 0,2621.

Kako se još koristi Bernoullijeva formula (teorija vjerovatnoće)? Primjeri rješavanja problema (drugi nivo) u nastavku.

Nakon gornjeg primjera, postavljaju se pitanja gdje su C i r otišli. U odnosu na p, broj na stepen od 0 će biti jednak jedan. Što se tiče C, može se naći po formuli:

C n m = n! /m!(n-m)!

Budući da je u prvom primjeru m = 0, respektivno, C = 1, što u principu ne utiče na rezultat. Koristeći novu formulu, pokušajmo saznati kolika je vjerovatnoća da dva posjetitelja kupe robu.

P 6 (2) = C 6 2 ×p 2 ×q 4 = (6×5×4×3×2×1) / (2×1×4×3×2×1) × (0,2) 2 × ( 0,8) 4 = 15 × 0,04 × 0,4096 = 0,246.

Teorija vjerovatnoće nije tako komplikovana. Bernoullijeva formula, čiji su primjeri prikazani gore, izravan je dokaz za to.

Poissonova formula

Poissonova jednačina se koristi za izračunavanje slučajnih situacija male vjerovatnoće.

osnovna formula:

P n (m)=λ m /m! × e (-λ) .

U ovom slučaju λ = n x p. Evo jednostavne Poissonove formule (teorija vjerovatnoće). U nastavku ćemo razmotriti primjere rješavanja problema.

Zadatak 3: Fabrika je proizvela 100.000 delova. Pojava neispravnog dijela = 0,0001. Kolika je vjerovatnoća da će u seriji biti 5 neispravnih dijelova?

Kao što vidite, brak je malo vjerojatan događaj i stoga se za izračunavanje koristi Poissonova formula (teorija vjerovatnoće). Primjeri rješavanja problema ove vrste se ne razlikuju od drugih zadataka u disciplini; potrebne podatke zamjenjujemo u datu formulu:

A = "slučajno odabrani dio će biti neispravan."

p = 0,0001 (prema uslovima zadatka).

n = 100000 (broj delova).

m = 5 (neispravni dijelovi). Zamjenjujemo podatke u formulu i dobivamo:

100000 R (5) = 10 5 /5! X e -10 = 0,0375.

Baš kao i Bernoullijeva formula (teorija vjerovatnoće), primjeri rješenja koje se koriste gore su napisani, Poissonova jednačina ima nepoznato e. U stvari, može se naći po formuli:

e -λ = lim n ->∞ (1-λ/n) n .

Međutim, postoje posebne tablice koje sadrže gotovo sve vrijednosti e.

De Moivre-Laplaceova teorema

Ako je u Bernoullijevoj shemi broj pokušaja dovoljno velik, a vjerovatnoća pojave događaja A u svim šemama ista, tada se vjerovatnoća pojave događaja A određeni broj puta u nizu testova može naći pomoću Laplaceova formula:

R n (m)= 1/√npq x ϕ(X m).

X m = m-np/√npq.

Da biste bolje zapamtili Laplaceovu formulu (teorija vjerojatnosti), primjeri problema su u nastavku koji će vam pomoći.

Prvo, pronađimo X m, zamijenimo podatke (svi su gore navedeni) u formulu i dobijemo 0,025. Pomoću tabela nalazimo broj ϕ(0,025), čija je vrijednost 0,3988. Sada možete zamijeniti sve podatke u formulu:

P 800 (267) = 1/√(800 x 1/3 x 2/3) x 0,3988 = 3/40 x 0,3988 = 0,03.

Dakle, vjerovatnoća da će letak raditi tačno 267 puta je 0,03.

Bayesova formula

Bayesova formula (teorija vjerojatnosti), primjeri rješavanja problema uz pomoć kojih će biti dati u nastavku, je jednadžba koja opisuje vjerovatnoću događaja na osnovu okolnosti koje bi mogle biti povezane s njim. Osnovna formula je sljedeća:

P (A|B) = P (B|A) x P (A) / P (B).

A i B su određeni događaji.

P(A|B) je uslovna vjerovatnoća, to jest, događaj A se može dogoditi pod uvjetom da je događaj B istinit.

P (B|A) - uslovna vjerovatnoća događaja B.

Dakle, završni dio kratkog kursa “Teorija vjerovatnoće” je Bayesova formula, primjeri rješenja problema s kojima su u nastavku.

Zadatak 5: U magacin su doneti telefoni tri firme. Istovremeno, udeo telefona koji se proizvodi u prvoj fabrici je 25%, u drugoj - 60%, u trećoj - 15%. Takođe je poznato da je prosečan procenat neispravnih proizvoda u prvoj fabrici 2%, u drugoj - 4%, au trećoj - 1%. Morate pronaći vjerovatnoću da će slučajno odabrani telefon biti neispravan.

A = "slučajno odabran telefon."

B 1 - telefon koji je proizvela prva fabrika. Shodno tome, pojavit će se uvodni B 2 i B 3 (za drugu i treću tvornicu).

Kao rezultat dobijamo:

P (B 1) = 25%/100% = 0,25; P(B 2) = 0,6; P (B 3) = 0,15 - tako smo pronašli vjerovatnoću svake opcije.

Sada morate pronaći uslovne vjerovatnoće željenog događaja, odnosno vjerovatnoću neispravnih proizvoda u kompanijama:

P (A/B 1) = 2%/100% = 0,02;

P(A/B 2) = 0,04;

P (A/B 3) = 0,01.

Sada zamenimo podatke u Bayesovu formulu i dobijemo:

P (A) = 0,25 x 0,2 + 0,6 x 0,4 + 0,15 x 0,01 = 0,0305.

Članak predstavlja teoriju vjerojatnosti, formule i primjere rješavanja problema, ali ovo je samo vrh ledenog brega jedne ogromne discipline. I nakon svega napisanog, logično će se postaviti pitanje da li je teorija vjerovatnoće potrebna u životu. Za običnog čoveka Teško je odgovoriti, bolje je pitati nekoga ko je to iskoristio za osvajanje džekpota više puta.
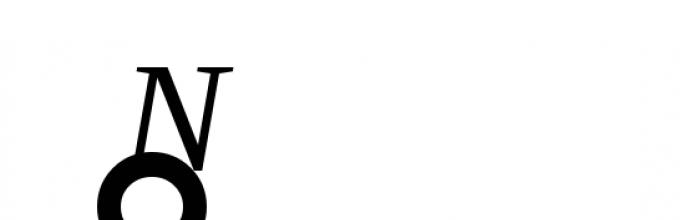