1. Sistemi linearne jednačine sa parametrom
Sistemi linearnih jednačina sa parametrom rešavaju se istim osnovnim metodama kao i obični sistemi jednačina: metodom zamene, metodom sabiranja jednačina i grafičkom metodom. Poznavanje grafičke interpretacije linearni sistemi olakšava odgovor na pitanje o broju korijena i njihovom postojanju.
Primjer 1.
Pronađite sve vrijednosti za parametar a za koji sistem jednačina nema rješenja.
(x + (a 2 – 3)y = a,
(x + y = 2.
Rješenje.
Pogledajmo nekoliko načina za rješavanje ovog zadatka.
1 način. Koristimo svojstvo: sistem nema rješenja ako je omjer koeficijenata ispred x jednak omjeru koeficijenata ispred y, ali nije jednak omjeru besplatni članovi(a/a 1 = b/b 1 ≠ c/c 1). tada imamo:
1/1 = (a 2 – 3)/1 ≠ a/2 ili sistem
(i 2 – 3 = 1,
(a ≠ 2.
Iz prve jednačine a 2 = 4, dakle, uzimajući u obzir uslov da je a ≠ 2, dobijamo odgovor.
Odgovor: a = -2.
Metoda 2. Rješavamo metodom zamjene.
(2 – y + (a 2 – 3)y = a,
(x = 2 – y,
((a 2 – 3)y – y = a – 2,
(x = 2 – y.
Nakon uzimanja zajedničkog faktora y iz zagrada u prvoj jednačini, dobijamo:
((a 2 – 4)y = a – 2,
(x = 2 – y.
Sistem nema rješenja ako prva jednačina nema rješenja, tj
(i 2 – 4 = 0,
(a – 2 ≠ 0.
Očigledno, a = ±2, ali uzimajući u obzir drugi uslov, odgovor dolazi samo sa odgovorom minus.
odgovor: a = -2.
Primjer 2.
Pronađite sve vrijednosti za parametar a za koji sistem jednadžbi ima beskonačan broj rješenja.
(8x + ay = 2,
(os + 2y = 1.
Rješenje.
Prema svojstvu, ako je omjer koeficijenata za x i y isti, i jednak je omjeru slobodnih članova sistema, onda on ima beskonačan broj rješenja (tj. a/a 1 = b/ b 1 = c/c 1). Stoga je 8/a = a/2 = 2/1. Rješavajući svaku od rezultirajućih jednačina, nalazimo da je a = 4 odgovor u ovom primjeru.
odgovor: a = 4.
2. Sistemi racionalne jednačine sa parametrom
Primjer 3.
(3|x| + y = 2,
(|x| + 2y = a.
Rješenje.
Pomnožimo prvu jednačinu sistema sa 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Oduzimanjem druge jednačine od prve, dobijamo 5|x| = 4 – a. Ova jednačina će imati jedina odluka za a = 4. U drugim slučajevima, ova jednačina će imati dva rješenja (za a< 4) или ни одного (при а > 4).
Odgovor: a = 4.
Primjer 4.
Pronađite sve vrijednosti parametra a za koje sistem jednadžbi ima jedinstveno rješenje.
(x + y = a,
(y – x 2 = 1.
Rješenje.
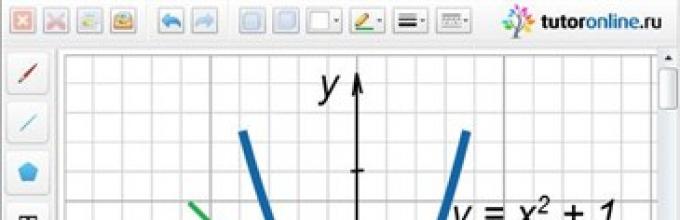
Ovaj sistem ćemo riješiti grafičkom metodom. Dakle, grafik druge jednačine sistema je parabola podignuta duž ose Oy nagore za jedan jedinični segment. Prva jednadžba specificira skup linija paralelnih pravoj y = -x (slika 1). Sa slike se jasno vidi da sistem ima rješenje ako je prava y = -x + a tangenta na parabolu u tački sa koordinatama (-0,5, 1,25). Zamjenom ovih koordinata u jednadžbu prave linije umjesto x i y, nalazimo vrijednost parametra a: 
1,25 = 0,5 + a;
Odgovor: a = 0,75.
Primjer 5.
Koristeći metodu zamjene, saznajte pri kojoj vrijednosti parametra a sistem ima jedinstveno rješenje.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Rješenje.
Iz prve jednačine izražavamo y i zamjenjujemo ga u drugu:
(y = ax – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.
Svodimo drugu jednačinu na oblik kx = b, koja će imati jedinstveno rješenje za k ≠ 0. Imamo:
ax + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
a 2 x + 3ax = 2 + a 2 + 3a + 2.
Kvadratni trinom a 2 + 3a + 2 predstavljamo kao proizvod zagrada
(a + 2)(a + 1), a na lijevoj strani vadimo x iz zagrada:
(a 2 + 3a)x = 2 + (a + 2)(a + 1).
Očigledno, a 2 + 3a ne bi trebalo da bude jednako nuli, dakle,
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, što znači a ≠ 0 i ≠ -3.
odgovor: a ≠ 0; ≠ -3.
Primjer 6.
Koristeći metodu grafičkog rješenja, odredite pri kojoj vrijednosti parametra a sistem ima jedinstveno rješenje.
(x 2 + y 2 = 9,
(y – |x| = a.
Rješenje.
Na osnovu uslova konstruišemo kružnicu sa centrom u početku i poluprečnikom od 3 jedinična segmenta; to je ono što je određeno prvom jednačinom sistema
x 2 + y 2 = 9. Druga jednačina sistema (y = |x| + a) je izlomljena linija. Korišćenjem slika 2 Razmatramo sve moguće slučajeve njegove lokacije u odnosu na krug. Lako je vidjeti da je a = 3. 
Odgovor: a = 3.
Imate još pitanja? Ne znate kako riješiti sisteme jednačina?
Da biste dobili pomoć od tutora, registrujte se.
Prva lekcija je besplatna!
web stranicu, kada kopirate materijal u cijelosti ili djelomično, link na izvor je obavezan.
Za koje vrijednosti parametra $a$ nejednakost $()-x^2 + (a + 2)x - 8a - 1 > 0$ ima barem jedno rješenje?
Rješenje
Smanjimo ovu nejednakost na pozitivan koeficijent za $x^2$:
$()-x^2 + (a + 2)x - 8a - 1 > 0 \quad \Leftrightarrow \quad x^2 - (a + 2)x + 8a + 1< 0 .$
Izračunajmo diskriminant: $D = (a + 2)^2 - 4(8a + 1) = a^2 + 4a + 4 - 32a - 4 = a^2 - 28a$. Da bi ova nejednakost imala rješenje, potrebno je da barem jedna tačka parabole leži ispod $x$ ose. Budući da su grane parabole usmjerene prema gore, to zahtijeva da kvadratni trinom na lijevoj strani nejednačine ima dva korijena, odnosno da njegov diskriminanta bude pozitivan. Dolazimo do potrebe da odlučimo kvadratna nejednakost$a^2 - 28a > 0$. Kvadratni trinom $a^2 - 28a$ ima dva korijena: $a_1 = 0$, $a_2 = 28$. Dakle, nejednakost $a^2 - 28a > 0$ je zadovoljena intervalima $a \in (-\infty; 0) \cup (28; + \infty)$.
Odgovori.$a \in (-\infty; 0) \cup (28; + \infty)$.
Za koje vrijednosti parametra $a$ jednačina $(a-2)x^2-2ax+a+3=0$ ima barem jedan korijen, a svi korijeni su pozitivni?
Rješenje
Neka je $a=2$. Tada jednačina poprima oblik $() - 4x +5 = 0$, iz čega dobijamo da je $x=\dfrac(5)(4)$ pozitivan korijen.
Neka sada $a\ne 2$. Ovo rezultira kvadratnom jednačinom. Prvo odredimo pri kojim vrijednostima parametra $a$ ova jednadžba ima korijen. Njegov diskriminant mora biti nenegativan. To je:
$ D = 4a^2 - 4(a-2)(a+3) =() -4a+24\geqslant 0\Leftrightarrow a\leqslant 6.$
Korijeni po uslovu moraju biti pozitivni, stoga iz Vietine teoreme dobijamo sistem:
$ \begin(cases)x_1 + x_2 = \dfrac(2a)(a - 2)>0,\\ x_1x_2 = \dfrac(a + 3)(a - 2)> 0,\\a\leqslant 6\end (slučajevi) \quad \Leftrightarrow \quad \begin(cases)a\in(- \infty;0)\cup(2; +\infty), \\ a\in(- \infty;-3)\cup( 2; +\infty), \\ a\in(-\infty;6] \end(cases)\quad\Leftrightarrow \quad a\in(-\infty;-3)\cup(2;6). $$
Kombinujemo odgovore i dobijamo traženi skup: $a\in(-\infty;-3)\cup$.
Odgovori.$a\in(-\infty;-3)\cup$.
Za koje vrijednosti parametra $a$ nejednakost $ax^2 + 4ax + 5 \leqslant 0$ nema rješenja?
Rješenje
- Ako je $a = 0$, onda se ova nejednakost degenerira u nejednakost $5 \leqslant 0$ , koja nema rješenja. Dakle, vrijednost $a = 0$ zadovoljava uslove problema.
- Ako je $a > 0$, onda graf kvadratni trinom na lijevoj strani nejednakosti nalazi se parabola sa granama usmjerenim prema gore. Izračunajmo $\dfrac(D)(4) = 4a^2 - 5a$. Nejednačina nema rješenja ako se parabola nalazi iznad x-ose, odnosno kada kvadratni trinom nema korijena ($D< 0$). Решим неравенство $4a^2 - 5a < 0$. Корнями квадратного трёхчлена $4a^2 - 5a$ являются числа $a_1 = 0$ и $a_2 = \dfrac{5}{4}$, поэтому $D < 0$ при $0 < a < \dfrac{5}{4}$. Значит, из pozitivne vrijednosti$a$ pogodni brojevi $a \in \levo(0; \dfrac(5)(4)\desno)$.
- Ako $a< 0$, то график квадратного трехчлена в левой части неравенства - парабола с ветвями, направленными вниз. Значит, обязательно найдутся значения $х$, для которых трёхчлен отрицателен. Следовательно, все значения $a < 0$ не подходят.
Odgovori.$a \in \left$ leži između korijena, tako da moraju postojati dva korijena (što znači $a\ne 0$). Ako su grane parabole $y = ax^2 + (a + 3)x - 3a$ usmjerene prema gore, tada je $y(-1)< 0$ и $y(1) < 0$; если же они направлены вниз, то $y(-1) >0$ i $y(1) > 0$.
Slučaj I. Neka je $a > 0$. Onda
$\left\( \begin(array)(l) y(-1)=a-(a+3)-3a=-3a-3<0 \\ y(1)=a+(a+3)-3a=-a+3<0 \\ a>0 \end(niz) \desno. \quad \Leftrightarrow \quad \left\( \begin(array)(l) a>-1 \\ a>3 \\ a>0 \end(array) \right.\quad \Leftrightarrow \quad a>3. $
To jest, u ovom slučaju ispada da su svi $a > 3$ prikladni.
Slučaj II. Neka $a< 0$. Тогда
$\left\( \begin(array)(l) y(-1)=a-(a+3)-3a=-3a-3>0 \\ y(1)=a+(a+3)-3a =-a+3>0 \\ a<0 \end{array} \right.\quad \Leftrightarrow \quad \left\{ \begin{array}{l} a<-1 \\ a<3 \\ a<0 \end{array} \right.\quad \Leftrightarrow \quad a<-1.$
To jest, u ovom slučaju ispada da su svi $a prikladni< -1$.
Odgovori.$a\in (-\infty ;-1)\cup (3;+\infty)$
Pronađite sve vrijednosti parametra $a$, za svaku od kojih postoji sistem jednadžbi
$ \begin(slučajevi) x^2+y^2 = 2a, \\ 2xy=2a-1 \end(slučajevi) $
ima tačno dva rješenja.
Rješenje
Oduzmite drugo od prvog: $(x-y)^2 = 1$. Onda
$ \left[\begin(niz)(l) x-y = 1, \\ x-y = -1 \end(niz)\desno. \quad \Leftrightarrow \quad \left[\begin(niz)(l) x = y+1, \\ x = y-1. \end(niz)\desno. $
Zamjenom rezultirajućih izraza u drugu jednačinu sistema, dobijamo dvije kvadratne jednačine: $2y^2 + 2y - 2a + 1 = 0$ i $2y^2 - 2y - 2a + 1 =0$. Diskriminanta svakog od njih je $D = 16a-4$.
Imajte na umu da se ne može dogoditi da par korijena prvog od kvadratne jednačine poklapa se s parom korijena druge kvadratne jednadžbe, jer je zbir korijena prve $-1$, a druge 1.
To znači da svaka od ovih jednačina mora imati jedan korijen, tada će originalni sistem imati dva rješenja. To jest, $D = 16a - 4 = 0$.
Odgovori.$a=\dfrac(1)(4)$
Pronađite sve vrijednosti parametra $a$ za svaku od kojih jednačina $4x-|3x-|x+a||=9|x-3|$ ima dva korijena.
Rješenje
Prepišimo jednačinu kao:
$ 9|x-3|-4x+|3x-|x+a|| = 0.$
Razmotrimo funkciju $f(x) = 9|x-3|-4x+|3x-|x+a||$.
Kada je $x\geqslant 3$ prvi modul se proširuje znakom plus, a funkcija ima oblik: $f(x) = 5x-27+|3x-|x+a||$. Očigledno je da će sa bilo kojim proširenjem modula rezultat biti linearna funkcija sa koeficijentom $k\geqslant 5-3-1=1>0$, odnosno ova funkcija raste beskonačno u datom intervalu.
Razmotrimo sada interval $x<3$. В этом случае первый модуль раскрывается с минусом, и функция принимает следующий вид: $f(x) = - 13x+27+|3x-|x+a||$. При любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом $k\leqslant - 13+3+1 = - 9<0$, то есть на этом промежутке функция убывает.
Dakle, dobili smo da je $x=3$ minimalna tačka ove funkcije. To znači da da bi originalna jednadžba imala dva rješenja, vrijednost funkcije u minimalnoj tački mora biti manja od nule. To jest, vrijedi sljedeća nejednakost: $f(3)<0$.
$ 12-|9-|3+a||>0 \quad \Leftrightarrow \quad |9-|3+a||< 12 \quad \Leftrightarrow \quad -12 < 9-|3+a| < 12 \quad \Leftrightarrow \quad$
$\Leftrightarrow\quad |3+a|< 21 \quad \Leftrightarrow \quad - 21 < 3+a < 21 \quad \Leftrightarrow \quad -24 Odgovori.$a \in (-24; 18)$ Za koje vrijednosti parametra $a$ jednačina $5^(2x)-3\cdot 5^x+a-1=0$ ima jedinstveni korijen? Napravimo zamjenu: $t = 5^x > 0$. Tada originalna jednačina poprima oblik kvadratne jednačine: $t^2-3t+a-1 =0$. Originalna jednadžba će imati jedan korijen ako ova jednačina ima jedan pozitivan korijen ili dva korijena, od kojih je jedan pozitivan, a drugi negativan. Diskriminanta jednačine je: $D = 13-4a$. Ova jednadžba će imati jedan korijen ako se ispostavi da je rezultirajući diskriminant jednak nuli, odnosno za $a = \dfrac(13)(4)$. U ovom slučaju, korijen $t=\dfrac(3)(2) > 0$, tako da je ova vrijednost $a$ prikladna. Ako postoje dva korijena, od kojih je jedan pozitivan, drugi nepozitivan, tada je $D = 13-4a > 0$, $x_1+x_2 = 3 > 0$ i $x_1x_2 = a - 1 \leqslant 0$ . To jest, $a\in(-\infty;1]$ Odgovori.$a\in(-\infty;1]\cup\left\(\dfrac(13)(4)\desno\)$ Pronađite sve vrijednosti parametra $a$ za koje je sistem $ \begin(slučajevi)\log_a y = (x^2-2x)^2, \\ x^2+y=2x\end(slučajevi) $ ima tačno dva rješenja. Hajde da transformišemo sistem u sledeći oblik: $ \begin(cases) \log_a y = (2x-x^2)^2, \\ y = 2x-x^2. \end(cases)$ Pošto je parametar $a$ u osnovi logaritma, na njega su nametnuta sljedeća ograničenja: $a>0$, $a \ne 1$. Pošto je varijabla $y$ argument logaritma, onda je $y > 0$. Nakon što smo spojili obje jednačine sistema, prelazimo na jednačinu: $\log_a y = y^2$. Ovisno o vrijednostima parametra $a$ moguća su dva slučaja: Odgovori.$a\in(0;1)$ Razmotrimo slučaj kada je $a > 1$. Budući da za velike apsolutne vrijednosti $t$ graf funkcije $f(t) = a^t$ leži iznad prave linije $g(t) = t$, tada jedina zajednička tačka može biti samo tačka tangentnosti. Neka je $t_0$ tačka dodira. U ovom trenutku, derivacija za $f(t) = a^t$ jednaka je jedinici (tangenta kuta tangente), osim toga, vrijednosti obje funkcije se poklapaju, odnosno sistem se odvija: $ \begin(slučajevi) a^(t_0)\ln a = 1, \\ a^(t_0) = t_0 \end(slučajevi) \quad \Leftrightarrow \quad \begin(slučajevi) a^(t_0) = \dfrac (1)(\ln a), \\ a^(\tau) = \tau \end(slučajevi) $ Otuda $t_0 = \dfrac(1)(\ln a)$. $ a^(\frac(1)(\ln a))\ln a = 1 \quad \Leftrightarrow \quad a^(\log_a e) =\frac(1)(\ln a) \quad \Leftrightarrow \quad a = e^(\frac(1)(e)). $ Istovremeno, drugi zajedničke tačke na pravoj liniji i eksponencijalna funkcija očigledno nije. Odgovori.$a \in (0;1] \cup \left\(e^(e^(-1))\desno\)$ Upotreba jednačina je široko rasprostranjena u našim životima. Koriste se u mnogim proračunima, izgradnji objekata, pa čak i u sportu. Čovjek je koristio jednačine u drevnim vremenima, a od tada se njihova upotreba samo povećava. U matematici postoje zadaci u kojima je potrebno tražiti rješenja za linearne i kvadratne jednadžbe u opšti pogled ili potražite broj korijena koje jednačina ima ovisno o vrijednosti parametra. Svi ovi zadaci imaju parametre. Razmotrite sljedeće jednačine kao ilustrativan primjer: \[y = kx,\] gdje su \ varijable, \ je parametar; \[y = kx + b,\] gdje su \ varijable, \ je parametar; \[ax^2 + bh + s = 0,\] gdje je \ varijabla, \[a, b, s\] je parametar. Rješavanje jednadžbe sa parametrom znači, po pravilu, rješavanje beskonačnog skupa jednačina. Međutim, slijedeći određeni algoritam, lako možete riješiti sljedeće jednadžbe: 1. Odredite “kontrolne” vrijednosti parametra. 2. Riješite originalnu jednačinu za [\x\] sa vrijednostima parametara definiranim u prvom paragrafu. 3. Riješite originalnu jednačinu za [\x\] za vrijednosti parametara različite od onih odabranih u prvom paragrafu. Recimo da nam je data sljedeća jednačina: \[\mid 6 - x \mid = a.\] Nakon analize početnih podataka, jasno je da je \[\ge 0.\] Prema pravilu modula \ izražavamo \ Odgovor: \gdje\ Jednačinu možete riješiti na našoj web stranici https://site. Besplatni online rješavač će vam omogućiti da riješite online jednadžbe bilo koje složenosti za nekoliko sekundi. Sve što trebate učiniti je jednostavno unijeti svoje podatke u rješavač. Također možete pogledati video upute i naučiti kako riješiti jednadžbu na našoj web stranici. A ako i dalje imate pitanja, možete ih postaviti u našoj VKontakte grupi http://vk.com/pocketteacher. Pridružite se našoj grupi, mi ćemo vam uvijek rado pomoći.Rješenje
Rješenje
Gdje mogu riješiti jednačinu s parametrom na mreži?