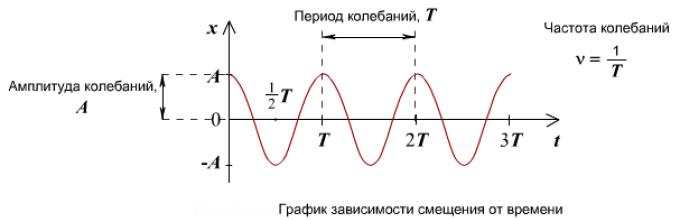
Jednačina harmonijskih vibracija
Jednačina harmonijskog oscilovanja utvrđuje zavisnost koordinata tela o vremenu
Kosinusni graf u početnom trenutku ima maksimalnu vrijednost, a sinusni graf ima nultu vrijednost u početnom trenutku. Ako oscilaciju počnemo ispitivati iz ravnotežnog položaja, tada će oscilacija ponoviti sinusoidu. Ako oscilaciju počnemo razmatrati s pozicije maksimalnog odstupanja, tada će oscilacija biti opisana kosinusom. Ili se takva oscilacija može opisati sinusnom formulom sa početnom fazom.
Promjena brzine i ubrzanja tokom harmonijskih oscilacija
Ne samo da se koordinate tijela mijenjaju tokom vremena prema zakonu sinusa ili kosinusa. Ali veličine kao što su sila, brzina i ubrzanje također se mijenjaju na sličan način. Sila i ubrzanje su maksimalne kada je oscilirajuće tijelo na krajnjim pozicijama gdje je pomak maksimalan, a nula kada tijelo prolazi kroz ravnotežni položaj. Brzina je, naprotiv, u ekstremnim položajima nula, a kada tijelo prođe kroz ravnotežni položaj, ono dostiže svoju maksimalnu vrijednost.
Ako je oscilacija opisana zakonom kosinusa
Ako je oscilacija opisana prema sinusnom zakonu
Maksimalne vrijednosti brzine i ubrzanja
Analizirajući jednadžbe zavisnosti v(t) i a(t), možemo pretpostaviti da maksimalne vrijednosti brzine i ubrzanja poprimaju slučaj kada trigonometrijski faktor jednako 1 ili -1. Određeno formulom
Harmonične vibracije su vibracije u kojima fizička količina mijenja se tokom vremena prema harmonijskom (sinusoidnom, kosinusnom) zakonu. Jednačina harmonijske vibracije može se napisati na sljedeći način:
X(t) = A∙cos(ω t+φ )
ili
X(t) = A∙sin(ω t+φ)
X - odstupanje od ravnotežnog položaja u trenutku t
A - amplituda vibracije, dimenzija A se poklapa sa dimenzijom X
ω - ciklička frekvencija, rad/s (radijani po sekundi)
φ - početna faza, rad
t - vrijeme, s
T - period oscilovanja, s
f - frekvencija oscilacije, Hz (Hertz)
π je konstanta približno jednaka 3,14, 2π=6,28
Period oscilovanja, frekvencija u hercima i ciklička frekvencija povezani su relacijama.
ω=2πf , T=2π/ω , f=1/T , f=ω/2π
Da biste zapamtili ove odnose, morate razumjeti sljedeće.
Svaki od parametara ω, f, T jednoznačno određuje ostale. Za opis oscilacija dovoljno je koristiti jedan od ovih parametara.
Period T je vrijeme jedne oscilacije, pogodno je koristiti za crtanje grafika oscilacija.
Ciklična frekvencija ω - koristi se za pisanje jednačina oscilacija, omogućava matematičke proračune.
Frekvencija f je broj oscilacija u jedinici vremena, svuda korištenih. U hercima mjerimo frekvenciju na koju su radio uređaji podešeni, kao i radni domet mobilnih telefona. Učestalost vibracija žica prilikom podešavanja muzičkih instrumenata mjeri se u hercima.
Izraz (ωt+φ) naziva se faza oscilovanja, a vrijednost φ se naziva početna faza, jer je jednaka fazi oscilovanja u trenutku t=0.
Funkcije sinusa i kosinusa opisuju omjer strana u pravougaonog trougla. Stoga mnogi ne razumiju kako su ove funkcije povezane s harmonijskim vibracijama. Ovaj odnos je prikazan jednoliko rotirajućim vektorom. Projekcija jednoliko rotirajućeg vektora vrši harmonijske oscilacije.
Na slici ispod prikazan je primjer tri harmonijske vibracije. Jednake frekvencije, ali različite faze i amplitude. 
Nekoliko smo ih fizički pogledali u potpunosti razni sistemi, i pobrinuo se da se jednačine kretanja svedu na isti oblik
Razlika između fizički sistemi pojavljuju se samo u drugačija definicija količine i u raznim fizičkog čula varijabla x: to može biti koordinata, ugao, naelektrisanje, struja itd. Imajte na umu da u ovom slučaju, kao što sledi iz same strukture jednačine (1.18), veličina uvek ima dimenziju inverznog vremena.
Jednačina (1.18) opisuje tzv harmonijske vibracije.
Jednačina harmonijskih vibracija (1.18) je linearna diferencijalna jednadžba drugog reda (pošto sadrži drugi izvod varijable x). Linearnost jednačine to znači
ako neka funkcija x(t) je rješenje ove jednadžbe, onda funkcija Cx(t)će također biti njegovo rješenje ( C– proizvoljna konstanta);
if funkcije x 1 (t) I x 2(t) su rješenja ove jednadžbe, zatim njihov zbir x 1 (t) + x 2 (t) također će biti rješenje iste jednačine.
To je također dokazano matematička teorema, prema kojem jednačina drugog reda ima dva nezavisna rješenja. Sva ostala rješenja, prema svojstvima linearnosti, mogu se dobiti kao njihove linearne kombinacije. Lako je direktnom diferencijacijom provjeriti da nezavisne funkcije i zadovoljavaju jednačinu (1.18). znači, zajednička odluka ova jednačina izgleda ovako:
Gdje C 1,C 2- proizvoljne konstante. Ovo rješenje se može predstaviti u drugom obliku. Unesite vrijednost
|
|
i odredimo ugao relacijama:
|
|
Tada se opće rješenje (1.19) zapisuje kao
Prema trigonometrijskim formulama, izraz u zagradama je jednak
Konačno dolazimo k sebi opšte rješenje jednačine harmonijskih vibracija kao:
Nenegativna vrijednost A pozvao amplituda vibracije, - početna faza oscilovanja. Poziva se cijeli kosinusni argument - kombinacija faza oscilovanja.
Izrazi (1.19) i (1.23) su potpuno ekvivalentni, tako da možemo koristiti bilo koji od njih, na osnovu razmatranja jednostavnosti. Oba rješenja jesu periodične funkcije vrijeme. Zaista, sinus i kosinus su periodični sa periodom . Stoga se različita stanja sistema koji vrši harmonijske oscilacije ponavljaju nakon određenog vremenskog perioda t*, tokom koje faza oscilovanja dobija povećanje koje je višestruko od :
Iz toga slijedi
Najmanje ovih vremena
pozvao period oscilovanja (Sl. 1.8), i - njegov kružni (ciklički) frekvencija.
Rice. 1.8.
Takođe koriste frekvencija fluktuacije
|
|
Prema tome, kružna frekvencija je jednaka broju oscilacija po sekundi
Dakle, ako je sistem na vrijeme t karakterizirana vrijednošću varijable x(t), tada će varijabla imati istu vrijednost nakon određenog vremenskog perioda (slika 1.9), tj
Isto značenje će se prirodno ponavljati tokom vremena 2T, ZT itd.
Rice. 1.9. Period oscilovanja
Opće rješenje uključuje dvije proizvoljne konstante ( C 1, C 2 ili A, a), čije vrijednosti moraju biti određene sa dva početni uslovi. Obično (iako ne nužno) njihovu ulogu igraju početne vrijednosti varijable x(0) i njen derivat.
Dajemo primjer. Neka rješenje (1.19) jednadžbe harmonijskih oscilacija opisuje kretanje opružnog klatna. Vrijednosti proizvoljnih konstanti zavise od načina na koji smo klatno izveli iz ravnoteže. Na primjer, povukli smo oprugu na daljinu i pustio loptu bez početne brzine. U ovom slučaju
Zamena t = 0 u (1.19) nalazimo vrijednost konstante C 2
Rešenje tako izgleda:
Brzinu opterećenja nalazimo diferenciranjem u odnosu na vrijeme
Zamena ovde t = 0, pronađite konstantu C 1:
Konačno
Upoređujući sa (1.23), nalazimo da je amplituda oscilacija, a njena početna faza je nula: .
Hajde da sada izbalansiramo klatno na drugi način. Udarimo teret tako da dobije početnu brzinu, ali se praktički ne pomiče tokom udara. Tada imamo druge početne uslove:
naše rešenje izgleda tako
Brzina tereta će se mijenjati prema zakonu:
Zamijenimo ovdje:
Promjene u bilo kojoj količini opisuju se korištenjem zakona sinusa ili kosinusa, tada se takve oscilacije nazivaju harmonijskim. Razmotrimo kolo koje se sastoji od kondenzatora (koji je bio napunjen prije uključivanja u kolo) i induktora (slika 1).
Slika 1.
Jednačina harmonijske vibracije može se napisati na sljedeći način:
$q=q_0cos((\omega )_0t+(\alpha )_0)$ (1)
gdje je $t$ vrijeme; $q$ naknada, $q_0$-- maksimalno odstupanje naboja od njegove prosječne (nulte) vrijednosti tokom promjena; $(\omega )_0t+(\alpha )_0$- faza oscilacije; $(\alpha )_0$- početna faza; $(\omega )_0$ - ciklična frekvencija. Tokom perioda, faza se mijenja za $2\pi $.
Jednadžba oblika:
jednadžba harmonijskih oscilacija u diferencijalnom obliku za oscilatorno kolo koje neće sadržavati aktivni otpor.
Bilo koja vrsta periodičnih oscilacija može se tačno predstaviti kao zbir harmonijskih oscilacija, takozvani harmonijski niz.
Za period oscilovanja kola koje se sastoji od zavojnice i kondenzatora, dobijamo Thomsonovu formulu:
Ako razlikujemo izraz (1) s obzirom na vrijeme, možemo dobiti formulu za funkciju $I(t)$:
Napon na kondenzatoru se može naći kao:
Iz formula (5) i (6) proizilazi da je jačina struje ispred napona na kondenzatoru za $\frac(\pi )(2).$
Harmonične oscilacije se mogu predstaviti i u obliku jednačina, funkcija i vektorskih dijagrama.
Jednačina (1) predstavlja slobodne neprigušene oscilacije.
Jednačina prigušenih oscilacija
Promjena naboja ($q$) na pločama kondenzatora u kolu, uzimajući u obzir otpor (slika 2), biće opisana diferencijalnom jednačinom oblika:
Slika 2.
Ako je otpor koji je dio kola $R\
gdje je $\omega =\sqrt(\frac(1)(LC)-\frac(R^2)(4L^2))$ frekvencija ciklične oscilacije. $\beta =\frac(R)(2L)-$koeficijent prigušenja. Amplituda prigušenih oscilacija izražava se kao:
Ako je pri $t=0$ naboj na kondenzatoru jednak $q=q_0$ i nema struje u kolu, tada za $A_0$ možemo napisati:
Faza oscilacija u početnom trenutku vremena ($(\alpha )_0$) je jednaka:
Kada $R >2\sqrt(\frac(L)(C))$ promjena naboja nije oscilacija, pražnjenje kondenzatora se naziva aperiodično.
Primjer 1
vježba: Maksimalna vrijednost naplate je $q_0=10\ C$. Harmonično varira sa periodom od $T= 5 s$. Odredite maksimalnu moguću struju.
Rješenje:
Kao osnovu za rješavanje problema koristimo:
Da bismo pronašli jačinu struje, izraz (1.1) se mora razlikovati s obzirom na vrijeme:
gdje je maksimum (vrijednost amplitude) jačine struje izraz:
Iz uslova zadatka znamo amplitudnu vrijednost naboja ($q_0=10\ C$). Trebali biste pronaći prirodnu frekvenciju oscilacija. Izrazimo to kao:
\[(\omega )_0=\frac(2\pi )(T)\left(1.4\desno).\]
U ovom slučaju, željena vrijednost će se naći pomoću jednačina (1.3) i (1.2) kao:
Pošto su sve veličine u uslovima problema prikazane u SI sistemu, izvršićemo proračune:
odgovor:$I_0=12,56\ A.$
Primjer 2
vježba: Koliki je period oscilovanja u kolu koje sadrži induktor $L=1$H i kondenzator, ako se jačina struje u kolu mijenja prema zakonu: $I\left(t\right)=-0.1sin20\ pi t\ \left(A \right)?$ Koliki je kapacitet kondenzatora?
Rješenje:
Iz jednadžbe strujnih fluktuacija, koja je data u uslovima zadatka:
vidimo da je $(\omega )_0=20\pi $, stoga možemo izračunati period oscilacije koristeći formulu:
\ \
Prema Thomsonovoj formuli za kolo koje sadrži induktor i kondenzator, imamo:
Izračunajmo kapacitet:
odgovor:$T=0.1$ c, $C=2.5\cdot (10)^(-4)F.$
§ 6. MEHANIČKE VIBRACIJEOsnovne formule
Harmonic Equation
Gdje X - pomicanje oscilirajuće tačke iz ravnotežnog položaja; t- vrijeme; A,ω, φ - amplituda, ugaona frekvencija, početna faza oscilacija, respektivno; - faza oscilacija u ovom trenutku t.
Ugaona frekvencija
gdje su ν i T frekvencija i period oscilacija.
Brzina tačke koja vrši harmonijske oscilacije je
Ubrzanje tokom harmonijskih oscilacija
Amplituda A rezultujuća oscilacija dobijena zbrajanjem dve oscilacije sa istim frekvencijama, koje se javljaju duž jedne prave linije, određena je formulom
Gdje a 1 I A 2 - amplitude vibracijskih komponenti; φ 1 i φ 2 su njihove početne faze.
Početna faza φ rezultirajuće oscilacije može se naći iz formule
Frekvencija otkucaja koja nastaje pri sabiranju dvije oscilacije koje se javljaju duž jedne prave linije s različitim, ali sličnim frekvencijama ν 1 i ν 2,
Jednadžba putanje tačke koja učestvuje u dvije međusobno okomite oscilacije sa amplitudama A 1 i A 2 i početnim fazama φ 1 i φ 2,
Ako su početne faze φ 1 i φ 2 komponenti oscilovanja iste, tada jednačina putanje ima oblik
odnosno tačka se kreće pravolinijski.
U slučaju da je fazna razlika , jednačina poprima oblik
odnosno tačka se kreće duž elipse.
Diferencijalna jednadžba harmonijskih oscilacija materijalne tačke
, ili 
, gdje je m masa tačke; k-
koeficijent kvazielastične sile ( k=Tω 2).
Ukupna energija materijalne tačke koja vrši harmonijske oscilacije je
Period oscilovanja tela okačenog na oprugu (opružno klatno)
Gdje m- tjelesna masa; k- krutost opruge. Formula vrijedi za elastične vibracije u granicama u kojima je zadovoljen Hookeov zakon (sa malom masom opruge u odnosu na masu tijela).
Period oscilovanja matematičkog klatna
Gdje l- dužina klatna; g- ubrzanje gravitacije. Period oscilovanja fizičkog klatna
Gdje J- moment inercije oscilirajućeg tijela u odnosu na osu
oklijevanje; A- udaljenost centra mase klatna od ose oscilovanja;
Smanjena dužina fizičkog klatna.
Date formule su tačne za slučaj infinitezimalnih amplituda. Za konačne amplitude ove formule daju samo približne rezultate. Sa amplitudama ne većim od, greška u vrijednosti perioda ne prelazi 1%.
Period torzionih vibracija tijela okačenog na elastični navoj je
Gdje J- moment inercije tijela u odnosu na osu koja se poklapa s elastičnim navojem; k- elastična krutost niti, jednak omjeru moment elastičnosti koji nastaje kada se konac uvija, do ugla pod kojim je konac uvrnut.
Diferencijalna jednadžba prigušenih oscilacija 
, ili ,
Gdje r- koeficijent otpora; δ - koeficijent prigušenja: ;ω 0 - prirodna ugaona frekvencija oscilacija *
Jednačina prigušenih oscilacija
Gdje A(t)- amplituda prigušenih oscilacija u ovom trenutku t;ω je njihova ugaona frekvencija.
Ugaona frekvencija prigušenih oscilacija
O Zavisnost amplitude prigušenih oscilacija od vremena
I
Gdje A 0 - amplituda oscilacija u trenutku t=0.
Dekrement logaritamskih oscilacija
Gdje A(t) I A(t+T)- amplitude dvije uzastopne oscilacije razdvojene u vremenu periodom.
Diferencijalna jednadžba prisilnih oscilacija
gdje je vanjska periodična sila koja djeluje na oscilirajuću materijalnu tačku i uzrokuje prisilne oscilacije; F 0 - vrijednost njegove amplitude;
Amplituda prisilnih oscilacija
Rezonantna frekvencija i rezonantna amplituda 
I
Primjeri rješavanja problema
Primjer 1. Tačka oscilira po zakonu x(t)=
,
Gdje A=2 vidi Odrediti početnu fazu φ if
x(0)=cm i X , (0)<0. Построить векторную диаграмму для мо- мента t=0.
Rješenje. t Koristimo jednačinu kretanja i izrazimo pomak u ovom trenutku
=0 kroz početnu fazu:
Odavde nalazimo početnu fazu:
* U prethodno datim formulama za harmonijske vibracije, ista veličina je označena jednostavno ω (bez indeksa 0). x Zamijenimo date vrijednosti u ovaj izraz (0) iφ=
= 
O:
. Vrijednost argumenta je zadovoljena sa dvije vrijednosti ugla:
Da bismo odlučili koja od ovih vrijednosti ugla φ također zadovoljava uvjet, prvo nalazimo: t Zamjena vrijednosti u ovaj izraz
=0 i naizmjenično vrijednosti početnih faza i, nalazimo 
T A>0 i ω>0, tada samo prva vrijednost početne faze zadovoljava uvjet. Dakle, željena početna faza
Koristeći pronađenu vrijednost φ, konstruiramo vektorski dijagram (slika 6.1). Primjer 2. Materijalna tačka sa masom T=5 g vrši harmonijske oscilacije sa frekvencijom ν =0,5 Hz. Amplituda oscilacije A=3 cm Odrediti: 1) brzinu υ tačke u trenutku kada je pomak x== 1,5 cm; 2) maksimalna sila F max koja deluje na tačku; 3) Fig. 6.1 ukupna energija E oscilirajuća tačka.
i dobijamo formulu brzine uzimajući prvi vremenski izvod pomaka:
Za izražavanje brzine kroz pomak, potrebno je isključiti vrijeme iz formula (1) i (2). Da bismo to učinili, kvadriramo obje jednadžbe i prvu podijelimo sa A 2 , drugi na A 2 ω 2 i dodajte:
, ili 
Nakon što smo riješili posljednju jednačinu za υ , naći ćemo
Nakon što smo izvršili proračune koristeći ovu formulu, dobijamo
Znak plus odgovara slučaju kada se smjer brzine poklapa s pozitivnim smjerom ose X, znak minus - kada se smjer brzine poklapa sa negativnim smjerom ose X.
Pomak za vrijeme harmonijske oscilacije, pored jednačine (1), može se odrediti i jednačinom
Ponavljajući isto rješenje sa ovom jednačinom, dobijamo isti odgovor.
2. Pronalazimo silu koja djeluje na tačku koristeći Newtonov drugi zakon:
Gdje A - ubrzanje tačke, koje dobijamo uzimanjem vremenskog izvoda brzine:
Zamjenom izraza ubrzanja u formulu (3) dobijamo
Otuda i maksimalna vrijednost sile
Zamjenom vrijednosti π, ν u ovu jednačinu, T I A, naći ćemo
3. Ukupna energija oscilirajuće tačke je zbir kinetičke i potencijalne energije izračunate za bilo koji trenutak u vremenu.
Najlakši način da se izračuna ukupna energija je u trenutku kada kinetička energija dostigne svoju maksimalnu vrijednost. U ovom trenutku potencijalna energija je nula. Dakle, ukupna energija E oscilirajuća tačka je jednaka maksimalnoj kinetičkoj energiji
Maksimalnu brzinu određujemo iz formule (2), stavljajući: 
. Zamjenom izraza za brzinu u formulu (4) nalazimo
Zamjenom vrijednosti količina u ovu formulu i izračunima, dobijamo
ili µJ.
Primjer 3. Na krajevima dužine tanke šipke l= 1 m i masa m 3 =400 g ojačane male kuglice sa masama m 1 =200 g I m 2 =300g. Štap oscilira oko horizontalne ose, okomito
u odnosu na štap i prolazi kroz njegovu sredinu (tačka O na slici 6.2). Definišite period T oscilacije koje vrši štap.
Rješenje.
Period oscilovanja fizičkog klatna, kao što je štap sa kuglicama, određen je relacijom J- Gdje T - l njegova masa; - udaljenost od centra mase klatna do ose.
Moment inercije ovog klatna jednak je zbiru momenata inercije kuglica J 1 i J 2 i štap J 3:
Uzimanje lopte za materijalne tačke, izrazimo njihove momente inercije:
Budući da os prolazi kroz sredinu štapa, njen moment inercije u odnosu na ovu osu J 3 = =. Zamjena rezultirajućih izraza J 1 , J 2 I J 3 u formulu (2), nalazimo opšti trenutak inercija fizičkog klatna:
Provodeći proračune koristeći ovu formulu, nalazimo
Rice. 6.2 Masu klatna čine mase kuglica i masa štapa:
Razdaljina l njegova masa; Naći ćemo centar mase klatna iz ose oscilovanja na osnovu sljedećih razmatranja. Ako je os X usmjeriti duž štapa i poravnati početak koordinata sa tačkom O, zatim traženu udaljenost l jednak koordinati centra mase klatna, tj.
Zamjena vrijednosti količina m 1 , m 2 , m, l i nakon proračuna nalazimo
Nakon što smo izvršili proračune koristeći formulu (1), dobijamo period oscilovanja fizičkog klatna:
Primjer 4. Fizičko klatno je štap dužine l= 1 m i masa 3 T 1 With pričvršćen na jedan od njegovih krajeva obručem prečnika i mase T 1 . Horizontalna os Oz
klatno prolazi kroz sredinu štapa okomito na njega (slika 6.3). Definišite period T oscilacije takvog klatna.
Rješenje.
(1)
Gdje J- Period oscilovanja fizičkog klatna određuje se formulom Gdje T - l moment inercije klatna u odnosu na osu oscilovanja; - C
udaljenost od centra mase klatna do ose oscilovanja. J 1 Moment inercije klatna jednak je zbiru momenata inercije štapa J 2:
(2).
i obruč 
Moment inercije štapa u odnosu na osu okomitu na štap i koja prolazi kroz njegovo središte mase određuje se formulom . U ovom slučaju 3T t=
1 i 
Moment inercije obruča nalazimo koristeći Steinerov teorem J-
,Gdje J 0
-
moment inercije oko proizvoljne ose; A - moment inercije oko ose koja prolazi kroz centar mase paralelno datoj osi;
razmak između naznačenih osa. Primjenjujući ovu formulu na obruč, dobivamo J Zamjenjivanje izraza J 1 i
Razdaljina l njegova masa; 2 u formulu (2), nalazimo moment inercije klatna u odnosu na os rotacije:
od ose klatna do njegovog centra mase je jednako J, l Zamjena izraza u formulu (1)
s i masu klatna, nalazimo period njegovih oscilacija: Nakon izračunavanja pomoću ove formule dobijamo T
=2,17 s. Primjer 5. X 2 = Sabiraju se dvije oscilacije istog smjera, izražene jednadžbama; A 1 = 1 =, gdje A cm,
2 =2 cm, s, s, ω = =. 1. Odrediti početne faze φ 1 i φ 2 komponenti oscilatora A Baniya. 2. Pronađite amplitudu
i početna faza φ rezultirajuće oscilacije. Napišite jednačinu za rezultirajuću vibraciju.
Transformirajmo jednadžbe navedene u iskazu problema u isti oblik:
Iz poređenja izraza (2) sa jednakošću (1) nalazimo početnu fazu prve i druge oscilacije:
Drago mi je i 
drago.
2. Odrediti amplitudu A rezultujuće oscilacije, zgodno je koristiti vektorski dijagram predstavljen u pirinač. 6.4. Prema kosinusnoj teoremi, dobijamo
gdje je fazna razlika komponenti oscilovanja 
, tada zamjenom pronađenih vrijednosti φ 2 i φ 1 dobijamo rad.
Zamenimo vrednosti A 1 , A 2 i u formulu (3) i izvršite proračune:
A= 2,65 cm.
Odredimo tangentu početne faze φ rezultujuće oscilacije direktno sa Sl. 6.4: 
, odakle dolazi početna faza?
