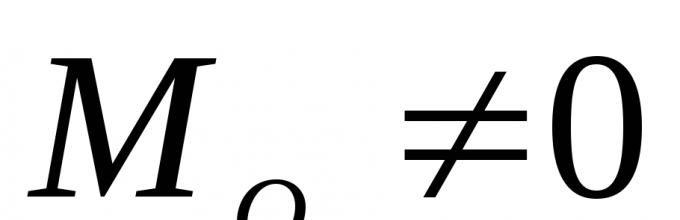Ravni sistem proizvoljno lociranih sila.

Uslovi za ravnotežu parova sila.

Ako na čvrsto tijelo djeluje nekoliko parova sila, proizvoljno lociranih u prostoru, onda se uzastopnom primjenom pravila paralelograma na svaka dva momenta parova sila, bilo koji broj parova sila može zamijeniti jednim ekvivalentnim parom sila. , čiji je moment jednak zbiru momenata datih parova sila.

Teorema. Za ravnotežu parova sila primijenjenih na čvrsto tijelo, potrebno je i dovoljno da algebarski zbir projekcija momenata parova sila na svaku od tri koordinatne ose bude jednak nuli.

Razmotrimo slučaj prijenosa sile na proizvoljnu tačku koja ne leži na liniji djelovanja sile.

Uzmimo silu F primijenjenu u tački C. Ovu silu paralelno sa sobom trebamo prenijeti u određenu tačku O. Primijenimo u tački O dvije sile F" i F", suprotno usmjerene, jednake vrijednosti i paralelne sa datom sila F, tj. F" = F" = F. Primjena ovih sila u tački O ne mijenja stanje tijela, jer su one međusobno uravnotežene. Rezultirajući sistem od tri sile se može smatrati da se sastoji od sile F" primijenjene u tački O i para sila FF" sa momentom M = Fa. Ovaj par sila se zove pripojen, a njegov krak a je jednak kraku sile F u odnosu na tačku O.

Dakle, kada se sila F dovede u tačku koja ne leži na liniji djelovanja sile, dobija se ekvivalentni sistem koji se sastoji od sile iste veličine i smjera kao i sila F i vezanog para sila, čiji je moment jednak momentu date sile u odnosu na bačenu tačku:

Kao primjer smanjenja sile razmotrite djelovanje sile F na kraj C stegnute šipke (slika 28, b). Nakon što smo silu F doveli u tačku O stegnutog presjeka, u njoj nalazimo silu F1 jednaku i paralelnu datoj, i pridruženi moment M jednak momentu date sile F u odnosu na tačku redukcije O,

1.4.2 Dovođenje ravan sistema sila u datu tačku

Opisani metod dovođenja jedne sile u datu tačku može se primijeniti na bilo koji broj sila. Pretpostavimo da su sile F1, F2, F3, F4 primijenjene u tačkama tijela A, B, C i D (slika 30).

Potrebno je dovesti ove sile u tačku O ravni. Predstavimo prvo silu F1 primijenjenu u tački A. Primijenimo na tačku O dvije sile F1" i F1"", paralelne sa njom i usmjerene u suprotnim smjerovima. Kao rezultat dovođenja sile F1, dobijamo primijenjenu silu F1" u tački O, i par sila F1 "F1" sa ramenom a1. Isto tako sa silom F2 primijenjenom u tački B, dobijamo silu F2" primijenjenu u tački O, i par sila sa ramenom a2 itd.

Zamenili smo ravan sistem sila primenjenih u tačkama A, B, C i D sa konvergentnim silama F1, F2, F3, F4 primenjenim u tački O, a parove sila sa momentima jednakim momentima datih sila u odnosu na tačku O. :



Sile koje konvergiraju u tački mogu se zamijeniti jednom silom F"hl, jednakom geometrijskom zbiru komponenti,

Ova sila, jednaka geometrijskom zbiru datih sila, naziva se glavni vektor sistema sila i označavaju F"ch.

Na osnovu pravila za sabiranje parova sila, one se mogu zamijeniti rezultirajućim parom, čiji je moment jednak algebarskom zbiru momenata datih sila u odnosu na tačku O i naziva se glavna tačka u odnosu na referentnu tačku

Shodno tome, u opštem slučaju, ravan sistem sila kao rezultat redukcije na datu tačku O je zamenjen ekvivalentnim sistemom koji se sastoji od jedne sile (glavni vektor) i jednog para (glavni moment).

Potrebno je shvatiti da je glavni vektor F"ch rezultanta datog sistema sila, jer ovaj sistem nije ekvivalentan jednoj sili F"ch. Samo u posebnom slučaju kada glavni moment nestane bit će glavni vektor rezultanta datog sistema sila. Pošto je glavni vektor jednak geometrijskom zbiru sila datog sistema, ni njegova veličina ni njegov pravac ne zavise od izbora centra redukcije. Vrijednost i predznak glavnog momenta Mgl zavise od položaja centra redukcije, budući da krakovi parova komponenti zavise od relativnog položaja sila i tačke (centra) u odnosu na koju se momenti uzimaju.

Mogu se javiti sljedeći slučajevi dovođenja sistema snaga:
1. - opšti slučaj; sistem se svodi na glavni vektor i na glavni momenat.
2. ; sistem se svodi na jednu rezultantu jednaku glavnom vektoru sistema.
3. ; sistem se svodi na par sila čiji je moment jednak glavnom momentu.
4. ; sistem je u ravnoteži, odnosno za ravnotežu ravnog sistema sila potrebno je i dovoljno da njegov glavni vektor i glavni moment budu istovremeno jednaki nuli.

Može se dokazati da u opštem slučaju, kada, uvek postoji tačka oko koje je glavni moment sila jednak nuli.

Razmotrimo ravan sistem sila koji je doveden u tačku O, odnosno zamijenjen glavnim vektorom primijenjenim u tački O i glavnim momentom. Radi određenosti, pretpostavljamo da je glavni moment usmjeren u smjeru kazaljke na satu, tj. Predstavimo ovaj glavni moment kao par sila FF", čiji će modul biti izabran jednak modulu glavnog vektora, tj. primijenit ćemo jednu od sila koje čine par u centru redukcije O, druga sila u tački C čiji će se položaj odrediti iz uslova: Prema tome .

Postavimo par sila tako da sila F"" bude usmjerena u smjeru suprotnom od glavnog vektora F"ch. U tački O imamo dvije jednake međusobno suprotne sile F"ch i F"", usmjerene duž iste prave linija; mogu se odbaciti (prema trećem aksiomu). Prema tome, u odnosu na tačku C, glavni moment sistema sila koji se razmatra jednak je nuli, a sistem se svodi na rezultantu.

Dovođenje sistema snaga u centar

Pitanja

Predavanje 6

3. Uslovi ravnoteže za proizvoljni sistem sila

1. Razmotrimo proizvoljan sistem sila. Odaberimo proizvoljnu tačku O iza centra redukcije i, koristeći teoremu o paralelnom prenosu sile, prenosimo sve sile sistema u datu tačku, ne zaboravljajući da pri prenošenju svake sile dodamo pripadajući par sila.

Zamenimo rezultujući sistem konvergentnih sila sa jednom silom jednakom glavnom vektoru originalnog sistema sila. Sistem parova sila koji nastaju tokom prenosa biće zamenjen jednim parom sa momentom jednakim geometrijskom zbiru momenata svih parova sila (tj. geometrijskom zbiru momenata prvobitnog sistema sila u odnosu na centar O).

Ovaj trenutak se zove glavni moment sistema sila u odnosu na centar O (Sl. 1.30).

Rice. 1.30. Dovođenje sistema snaga u centar

Dakle, svaki sistem sila uvijek može biti zamijenjen samo sa dva faktora sila - glavni vektor i glavni moment u odnosu na proizvoljno odabrani centar redukcije . Očigledno, glavni vektor sistema sila ne zavisi od izbora centra redukcije (kaže se da je glavni vektor invarijantan u odnosu na izbor centra redukcije). Očigledno je i da glavni moment nema ovo svojstvo, pa je uvijek potrebno naznačiti u odnosu na koji centar je glavni moment određen.

2. Dovođenje sistema sila u njegov najjednostavniji oblik

Mogućnost daljeg uprošćavanja proizvoljnih sistema sila zavisi od vrednosti njihovog glavnog vektora i glavnog momenta, kao i od uspešnog izbora centra redukcije. Mogući su sljedeći slučajevi:

a) , . U ovom slučaju sistem se svodi na par sila sa momentom čija vrijednost ne zavisi od izbora centra redukcije.

b) , . Sistem se svodi na rezultantu jednaku , čija linija djelovanja prolazi kroz centar O.

c) i međusobno su okomite. Sistem se svodi na rezultantu jednaku, ali ne prolazi kroz centar O(Sl. 1.31).

Rice. 1.31. Dovođenje sistema sila na rezultantu

Zamenimo glavni moment sa parom sila, kao što je prikazano na sl. 1.31. Hajde da definišemo R iz uslova da M 0 = R h. Zatim, na osnovu drugog aksioma statike, odbacimo uravnoteženi sistem dviju sila primijenjenih u tački O.

d) i paralelno. Sistem se pokreće pomoću dinamičkog vijka, sa osom koja prolazi kroz centar O(Sl. 1.32).

Rice. 1.32. Dinamički vijak

e) i nisu jednaki nuli, a istovremeno glavni vektor i glavni moment nisu paralelni i nisu okomiti jedan na drugi. Sistem se pokreće pomoću dinamičkog vijka, ali os ne prolazi kroz centar O(Sl. 1.33).


Rice. 1.33. Najopštiji slučaj redukcije sistema sila

Pretpostavimo da je proizvoljni ravan sistem sila sveden na jednu silu jednaku glavnom vektoru i primijenjenu na centar redukcije, te na jedan par sa momentom jednakim glavnom momentu
(Slika 57, A). Dokažimo da je proizvoljni ravan sistem sila koji se razmatra sveden u ovom opštem slučaju na rezultantnu silu
, čija linija djelovanja prolazi kroz tačku A, udaljen od odabranog centra redukcije O na daljinu
. Da bismo to učinili, transformiramo par trenutkom
pa ta snaga I
, koji čine ovaj par, pokazalo se da je po veličini jednak glavnom vektoru R". U ovom slučaju potrebno je odabrati krak para tako da njegov moment t
ostao jednak M 0. Za ovo, poluga para
očito se mora naći iz jednakosti

. (1)

Koristeći činjenicu da se par uvijek može pomjeriti u svojoj ravni djelovanja po želji, pomjerimo par
tako da njena snaga
se našao vezan za centar za adukciju O i suprotno od glavnog vektora
(Slika 57, b).

Prema tome, proizvoljni ravan sistem sila koji se razmatra je ekvivalentan sili
i par
. Odbacivanje snaga
I
kao uravnotežen, dobijamo da je čitav sistem sila koji se razmatra zamenjen jednom silom
, što je dakle rezultanta. U ovom slučaju, linija djelovanja rezultante proći će kroz tačku A, čiji je položaj u odnosu na odabrani centar redukcije određen formulom (1).

Ako se, kao rezultat dovođenja proizvoljnog ravan sistema sila, ispostavi da
, A
, tada se u ovom konkretnom slučaju ovaj sistem sila odmah zamjenjuje jednom silom, tj. rezultantom
, čija linija djelovanja prolazi kroz odabrani centar redukcije.

Problem 7. Do bodova IN I WITH na tijela primjenjuju se respektivno jednake po veličini i međusobno okomite sile I
, udaljen od tačke O tijela na jednakim udaljenostima
. Dovedite ovaj sistem sila do tačke O(Slika 58).

Rješenje. Prebacimo snage I paralelno sa nama do neke tačke O. Kao rezultat ovog prijenosa dobijamo (slika 58) sile
I
, primijenjen u tački O, i spojeni parovi
I
, ležeći u istoj ravni sa trenucima
I
(sile koje formiraju ove parove označene su na slici sa 58 crtica). Od geometrijskog sabiranja sila I , primijenjen u tački O, dobijamo glavni vektor ovog sistema sila

čiji je modul očigledno jednak

Sabiranjem spojnih parova dobijamo rezultantni par čiji je moment jednak glavnom momentu
datog sistema sila u odnosu na tačku O:

Dakle, ovaj sistem dvije sile I ima rezultantu

,

primijenjen na tački A, što je udaljeno od tačke O na daljinu

.

;
,

tj. rezultantni oblici sa obe date sile I jednaki uglovi od 45 0.

Zadatak 8. Vertikalne sile djeluju na rešetku mosta (slika 59)
t and
t na udaljenosti od 10 m i 40 m sa lijevog kraja rešetke i horizontalne sile
t u nivou gornje tetive rešetke, visina rešetke je 6 m. Dovedite sistem snaga ,I najjednostavniji oblik.

Rješenje. Koordinatne ose crtamo kao što je prikazano na slici 59, uzimajući ishodište koordinata u tački A. Nađimo projekcije glavnog vektora datog sistema sila na osu odabranog koordinatnog sistema:

gdje nalazimo modul glavnog vektora
:

T
.

Nađimo sada glavni moment datog sistema sila u odnosu na početak koordinata O:

t m
.

Shodno tome, ovaj sistem sila ima rezultantu
, čiji modul
T.

Sada pronađimo liniju akcije rezultante. Rezultatski trenutak u odnosu na porijeklo Aće se odrediti formulom

,

Gdje X I y - koordinate tačke koja leži na liniji djelovanja rezultante. Jer
t and
t, onda

.

WITH s druge strane, prema Varignonovoj teoremi o momentu rezultante (5, § 11) imamo

dakle,

.

Ovo je jednadžba linije djelovanja rezultante.

Uz pretpostavku u ovoj jednačini
, nalazimo da je tačka presjeka linije djelovanja rezultante sa gornjim tetivom rešetke koji se nalazi na udaljenosti
m sa lijevog kraja farme. Believing
m, nalazimo da je točka presjeka linije djelovanja rezultante sa donjom tetivom rešetke je na udaljenosti
m sa lijevog kraja farme. Ovako definisane veze su tačke preseka linija delovanja rezultante s gornjim i donjim tetivama rešetke u pravoj liniji, nalazimo liniju djelovanja rezultante .

Zamijenit ćemo ravan sistem sila primijenjenih u tačkama A, B, C, D:

1) sile F 1 ’, F 2 ’, F 3 ’, F 4 ’, primijenjene u tački O;

2) u parovima sila:

F 1 F 1 ': M 1 = M o (F 1) = F 1 a 1

F 2 F 2 ': M 2 = M o (F 2) = F 2 a 2

F 3 F 3 ': M 3 ​​= M o (F 3) = F 3 a 3

F 4 F 4 ': M 4 = M o (F 4) = F 4 a 4

Sile F 1 ’, F 2 ’, F 3 ’, F 4 ’ koje konvergiraju u tački O mogu se zamijeniti jednom silom (rezultantnom) F ch:

F gl = F 1 ' + F 2 ' + F 3 ' + F 4 ' = F 1 + F 2 + F 3 + F 4

F ch– glavni vektor sistema sila.

Rezultirajući parovi sila mogu se zamijeniti rezultujućim parom, čiji je moment M ch:

M gl = M 1 + M 2 + M 3 + M 4 = Σ M i = Σ M o (F i)

M gl - glavna tačka u vezi sa referentnom tačkom.

Ravan sistem sila u datoj tački O zamjenjuje se ekvivalentnim sistemom koji se sastoji od jedne sile (glavni vektor) i jednog para (glavni moment).

Teorema o momentu rezultante (Varinonova teorema)

Moment rezultantnog sistema sila u odnosu na proizvoljnu tačku jednak je algebarskom zbiru momenata komponentnih sila u odnosu na istu tačku.

M o (F Σ)= Σ M o (F i)

Jednačine ravnoteže za ravan sistem sila

F GL = 0;

M gl = ΣM o (F i) = 0.

Modul glavnog vektora može se odrediti kroz projekcije na koordinatne ose svih sila sistema.

F GL = (ΣF njih) 2 +(ΣF íu) 2 =0 iz ovoga slijede jednadžbe ravnoteže:

Σ F njih =0

Σ F íu =0

Σ M o (F i)=0

Drugi oblici jednadžbi ravnoteže:

Σ M A (F i)=0

Σ M V (F í)=0 (ABC ne leže na istom

Σ M C (F i)=0 direktno)

Σ M A (F i)=0 (x osa nije okomita

Σ M B (F í)=0 direktni AB)

Σ F njih =0

Za sistem paralelnih sila, odabirom jedne od projekcijskih osa paralelnih sa ovim silama (y-osa), a druge okomite na njih (x-osa), dobijamo dve jednačine ravnoteže:

Σ F íu =0

Σ M o (F i)=0

Σ M A (F i)=0

Σ M V (F i)=0

Algoritam za rješavanje problema

1. Odaberite objekat ravnoteže (telo ili tačku): razmatraćemo ravnotežu u odnosu na...

Na slici prikazujemo sve djelujuće sile, uključujući i reakcije veza.

3. Odaberite koordinatni sistem - preporučljivo je usmjeriti koordinatne ose paralelno ili okomito na tražene sile.

Sastavljamo jednadžbe ravnoteže za predmet proučavanja.

Σ F njih =0

Σ F íu =0

Σ M o (F i)=0

Iz rezultirajućih jednačina određujemo nepoznate veličine (određujemo reakcije).



Provjeravamo ispravnost rješenja jednadžbi.

Σ M p (F i)=0

Σ M e (F i)=0

5. Potporni uređaji za sisteme greda

Artikulirajuća podrška

Zglobno-fiksna forma i kruta brtva (štipanje)

Predmet:

"Centar gravitacije.

Geometrijske karakteristike ravnih presjeka"

Plan

1. Centar paralelnih sila i njegove koordinate.
2. Težište područja. Statistički momenti područja.
3. Rješavanje zadataka za određivanje koordinata težišta ravne složene figure.
4. Polarni i aksijalni momenti inercije.
5. Aksijalni momenti inercije oko paralelnih osa.
6. Određivanje momenata inercije kompozitnih presjeka pomoću tablica normalnog asortimana.

1. Centar paralelnih sila i njegove koordinate


Neka je zadan sistem paralelnih sila F 1, F 2, F 3, ..., Fn; poznate su koordinate tačaka C 1, C2, C3, ..., Cn primjene ovih sila (slika 42, b). Označimo tačku primjene rezultantnim slovom C, a njene koordinate x c, y c.
FΣ = F 1 + F 2 + F 3+…. + Fn = ΣF i . (1)



FΣ xs = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn = Σ F i x i ,

x c = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / FΣ = Σ F i x i / FΣ

FΣ = F 1+ F 2+ F 3+…+ Fn= Σ F njih c =
= F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / F 1+ F 2+ F 3+…+ Fn= Σ F i x i / F i (2)

Opisani metod dovođenja jedne sile u datu tačku može se primijeniti na bilo koji broj sila. Pretpostavimo da u tačkama tela A,B,C I D(Sl. 19) primijenjene sile 1 , 2 , 3 I 4 . Potrebno je ove sile dovesti do tačke O avion. Hajde da prvo damo snagu 1 , primijenjen na tački A. Primijenimo u tački O dvije sile ’ 1 I ’’ 1 , od kojih je svaki po modulu jednak datoj sili 1 , paralelno s njim i usmjereno u suprotnim smjerovima. Kao rezultat dovođenja sile 1 dobićemo moć ’ 1 , primijenjen u tački O, i par sila 1 ’’ 1 (sile koje formiraju par su označene crticama) sa ramenom a 1. Radeći isto sa silom 2 , primijenjen u tački IN, dobijamo snagu 2 , primijenjen u tački O, i par sila 2 ’’ 2 sa ramenom a 2 itd.

Ravan sistem sila primijenjenih u tačkama A, IN, WITH I D, zamijenili smo konvergentnim silama ’ 1 , ’ 2 , ’ 3 I ’ 4 , primijenjen u tački O, i parove sila sa momentima jednakim momentima datih sila u odnosu na tačku O:

M 1 = P 1 a 1 = M o ( 1); M 2 = P 2 a 2 = M o (2);

M 3 = – P 3 a 3 = M o ( 3); M 4 = – P 4 a 4 = M o (4).

Sile koje konvergiraju u tački mogu se zamijeniti jednom silom " , jednako geometrijskom zbiru komponenti,

" = " 1 + " 2 + " 3 + " 4 = 1 + 2 + 3 + 4 = i .(16)

Ova sila, jednaka geometrijskom zbiru datih sila, naziva se glavni vektor sistema sila.

Na osnovu pravila za sabiranje parova sila, iz se može zamijeniti rezultirajućim parom, čiji je moment jednak algebarskom zbiru momenata datih sila u odnosu na tačku O:

M o = M 1 + M 2 + M 3 + M 4 = i = o (i).(17)

Po analogiji sa glavnim vektorom, trenutkom M 0 parovi jednaki algebarskom zbiru momenata svih sila u odnosu na centar redukcije O, zvao glavni moment sistema u odnosu na dati centar redukcije O. dakle, u opštem slučaju, ravan sistem sila kao rezultat redukcije na datu tačku O zamenjuje se ekvivalentnim sistemom koji se sastoji od jedne sile - glavnog vektora - i jednog para, čiji se moment naziva glavni moment sile. dati sistem sila u odnosu na centar redukcije.

Potrebno je shvatiti da je glavni vektor ’ nije rezultanta datog sistema sila, jer ovaj sistem nije ekvivalentan jednoj sili ’. Samo u posebnom slučaju kada glavni moment nestane bit će glavni vektor rezultanta datog sistema sila. Pošto je glavni vektor jednak geometrijskom zbiru sila datog sistema, ni njegova veličina ni njegov pravac ne zavise od izbora centra redukcije. Veličina i znak glavnog trenutka M 0 zavise od položaja centra redukcije, budući da krakovi parova komponenti zavise od relativnog položaja sila i tačke (centra) u odnosu na koju se momenti uzimaju.

Mogu se javiti sljedeći slučajevi dovođenja sistema snaga:



1. " ≠ 0; M o ≠ 0 - opšti slučaj; sistem se svodi na glavni vektor i na glavni momenat.

2. " ≠ 0; M o = 0; sistem se svodi na jednu rezultantu jednaku glavnom vektoru sistema.

3. " = 0; M o ≠ 0; sistem se svodi na par sila čiji je moment jednak glavnom momentu.

4. " = 0; M o = 0; sistem je u ravnoteži.

Može se dokazati da u opštem slučaju, kada " ≠ 0 i M o ≠ 0, Uvijek postoji tačka u odnosu na koju je glavni moment sistema sila jednak nuli.

Razmotrimo ravan sistem sila koji je sveden na tačku O, tj. zamijenjen glavnim vektorom " ≠ 0 , primijenjen u tački O, i glavna poenta M o ≠ 0(Sl. 20).

Radi određenosti, pretpostavljamo da je glavni moment usmjeren u smjeru kazaljke na satu, tj. M o< 0. Oslikajmo ovaj glavni trenutak sa parom sila "" , čiji je modul izabran jednak modulu glavnog vektora " , tj. R =R '' = R '. Jedna od sila koje čine par je sila "" – prijavite se u redukcionom centru O, druga sila – u nekom trenutku WITH, čiji je položaj određen iz uslova: M o = OS*R. dakle,

OS =. (18)

Uložimo par sila "" tako da snaga "" bila usmjerena u smjeru suprotnom od glavnog vektora " . U tački O(Sl. 20) imamo dvije jednake i međusobno suprotne sile " I "" , usmjeren duž jedne prave linije; mogu se odbaciti (prema trećem aksiomu). Dakle, u odnosu na stvar WITH glavni moment sistema sila koji se razmatra jednak je nuli, a sistem se svodi na rezultantu .

§ 18. Teorema o momentu rezultante (Varinjonova teorema)

U opštem slučaju (vidi § 17), proizvoljni ravan sistem sila se svodi na glavni vektor " i glavna poenta M 0 u odnosu na izabrani centar redukcije, a glavni moment jednak je algebarskom zbiru momenata datih sila u odnosu na tačku O

M o = o (i).(A)

Pokazalo se da je moguće odabrati centar redukcije (na sl. 20 tačka WITH), u odnosu na koji će glavni moment sistema biti jednak nuli, a sistem sila će se svesti na jednu rezultantu jednaku po veličini glavnom vektoru ( R = R'). Odredimo moment rezultante u odnosu na tačku O. S obzirom da je rame OS sile jednake , dobijamo

M o () = R*OC = R = M o.(b)

Dvije veličine, odvojeno jednake trećoj, jednake su jedna drugoj, pa iz jednačina (a) i (b) nalazimo

M o () = o ( i).(19)

Rezultirajuća jednačina izražava Varignonovu teoremu: moment rezultantnog sistema sila u odnosu na proizvoljnu tačku jednak je algebarskom zbiru momenata komponentnih sila u odnosu na istu tačku.

Iz Varignonove teoreme slijedi da je glavni moment ravnog sistema sila u odnosu na bilo koju tačku koja leži na liniji djelovanja njegove rezultante jednak nuli.