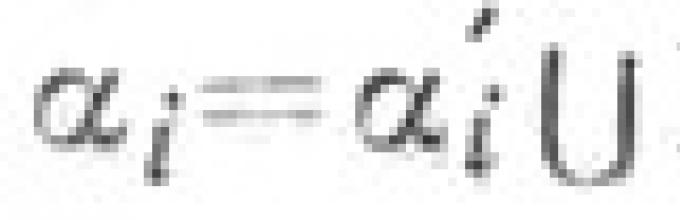Sastoji se od dvije različite zrake koje izlaze iz jedne tačke. Zraci se zovu strane U., a njihov zajednički početak je vrh U. Neka [ VA),[Ned) -
strane ugla, IN - njegov vrh je ravan definirana stranicama U. Figura dijeli ravan na dvije figure. ![]() i==l, 2, takođe se zove U. ili ravan ugao, tzv. unutrašnja oblast ravne U.
i==l, 2, takođe se zove U. ili ravan ugao, tzv. unutrašnja oblast ravne U.
Dva ugla se zovu jednaki (ili podudarni) ako se mogu poravnati tako da im se odgovarajuće stranice i vrhovi poklapaju. Iz bilo koje zrake na ravni, u datom pravcu od nje, može se nacrtati jedna os jednaka datoj osi.Poređenje ose se vrši na dva načina. Ako se greda posmatra kao par zraka sa zajedničkim ishodištem, onda da bi se razjasnilo pitanje koja je od dva snopa veća, potrebno je kombinovati vrhove grede i jedan par njihovih strana u jednoj ravni (vidi Slika 1). Ako se ispostavi da se druga strana jedne U. nalazi unutar druge U., onda kažu da je prva U. manja od druge. Drugi metod poređenja U. zasniva se na poređenju svakog U. sa određenim brojem. Jednako U. će odgovarati istim stepenima ili (vidi dolje), veće U. - veći broj, na manje - manje.

Zvala su dva U. susjedni ako imaju zajednički vrh i jednu stranu, a druge dvije strane čine pravu liniju (vidi sliku 2). Uopšteno govoreći, U. koje ima zajednički vrh i jednu zajedničku stranu se nazivaju. susjedni. U. je pozvao vertikalno ako su strane jedne produžetke iznad vrha strana druge.Okomite U. su jednake jedna drugoj. U., čije stranice čine pravu liniju, tzv. prošireno. Polovica proširenog U. pozvala. ravno U. Direktno U. može se ekvivalentno drugačije definirati: U. jednako svom susjednom, tzv. direktno. Unutrašnjost ravne ravni, koja ne prelazi raširenu, je konveksna oblast na ravni. Za mjernu jedinicu U. uzima se 90. razlomak direktnog U. tzv. stepen.

Koristi se i tzv. mjera U. Numerička vrijednost radijanske U. mjere je jednaka dužini luka koje presecaju stranice U. od jedinični krug. Jedan radijan je dodeljen U koji odgovara luku, koji je jednak njegovom poluprečniku. Prošireni U. jednak je radijanima.
Kada se dvije prave koje leže u istoj ravni seku sa trećom pravom linijom, formiraju se Us (vidi sliku 3): 1 i 5, 2 i 6, 4 i 8, 3 i 7 - tzv. prikladno; 2 i 5, 3 i 8 - unutrašnji jednostrani; 1 i 6, 4 i 7 - vanjski jednostrani; 3 i 5, 2 i 8 - iznutra ležeći poprečno; 1 i 7, 4 i 6 - ležeći poprečno sa vanjske strane.

U praksi U problemima je preporučljivo razmotriti rotaciju kao meru rotacije fiksne grede oko njenog početka do date pozicije. Ovisno o smjeru rotacije signala u ovom slučaju mogu se uzeti u obzir i pozitivni i negativni. Dakle, U. u ovom smislu može imati bilo koju vrijednost. Rotacija zraka se razmatra u trigonometrijskoj teoriji. funkcije: za bilo koje vrijednosti argumenta (U.), možete odrediti trigonometrijske vrijednosti. funkcije. Pojam geometrije u geometriji. Sistem, koji se zasniva na aksiomatici tačka-vektor, suštinski se razlikuje od definicija U. kao figure - u ovoj aksiomatici U. se shvata kao određena metrika. veličina koja se odnosi na dva vektora koristeći operaciju množenja skalarnog vektora. Naime, svaki par vektora a i b definira određeni ugao - broj pridružen vektorima formulom
![]()
Gdje ( a, b) -
skalarni proizvod vektora.
Koncept U. kao ravne figure i kao određene numeričke vrijednosti koristi se u raznim geometrijama. problemi u kojima se U. određuje na poseban način. Dakle, pod oblikom između krivulja koje se sijeku koje imaju određene tangente u tački sjecišta, podrazumijevamo oblik koji čine te tangente.
Za ugao između prave i ravni se uzima ugao koji čine prava linija i njena pravougaona projekcija na ravan; mjeri se u rasponu od 0
Matematička enciklopedija. - M.: Sovjetska enciklopedija. I. M. Vinogradov. 1977-1985.
Sinonimi:Pogledajte šta je "ANGLE" u drugim rječnicima:
žeravica- ugao / vrpca / ... Morfemsko-pravopisni rječnik
Muž. prijelom, pregib, koleno, lakat, izbočenje ili nabor (udubljenje) na jednoj strani. Linearni ugao, bilo koje dvije suprotne linije i njihov interval; ugaona ravan ili u ravnima, susret dve ravni ili zidova; ugao je debeo, telo, spaja se u jedno... Rječnik Dahl
Ugao, oko ugla, na (u) uglu i (mat.) u uglu, m. 1. Deo ravni između dve prave koje izlaze iz jedne tačke (mat.). Vrh ugla. Strane ugla. Mjerenje ugla u stepenima. Pravi ugao. (90°). Oštar ugao. (manje od 90°). Tupi ugao…… Ushakov's Explantatory Dictionary
CORNER- (1) napadni ugao između smera strujanja vazduha koji struji na krilo aviona i tetive dela krila. Vrijednost sile dizanja ovisi o ovom kutu. Ugao pod kojim je sila dizanja maksimalna naziva se kritični napadni ugao. U...... Velika politehnička enciklopedija
- (ravno) geometrijska figura, formirana od dvije zrake (stranice ugla) koje izlaze iz jedne tačke (vrh jednog ugla). Bilo koji ugao sa vrhom u centru nekog kruga ( centralni ugao) definira luk AB na kružnici, omeđen tačkama ... ... Veliki enciklopedijski rječnik
Glava ugla, iza ugla, medveđi ugao, nedovršeni ugao, u svim uglovima... Rečnik ruskih sinonima i izraza sličnih po značenju. ispod. ed. N. Abramova, M.: Ruski rječnici, 1999. vrh ugla, tačka ugla; ležaj, zaklon, deviatina, pravac,...... Rečnik sinonima
ugao- ugao, štap. kut; rečenica o uglju, u (na)ćošku i u govoru matematičara u uglju; pl. uglovi, šipka. uglovi U predloškim i stabilnim kombinacijama: iza ugla i dozvoljeno je ići iza ugla (ući, skrenuti, itd.), iz ugla u ugao (pomak, pozicija, itd.), ugao... ... Rečnik teškoća izgovora i naglaska u savremenom ruskom jeziku
UGAO, ugao, oko ugla, na (u) uglu, muž. 1. (u uglu.). u geometriji: ravna figura, formirana od dvije zrake (u 3 vrijednosti) koje izlaze iz jedne tačke. Vrh ugla. Direktno y. (90°). Acute u. (manje od 90°). Dumb u. (više od 90°). Spoljašnje i unutrašnje...... Ozhegov's Explantatory Dictionary
ugao- UGAO, ugao, m. Četvrtina opklade, kada se objavi, ivica karte je savijena. ◘ As i pikova dama sa kornerom // Ubijen. A.I. Polezhaev. Jedan dan u Moskvi, 1832. ◘ Nakon večere, razbacuje crvenoke po stolu, miješa karte; igrači razbijaju špilove..... Kartaška terminologija i žargon iz 19. stoljeća
Definicija
Geometrijska figura koja se sastoji od svih tačaka ravnine zatvorene između dve zrake koje izlaze iz jedne tačke naziva se ravan ugao.
Definicija
Ugao između dva ukrštanje ravno je vrijednost najmanjeg ravnog ugla na presjeku ovih pravih. Ako su dvije prave paralelne, tada se ugao između njih uzima jednak nuli.
Ugao između dvije linije koje se sijeku (ako se ravni uglovi mjere u radijanima) može imati vrijednosti od nule do $\dfrac(\pi)(2)$.
Definicija
Ugao između dve linije koje se seku je veličina jednaka uglu između dve prave koje se seku paralelne sa onima koje se seku. Ugao između pravih $a$ i $b$ je označen sa $\ugao (a, b)$.
Ispravnost uvedene definicije proizlazi iz sljedeće teoreme.
Teorema o ravnim uglovima sa paralelnim stranicama
Veličine dvaju konveksnih ravnih ugla sa paralelnim i identično usmerenim stranicama su jednake.
Dokaz
Ako su uglovi ravni, onda su oba jednaka $\pi$. Ako nisu rasklopljeni, iscrtavamo jednake segmente $ON=O_1ON_1$ i $OM=O_1M_1$ na odgovarajućim stranicama uglova $\ugla AOB$ i $\ugla A_1O_1B_1$.
Četvorougao $O_1N_1NO$ je paralelogram jer su njegove suprotne strane $ON$ i $O_1N_1$ jednake i paralelne. Isto tako, četverougao $O_1M_1MO$ je paralelogram. Otuda $NN_1 = OO_1 = MM_1$ i $NN_1 \paralelno OO_1 \paralelno MM_1$, dakle, $NN_1=MM_1$ i $NN_1 \paralelno MM_1$ po tranzitivnosti. Četvorougao $N_1M_1MN$ je paralelogram, jer su mu suprotne strane jednake i paralelne. To znači da su segmenti $NM$ i $N_1M_1$ jednaki. Trokuti $ONM$ i $O_1N_1M_1$ su jednaki prema trećem kriterijumu jednakosti trouglova, što znači odgovarajućim uglovima$\ugao NOM$ i $\ugao N_1O_1M_1$ su jednaki.
Neka su dva vektora različita od nule i dati na ravni ili u trodimenzionalnom prostoru. Odgodimo sa proizvoljne tačke O vektori i . Tada vrijedi sljedeća definicija.
Definicija.
Ugao između vektora a ugao između zraka naziva se O.A. I O.B..
Ugao između vektora i će biti označen kao .
Ugao između vektora može uzeti vrijednosti iz 0 do ili, što je ista stvar, od do.
Kada su oba vektora kousmjerena, kada su vektori također suprotno usmjereni.
Definicija.
Vektori se nazivaju okomito, ako je ugao između njih jednak (radijanima).
Ako je barem jedan od vektora nula, tada ugao nije definiran.
Pronalaženje ugla između vektora, primjera i rješenja.
Kosinus ugla između vektora i , a samim tim i sam ugao, u opštem slučaju može se naći ili korišćenjem skalarnog proizvoda vektora, ili pomoću kosinusne teoreme za trokut izgrađen na vektorima i .
Pogledajmo ove slučajeve.
Po definiciji, skalarni proizvod vektora je . Ako su vektori i različiti od nule, tada možemo podijeliti obje strane posljednje jednakosti proizvodom dužina vektora i , i dobićemo formula za pronalaženje kosinusa ugla između vektora koji nisu nula: . Ova formula se može koristiti ako su poznate dužine vektora i njihov skalarni proizvod.
Primjer.
Izračunajte kosinus kuta između vektora i , i također pronađite sam kut ako su dužine vektora i jednake 3 I 6 respektivno, a njihov skalarni proizvod je jednak -9 .
Rješenje.
Iskaz problema sadrži sve količine potrebne za primjenu formule. Izračunavamo kosinus ugla između vektora i: .
Sada nalazimo ugao između vektora: .
Odgovori:
Postoje problemi gdje su vektori specificirani koordinatama u pravokutnom koordinatnom sistemu na ravni ili u prostoru. U ovim slučajevima, da biste pronašli kosinus ugla između vektora, možete koristiti istu formulu, ali u koordinatnom obliku. Hajde da ga uzmemo.
Dužina vektora je kvadratni korijen zbira kvadrata njegovih koordinata, skalarni proizvod vektora jednak je zbiru proizvoda odgovarajućih koordinata. dakle, formula za izračunavanje kosinusa ugla između vektora na ravni ima oblik , a za vektore u trodimenzionalnom prostoru - .
Primjer.
Pronađite ugao između vektora datih u pravougaonom koordinatnom sistemu.
Rješenje.
Možete odmah koristiti formulu:
Ili možete koristiti formulu da pronađete kosinus ugla između vektora, nakon što je prethodno izračunao dužine vektora i skalarni proizvod preko koordinata:
odgovor:
Problem se svodi na prethodni slučaj kada su date koordinate tri tačke (npr A, IN I WITH) u pravougaonom koordinatnom sistemu i trebate pronaći neki ugao (na primjer, ).
Doista, kut je jednak kutu između vektora i . Koordinate ovih vektora su izračunate kao razlika između odgovarajućih koordinata krajnje i početne tačke vektora.
Primjer.
Na ravni su koordinate tri tačke date u Dekartovom koordinatnom sistemu. Pronađite kosinus kuta između vektora i .
Rješenje.
Odredimo koordinate vektora i koordinate datih tačaka:
Sada koristimo formulu da pronađemo kosinus ugla između vektora na ravni u koordinatama:
odgovor:
Ugao između vektora i može se također izračunati po kosinus teorema. Ako odgodimo sa tačke O vektora i , zatim po kosinusnoj teoremi u trokutu OAV možemo napisati, što je ekvivalentno jednakosti, iz koje nalazimo kosinus ugla između vektora. Da bismo primijenili rezultirajuću formulu, potrebne su nam samo dužine vektora i , koje se lako mogu pronaći iz koordinata vektora i . Međutim, ova metoda se praktički ne koristi, jer je kosinus kuta između vektora lakše pronaći pomoću formule.
Kalkulacija ortogonalna projekcija(sopstvena projekcija):
Projekcija vektora na osu l jednaka je proizvodu modula vektora i kosinusa ugla φ između vektora i ose, tj. pr cosφ.
Dok: Ako je φ=< , то пр l =+ = *cos φ.
Ako je φ> (φ≤), tada pr l =- =- * cos( -φ) = cosφ (vidi sliku 10)
Ako je φ= , tada je pr l = 0 = cos φ.
Posljedica: Projekcija vektora na osu je pozitivna (negativna) ako vektor formira oštar (tupi) ugao sa osom, a jednaka je nuli ako je ovaj ugao pravi.
Posljedica: Projekcije jednakih vektora na istu osu su jednake jedna drugoj.
Izračunavanje ortogonalne projekcije zbira vektora (svojstvo projekcije):
Projekcija sume nekoliko vektora na istu osu jednaka je zbiru njihovih projekcija na ovu osu.
Doc: Neka je, na primjer, = + + . Imamo pr l =+ =+ + - , tj. pr l ( + + ) = pr l + pr l + pr l (vidi sliku 11)
RICE. jedanaest
Izračunavanje proizvoda vektora i broja:
Kada se vektor pomnoži brojem λ, njegova projekcija na osu se također množi ovim brojem, tj. pr l (λ* )= λ* pr l .
Dokaz: Za λ > 0 imamo pr l (λ* )= *cos φ = λ* φ = λ*pr l
Kada je λl (λ* )= *cos( -φ)=- * (-cosφ) = * cosφ= λ *pr l .
Svojstvo vrijedi i kada
Dakle, linearne operacije na vektorima dovode do odgovarajućeg linearne operacije preko projekcija ovih vektora.
Ovaj materijal posvećen je konceptu kao što je kut između dvije linije koje se sijeku. U prvom paragrafu ćemo objasniti šta je to i pokazati na ilustracijama. Zatim ćemo pogledati načine na koje možete pronaći sinus, kosinus ovog kuta i sam kut (zasebno ćemo razmotriti slučajeve s ravninom i trodimenzionalnim prostorom), dat ćemo potrebne formule i pokazati primjerima tačno kako se koriste u praksi.
Da bismo razumjeli koliki je ugao koji nastaje kada se dvije prave ukrštaju, moramo se sjetiti same definicije ugla, okomice i točke sjecišta.
Definicija 1
Dve prave zovemo da se seku ako imaju jednu zajednička tačka. Ova tačka se naziva tačka preseka dve prave.
Svaka prava linija je podijeljena presječnom točkom na zrake. Obje prave prave 4 ugla, od kojih su dva okomita, a dva susjedna. Ako znamo mjeru jednog od njih, onda možemo odrediti preostale.
Recimo da znamo da je jedan od uglova jednak α. U ovom slučaju, ugao koji je okomit u odnosu na njega također će biti jednak α. Da bismo pronašli preostale uglove, moramo izračunati razliku 180° - α. Ako je α jednako 90 stepeni, tada će svi uglovi biti pravi uglovi. Prave koje se sijeku pod pravim uglom nazivaju se okomiti (poseban članak posvećen je konceptu okomitosti).
Pogledajte sliku:
Pređimo na formulisanje glavne definicije.
Definicija 2
Ugao koji formiraju dvije linije koje se seku je mjera manjeg od 4 ugla koji formiraju ove dvije prave.
Iz definicije se mora izvući važan zaključak: veličina ugla u ovom slučaju bit će izražena bilo kojim pravi broj u intervalu (0, 90). Ako su linije okomite, tada će ugao između njih u svakom slučaju biti jednak 90 stepeni.

Sposobnost pronalaženja mjere ugla između dvije linije koje se seku je korisna za rješavanje mnogih praktični problemi. Metoda rješenja može se odabrati između nekoliko opcija.
Za početak možemo uzeti geometrijske metode. Ako znamo nešto o komplementarnim uglovima, onda ih možemo povezati sa uglom koji nam je potreban koristeći svojstva jednakih ili sličnih figura. Na primjer, ako znamo stranice trokuta i trebamo izračunati ugao između linija na kojima se te stranice nalaze, tada je kosinusni teorem prikladan za naše rješenje. Ako imamo uslov pravougaonog trougla, tada će nam za proračune trebati i poznavanje sinusa, kosinusa i tangenta ugla.
Koordinatna metoda je također vrlo pogodna za rješavanje problema ovog tipa. Hajde da objasnimo kako ga pravilno koristiti.
Imamo pravougaoni (kartezijanski) koordinatni sistem O x y, u kojem su date dvije prave. Označimo ih slovima a i b. Prave se mogu opisati pomoću nekih jednačina. Originalne linije imaju presek M. Kako odrediti traženi ugao (označimo ga α) između ovih pravih?
Počnimo sa formulisanjem osnovnog principa nalaženja ugla pod datim uslovima.
Znamo da je koncept prave linije usko povezan sa konceptima kao što su vektor pravca i vektor normale. Ako imamo jednadžbu određene linije, možemo uzeti koordinate ovih vektora iz nje. To možemo učiniti za dvije linije koje se seku odjednom.
Ugao sastavljen od dvije linije koje se ukrštaju može se pronaći pomoću:
- ugao između vektora smjera;
- ugao između normalnih vektora;
- ugao između vektora normale jedne linije i vektora smjera druge.
Sada pogledajmo svaku metodu posebno.
1. Pretpostavimo da imamo pravu a sa vektorom smjera a → = (a x, a y) i pravu b sa vektorom smjera b → (b x, b y). Sada nacrtajmo dva vektora a → i b → iz tačke preseka. Nakon ovoga ćemo vidjeti da će svaki biti smješten na svojoj pravoj liniji. Onda imamo četiri opcije za njih relativnu poziciju. Pogledajte ilustraciju:

Ako ugao između dva vektora nije tup, onda će to biti ugao koji nam treba između pravih a i b koji se sijeku. Ako je tup, onda će željeni ugao biti jednak uglu pored ugla a →, b → ^. Dakle, α = a → , b → ^ ako je a → , b → ^ ≤ 90 °, i α = 180 ° - a → , b → ^ ako je a → , b → ^ > 90 ° .
Na osnovu činjenice da kosinus jednakih uglova su jednake, možemo prepisati rezultirajuće jednakosti na sljedeći način: cos α = cos a → , b → ^ , ako je a → , b → ^ ≤ 90 ° ; cos α = cos 180 ° - a →, b → ^ = - cos a →, b → ^, ako je a →, b → ^ > 90 °.
U drugom slučaju korištene su formule redukcije. dakle,
cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^
Napišimo posljednju formulu riječima:
Definicija 3
Kosinus ugla kojeg formiraju dvije prave linije koje se seku bit će jednak modulu kosinusa ugla između njegovih vektora smjera.
Opšti oblik formule za kosinus ugla između dva vektora a → = (a x , a y) i b → = (b x , b y) izgleda ovako:
cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Iz njega možemo izvesti formulu za kosinus ugla između dvije date prave:
cos α = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Tada se sam ugao može pronaći pomoću sljedeće formule:
α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Ovdje su a → = (a x , a y) i b → = (b x , b y) vektori smjera datih linija.
Dajemo primjer rješavanja problema.
Primjer 1
U pravougaonom koordinatnom sistemu na ravni date su dve prave a i b koje se seku. Mogu se opisati parametarskim jednačinama x = 1 + 4 · λ y = 2 + λ λ ∈ R i x 5 = y - 6 - 3. Izračunajte ugao između ovih linija.
Rješenje
U našem smo stanju parametarska jednačina, što znači da za ovu liniju možemo odmah zapisati koordinate njenog vektora smjera. Da bismo to učinili, moramo uzeti vrijednosti koeficijenata za parametar, tj. prava linija x = 1 + 4 · λ y = 2 + λ λ ∈ R će imati vektor pravca a → = (4, 1).
Druga ravna linija je opisana pomoću kanonska jednačina x 5 = y - 6 - 3 . Ovdje možemo uzeti koordinate iz nazivnika. Dakle, ova prava ima vektor smjera b → = (5 , - 3) .
Zatim prelazimo direktno na pronalaženje ugla. Da biste to učinili, jednostavno zamijenite postojeće koordinate dva vektora u gornju formulu α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2 . Dobijamo sljedeće:
α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45 °
Odgovori: Ove ravne linije formiraju ugao od 45 stepeni.
Sličan problem možemo riješiti pronalaženjem ugla između normalnih vektora. Ako imamo pravu a sa vektorom normale n a → = (n a x , n a y) i pravu b sa vektorom normale n b → = (n b x , n b y), tada će ugao između njih biti jednak uglu između n a → i n b → ili ugao koji će biti susedan sa n a →, n b → ^. Ova metoda je prikazana na slici:

Formule za izračunavanje kosinusa ugla između linija koje se sijeku i samog ugla pomoću koordinata normalnih vektora izgledaju ovako:
cos α = cos n a → , n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2 α = a r c cos n a x n b x + n a y + n x n b y 2 + n b x 2 2
Ovdje n a → i n b → označavaju vektore normale dvije date prave.
Primjer 2
U pravougaonom koordinatnom sistemu date su dve prave pomoću jednačina 3 x + 5 y - 30 = 0 i x + 4 y - 17 = 0. Pronađite sinus i kosinus ugla između njih i veličinu samog ugla.
Rješenje
Originalne linije su specificirane pomoću normalne jednačine prava linija oblika A x + B y + C = 0. Vektor normale označavamo sa n → = (A, B). Nađimo koordinate prvog vektora normale za jednu liniju i zapišemo ih: n a → = (3, 5) . Za drugu liniju x + 4 y - 17 = 0, vektor normale će imati koordinate n b → = (1, 4). Sada dodajmo dobijene vrijednosti formuli i izračunajmo ukupno:
cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34
Ako znamo kosinus ugla, onda možemo izračunati njegov sinus koristeći osnovni trigonometrijski identitet. Pošto ugao α koji formiraju prave linije nije tup, onda je sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.
U ovom slučaju, α = a r c cos 23 2 34 = a r c sin 7 2 34.
Odgovor: cos α = 23 2 34, sin α = 7 2 34, α = a r c cos 23 2 34 = a r c sin 7 2 34
Analizirajmo posljednji slučaj - pronalaženje ugla između pravih ako znamo koordinate vektora smjera jedne prave i vektora normale druge.
Pretpostavimo da prava a ima vektor pravca a → = (a x , a y) , a prava b ima vektor normale n b → = (n b x , n b y) . Ove vektore treba da stavimo po strani od tačke preseka i razmotrimo sve opcije za njihove relativne pozicije. Pogledajte na slici:

Ako ugao između datih vektora nije veći od 90 stepeni, ispada da će dopuniti ugao između a i b u pravi ugao.
a → , n b → ^ = 90 ° - α ako je a → , n b → ^ ≤ 90 ° .
Ako je manji od 90 stepeni, dobijamo sledeće:
a → , n b → ^ > 90 ° , zatim a → , n b → ^ = 90 ° + α
Koristeći pravilo jednakosti kosinusa jednakih uglova, pišemo:
cos a → , n b → ^ = cos (90 ° - α) = sin α za a → , n b → ^ ≤ 90 ° .
cos a → , n b → ^ = cos 90 ° + α = - sin α za a → , n b → ^ > 90 ° .
dakle,
sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , a → , n b → ^ > 0 - cos a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^
Hajde da formulišemo zaključak.
Definicija 4
Da biste pronašli sinus ugla između dvije prave koje se sijeku na ravni, morate izračunati modul kosinusa ugla između vektora smjera prve linije i vektora normale druge.
Zapišimo potrebne formule. Pronalaženje sinusa ugla:
sin α = cos a → , n b → ^ = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Pronalaženje samog ugla:
α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Ovdje je a → vektor smjera prve linije, a n b → je vektor normale druge.
Primjer 3
Dvije prave koje se seku date su jednadžbama x - 5 = y - 6 3 i x + 4 y - 17 = 0. Pronađite ugao preseka.
Rješenje
Koordinate vodilice i vektora normale uzimamo iz datih jednadžbi. Ispada a → = (- 5, 3) i n → b = (1, 4). Uzimamo formulu α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 i izračunavamo:
α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34
Napominjemo da smo uzeli jednadžbe iz prethodnog problema i dobili potpuno isti rezultat, ali na drugačiji način.
odgovor:α = a r c sin 7 2 34
Predstavimo još jedan način za pronalaženje željenog ugla koristeći ugaone koeficijente datih pravih linija.
Imamo pravu a, koja je definisana u pravougaonom koordinatnom sistemu pomoću jednačine y = k 1 x + b 1, i pravu b, definisanu kao y = k 2 x + b 2. Ovo su jednadžbe linija sa nagibima. Da bismo pronašli ugao presjeka, koristimo formulu:
α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, gdje su k 1 i k 2 nagibi datih pravih. Za dobijanje ovog zapisa korištene su formule za određivanje ugla kroz koordinate vektora normale.
Primjer 4
Postoje dvije prave koje se seku u ravni, date jednadžbama y = - 3 5 x + 6 i y = - 1 4 x + 17 4. Izračunajte vrijednost ugla presjeka.
Rješenje
Ugaoni koeficijenti naših linija jednaki su k 1 = - 3 5 i k 2 = - 1 4. Dodajmo ih formuli α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 i izračunajmo:
α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = a r c cos 23 2 34
odgovor:α = a r c cos 23 2 34
U zaključcima ovog paragrafa treba napomenuti da se formule za pronalaženje ugla koje su ovdje date ne moraju učiti napamet. Da biste to učinili, dovoljno je znati koordinate vodilica i/ili vektora normale datih linija i moći ih odrediti pomoću različite vrste jednačine. Ali bolje je zapamtiti ili zapisati formule za izračunavanje kosinusa kuta.
Kako izračunati ugao između linija koje se seku u prostoru
Proračun takvog ugla može se svesti na izračunavanje koordinata vektora pravca i određivanje veličine ugla koji ovi vektori formiraju. Za takve primjere koristi se isto rezonovanje koje smo dali prije.
Pretpostavimo da imamo pravougaoni koordinatni sistem koji se nalazi u trodimenzionalnom prostoru. Sadrži dvije prave a i b sa presječnom tačkom M. Da bismo izračunali koordinate vektora smjera, moramo znati jednačine ovih linija. Označimo vektore smjera a → = (a x , a y , a z) i b → = (b x , b y , b z) . Za izračunavanje kosinusa ugla između njih koristimo formulu:
cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Da bismo pronašli sam ugao, potrebna nam je ova formula:
α = a r c cos a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Primjer 5
Imamo liniju definisanu u trodimenzionalnom prostoru pomoću jednačine x 1 = y - 3 = z + 3 - 2. Poznato je da se seče sa O z osom. Izračunajte ugao presjeka i kosinus tog ugla.
Rješenje
Označimo ugao koji treba izračunati slovom α. Zapišimo koordinate vektora pravca za prvu pravu – a → = (1, - 3, - 2) . Za osovinu applicate možemo uzeti koordinatni vektor k → = (0, 0, 1) kao vodič. Dobili smo potrebne podatke i možemo ih dodati u željenu formulu:
cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2
Kao rezultat toga, otkrili smo da će ugao koji nam treba biti jednak a r c cos 1 2 = 45 °.
odgovor: cos α = 1 2 , α = 45 ° .
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter