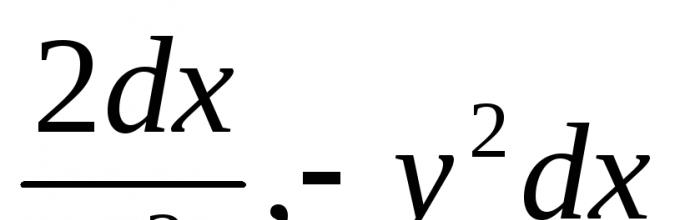Generalizovane homogene jednadžbe drugog reda. Predavanje diferencijalne jednadžbe. Uopštena homogena jednačina

Jednačina M(x, y) dx+ N(x, y) dy=0 naziva se generalizirani homogen ako je moguće odabrati takav broj k, da lijeva strana ove jednačine postaje homogena funkcija nekog stepena m relativno x, y, dx I dy pod uslovom da x smatra se vrijednošću prve dimenzije, y – k‑ th merenja , dx I dy – odnosno nula i (k-1) th merenja. Na primjer, ovo bi bila jednadžba. (6.1)

Vrijedi pod pretpostavkama napravljenim u vezi mjerenja

x, y, dx I dy pripadnici leve strane
I dy će imati dimenzije -2, 2 respektivno k I k-1. Izjednačavajući ih, dobijamo uslov koji traženi broj mora da zadovolji k: -2 = 2k = k-1. Ovaj uslov je zadovoljen kada k = -1 (sa ovim k svi članovi na lijevoj strani jednačine koja se razmatra imat će dimenziju -2). Prema tome, jednačina (6.1) je generalizovana homogena.

Generalizirana homogena jednadžba se reducira na jednadžbu s odvojivim varijablama korištenjem zamjene
, Gdje z– nova nepoznata funkcija. Integrirajmo jednačinu (6.1) pomoću naznačene metode. Jer k = -1, onda
, nakon čega dobijamo jednačinu.

Integrirajući ga, nalazimo
, gdje
. Ovo je opšte rješenje jednačine (6.1).

§ 7. Linearne diferencijalne jednačine 1. reda.

Linearna jednačina 1. reda je jednačina koja je linearna u odnosu na željenu funkciju i njen izvod. Izgleda:

, (7.1)

Gdje P(x) I Q(x) – date kontinuirane funkcije od x. Ako je funkcija
, tada jednačina (7.1) ima oblik:
(7.2)

i inače se naziva linearna homogena jednačina
naziva se linearna nehomogena jednačina.

Linearna homogena diferencijalna jednadžba (7.2) je jednadžba sa odvojivim varijablama:

(7.3)

Izraz (7.3) je opšte rješenje jednačine (7.2). Pronaći opće rješenje jednadžbe (7.1), u kojoj je funkcija P(x) označava istu funkciju kao u jednadžbi (7.2), primjenjujemo tehniku koja se zove metoda varijacije proizvoljne konstante i sastoji se od sljedećeg: pokušat ćemo odabrati funkciju C=C(x) tako da bi opšte rješenje linearne homogene jednačine (7.2) bilo rješenje nehomogene linearne jednačine (7.1). Tada za derivaciju funkcije (7.3) dobijamo:

Zamjenom pronađenog izvoda u jednačinu (7.1) imat ćemo:

ili
.

Gdje
, Gdje - proizvoljna konstanta. Kao rezultat, opće rješenje nehomogene linearne jednačine (7.1) će biti (7.4)

Prvi član u ovoj formuli predstavlja opšte rešenje (7.3) linearne homogene diferencijalne jednačine (7.2), a drugi član formule (7.4) je posebno rešenje linearne nehomogene jednačine (7.1), dobijeno iz opšte ( 7.4) sa
. Ovaj važan zaključak ističemo u obliku teoreme.

Teorema. Ako je poznato jedno određeno rješenje linearne nehomogene diferencijalne jednadžbe
, tada sva ostala rješenja imaju oblik
, Gdje
- opšte rješenje odgovarajuće linearne homogene diferencijalne jednadžbe.

Međutim, treba napomenuti da se za rješavanje linearne nehomogene diferencijalne jednadžbe 1. reda (7.1) češće koristi druga metoda, koja se ponekad naziva i Bernoullijeva metoda. Rješenje jednačine (7.1) tražit ćemo u obliku
. Onda
. Zamenimo pronađeni derivat u originalnu jednačinu:
.

Kombinirajmo, na primjer, drugi i treći član posljednjeg izraza i izdvojimo funkciju u(x) iza zagrade:
(7.5)

Zahtijevamo da se zagrada poništi:
.

Rešimo ovu jednačinu postavljanjem proizvoljne konstante C jednako nuli:
. Sa pronađenom funkcijom v(x) Vratimo se na jednačinu (7.5):
.

Rešavajući to, dobijamo:
.

Prema tome, opšte rješenje jednačine (7.1) ima oblik.

def 1 DU tip

pozvao homogena diferencijalna jednadžba prvog reda(ODU).

Th 1 Neka su za funkciju ispunjeni sljedeći uvjeti:

1) kontinuirano na

Tada ODE (1) ima opšti integral, koji je dat formulom:

gdje je neki antiderivat funkcije With je proizvoljna konstanta.

Napomena 1 Ako je za neke ispunjen uslov, onda u procesu rješavanja ODE (1) rješenja oblika mogu biti izgubljena; takvi slučajevi se moraju pažljivije tretirati i svaki od njih posebno provjeriti.

Dakle, iz teoreme Th1 trebalo bi opšti algoritam za rješavanje ODE (1):

1) Napravite zamjenu:

2) Tako će se dobiti diferencijalna jednačina sa odvojivim varijablama, koju treba integrisati;

3) Povratak na stare varijable;

4) Provjerite vrijednosti za njihovu uključenost u rješenje originalni daljinski, pod kojim će uslov biti zadovoljen

5) Zapišite odgovor.

Primjer 1 Riješite DE (4).

Rješenje: DE (4) je homogena diferencijalna jednadžba, jer ima oblik (1). Napravimo promjenu (3), ovo će dovesti jednačinu (4) u oblik:

Jednačina (5) je opći integral DE (4).

Imajte na umu da pri odvajanju varijabli i dijeljenju sa, rješenja mogu biti izgubljena, ali ovo nije rješenje za DE (4), što se lako provjerava direktnom zamjenom u jednakost (4), budući da ova vrijednost nije uključena u domenu definicije originalnog DE.

odgovor:

Napomena 2 Ponekad možete napisati ODE u terminima diferencijala varijabli X I u. Preporučljivo je preći sa ove oznake daljinskog upravljača na izraz kroz izvod i tek onda izvršiti zamjenu (3).

Diferencijalne jednadžbe svedene na homogene.

def 2 Funkcija se poziva homogena funkcija stepena k u oblasti, za koje će biti zadovoljena jednakost:

Evo najčešćih tipova diferencijalnih jednadžbi koje se mogu svesti na oblik (1) nakon različitih transformacija.

1) gdje je funkcija je homogena, stepen nula, odnosno vrijedi jednakost: DE (6) se lako svodi na oblik (1), ako stavimo , koji se dalje integrira zamjenom (3).

2) (7), gdje su funkcije homogene istog stepena k . DE oblika (7) je također integriran korištenjem supstitucije (3).

Primjer 2 Riješite DE (8).

Rješenje: Pokažimo da je DE (8) homogen. Podijelimo s onim što je moguće, jer to nije rješenje za DE (8).

Napravimo promjenu (3), ovo će dovesti jednačinu (9) u oblik:

Jednačina (10) je opći integral DE (8).

Imajte na umu da prilikom odvajanja varijabli i dijeljenja sa, rješenja koja odgovaraju vrijednostima i mogu biti izgubljena. Provjerimo ove izraze. Zamijenimo ih u DE (8):

odgovor:

Zanimljivo je napomenuti da se prilikom rješavanja ovog primjera pojavljuje funkcija koja se zove “znak” broja X(čita " signum x"), definisan izrazom:

Napomena 3 Svođenje DE (6) ili (7) na oblik (1) nije potrebno; ako je očigledno da je DE homogen, tada možete odmah izvršiti zamjenu

3) DE oblika (11) je integriran kao ODE ako je , a zamjena se inicijalno izvodi:

(12), gdje je rješenje sistema: (13), a zatim koristite zamjenu (3) za funkciju. Nakon što dobiju opći integral, vraćaju se na varijable X I at.

Ako , onda, uz pretpostavku u jednačini (11), dobijamo diferencijalnu jednačinu sa odvojivim varijablama.

Primjer 3 Riješite Cauchyjev problem (14).

Rješenje: Pokažimo da je DE (14) reduciran na homogeni DE i integrisan prema gornjoj šemi:

Rešimo nehomogeni sistem linearnih algebarskih jednadžbi (15) koristeći Cramerovu metodu:

Napravimo promjenu varijabli i integrirajmo rezultirajuću jednačinu:

(16) – Opšti integral DE (14). Prilikom razdvajanja varijabli rješenja mogu biti izgubljena prilikom dijeljenja izrazom, koji se može dobiti eksplicitno nakon rješavanja kvadratne jednadžbe. Međutim, oni su uzeti u obzir u općem integralu (16) na

Nađimo rješenje za Cauchyjev problem: zamijenimo vrijednosti i u opći integral (16) i pronađemo With.

Dakle, parcijalni integral će biti dat formulom:

odgovor:

4) Moguće je svesti neke diferencijalne jednadžbe na homogene za novu, još nepoznatu funkciju ako primijenimo zamjenu oblika:

U ovom slučaju broj m se bira iz uslova da rezultirajuća jednačina, ako je moguće, postane homogena do nekog stepena. Međutim, ako se to ne može učiniti, onda se razmatrana DE ne može na ovaj način svesti na homogenu.

Primjer 4 Riješi DE. (18)

Rješenje: Pokažimo da je DE (18) reduciran na homogeni DE upotrebom supstitucije (17) i dalje integrisan korišćenjem supstitucije (3):

Hajde da nađemo sa:

Dakle, određeno rješenje DE (24) ima oblik

.
Diferencijalne jednadžbe.

§ 1. Osnovni pojmovi o običnim diferencijalnim jednačinama.

Definicija 1. Obična diferencijalna jednadžba n– . red za funkciju y argument x naziva se relacija oblika

Gdje F– data funkcija njegovih argumenata. U nazivu ove klase matematičkih jednadžbi, izraz "diferencijalni" naglašava da one uključuju derivate
(funkcije nastale kao rezultat diferencijacije); izraz “običan” označava da željena funkcija zavisi samo od jednog realnog argumenta.

Obična diferencijalna jednadžba možda ne sadrži eksplicitan argument x, traženu funkciju
i bilo koji od njegovih derivata, ali najviši derivat
mora biti uključeno u jednačinu n- th order. Na primjer

A)
– jednačina prvog reda;

b)
– jednačina trećeg reda.

Prilikom pisanja običnih diferencijalnih jednadžbi često se koristi notacija za derivacije u terminima diferencijala:

V)
– jednačina drugog reda;

G)
– jednačina prvog reda,

generator nakon podjele po dx ekvivalentan oblik specificiranja jednadžbe:
.

Funkcija
naziva se rješenjem obične diferencijalne jednadžbe ako se nakon zamjene u nju pretvori u identitet.

Na primjer, jednačina 3. reda

Ima rješenje
.

Pronalaženje jednom ili drugom metodom, na primjer, selekcijom, jedne funkcije koja zadovoljava jednačinu ne znači njeno rješavanje. Riješiti običnu diferencijalnu jednačinu znači pronaći Sve funkcije koje formiraju identitet kada se zamijene u jednadžbu. Za jednadžbu (1.1), familija takvih funkcija se formira pomoću proizvoljnih konstanti i naziva se općim rješenjem obične diferencijalne jednadžbe n-ti red, a broj konstanti se poklapa sa redoslijedom jednadžbe: Opće rješenje može biti, ali nije eksplicitno riješeno u odnosu na y(x) : U ovom slučaju, rješenje se obično naziva općim integralom jednačine (1.1).

Na primjer, opće rješenje diferencijalne jednadžbe
je sljedeći izraz: , a drugi član se također može napisati kao
, budući da je proizvoljna konstanta , podijeljeno sa 2, može se zamijeniti novom proizvoljnom konstantom .

Dodeljivanjem nekih dozvoljenih vrednosti svim proizvoljnim konstantama u opštem rešenju ili u opštem integralu, dobijamo određenu funkciju koja više ne sadrži proizvoljne konstante. Ova funkcija se naziva parcijalno rješenje ili parcijalni integral jednadžbe (1.1). Za pronalaženje vrijednosti proizvoljnih konstanti, a samim tim i određenog rješenja, koriste se različiti dodatni uvjeti za jednadžbu (1.1). Na primjer, takozvani početni uslovi mogu se specificirati u (1.2)

Na desnoj strani početnih uslova (1.2) navedene su numeričke vrednosti funkcije i derivacija, a ukupan broj početnih uslova jednak je broju definisanih proizvoljnih konstanti.

Problem pronalaženja određenog rješenja jednačine (1.1) na osnovu početnih uslova naziva se Cauchyjev problem.

§ 2. Obične diferencijalne jednačine 1. reda - osnovni pojmovi.

Obična diferencijalna jednadžba 1. reda ( n=1) ima oblik:
ili, ako se može riješiti u odnosu na derivat:
. Zajednička odluka y= y(x,SA) ili opšti integral
Jednačine 1. reda sadrže jednu proizvoljnu konstantu. Jedini početni uslov za jednačinu 1. reda
omogućava vam da odredite vrijednost konstante iz općeg rješenja ili iz općeg integrala. Tako će se naći određeno rješenje ili, što je isto, Cauchyjev problem će biti riješen. Pitanje postojanja i jedinstvenosti rješenja Cauchyjevog problema jedno je od centralnih u općoj teoriji običnih diferencijalnih jednadžbi. Za jednačinu 1. reda, posebno, vrijedi teorema, koja je ovdje prihvaćena bez dokaza.

Teorema 2.1. Ako je u jednadžbi funkcija
i njegov parcijalni izvod
kontinuirano u nekom regionu D avion XOY, a u ovoj oblasti je određena tačka
, tada postoji jedinstveno rješenje koje zadovoljava i jednadžbu i početni uvjet
.

Geometrijski, opšte rješenje jednačine 1. reda je porodica krivulja na ravni XOY, koji nemaju zajedničkih tačaka i međusobno se razlikuju po jednom parametru - vrijednosti konstante C. Ove krive se nazivaju integralne krive za datu jednačinu. Krive integralne jednadžbe imaju očigledno geometrijsko svojstvo: u svakoj tački tangenta tangente na krivulju jednaka je vrijednosti desne strane jednačine u toj tački:
. Drugim riječima, jednačina je data u ravni XOY polje pravaca tangenti na integralne krive. komentar: Treba napomenuti da je jednadžba.
jednadžba i takozvana jednačina su date u simetričnom obliku
.

§ 3. Diferencijalne jednačine 1. reda sa odvojivim varijablama.

Definicija. Diferencijalna jednadžba sa odvojivim varijablama je jednadžba oblika
(3.1)

ili jednačina oblika (3.2)

Da bi se odvojile varijable u jednačini (3.1), tj. svesti ovu jednačinu na takozvanu jednačinu odvojene varijable, uradite sljedeće:

;

Sada treba da rešimo jednačinu g(y)= 0 . Ako ima pravo rješenje y= a, To y= aće također biti rješenje jednačine (3.1).

Jednačina (3.2) se svodi na odvojenu promjenljivu jednačinu dijeljenjem sa proizvodom
:

, što nam omogućava da dobijemo opšti integral jednačine (3.2):
. (3.3)

Integralne krive (3.3) će biti dopunjene rješenjima
, ako takva rješenja postoje.

Riješite jednačinu: .

Odvajamo varijable:

Integrisanje, dobijamo

Dalje od jednačina
I
mi nalazimo x=1, y=-1. Ova rješenja su privatna rješenja.

§ 4. Homogene diferencijalne jednačine 1. reda.

Definicija 1. Jednačina 1. reda naziva se homogenom ako je za njenu desnu stranu za bilo koju
odnos je validan
, nazvan uslov homogenosti funkcije dvije varijable nulte dimenzije.

Primjer 1. Pokažite tu funkciju
- homogena nulta dimenzija.

Rješenje.

Q.E.D.

Teorema. Bilo koja funkcija
- homogena i, obrnuto, svaka homogena funkcija
nulta dimenzija se svodi na formu
.

Dokaz.

Prva izjava teoreme je očigledna, jer
. Dokažimo drugu tvrdnju. Hajde da stavimo
, zatim za homogenu funkciju
, što je trebalo dokazati.

Definicija 2. Jednadžba (4.1)

u kojem M I N– homogene funkcije istog stepena, tj. imati imovinu za sve , naziva se homogenim.

Očigledno, ova jednačina se uvijek može svesti na oblik
(4.2), iako da biste ga riješili, ne morate to učiniti.

Homogena jednadžba se svodi na jednadžbu s odvojivim varijablama zamjenom željene funkcije y prema formuli y= zx, Gdje z(x) – nova potrebna funkcija. Nakon što smo izvršili ovu zamjenu u jednačini (4.2), dobijamo:
ili
ili
.

Integracijom dobijamo opšti integral jednačine u odnosu na funkciju z(x)
, koji nakon ponovljene zamjene
daje opšti integral originalne jednačine. Štaviše, ako - korijeni jednadžbe
, zatim funkcije
- rješavanje date homogene jednadžbe. Ako
, tada jednačina (4.2) poprima oblik

i postaje jednačina sa odvojivim varijablama. Njegova rješenja su poludirektna:
.

Komentar. Ponekad je preporučljivo koristiti zamjenu umjesto gornje zamjene x= zy.

§ 5. Diferencijalne jednačine svedene na homogene.

Razmotrimo jednačinu oblika
. (5.1)

Ako
, onda je ovo jednadžba koja koristi supstituciju, gdje I - nove varijable, i - neki konstantni brojevi određeni iz sistema

Svedeno na homogenu jednačinu

Ako
, tada jednačina (5.1) poprima oblik

Believing z= sjekira+ by, dolazimo do jednačine koja ne sadrži nezavisnu varijablu.

Pogledajmo primjere.

Primjer 1.

Integrirajte jednačinu

i istaći integralnu krivu koja prolazi kroz tačke: a) (2;2); b) (1;-1).

Rješenje.

Hajde da stavimo y= zx. Onda dy= xdz+ zdx I

Hajde da ga skratimo i okupljaju članove na dx I dz:

Odvojimo varijable:

.

Integrirajući, dobijamo ;

ili
,
.

Zamjena ovdje z on , dobijamo opšti integral date jednačine u obliku (5.2)
ili

.

Ovo je porodica krugova
, čiji centri leže na pravoj liniji y = x a koji su u početku tangenti na pravu y + x = 0. Ova linijay = - x zauzvrat, određeno rješenje jednačine.

Sada način Cauchyjevog problema:

A) Stavljanje u opšti integral x=2, y=2, mi nalazimo C=2, stoga će traženo rješenje biti
.

B) nijedan krug (5.2) ne prolazi kroz tačku (1;-1). Ali to je poluravno y = - x,
prolazi kroz tačku i daje traženo rješenje.

Primjer 2. Riješite jednačinu: .

Rješenje.

Jednačina je poseban slučaj jednačine (5.1).

Odrednica
u ovom primjeru
, pa moramo riješiti sljedeći sistem

Rešavanje, dobijamo to
. Izvođenjem zamjene u datoj jednačini
, dobijamo homogenu jednačinu. Integracija pomoću zamjene
, mi nalazimo
.

Vraćanje na stare varijable x I y prema formulama
, imamo .

§ 6. Generalizovana homogena jednačina.

Jednačina M(x, y) dx+ N(x, y) dy=0 naziva se generalizirani homogen ako je moguće odabrati takav broj k, da lijeva strana ove jednačine postaje homogena funkcija nekog stepena m relativno x, y, dx I dy pod uslovom da x smatra se vrijednošću prve dimenzije, y – k th merenja , dx I dy – odnosno nula i (k-1) th merenja. Na primjer, ovo bi bila jednadžba
. (6.1)

Vrijedi pod pretpostavkama napravljenim u vezi mjerenja

x, y, dx I dy pripadnici leve strane
I dyće imati dimenzije -2, 2 respektivno k I k-1. Izjednačavajući ih, dobijamo uslov koji traženi broj mora da zadovolji k: -2 = 2k=k-1. Ovaj uslov je zadovoljen kada k= -1 (sa ovim k svi članovi na lijevoj strani jednačine koja se razmatra imat će dimenziju -2). Prema tome, jednačina (6.1) je generalizovana homogena.

Integrirajući ga, nalazimo
, gdje
. Ovo je opšte rješenje jednačine (6.1).

§ 7. Linearne diferencijalne jednačine 1. reda.

Linearna jednačina 1. reda je jednačina koja je linearna u odnosu na željenu funkciju i njen izvod. Izgleda:

, (7.1)

Gdje P(x) I Q(x) – date kontinuirane funkcije od x. Ako je funkcija
, tada jednačina (7.1) ima oblik:
(7.2)

i inače se naziva linearna homogena jednačina
naziva se linearna nehomogena jednačina.

Linearna homogena diferencijalna jednadžba (7.2) je jednadžba sa odvojivim varijablama:

(7.3)

Zamjenom pronađenog izvoda u jednačinu (7.1) imat ćemo:

ili
.

Gdje
, gdje je proizvoljna konstanta. Kao rezultat, opće rješenje nehomogene linearne jednačine (7.1) će biti (7.4)

Kombinirajmo, na primjer, drugi i treći član posljednjeg izraza i izdvojimo funkciju u(x) iza zagrade:
(7.5)

Zahtijevamo da se zagrada poništi:
.

Rešimo ovu jednačinu postavljanjem proizvoljne konstante C jednako nuli:
. Sa pronađenom funkcijom v(x) Vratimo se na jednačinu (7.5):
.

Rešavajući to, dobijamo:
.

Stoga, opće rješenje jednačine (7.1) ima oblik:

§ 8. Bernulijeva jednačina.

Definicija.

Diferencijalna jednadžba oblika
, Gdje
, naziva se Bernoullijeva jednačina.

Pod pretpostavkom da
, podijelite obje strane Bernoullijeve jednadžbe sa . Kao rezultat dobijamo:
(8.1)

Hajde da predstavimo novu funkciju
. Onda
. Pomnožimo jednačinu (8.1) sa
i idemo na funkciju z(x) :
, tj. za funkciju z(x) dobio linearnu nehomogenu jednačinu 1. reda. Ova jednačina se rješava korištenjem metoda o kojima se govori u prethodnom pasusu. Zamijenimo u njegovo opšte rješenje z(x) izraz
, dobijamo opšti integral Bernulijeve jednačine, koji se lako rešava u odnosu na y. At
dodaje se rastvor y(x)=0 . Bernoullijeva jednačina se također može riješiti bez prijelaza na linearnu jednačinu zamjenom
, i korištenjem Bernoullijeve metode, o kojoj se detaljno govori u § 7. Razmotrimo korištenje ove metode za rješavanje Bernoullijeve jednadžbe na konkretnom primjeru.

Primjer. Pronađite opšte rješenje jednačine:
(8.2)

Rješenje.

Stoga, opće rješenje ove jednačine ima oblik:
, y(x)=0.

§ 9. Diferencijalne jednačine u totalnim diferencijalima.

Definicija. Ako u jednadžbi M(x, y) dx+ N(x, y) dy=0 (9.1) lijeva strana je ukupni diferencijal neke funkcije U(x, y) , tada se naziva totalna diferencijalna jednadžba. Ova jednačina se može prepisati kao du(x, y)=0 , dakle, njen opšti integral je u(x, y)= c.

Na primjer, jednadžba xdy+ ydx=0 postoji jednadžba u totalnim diferencijalima, jer se može prepisati u obliku d(xy)=0. Opšti integral će biti xy= c- proizvoljna diferencibilna funkcija. Izdiferencirajmo (9.3) s obzirom na u
§ 10. Integrirajući faktor.

Ako je jednadžba M(x, y) dx + N(x, y) dy = 0 nije totalna diferencijalna jednadžba i postoji funkcija µ = µ(x, y) , tako da nakon množenja obje strane jednačine s njim, dobijamo jednačinu

µ(Mdx + Ndy) = 0 u totalnim diferencijalima, tj. µ(Mdx + Ndy)du, zatim funkciju µ(x, y) naziva se integrirajući faktor jednačine. U slučaju kada je jednadžba već jednačina u totalnim diferencijalima, pretpostavljamo µ = 1.

Ako se pronađe integrirajući faktor µ , tada se integracija ove jednadžbe svodi na množenje obje njene strane sa µ i pronalaženje opšteg integrala rezultirajuće jednačine u totalnim diferencijalima.

Ako µ je kontinuirano diferencibilna funkcija od x I y, To
.

Iz toga slijedi da je integrirajući faktor µ zadovoljava sljedeću parcijalnu diferencijalnu jednačinu 1. reda:

(10.1).

Ako se unapred zna da µ= µ(ω) , Gdje ω – data funkcija iz x I y, tada se jednadžba (10.1) svodi na običnu (i, osim toga, linearnu) jednadžbu s nepoznatom funkcijom µ na nezavisnu varijablu ω :

(10.2),

Gdje
, tj. razlomak je funkcija samo od ω .

Rješavajući jednačinu (10.2), nalazimo integrirajući faktor

, With = 1.

Konkretno, jednačina M(x, y) dx + N(x, y) dy = 0 ima faktor integracije koji zavisi samo od x(ω = x) ili samo od y(ω = y), ako su u skladu sa tim ispunjeni sljedeći uslovi:

,
.

Klikom na dugme "Preuzmi arhivu" potpuno besplatno preuzimate datoteku koja vam je potrebna.
Prije nego što preuzmete ovu datoteku, razmislite o onim dobrim esejima, testovima, seminarskim radovima, disertacijama, člancima i drugim dokumentima koji se ne traže na vašem računalu. Ovo je vaš rad, on treba da učestvuje u razvoju društva i da koristi ljudima. Pronađite ove radove i pošaljite ih u bazu znanja.
Mi i svi studenti, postdiplomci, mladi naučnici koji koriste bazu znanja u svom studiranju i radu bićemo vam veoma zahvalni.

Da preuzmete arhivu sa dokumentom, unesite petocifreni broj u polje ispod i kliknite na dugme "Preuzmi arhivu"

Slični dokumenti

Cauchy problemi za diferencijalne jednadžbe. Grafikon rješenja diferencijalne jednadžbe prvog reda. Jednačine sa odvojivim varijablama i svođenje na homogenu jednačinu. Homogene i nehomogene linearne jednadžbe prvog reda. Bernoullijeva jednačina.

predavanje, dodano 18.08.2012

Osnovni pojmovi teorije običnih diferencijalnih jednadžbi. Predznak jednadžbe u totalnim diferencijalima, konstrukcija općeg integrala. Najjednostavniji slučajevi pronalaženja integrirajućeg faktora. Slučaj množitelja koji zavisi samo od X i samo od Y.

kurs, dodan 24.12.2014

Osobine diferencijalnih jednadžbi kao odnosa između funkcija i njihovih izvoda. Dokaz teoreme postojanja i jedinstvenosti rješenja. Primjeri i algoritam za rješavanje jednadžbi u totalnim diferencijalima. Integrirajući faktor u primjerima.

kurs, dodan 11.02.2014

Riccati diferencijalne jednadžbe. Opće rješenje linearne jednačine. Pronalaženje svih mogućih rješenja Bernoullijeve diferencijalne jednadžbe. Rješavanje jednadžbi sa odvojivim varijablama. Opća i specijalna rješenja Clairautove diferencijalne jednadžbe.

kurs, dodato 26.01.2015

Jednadžba sa odvojivim varijablama. Homogene i linearne diferencijalne jednadžbe. Geometrijska svojstva integralnih krivulja. Potpuni diferencijal funkcije dvije varijable. Određivanje integrala Bernoullijevim metodama i varijacije proizvoljne konstante.

sažetak, dodan 24.08.2015

Pojmovi i rješenja najjednostavnijih diferencijalnih jednadžbi i diferencijalnih jednadžbi proizvoljnog reda, uključujući i one sa konstantnim analitičkim koeficijentima. Sistemi linearnih jednačina. Asimptotičko ponašanje rješenja nekih linearnih sistema.

teza, dodana 10.06.2010

Opšti integral jednadžbe, primjena Lagrangeove metode za rješavanje nehomogene linearne jednadžbe s nepoznatom funkcijom. Rješavanje diferencijalne jednadžbe u parametarskom obliku. Ojlerov uslov, jednačina prvog reda u totalnim diferencijalima.

test, dodano 11.02.2011