Određivanje preseka prave i ravni. Naučna elektronska biblioteka. Posebni slučajevi međusobnog paralelizma i okomitosti prave i ravni. specijalni slučajevi međusobne okomitosti dvije ravni

Linija preseka dve ravni je prava linija. Razmotrimo prvo poseban slučaj (slika 3.9), kada je jedna od ravnina koja se seku paralelna sa horizontalnom ravninom projekcija (α π 1, f 0 α X). U ovom slučaju, linija ukrštanja a, koji pripada avionuα, takođe će biti paralelna sa ravninom π 1, (slika 3.9. a), tj. poklapaće se sa horizontalom ravnina koje se seku (a ≡ h).

Ako je jedna od ravni paralelna sa frontalnom ravninom projekcija (slika 3.9. b), tada će presečna linija a koja pripada ovoj ravni biti paralelna sa ravninom π 2 i poklopit će se s frontalom ravnina koje se sijeku (a ≡ f).

.

.

Rice. 3.9. Poseban slučaj presek ravni opšteg položaja sa ravnima: a - horizontalni nivo; b - frontalni nivo

Primer konstruisanja tačke preseka (K) prave linije a (AB) sa ravninom α (DEF) prikazan je na Sl. 3.10. Da bi se to uradilo, prava linija a je zatvorena u proizvoljnu ravan β i određena je presečna linija ravni α i β.

U primjeru koji razmatramo, prave AB i MN pripadaju istoj ravni β i sijeku se u tački K, a pošto prava MN pripada datoj ravni α (DEF), tačka K je i tačka preseka prave a (AB) sa ravninom α. (Sl. 3.11).

.

Rice. 3.10. Konstruisanje tačke preseka prave i ravni

Da biste riješili takav problem u složenom crtežu, morate biti u stanju pronaći točku presjeka prave linije u općem položaju s ravninom u općem položaju.

Razmotrimo primjer pronalaženja tačke preseka prave linije AB sa ravninom trougla DEF prikazanog na Sl. 3.11.

Za pronalaženje tačke preseka kroz frontalnu projekciju prave A 2 B 2, nacrtana je frontalno projektovana ravan β koja je presecala trougao u tačkama M i N. Na frontalnoj projekcijskoj ravni (π 2) ove tačke su predstavljene projekcijama M 2, N 2. Iz uslova pripadnosti pravoj ravni na horizontalnu ravan projekcija (π 1) nalaze se horizontalne projekcije rezultujućih tačaka M 1 N 1. Na presjeku horizontalnih projekcija pravih A 1 B 1 i M 1 N 1 formira se horizontalna projekcija njihove presječne točke (K 1). Prema liniji komunikacije i uslovima pripadnosti na frontalnoj ravni projekcija nalazi se frontalna projekcija presečne tačke (K 2).

.

Rice. 3.11. Primjer određivanja točke presjeka prave i ravni

Vidljivost segmenta AB u odnosu na trougao DEF određuje se metodom konkurentske tačke.

Na ravni π 2 razmatraju se dvije tačke NEF i 1AB. Iz horizontalnih projekcija ovih tačaka može se ustanoviti da se tačka N nalazi bliže posmatraču (Y N >Y 1) nego tačka 1 (smer vidne linije je paralelan sa S). Posljedično, pravac AB, odnosno dio prave AB (K 1) pokriven je ravninom DEF na ravni π 2 (njena projekcija K 2 1 2 prikazana je isprekidanom linijom). Slično se uspostavlja i vidljivost u ravni π 1.

Pitanja za samokontrolu

1) Koja je suština metode konkurentne tačke?

2) Koja svojstva prave linije znate?

3) Koji je algoritam za određivanje tačke preseka prave i ravni?

4) Koji zadaci se nazivaju pozicioni?

5) Formulirajte uslove za pripadnost pravoj ravni.

Predstavljamo Vam časopise koje izdaje izdavačka kuća "Akademija prirodnih nauka"

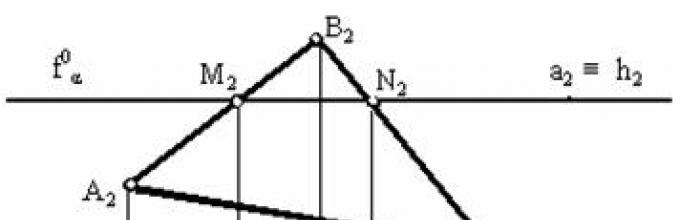
Poznato je da prava siječe ravan ako ne pripada ovoj ravni i nije joj paralelna. Prateći donji algoritam, nalazimo tačku preseka linije a sa generičkom ravninom α definisanom tragovima h 0α , f 0α .

Algoritam

1. Preko direktnog a crtamo pomoćnu frontalno projektovanu ravan γ. Na slici su prikazani njegovi tragovi h 0γ, f 0γ.
2. Konstruišemo projekcije prave AB duž koje se sijeku ravni α i γ. U ovom zadatku, tačka B" = h 0α ∩ h 0γ, A"" = f 0α ∩ f 0γ. Tačke A" i B"" leže na x-osi, njihov položaj je određen komunikacionim linijama.
3. Direktno a i AB seku u željenoj tački K. Njegova horizontalna projekcija K" = a" ∩ A"B". Frontalna projekcija K"" leži na pravoj a"".

Algoritam rješenja će ostati isti ako pl. α će se dati paralelnim linijama koje se ukrštaju, presjekom figure ili drugim mogućim načinom.

Vidljivost linije a u odnosu na ravan α. Metoda konkurentskih bodova

1. Označimo frontalno konkurentne tačke A i C na crtežu (sl. ispod). Pretpostavićemo da tačka A pripada području. α, a C leži na pravoj a. Frontalne projekcije A"" i C"" se poklapaju, ali se istovremeno tačke A i C uklanjaju iz ravnine projekcija P 2 na različitim udaljenostima.
2. Nađimo horizontalne projekcije A" i C". Kao što se vidi na slici, tačka C" je udaljena od ravni P 2 na većoj udaljenosti od tačke A" koja pripada kvadratu. α. Posljedično, bit će vidljiv dio prave linije a"", koji se nalazi lijevo od tačke K"". Sekcija a"" desno od K"" je nevidljiva. Označavamo ga isprekidanom linijom.
3. Označimo na crtežu horizontalno konkurentne tačke D i E. Pretpostavićemo da tačka D pripada kvadratu. α, a E leži na pravoj a. Horizontalne projekcije D" i E" se poklapaju, ali su istovremeno tačke D i E udaljene od ravni P 1 na različitim udaljenostima.
4. Odredimo položaj frontalnih projekcija D"" i E"". Kao što se vidi na slici, tačka D"", koja se nalazi u kvadratu. α, udaljena je od ravni P 1 na većoj udaljenosti od tačke E "", koja pripada pravoj liniji a. Prema tome, dio a" koji se nalazi desno od tačke K" će biti nevidljiv. Označavamo ga isprekidanom linijom. Vidi se dio a" lijevo od K".

Zadana je prava linija: (1) i ravan: Ax + By + Cz + D = 0 (2).

Nađimo koordinate tačke preseka prave i ravni. Ako se prava linija (1) i ravan (2) sijeku, tada koordinate točke presjeka zadovoljavaju jednačine (1) i (2):

, .

Zamjenom pronađene vrijednosti t u (1) dobijamo koordinate tačke preseka.

1) Ako je Am + Bn + Cp = 0, a Ax 0 + By 0 + Cz 0 + D ≠ 0, onda t ne postoji, tj. prava linija i ravan nemaju jednu zajedničku tačku. Oni su paralelni.

2) Am + Bn + Cp = 0 i Ax 0 + By 0 + Cz 0 + D = 0. U ovom slučaju, t može imati bilo koje vrijednosti i , tj. prava je paralelna sa ravninom i ima zajednička tačka, tj. leži u ravni.

Primjer 1. Pronađite tačku sjecišta prave sa ravninom 3x – 3y + 2z – 5 = 0.

3(2t – 1) – 3(4t + 3) + 2 3t – 5 = 0 => -17=0, što je nemoguće za bilo koji t, tj. prava linija i ravan se ne seku.

Primjer 2. Pronađite tačku sjecišta prave i ravni: x + 2y – 4z + 1 = 0.

8t + 13 + 2(2t + 1) – 4(3t + 4) + 1 = 0, 0 + 0 = 0. Ovo vrijedi za bilo koju vrijednost t, tj. prava linija leži u ravni.

Primjer 3. Pronađite tačku sjecišta prave i ravan 3x – y + 2z – 5 = 0.

3(5t + 7) – t – 4 + 2(4t + 5) – 5 = 0, 22t + 22 = 0, t = -1, x = 5(-1) + 7 = 2, y = -1 + 4 = 3, z = 4(-1) + 5 = 1, M(2, 3, 1) – tačka preseka prave i ravni.

Ugao između prave i ravni. Uslovi za paralelnost i okomitost prave i ravni.

Ugao između prave i ravni se naziva oštri ugao q između prave i njene projekcije na ravan.

Neka su date prava i ravan:

i .

Neka prava siječe ravan i sa njom formira ugao μ (). Tada je b = 90 0 – q ili b = 90 0 + q ugao između vektora normale ravni i usmjeravajućeg vektora prave. Ali . Sredstva

(3).

a) Ako je L P, onda - uslov okomitosti prave i ravni.

b) Ako je L||P, onda je uslov paralelnosti prave i ravni.

c) Ako je prava L||P i istovremeno tačka M0(x0, y0, z0) P, tada prava leži u ovoj ravni. analitički:

- uslovi pripadnosti pravoj liniji i ravni.

Primjer. Zadata ravna linija i tačka M 0 (1, 0, –2). Kroz tačku M 0 povući ravan okomitu na ovu pravu. Tražimo jednačinu željene ravni u obliku: A(x – 1) + B(y – 0) + C(z + 2) = 0. U ovom slučaju , ,

5(x – 1) – 5y + 5(z + 2) = 0, - x – y + z + 3 = 0.

Gomila aviona.

Greda ravnina je skup svih ravnina koje prolaze kroz datu pravu liniju – os grede.

Za definiranje snopa ravnina dovoljno je navesti njegovu os. Neka jednačina ove linije bude data u opštem obliku:

.

Sastaviti jednadžbu grede znači sastaviti jednačinu iz koje se može dobiti dodatni uslov jednadžba bilo koje ravni grede, osim b.m. jedan. Pomnožimo jednačinu II sa l i dodajmo je jednačini I:

A 1 x + B 1 y + C 1 z + D 1 + l(A 2 x + B 2 y + C 2 z + D 2) = 0 (1) ili

(A 1 + lA 2)x + (B 1 + lB 2)y + (C 1 + lC 2)z + (D 1 + lD 2) = 0 (2).

l – parametar – broj koji može uzeti realne vrijednosti. Za bilo koju odabranu vrijednost l, jednadžbe (1) i (2) su linearne, tj. ovo su jednadžbe određene ravni.

1. Pokažimo da ova ravan prolazi kroz os grede L. Uzmimo proizvoljnu tačku M 0 (x 0, y 0, z 0) L. Prema tome, M 0 P 1 i M 0 P 2. znači:

3x – y + 2z + 9 + 17x + 17z – 51 = 0; 20x – y + 19z – 42 = 0.

Primjer 3 (E). Napišite jednačinu za ravan koja prolazi kroz pravu okomito na ravan x – 2y + z + 5 = 0. ; 3x – 2y + z – 3 + l(x – 2z) = 0; (3 + l)x – 2y + (1 – 2 l)z – 3 = 0; ; ; l = 8; 11x – 2y – 15z – 3 = 0.

77*. Naći tačku preseka prave AB sa ravni definisanom trouglom CDE (slika 75, a).

Rješenje. Kao što je poznato, da bi se pronašla tačka preseka prave sa opštom ravninom, treba povući pomoćnu ravan (R) kroz pravu liniju, konstruisati liniju preseka ove ravni sa datom (1-2) i pronađite

tačka preseka (K) zadate i konstruisane prave. Tačka K je željena tačka preseka prave sa ravninom (slika 75, b). Horizontalna ili frontalna projekcijska ravan se obično koristi kao pomoćna ravan.

Na sl. 75, u c, frontalno projektovana ravan R povučena je kroz pravu AB, njen trag R ϑ se poklapa sa "c". horizont. Trag ravni nije potreban u ovom problemu i stoga nije prikazan.

Konstruišemo liniju preseka ravni R i ravni definisane trouglom CDE (za primer takve konstrukcije vidi problem 67). Konstruisavši liniju 1-2 (slika 75, c), nalazimo njenu tačku preseka sa pravom linijom AB - tačkom K (k, k").

Da biste odredili presjeke prave AB koje će pokrivati ​​trokut, treba koristiti analizu položaja tačaka na linijama koje se sijeku.

Na primjer, tačke 1 i 3 nalaze se na linijama koje se seku (respektivno) ED i AB. Frontalne projekcije ovih tačaka se poklapaju, tj. tačke 1 i 3 su podjednako udaljene od kvadrata. N. Ali njihove udaljenosti od trga. V su različiti: tačka 3 je dalje od kvadrata. V od tačke 1. Dakle, u odnosu na pl. V tačka 3 pokriva tačku 1 (smjer gledanja je označen strelicom S). Shodno tome, prava linija AB prolazi ispred trougla CDE do tačke K. Počevši od tačke K nalevo, prava linija AB je prekrivena trouglom, pa je stoga ovaj deo prave prikazan isprekidanom linijom.

Za identifikaciju nevidljivog područja na horizontu. projekcije prave AB, razmotrimo tačke 4 i 5 koje leže na pravim AB i CD.

Ako pogledamo ove tačke u pravcu s 1, prvo vidimo tačku 5. Tačka 4 je pokrivena tačkom 5. Shodno tome, prava AB na ovom mestu je pokrivena trouglom CDE, a presek njene projekcije od tačke k do tačke 4 treba biti prikazan isprekidanom linijom. U ovom slučaju, tačka K je bila unutar konture trougla CDE.

Ako je relativni položaj elemenata koji se seku različit, moguće je da će tačka K biti izvan trougla (slika 75, d). To znači da prava AB siječe ravan definiranu trouglom CDE izvan konture ovog trougla. AB postaje nevidljiv iza tačke K (lijevo).

78. Nađite tačke preseka prave AB sa plohama piramide (sl. 76). Lica piramide treba smatrati ravnima definisanim trouglovima.

79. Naći tačke preseka prave AB sa plohama prizme (sl. 77). Lica prizme treba smatrati ravnima definisanim paralelnim pravim linijama.

80*. Naći tačke preseka prave AB sa ravninom P (slika 78, a).

Rješenje. Provučemo frontalno projektovanu ravan R kroz pravu AB (slika 78, b) (njegov trag R ϑ se poklapa sa "b") i konstruišemo pravu MN preseka obe ravni - date i povučene kroz AB ( konstrukcija je slična onoj izvedenoj u zadatku 70). Tražena tačka K(k, k") preseka prave AB sa ravninom P nalazi se u tački preseka MN sa AB.

U ovom zadatku vidljivost pravog dijela od tačke A do K je očigledna; međutim, više teški slučajevi vidljivi dio prave linije treba odrediti na osnovu

analiza položaja tačaka. Na primjer, uzimamo tačku 1 (na pravoj AB) i tačku N (na tragu P ϑ). vidimo da se tačka 1 nalazi dalje u odnosu na kvadrat. V od tačke N. Dakle, prava linija AB do tačke K je vidljiva. Iza tačke K, prava linija je prikazana kao isprekidana linija i nevidljiva je. Slično se određuje i vidljivost horizonta. projekcije.

81. Naći tačku preseka prave AB sa ravninom P (sl. 79).

82*. Naći tačku preseka prave AB sa ravninom P (slika 80, a).

Rješenje. Kroz pravu AB povučemo horizontalno projektovanu ravan R (trag R h poklapa se sa ab) i konstruišemo liniju preseka ravnina P i R,

koristeći tačke M i N preseka njihovih istoimenih koloseka (sl. 80, b i c). Željena tačka (k", k) nalazi se u tački preseka MN sa AB. Na slici 80, d, tačka K je konstruisana pomoću dijagrama W. Pošto je grafika P profilisana (sl. 80, b).

tada projekcija profila k" leži u tački preseka traga P ω sa a"b". Znajući k", konstruišemo k" na a"b" i k na ab. Vidljivi preseci prave AB su određeno na isti način kao u zadacima 77 i 80.

83. Naći tačku preseka prave AB sa ravni P (slika 81).

84*. Naći tačku preseka prave AB sa ravni definisanom trouglom CDE (slika 82, a).

Rješenje. Kroz pravu AB crtamo (sl. 82, b i c) kvadrat. R, paralelno sa kvadratom W. Ona prelazi dati avion duž prave MN (tačke m, n", m i n leže na presjeku tragova R ϑ i R h sa istim projekcijama odgovarajućih stranica

trougao CDE). Kako su prave AB i MN profilne, onda da bismo pronašli tačku (K) njihovog presjeka konstruiramo projekcije profila a"b" i m"n". Projekcija k" nalazi se na preseku a"b" i m"m". Koristeći k" konstruišemo k" na a"b" i k na ab.

85. Naći tačku preseka prave EF sa ravni definisanom četvorouglom ABCD (slika 83).