“Crteži za slajdove” - Izborni predmet “Svijet multimedijalnih tehnologija”. Crteži na slajdovima. C) možete prenijeti crtež tako što ćete uhvatiti sredinu mišem. Umetanje slika na slajd. Općinski obrazovne ustanove prosjek sveobuhvatne škole Br. 5. 95% informacija osoba percipira preko organa vida...
“Funkcije i njihovi grafovi” - 3. Tangentna funkcija. Trigonometrijski. Funkcija je definirana i kontinuirana preko cijelog skupa realnih brojeva. definicija: Numerička funkcija, dato formulom y = cos x, naziva se kosinus. 4.Kotangentna funkcija. U tački x = a funkcija može ili ne mora postojati. Definicija 1. Neka je funkcija y = f(x) definirana na intervalu.
"Funkcije nekoliko varijabli" - Najveći i najmanju vrijednost funkcije. Weierstrassova teorema. Unutrašnje i granične tačke. Granica funkcije od 2 varijable. Funkcijski graf. Teorema. Kontinuitet. Ograničeno područje. Otvorene i zatvorene površine. Derivati višeg reda. Parcijalni derivati. Djelomični prirast funkcije od 2 varijable.
“3D crteži na asfaltu” - Kurt je svoje prve radove počeo stvarati sa 16 godina u Santa Barbari, gdje je postao ovisan o uličnoj umjetnosti. 3d crteži na asfaltu. Kurt Wenner je jedan od najpoznatijih uličnih umjetnika koji crta 3D crteže na asfaltu koristeći obične bojice. SAD. Kao mladić, Kurt Wenner je radio kao ilustrator za NASA-u, gdje je kreirao početne slike budućih svemirskih letjelica.
“Funkcija teme” - Ako učenici rade drugačije, onda bi nastavnik trebao raditi s njima drugačije. Potrebno je saznati ne ono što učenik ne zna, već ono što zna. Generalizacija. Sinteza. Rezultati Jedinstvenog državnog ispita matematike. Program izborni predmet. Udruženje. Edukativni i tematski plan (24 sata). Analogija. Ako učenik nadmaši nastavnika, to je učiteljeva sreća.
Svojstva i zadaci grafova kvadratna funkcija uzrokuju, kako praksa pokazuje, ozbiljne poteškoće. Ovo je prilično čudno, jer kvadratnu funkciju proučavaju u 8. razredu, a zatim kroz prvu četvrtinu 9. razreda “muče” svojstva parabole i grade njene grafove za različite parametre.
To je zbog činjenice da kada tjeraju učenike da konstruiraju parabole, oni praktički ne posvećuju vrijeme "čitanju" grafikona, odnosno ne vježbaju razumijevanje informacija dobivenih sa slike. Očigledno se pretpostavlja da će, nakon konstruiranja desetak ili dva grafikona, pametan student sam otkriti i formulirati odnos između koeficijenata u formuli i izgled grafike. U praksi to ne funkcionira. Za takvu generalizaciju potrebno je ozbiljno iskustvo u matematičkim mini istraživanjima, koje većina učenika devetog razreda, naravno, nema. U međuvremenu, Državni inspektorat predlaže utvrđivanje predznaka koeficijenata pomoću rasporeda.
Nećemo zahtijevati nemoguće od školaraca i jednostavno ćemo ponuditi jedan od algoritama za rješavanje takvih problema.
Dakle, funkcija forme y = ax 2 + bx + c naziva se kvadratnim, njegov graf je parabola. Kao što ime govori, glavni pojam je sjekira 2. To je A ne bi trebali biti jednaki nuli, preostali koeficijenti ( b I With) može biti jednaka nuli.
Pogledajmo kako predznaci njegovih koeficijenata utiču na izgled parabole.
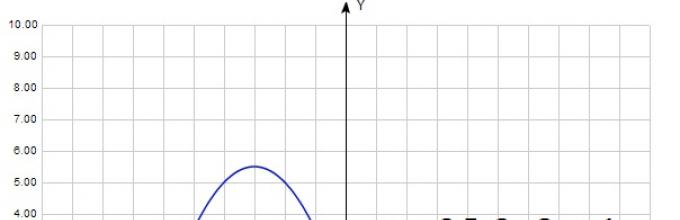
Najjednostavnija zavisnost za koeficijent A. Većina školaraca samouvjereno odgovara: „ako A> 0, tada su grane parabole usmjerene prema gore, i ako A < 0, - то вниз". Совершенно верно. Ниже приведен график квадратичной функции, у которой A > 0.
y = 0,5x 2 - 3x + 1
U ovom slučaju A = 0,5
A sada za A < 0:
y = - 0,5x2 - 3x + 1
U ovom slučaju A = - 0,5

Uticaj koeficijenta With Takođe je prilično lako pratiti. Zamislimo da želimo pronaći vrijednost funkcije u nekoj tački X= 0. Zamijenite nulu u formulu:
y = a 0 2 + b 0 + c = c. Ispostavilo se da y = c. To je With je ordinata tačke preseka parabole sa y-osom. Obično je ovu tačku lako pronaći na grafikonu. I odredite da li leži iznad nule ili ispod. To je With> 0 ili With < 0.
With > 0:
y = x 2 + 4x + 3

With < 0
y = x 2 + 4x - 3

Shodno tome, ako With= 0, tada će parabola nužno proći kroz ishodište:
y = x 2 + 4x

Teže s parametrom b. Tačka u kojoj ćemo je pronaći ne zavisi samo od toga b ali i iz A. Ovo je vrh parabole. Njegova apscisa (koordinata ose X) se nalazi po formuli x in = - b/(2a). dakle, b = - 2ax in. Odnosno, postupimo na sljedeći način: pronađemo vrh parabole na grafu, odredimo predznak njegove apscise, odnosno gledamo desno od nule ( x in> 0) ili lijevo ( x in < 0) она лежит.
Međutim, to nije sve. Takođe moramo obratiti pažnju na predznak koeficijenta A. Odnosno, pogledajte gdje su usmjerene grane parabole. I tek nakon toga, po formuli b = - 2ax in odredi znak b.
Pogledajmo primjer:

Grane su usmjerene prema gore, što znači A> 0, parabola seče osu at ispod nule, tj With < 0, вершина параболы лежит правее нуля. Следовательно, x in> 0. Dakle b = - 2ax in = -++ = -. b < 0. Окончательно имеем: A > 0, b < 0, With < 0.
Linearna funkcija naziva se funkcija forme y = kx + b, definisan na skupu svih realnih brojeva. Evo k– nagib ( pravi broj), b – besplatni član(pravi broj), x- nezavisna varijabla.
U posebnom slučaju, ako k = 0, dobijamo konstantnu funkciju y = b, čiji je graf prava linija paralelna s osi Ox koja prolazi kroz tačku s koordinatama (0; b).
Ako b = 0, tada dobijamo funkciju y = kx, koji je direktnu proporcionalnost.
b – dužina segmenta, koji je odsječen ravnom linijom duž ose Oy, računajući od početka.
Geometrijsko značenje koeficijenta k – ugao nagiba ravno u pozitivnom smjeru ose Ox, posmatrano u smjeru suprotnom od kazaljke na satu.
Svojstva linearne funkcije:
1) Područje definicije linearne funkcije je cijela realna os;
2) Ako k ≠ 0, tada je raspon vrijednosti linearne funkcije cijela realna os. Ako k = 0, tada se raspon vrijednosti linearne funkcije sastoji od broja b;
3) Parnost i neparnost linearne funkcije ovise o vrijednostima koeficijenata k I b.
a) b ≠ 0, k = 0, dakle, y = b – paran;
b) b = 0, k ≠ 0, dakle y = kx – neparan;
c) b ≠ 0, k ≠ 0, dakle y = kx + b – funkcija opšteg oblika;
d) b = 0, k = 0, dakle y = 0 – i parne i neparne funkcije.
4) Linearna funkcija nema svojstvo periodičnosti;
5) Točke preseka sa koordinatnim osa:
vol: y = kx + b = 0, x = -b/k, dakle (-b/k; 0)– tačka preseka sa osom apscise.
oy: y = 0k + b = b, dakle (0; b)– tačka preseka sa ordinatnom osom.
Napomena: Ako b = 0 I k = 0, zatim funkciju y = 0 ide na nulu za bilo koju vrijednost varijable X. Ako b ≠ 0 I k = 0, zatim funkciju y = b ne nestaje ni za jednu vrijednost varijable X.
6) Intervali konstantnosti predznaka zavise od koeficijenta k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b– pozitivno kada x od (-b/k; +∞),
y = kx + b– negativno kada x od (-∞; -b/k).
b) k< 0; kx + b < 0, kx < -b, x < -b/k.
y = kx + b– pozitivno kada x od (-∞; -b/k),
y = kx + b– negativno kada x od (-b/k; +∞).
c) k = 0, b > 0; y = kx + b pozitivno u cijelom rasponu definicija,
k = 0, b< 0; y = kx + b negativan u cijelom rasponu definicija.
7) Intervali monotonosti linearne funkcije zavise od koeficijenta k.
k > 0, dakle y = kx + b povećava se u cijelom domenu definicije,
k< 0 , dakle y = kx + b opada u cijelom domenu definicije.
8) Grafikon linearne funkcije je prava linija. Za konstruisanje prave linije dovoljno je poznavati dve tačke. Položaj prave linije na koordinatnoj ravni ovisi o vrijednostima koeficijenata k I b. Ispod je tabela koja to jasno ilustruje.
Linearna funkcija je funkcija oblika y=kx+b, gdje je x nezavisna varijabla, k i b su bilo koji brojevi.
Grafikon linearne funkcije je prava linija.
1. Izgraditi graf funkcije, potrebne su nam koordinate dvije tačke koje pripadaju grafu funkcije. Da biste ih pronašli, trebate uzeti dvije vrijednosti x, zamijeniti ih u jednadžbu funkcije i koristiti ih za izračunavanje odgovarajućih y vrijednosti.
Na primjer, za crtanje funkcije y= x+2, zgodno je uzeti x=0 i x=3, tada će ordinate ovih tačaka biti jednake y=2 i y=3. Dobijamo tačke A(0;2) i B(3;3). Povežimo ih i dobijemo graf funkcije y= x+2:
2.
U formuli y=kx+b, broj k se naziva koeficijent proporcionalnosti:
ako je k>0, tada funkcija y=kx+b raste
ako k
Koeficijent b pokazuje pomak grafa funkcije duž ose OY:
ako je b>0, tada se graf funkcije y=kx+b dobija iz grafa funkcije y=kx pomicanjem b jedinica prema gore duž ose OY
ako b
Na slici ispod prikazani su grafovi funkcija y=2x+3; y= ½ x+3; y=x+3

Imajte na umu da je u svim ovim funkcijama koeficijent k iznad nule, a funkcije su povećanje.Štaviše, što je veća vrijednost k, veći je ugao nagiba prave linije u pozitivnom smjeru ose OX.
U svim funkcijama b=3 - i vidimo da svi grafovi sijeku osu OY u tački (0;3)
Sada razmotrite grafove funkcija y=-2x+3; y=- ½ x+3; y=-x+3

Ovaj put u svim funkcijama koeficijent k manje od nule i funkcije se smanjuju. Koeficijent b=3, a grafovi, kao iu prethodnom slučaju, sijeku osu OY u tački (0;3)
Razmotrimo grafove funkcija y=2x+3; y=2x; y=2x-3

Sada su u svim jednadžbama funkcije koeficijenti k jednaki 2. I dobili smo tri paralelne prave.
Ali koeficijenti b su različiti, a ovi grafovi sijeku os OY u različitim tačkama:
Grafikon funkcije y=2x+3 (b=3) siječe osu OY u tački (0;3)
Grafikon funkcije y=2x (b=0) siječe osu OY u tački (0;0) - ishodištu.
Grafikon funkcije y=2x-3 (b=-3) siječe osu OY u tački (0;-3)
Dakle, ako znamo predznake koeficijenata k i b, onda možemo odmah zamisliti kako izgleda grafik funkcije y=kx+b.
Ako k 0

Ako k>0 i b>0, tada graf funkcije y=kx+b izgleda ovako:

Ako k>0 i b, tada graf funkcije y=kx+b izgleda ovako:

Ako k, tada grafik funkcije y=kx+b izgleda ovako:

Ako k=0, tada se funkcija y=kx+b pretvara u funkciju y=b i njen graf izgleda ovako:

Ordinate svih tačaka na grafu funkcije y=b jednake su b If b=0, tada graf funkcije y=kx (direktna proporcionalnost) prolazi kroz ishodište:

3. Zabilježimo posebno grafik jednačine x=a. Grafikon ove jednačine je prava linija paralelna sa OY osi, čije sve tačke imaju apscisu x=a.
Na primjer, graf jednadžbe x=3 izgleda ovako:
Pažnja! Jednačina x=a nije funkcija, tako da odgovara jedna vrijednost argumenta različita značenja funkcije, što ne odgovara definiciji funkcije.

4. Uslov za paralelnost dve prave:
Grafikon funkcije y=k 1 x+b 1 je paralelan sa grafikom funkcije y=k 2 x+b 2 ako je k 1 =k 2
5. Uslov da dvije prave budu okomite:
Grafikon funkcije y=k 1 x+b 1 je okomit na grafik funkcije y=k 2 x+b 2 ako je k 1 *k 2 =-1 ili k 1 =-1/k 2
6. Tačke presjeka grafa funkcije y=kx+b sa koordinatnim osa.
Sa OY osom. Apscisa bilo koje tačke koja pripada osi OY jednaka je nuli. Stoga, da biste pronašli točku presjeka sa OY osom, trebate zamijeniti nulu u jednadžbi funkcije umjesto x. Dobijamo y=b. To jest, tačka preseka sa OY osom ima koordinate (0; b).
Sa OX osom: Ordinata bilo koje tačke koja pripada OX osi je nula. Stoga, da biste pronašli točku presjeka sa OX osom, trebate zamijeniti nulu u jednadžbi funkcije umjesto y. Dobijamo 0=kx+b. Dakle, x=-b/k. To jest, tačka preseka sa OX osom ima koordinate (-b/k;0):
5. Monom Umnožak brojčanih i alfabetskih faktora se naziva. Koeficijent naziva se numerički faktor monoma.
6. Da biste napisali monom u standardnom obliku, trebate: 1) Pomnožite brojčane faktore i stavite njihov proizvod na prvo mesto; 2) Pomnožite snage sa po istoj osnovi i stavite rezultirajući proizvod iza brojčanog faktora.
7. Polinom se zove algebarski zbir nekoliko monoma.
8. Da pomnožimo monom polinomom, Morate pomnožiti monom sa svakim članom polinoma i dodati rezultirajuće proizvode.
9. Da pomnožimo polinom sa polinomom, Potrebno je pomnožiti svaki član jednog polinoma sa svakim članom drugog polinoma i dodati dobijene proizvode.
10. Kroz bilo koje dvije tačke možete povući pravu liniju, i to samo jednu.
11. Dvije ravne linije ili imaju samo jednu zajednička tačka, ili nemaju zajedničke tačke.
12. Dvije geometrijske figure nazivaju se jednakim ako se mogu kombinirati preklapanjem.
13. Tačka na segmentu koja ga dijeli na pola, odnosno na dva jednaka segmenta, naziva se sredinom segmenta.
14. Zraka koja izlazi iz vrha ugla i dijeli ga na dva dijela jednakih uglova, naziva se simetrala ugla.
15. Rotirani ugao je 180°.
16. Ugao se naziva pravim ako je jednak 90°.
17. Ugao se naziva oštar ako je manji od 90°, odnosno manji od pravog ugla.
18. Ugao se naziva tupim ako je veći od 90°, ali manji od 180°, odnosno veći od pravog ugla, ali manji od pravog ugla.
19. Dva ugla u kojima je jedna strana zajednička, a druga dva nastavci jedan drugog nazivaju se susjednim.
20. Zbir susjednih uglova je 180°.
21. Dva ugla se nazivaju vertikalnim ako su stranice jednog ugla nastavak stranica drugog.
22. Vertikalni uglovi su jednaki.
23. Dvije prave koje se seku nazivaju se okomite (ili međusobno
okomito) ako tvore četiri prava ugla.
24. Dvije prave okomite na treću se ne sijeku.
25. Faktor polinoma- znači predstaviti ga kao proizvod više monoma i polinoma.
26. Metode faktoringa polinoma:
a) stavljanje zajedničkog faktora iz zagrada,
b) upotreba skraćenih formula za množenje,
c) način grupisanja.
27. Da biste razložili polinom vađenjem zajedničkog faktora iz zagrada, trebate:
a) pronađite ovaj zajednički faktor,
b) izvadi iz zagrada,
c) podijeliti svaki član polinoma ovim faktorom i dodati dobijene rezultate.
Znakovi jednakosti trouglova
1) Ako su dvije stranice i ugao između njih jednog trougla, respektivno, jednaki dvjema stranicama i kutu između njih drugog trougla, onda su takvi trouglovi podudarni.
2) Ako su stranica i dva susedna ugla jednog trougla, respektivno, jednaki strani i dva susedna ugla drugog trougla, onda su takvi trouglovi podudarni.
3) Ako su tri strane jednog trougla respektivno jednake trima stranicama drugog trougla, onda su ti trouglovi podudarni.
1. Faktorizacija korištenjem skraćenih formula za množenje:
a 2 – b 2 = (a – b) (a + b)
a 3 – b 3 = (a – b) (a 2 + ab + b 2)
a 3 + b 3 = (a + b) (a 2 – ab + b 2)
2. Skraćene formule za množenje:
(a + b) 2 =a 2 + 2ab + b 2
(a – b) 2 = a 2 – 2ab + b 2
(a + b) 3 =a 3 + 3a 2 b + 3ab 2 + b 3
(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3
3. Segment koji povezuje vrh trougla sa sredinom suprotne strane naziva se medijana trougao.
4. Okomita povučena iz vrha trougla na pravu koja sadrži suprotnu stranu naziva se visina trougao.
5. IN jednakokraki trougao uglovi u osnovi su jednaki.
6. U jednakokračnom trouglu, simetrala povučena do osnove je medijan i visina.
7. Obim pozvao geometrijska figura, koji se sastoji od svih tačaka ravnine koje se nalaze na datoj udaljenosti od ove tačke.
8. Segment koji povezuje centar sa bilo kojom tačkom na kružnici naziva se radijus krug .
9. Segment koji spaja dvije tačke na kružnici naziva se akord.
Zove se tetiva koja prolazi središtem kružnice prečnika
10. Direktna proporcionalnost y = kx , Gdje X - nezavisna varijabla, To – broj različit od nule ( To – koeficijent proporcionalnosti).
11. Grafikon direktne proporcionalnosti je prava linija koja prolazi kroz početak koordinata.
12. Linearna funkcija je funkcija koja se može dati formulom y = kx + b , Gdje X - nezavisna varijabla, To I b - neki brojevi.
13. Grafikon linearne funkcije- ovo je prava linija.
14 X – argument funkcije (nezavisna varijabla)
at – vrijednost funkcije (zavisna varijabla)
15. At b=0 funkcija poprima oblik y=kx, njegov graf prolazi kroz ishodište.
At k=0 funkcija poprima oblik y=b, njegov graf je horizontalna linija koja prolazi kroz tačku ( 0;b).
Podudarnost između grafika linearne funkcije i predznaka koeficijenata k i b
1. Zovu se dvije prave u ravni paralelno, ako se ne seku.