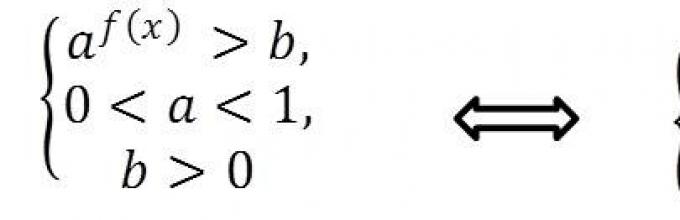Nejednakost je numerički odnos koji ilustruje veličinu brojeva u odnosu jedan na drugi. Nejednakosti se široko koriste u traženju veličina u primijenjenim naukama. Naš kalkulator će vam pomoći da se nosite s tako teškom temom kao što je rješavanje linearne nejednakosti.
Šta je nejednakost
Nejednaki omjeri u pravi zivot korelirati sa stalno poređenje razni objekti: viši ili niži, dalje ili bliže, teži ili lakši. Intuitivno ili vizualno možemo shvatiti da je jedan predmet veći, viši ili teži od drugog, ali u stvari uvijek govorimo o upoređivanju brojeva koji karakteriziraju odgovarajuće veličine. Objekti se mogu porediti po bilo kojoj osnovi iu svakom slučaju možemo stvoriti numeričku nejednakost.
Ako su nepoznate veličine jednake pod određenim uslovima, onda kreiramo jednačinu da ih odredimo numerički. Ako ne, onda umjesto znaka „jednako“ možemo označiti bilo koji drugi odnos između ovih veličina. Dva broja ili matematički objekti mogu biti veći od ">", manji od "<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.
Znakove nejednakosti u njihovom modernom obliku izmislio je britanski matematičar Thomas Harriot, koji je 1631. objavio knjigu o nejednakim omjerima. Znakovi veći od ">" i manji od "<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.
Rješavanje nejednačina
Nejednakosti, kao i jednačine, dolaze u različitim vrstama. Linearni, kvadratni, logaritamski ili eksponencijalni nejednaki odnosi rješavaju se različitim metodama. Međutim, bez obzira na metodu, svaka nejednakost se prvo mora svesti na standardni oblik. Za to se koriste transformacije identiteta koje su identične modifikacijama jednakosti.
Identične transformacije nejednakosti
Takve transformacije izraza su vrlo slične jednadžbama duhova, ali imaju nijanse koje je važno uzeti u obzir prilikom rješavanja nejednačina.
Prva transformacija identiteta je identična sličnoj operaciji s jednakostima. Isti broj ili izraz sa nepoznatim x može se dodati ili oduzeti na obje strane nejednakog odnosa, dok predznak nejednakosti ostaje isti. Najčešće se ova metoda koristi u pojednostavljenom obliku kao prijenos pojmova izraza kroz znak nejednakosti sa promjenom predznaka broja u suprotan. To znači promjenu predznaka samog pojma, odnosno, +R kada se prenese kroz bilo koji znak nejednakosti promijenit će se u – R i obrnuto.
Druga transformacija ima dvije tačke:
- Obje strane nejednakog omjera mogu se pomnožiti ili podijeliti istim pozitivnim brojem. Sam predznak nejednakosti se neće promijeniti.
- Obje strane nejednakosti mogu se podijeliti ili pomnožiti sa istom stvari negativan broj. Sam znak nejednakosti će se promijeniti u suprotno.
Druga identična transformacija nejednačina ima ozbiljne razlike sa modifikacijom jednačina. Prvo, kada se množi/dijeli negativnim brojem, predznak nejednakog izraza je uvijek obrnut. Drugo, dijelove omjera možete podijeliti ili množiti samo brojem, a ne bilo kojim izrazom koji sadrži nepoznatu. Činjenica je da ne možemo sa sigurnošću znati da li je broj veći ili manji od nule skriven iza nepoznatog, pa se druga transformacija identiteta primjenjuje na nejednakosti isključivo s brojevima. Pogledajmo ova pravila s primjerima.
Primjeri oslobađanja nejednakosti
U zadacima iz algebre postoje različiti zadaci na temu nejednakosti. Neka nam bude dat izraz:
6x − 3(4x + 1) > 6.
Prvo, otvorimo zagrade i pomjerimo sve nepoznate ulijevo, a sve brojeve udesno.
6x − 12x > 6 + 3
Moramo podijeliti obje strane izraza sa −6, pa kada pronađemo nepoznato x, predznak nejednakosti će se promijeniti u suprotan.
U rješavanju ove nejednakosti koristili smo oba transformacije identiteta: Pomaknite sve brojeve desno od znaka i podijelite obje strane omjera negativnim brojem.
Naš program je kalkulator za rješavanje numeričkih nejednačina koje ne sadrže nepoznanice. Program sadrži sljedeće teoreme za odnose tri broja:
- ako je A< B то A–C< B–C;
- ako je A > B, onda A–C > B–C.
Umjesto oduzimanja pojmova A-C, možete odrediti bilo koju aritmetičku operaciju: sabiranje, množenje ili dijeljenje. Na ovaj način, kalkulator će automatski prikazati nejednakosti za zbrojeve, razlike, proizvode ili razlomke.
Zaključak
U stvarnom životu, nejednakosti su uobičajene kao i jednačine. Naravno, znanje o rješavanju nejednakosti možda neće biti potrebno u svakodnevnom životu. Međutim, u primijenjenim naukama, nejednakosti i njihovi sistemi se široko koriste. Na primjer, različite studije problema globalne ekonomije svode se na kompilaciju i razdvajanje sistema linearnih ili kvadratne nejednakosti, a neki nejednaki odnosi služe kao nedvosmislen način dokazivanja postojanja određenih objekata. Koristite naše programe za rješavanje linearnih nejednakosti ili provjerite vlastite proračune.
Zdravo! Dragi moji studenti, u ovom članku ćemo naučiti kako riješiti eksponencijalne nejednakosti .
Koliko god vam se eksponencijalna nejednakost činila komplikovanom, nakon nekih transformacija (o njima ćemo malo kasnije) sve nejednakosti svodi se na rješavanje najjednostavnijeg eksponencijalne nejednakosti :
a x > b, sjekira< b I a x ≥ b, a x ≤ b.
Pokušajmo shvatiti kako se takve nejednakosti rješavaju.
Mi ćemo potražiti rješenje stroge nejednakosti. Jedina razlika pri rješavanju nestrogih nejednakosti je u tome što su rezultirajući odgovarajući korijeni uključeni u odgovor.
Pretpostavimo da trebamo riješiti nejednakost oblika i f (x) > b, Gdje a>1 I b>0.
Pogledajte dijagram za rješavanje takvih nejednakosti (slika 1):
Pogledajmo sada konkretan primjer. Riješite nejednačinu: 5 x – 1 > 125.
Pošto je 5 > 1 i 125 > 0, onda
x – 1 > log 5 125, tj
x – 1 > 3,
x > 4.
odgovor: (4; +∞) .
Šta će biti rješenje za ovu istu nejednakost? i f (x) >b, Ako 0
Dakle, dijagram na slici 2

primjer: Riješite nejednakost (1/2) 2x - 2 ≥ 4
Primjenom pravila (slika 2) dobijamo
2h – 2 ≤ log 1/2 4,
2h – 2 ≤ –2,
2x ≤ 0,
x ≤ 0.
odgovor: (–∞; 0] .
Pogledajmo ponovo istu nejednakost i f (x) > b, Ako a>0 I b<0 .
Dakle, dijagram na slici 3:

Primjer rješavanja nejednakosti (1/3) x + 2 > –9. Kao što primjećujemo, bez obzira kojim brojem zamijenimo x, (1/3) x + 2 je uvijek veći od nule.
odgovor: (–∞; +∞) .
Kako se rješavaju nejednakosti oblika? i f(x)< b , Gdje a>1 I b>0?
Dijagram na slici 4:

I sljedeći primjer: 3 3 – x ≥ 8.
Pošto je 3 > 1 i 8 > 0, onda
3 – x > log 3 8, tj
–x > log 3 8 – 3,
X< 3 – log
3 8.
odgovor: (0; 3–log 3 8) .
Kako se rješenje nejednakosti može promijeniti? i f(x)< b
, at 0
Dijagram na slici 5:

I sljedeći primjer: Riješite nejednakost 0,6 2x – 3< 0,36 .
Prateći dijagram na slici 5, dobijamo
2x – 3 > log 0,6 0,36,
2h – 3 > 2,
2x > 5,
x > 2.5
odgovor: (2,5; +∞) .
Razmotrimo posljednju shemu za rješavanje nejednakosti oblika i f(x)< b , at a>0 I b<0 , prikazan na slici 6:

Na primjer, riješimo nejednakost:

Napominjemo da bez obzira kojim brojem zamijenimo x, lijeva strana nejednakosti je uvijek veća od nule, a naš izraz manji od -8, tj. i nula, što znači da nema rješenja.
odgovor: nema rješenja.
Znajući kako riješiti najjednostavnije eksponencijalne nejednakosti, možete nastaviti rješavanje eksponencijalnih nejednačina.
Primjer 1.
Odredite najveću cjelobrojnu vrijednost x koja zadovoljava nejednakost

Budući da je 6 x veće od nule (u svakom slučaju x nazivnik ide na nulu), množenjem obje strane nejednakosti sa 6 x dobivamo:
440 – 2 6 2x > 8, onda
– 2 6 2x > 8 – 440,
– 2 6 2h > – 332,
6 2x< 216,
2x< 3,
x< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.
Odgovor: 1.
Primjer 2.
Riješite nejednakost 2 2 x – 3 2 x + 2 ≤ 0
Označimo 2 x sa y, dobijemo nejednakost y 2 – 3y + 2 ≤ 0 i riješimo ovu kvadratnu nejednakost.
y 2 – 3y +2 = 0,
y 1 = 1 i y 2 = 2.
Grane parabole su usmjerene prema gore, nacrtajmo graf:

Tada će rješenje nejednakosti biti nejednakost 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.
odgovor: (0; 1) .
Primjer 3. Riješite nejednakost 5 x +1 – 3 x +2< 2·5 x – 2·3 x –1
Skupimo izraze sa istim osnovama u jednom dijelu nejednakosti
5 x +1 – 2 5 x< 3 x +2 – 2·3 x –1
Uzmimo 5 x iz zagrada na lijevoj strani nejednakosti, a 3 x na desnoj strani nejednakosti i dobićemo nejednakost
5 x (5 – 2)< 3 х (9 – 2/3),
3·5 x< (25/3)·3 х
Podelite obe strane nejednakosti izrazom 3 3 x, predznak nejednakosti se ne menja, pošto je 3 3 x pozitivan broj, dobijamo nejednakost:


X< 2 (так как 5/3 > 1).
odgovor: (–∞; 2) .
Ako imate pitanja o rješavanju eksponencijalnih nejednačina ili želite vježbati rješavanje sličnih primjera, prijavite se na moje lekcije. Tutor Valentina Galinevskaya.
web stranicu, kada kopirate materijal u cijelosti ili djelomično, link na izvor je obavezan.
Intervalna metoda– jednostavan način za rješavanje frakcionih racionalnih nejednakosti. Ovo je naziv za nejednakosti koje sadrže racionalne (ili frakciono-racionalne) izraze koji zavise od promenljive.
1. Razmotrimo, na primjer, sljedeću nejednakost
Intervalna metoda vam omogućava da to riješite za nekoliko minuta.
Na lijevoj strani ove nejednakosti – frakciona racionalna funkcija. Racionalno jer ne sadrži korijene, sinuse, logaritme - samo racionalni izrazi. Desno je nula.
Intervalna metoda je zasnovana na sljedećem svojstvu razlomke racionalne funkcije.
Razlomka racionalna funkcija može promijeniti predznak samo u onim tačkama u kojima je jednaka nuli ili ne postoji.
Podsjetimo vas kako činiti faktore kvadratni trinom, odnosno izraz oblika .
Gdje i gdje su korijeni kvadratna jednačina.
Crtamo os i stavljamo tačke u kojima brojnik i imenilac idu na nulu.

Nule nazivnika i su probušene tačke, pošto u tim tačkama funkcija na levoj strani nejednakosti nije definisana (ne možete deliti sa nulom). Nule brojioca i - su zasjenjene, jer nejednakost nije stroga. Kada i naša nejednakost je zadovoljena, jer su obje njegove strane jednake nuli.
Ove tačke lome osu na intervale.
Odredimo predznak razlomke racionalne funkcije na lijevoj strani naše nejednakosti na svakom od ovih intervala. Sjećamo se da razlomka racionalna funkcija može promijeniti predznak samo u onim tačkama u kojima je jednaka nuli ili ne postoji. To znači da će u svakom od intervala između tačaka u kojima brojnik ili nazivnik ide na nulu, predznak izraza na lijevoj strani nejednakosti biti konstantan - ili "plus" ili "minus".
I stoga, da bismo odredili predznak funkcije na svakom takvom intervalu, uzimamo bilo koju tačku koja pripada ovom intervalu. Onaj koji nam odgovara.
. Uzmite, na primjer, i provjerite predznak izraza na lijevoj strani nejednakosti. Svaka od "zagrada" je negativna. Na lijevoj strani je znak.

Sljedeći interval: . Provjerimo znak na . Nalazimo da je lijeva strana promijenila svoj znak u .

Hajde da ga uzmemo. Kada je izraz pozitivan - dakle, pozitivan je u cijelom intervalu od do.

Kada je lijeva strana nejednakosti negativna.

I na kraju, class="tex" alt="x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Pronašli smo u kojim intervalima je izraz pozitivan. Ostaje samo da zapišete odgovor:
Odgovor: .
Napomena: znakovi se izmjenjuju između intervala. Ovo se desilo zato što pri prolasku kroz svaku tačku tačno jedan od linearnih faktora je promenio predznak, dok su ostali ostali nepromenjeni.
Vidimo da je metoda intervala vrlo jednostavna. Da bismo riješili frakciono-racionalnu nejednakost metodom intervala, svodimo je na oblik:
Or class="tex" alt="\genfrac())()(0)(\displaystyle P\left(x \right))(\displaystyle Q\left(x \right)) > 0"> !}, ili ili .
(na lijevoj strani je frakciona racionalna funkcija, na desnoj strani je nula).
Zatim na brojevnoj pravoj označavamo tačke u kojima brojnik ili imenilac ide na nulu.
Ove tačke dijele cijelu brojevnu pravu na intervale, na svakom od kojih razlomka-racionalna funkcija zadržava svoj predznak.
Ostaje samo da se otkrije njegov predznak u svakom intervalu.
To radimo provjeravanjem predznaka izraza u bilo kojoj tački koja pripada datom intervalu. Nakon toga zapisujemo odgovor. To je sve.
Ali postavlja se pitanje: da li se znakovi uvijek izmjenjuju? Ne ne uvek! Morate biti oprezni i ne postavljati znakove mehanički i nepromišljeno.
2. Razmotrimo još jednu nejednakost.
Class="tex" alt="\genfrac())()(0)(\displaystyle \left(x-2 \right)^2)(\displaystyle \left(x-1 \right) \ lijevo(x-3 \desno))>0"> !}
Ponovo postavite tačke na osu. Tačke i su probušene jer su nule nazivnika. Tačka je također izrezana, jer je nejednakost stroga.

Kada je brojnik pozitivan, oba faktora u nazivniku su negativna. Ovo se lako može provjeriti uzimanjem bilo kojeg broja iz datog intervala, na primjer, . Na lijevoj strani je znak:

Kada je brojnik pozitivan; Prvi faktor u nazivniku je pozitivan, drugi faktor je negativan. Na lijevoj strani je znak:

Situacija je ista! Brojač je pozitivan, prvi faktor u nazivniku je pozitivan, drugi je negativan. Na lijevoj strani je znak:

Konačno, sa class="tex" alt="x>3">
все множители положительны, и левая часть имеет знак :!} 
Odgovor: .
Zašto je poremećena izmjena znakova? Jer kada se prolazi kroz tačku, množitelj je „odgovoran“ za to nije promenio znak. Posljedično, cijela lijeva strana naše nejednakosti nije promijenila predznak.
zaključak: ako je linearni množitelj paran stepen (na primjer, na kvadrat), tada se prilikom prolaska kroz tačku znak izraza na lijevoj strani ne mijenja. U slučaju neparnog stepena, znak se, naravno, menja.
3. Hajde da razmotrimo više težak slučaj. Razlikuje se od prethodnog po tome što nejednakost nije stroga:
Lijeva strana je ista kao u prethodnom problemu. Slika znakova će biti ista:

Možda će odgovor biti isti? Ne! Rješenje se dodaje. To se događa jer su i lijeva i desna strana nejednakosti jednake nuli - dakle, ova tačka je rješenje.
Odgovor: .
Ova situacija se često javlja kod zadataka na Jedinstvenom državnom ispitu iz matematike. Ovdje kandidati upadaju u zamku i gube bodove. Budi pazljiv!
4. Šta učiniti ako se brojnik ili nazivnik ne mogu rastaviti na linearni faktori? Razmotrite ovu nejednakost:
Kvadratni trinom se ne može faktorizirati: diskriminanta je negativna, nema korijena. Ali ovo je dobro! To znači da je predznak izraza za sve isti, a posebno pozitivan. Više o tome možete pročitati u članku o svojstvima kvadratnih funkcija.
A sada možemo podijeliti obje strane naše nejednakosti vrijednošću koja je pozitivna za sve. Hajde da dođemo do ekvivalentne nejednakosti:
Što se lako rješava metodom intervala.
Imajte na umu da smo obje strane nejednakosti podijelili vrijednošću za koju smo sigurno znali da je pozitivna. Naravno, općenito, ne biste trebali množiti ili dijeliti nejednakost promjenljivom čiji je predznak nepoznat.
5 . Razmotrimo još jednu nejednakost, naizgled sasvim jednostavnu:
Samo želim da ga pomnožim sa . Ali mi smo već pametni i nećemo to učiniti. Uostalom, može biti i pozitivno i negativno. A znamo da ako se obje strane nejednakosti pomnože negativnom vrijednošću, predznak nejednakosti se mijenja.
Uradićemo to drugačije - skupićemo sve u jedan deo i dovesti do zajedničkog imenioca. Desna strana će ostati nula:
Class="tex" alt="\genfrac())()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}
I nakon toga - prijavite se intervalna metoda.
Na primjer, nejednakost je izraz \(x>5\).
Vrste nejednakosti:
Ako su \(a\) i \(b\) brojevi ili , tada se naziva nejednakost numerički. To je zapravo samo poređenje dva broja. Takve se nejednakosti dijele na vjerni I neveran.
Na primjer:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);
\(17+3\geq 115\) je netačna numerička nejednakost, jer je \(17+3=20\), a \(20\) manji od \(115\) (i nije veći ili jednak) .
Ako su \(a\) i \(b\) izrazi koji sadrže varijablu, onda imamo nejednakost sa varijablom. Takve se nejednakosti dijele na vrste ovisno o sadržaju:
|
\(2x+1\geq4(5-x)\) |
Varijabilno samo na prvi stepen |
|||
|
\(3x^2-x+5>0\) |
Postoji varijabla u drugom stepenu (kvadrat), ali nema viših stepena (treća, četvrta, itd.) |
|||
|
\(\log_(4)((x+1))<3\) |
||||
|
\(2^(x)\leq8^(5x-2)\) |
Šta je rješenje za nejednakost?
Ako nejednakost umjesto varijable zamijenite brojem, ona će se pretvoriti u brojčanu.
Ako data vrijednost za x pretvori izvornu nejednakost u pravu numeričku, onda se ona zove rješenje nejednakosti. Ako ne, onda ova vrijednost nije rješenje. I to riješiti nejednakost– potrebno je pronaći sva njegova rješenja (ili pokazati da ih nema).
Na primjer, ako zamenimo broj \(7\) u linearnu nejednačinu \(x+6>10\), dobićemo ispravnu numeričku nejednačinu: \(13>10\). A ako zamijenimo \(2\), doći će do netačne numeričke nejednakosti \(8>10\). To jest, \(7\) je rješenje izvorne nejednakosti, ali \(2\) nije.
Međutim, nejednakost \(x+6>10\) ima druga rješenja. Zaista, dobićemo ispravne numeričke nejednakosti zamjenom \(5\), i \(12\), i \(138\)... A kako možemo pronaći sva moguća rješenja? Za to koriste Za naš slučaj imamo:
\(x+6>10\) \(|-6\)
\(x>4\)
Odnosno, bilo koji broj veći od četiri je pogodan za nas. Sada morate zapisati odgovor. Rješenja nejednačina se obično pišu numerički, dodatno ih označavaju na brojevnoj osi senčenjem. Za naš slučaj imamo:
odgovor:
\(x\in(4;+\infty)\)
Kada se predznak nejednakosti mijenja?
Postoji jedna velika zamka u nejednakostima u koju učenici zaista „vole“ da upadnu:
Prilikom množenja (ili dijeljenja) nejednakosti negativnim brojem, ona se obrće („više“ za „manje“, „više ili jednako“ za „manje ili jednako“ i tako dalje)
Zašto se ovo dešava? Da bismo ovo razumjeli, pogledajmo transformacije numerička nejednakost\(3>1\). Tačno je, tri je zaista veće od jedan. Prvo, pokušajmo ga pomnožiti s bilo kojim pozitivnim brojem, na primjer, dva:
\(3>1\) \(|\cdot2\)
\(6>2\)
Kao što vidimo, nakon množenja nejednakost ostaje tačna. I bez obzira kojim pozitivnim brojem pomnožimo, uvijek ćemo dobiti tačnu nejednakost. Pokušajmo sada pomnožiti negativnim brojem, na primjer, minus tri:
\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)
Rezultat je netačna nejednakost, jer je minus devet manje od minus tri! Odnosno, da bi nejednakost postala istinita (i stoga je transformacija množenja negativnim bila "legalna"), trebate obrnuti znak poređenja, ovako: \(−9<− 3\).
Sa podjelom će ispasti na isti način, to možete sami provjeriti.
Gore napisano pravilo se odnosi na sve vrste nejednakosti, a ne samo na one numeričke.
primjer: Riješite nejednačinu \(2(x+1)-1<7+8x\)Rješenje:
|
\(2x+2-1<7+8x\) |
Pomaknimo \(8x\) ulijevo, a \(2\) i \(-1\) udesno, ne zaboravljajući da promijenimo znakove |
|
\(2x-8x<7-2+1\) |
|
|
\(-6x<6\) \(|:(-6)\) |
Podijelimo obje strane nejednakosti sa \(-6\), ne zaboravljajući da promijenimo iz "manje" u "više" |
|
Označimo numerički interval na osi. Nejednakost, stoga "izbodemo" samu vrijednost \(-1\) i ne uzimamo je kao odgovor |
|
|
Zapišimo odgovor kao interval |
odgovor: \(x\in(-1;\infty)\)
Nejednakosti i invaliditet
Nejednačine, baš kao i jednadžbe, mogu imati ograničenja na , odnosno na vrijednosti x. Shodno tome, one vrijednosti koje su prema DZ-u neprihvatljive treba isključiti iz raspona rješenja.
primjer: Riješite nejednačinu \(\sqrt(x+1)<3\)
Rješenje: Jasno je da da bi lijeva strana bila manja od \(3\), radikalni izraz mora biti manji od \(9\) (na kraju krajeva, od \(9\) samo \(3\)). Dobijamo:
\(x+1<9\) \(|-1\)
\(x<8\)
Sve? Bilo koja vrijednost x manja od \(8\) će nam odgovarati? Ne! Jer ako uzmemo, na primjer, vrijednost \(-5\) koja izgleda da odgovara zahtjevu, to neće biti rješenje izvorne nejednakosti, jer će nas dovesti do izračunavanja korijena negativnog broja.
\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)
Stoga moramo uzeti u obzir i ograničenja vrijednosti X - ona ne može biti takva da ispod korijena postoji negativan broj. Dakle, imamo drugi zahtjev za x:
\(x+1\geq0\)
\(x\geq-1\)
A da bi x bilo konačno rješenje, mora istovremeno zadovoljiti oba zahtjeva: mora biti manje od \(8\) (da bi bilo rješenje) i veće od \(-1\) (da bi u principu bilo prihvatljivo). Ucrtavajući to na brojevnu pravu, imamo konačni odgovor:

odgovor: \(\lijevo[-1;8\desno)\)
Pažnja!
Postoje dodatni
materijala u Posebnom dijelu 555.
Za one koji su veoma "ne baš..."
I za one koji "jako...")
Šta se desilo "kvadratna nejednakost"? Nema sumnje!) Ako uzmete bilo koji kvadratnu jednadžbu i zamijenite znak u njoj "=" (jednako) bilo kojem znaku nejednakosti ( > ≥ < ≤ ≠ ), dobijamo kvadratnu nejednakost. Na primjer:
1. x 2 -8x+12 ≥ 0
2. -x 2 +3x > 0
3. x 2 ≤ 4
Pa razumes...)
Nije uzalud ovdje povezao jednačine i nejednačine. Poenta je da je prvi korak u rješavanju bilo koji kvadratna nejednakost - riješiti jednačinu iz koje je ova nejednakost napravljena. Iz tog razloga, nemogućnost rješavanja kvadratnih jednačina automatski dovodi do potpunog neuspjeha u nejednačinama. Je li nagovještaj jasan?) Ako ništa drugo, pogledajte kako riješiti bilo koju kvadratnu jednačinu. Tamo je sve detaljno opisano. I u ovoj lekciji ćemo se pozabaviti nejednakostima.
Nejednačina spremna za rješenje ima oblik: na lijevoj strani je kvadratni trinom sjekira 2 +bx+c, desno - nula. Znak nejednakosti može biti apsolutno bilo šta. Prva dva primjera su ovdje već su spremni da donesu odluku. Treći primjer tek treba pripremiti.
Ako vam se sviđa ovaj sajt...
Inače, imam još par zanimljivih stranica za vas.)
Možete vježbati rješavanje primjera i saznati svoj nivo. Testiranje sa trenutnom verifikacijom. Učimo - sa interesovanjem!)
Možete se upoznati sa funkcijama i izvedenicama.