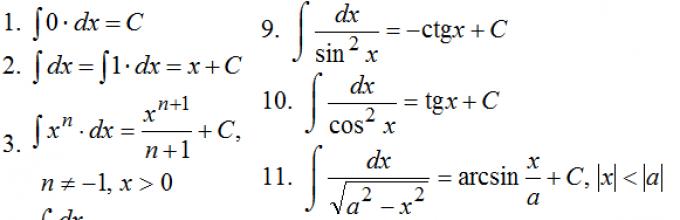Četiri glavne metode integracije su navedene u nastavku.
1)
Pravilo za integraciju zbira ili razlike.
.
Ovdje i ispod u, v, w su funkcije integracione varijable x.
2)
Premještanje konstante izvan predznaka integrala.
Neka je c konstanta nezavisna od x. Tada se može izvaditi iz predznaka integrala.
3)
Varijabilna metoda zamjene.
Razmotrimo neodređeni integral.
Ako možemo pronaći takvu funkciju φ (x) od x, dakle
,
tada, zamjenom varijable t = φ(x) , imamo
.
4)
Formula za integraciju po dijelovima.
,
gdje su u i v funkcije integracione varijable.
Konačni cilj proračuna neodređeni integrali- ovo je da se kroz transformacije zadati integral svede na najjednostavnije integrale, koji se nazivaju tabelarni integrali. Integrali tabele se izražavaju kroz elementarne funkcije koristeći poznate formule.
Vidi Tabelu integrala >>>
Primjer
Izračunaj neodređeni integral
Rješenje
Primećujemo da je integrand zbir i razlika tri člana:
, I .
Primjena metode 1
.
Zatim, primjećujemo da se integrandi novih integrala množe konstantama 5, 4,
I 2
, odnosno. Primjena metode 2
.
U tabeli integrala nalazimo formulu
.
Uz pretpostavku n = 2
, nalazimo prvi integral.
Prepišimo drugi integral u obliku
.
Primećujemo to. Onda
Koristimo treću metodu. Mijenjamo varijablu t = φ (x) = log x.
.
U tabeli integrala nalazimo formulu
Pošto se varijabla integracije može označiti bilo kojim slovom, onda
Prepišimo treći integral u obliku
.
Primjenjujemo formulu integracije po dijelovima.
Hajde da to stavimo.
Onda
;
;
;
;
.
Konačno imamo
.
Sakupimo pojmove sa x 3
.
.
Odgovori
Reference:
N.M. Gunther, R.O. Kuzmin, Zbirka zadataka iz više matematike, “Lan”, 2003.
Integracija je jedna od glavnih operacija u matematičkoj analizi. Tabele poznatih antiderivata mogu biti korisne, ali sada, nakon pojave sistema kompjuterske algebre, gube svoj značaj. Ispod je lista najčešćih primitiva.
Tabela osnovnih integrala
Druga, kompaktna opcija

Tablica integrala trigonometrijskih funkcija
Od racionalnih funkcija
Od iracionalnih funkcija
Integrali transcendentalnih funkcija

"C" je proizvoljna integraciona konstanta, koja se određuje ako je poznata vrijednost integrala u bilo kojoj tački. Svaka funkcija ima beskonačan broj antiderivata.
Većina školaraca i studenata ima problema s izračunavanjem integrala. Ova stranica sadrži integralne tabele od trigonometrijskih, racionalnih, iracionalnih i transcendentalnih funkcija koje će pomoći u rješavanju. Pomoći će vam i tabela izvedenica.
Video - kako pronaći integrale
Ako ne razumete sasvim ovu temu, pogledajte video, koji sve detaljno objašnjava.Tabela antiderivata
Koristeći svojstva neodređenih integrala i tablicu osnovnih integrala,
Možete integrirati neke funkcije.
TEHNIKE INTEGRACIJE
Metoda zamjene
Najčešća metoda integracije funkcija je metoda
zamjena, koja se primjenjuje kada se traži integral
je tabelarni, ali kroz niz elementarnih transformacija može biti
sveden na sto.
varijabla t se zamjenjuje promjenljivom / koristeći formulu x=φ(t) i,
dakle, dx je proizvod φ"(t)dt.
Integracija po dijelovima
Primjer: trebate pronaći integral
Ovdje dvostruke okomite linije obuhvataju sve proračune koje
pripremaju se za primenu formule integracije preko
dijelovi. Pripremni unosi se mogu uzeti izvan jednačine.
DEFINITIVNI INTEGRAL
Zadatak. Naći prirast funkcije koji je antiderivat funkcije f(x), kada
tranzicija argumenta x sa vrijednosti a na vrijednost b.
Rješenje. Pretpostavimo da smo integracijom pronašli
Kao što vidimo, u izrazu za prirast antiderivativna funkcija F(x) + C 1
ne postoji konstantna vrijednost C1. I pošto je C 1 značio bilo koji
dati broj, onda dobijeni rezultat dovodi do sljedećeg zaključka: kada
prijelaz argumenta x sa vrijednosti x=a na vrijednost x=b, sve funkcije F(x) + C,
antiderivati za datu funkciju f(x) imaju isti prirast jednak
F(b)-F(a).
Ovaj prirast se obično naziva definitivnim integralom i označava
simbol
Dakle, traženi integral je jednak 6.
Geometrijsko značenje definitivni integral
1. Nađite površinu jednog luka sinusoida.
Tijelo okretanja je prikazano na slici.
Za avion ću izabrati xy ravan.
Primjer br. 2. Pronalaženje određenog integrala pomoću metode promjene varijabli
integracija
Primjer br. 3. Pronalaženje određenog integrala integracijom preko
dijelovi.
Odnosi između mase m i gustine p:
Odnosi između električni naboj q i jačina struje I:
Odnos između toplotnog kapaciteta c i količine toplote Q:
Opis kretanja viskozne tečnosti, krvi kroz sudove, distribucije
krvni pritisak u kardiovaskularnom sistemu, termički, električni,
magnetski, optički procesi povezani sa životom
organizam, zahtijeva korištenje integracije.
OBUKA: RJEŠAVANJE PRIMJERA
tačke se mijenjaju po zakonu v = (6t +7) m/s
Odredite kako pređeni put ovisi o vremenu ako je brzina materijala
tačke se menjaju po zakonu v = (6t +7) m/s, ako je poznato da u početnom trenutku
vrijeme (t=0), materijalna tačka nalazio se na udaljenosti s 0 = 4 m od početka
Nađite rad opruge kada je proširena sa x 1 na x 2.
Rješenje.
Da biste integrirali ovu funkciju, morate izvršiti zamjenu
varijabla
Pošto na segmentu [-1;2] ima 4 2 ≤2, tada se izračunava površina S ove figure
na sljedeći način:
Rješenje.
u=sinx
du = cosxdx
nove granice integracije: u 1 = 0 (pošto je x 1 = 0, zamijenimo ovu vrijednost novom
funkcija - u = sinx, u 1 = sinx 1 = 0)
pojava indukcijske struje u njemu,
| |
| odgovor: |
DIFERENCIJALNE JEDNAČINE
Diferencijalne jednadžbe su jednadžbe koje sadrže traženo
funkcije, njihove derivate različitih redova i nezavisne varijable.
Teorija diferencijalnih jednačina nastala je krajem 17. vijeka pod
uticaj potreba mehanike i drugih prirodnih nauka,
u suštini istovremeno sa integralnim računom i
diferencijalni račun.
Najjednostavnije diferencijalne jednadžbe su se već susrele u radovima I.
Newton i G. Leibniz; izraz "diferencijalne jednadžbe"
pripada Leibnizu. Problem nalaženja neodređenog integrala F (x)
funkcije f(x) Njutn smatra jednostavno kao poseban slučaj njegov drugi
zadataka. To je bio pristup za Newtona, kao tvorca temelja
matematička prirodna nauka potpuno je opravdana: u veoma velikom
U mnogim slučajevima, zakoni prirode koji upravljaju određenim procesima,
izražavaju se u obliku diferencijalnih jednačina, a proračun protoka istih
procesi se svode na rješavanje diferencijalnih jednadžbi.
Sljedeća dva jednostavni primjeri može poslužiti kao ilustracija
šta je rečeno.
1) Ako se tijelo zagrijano na temperaturu T stavi u medij, temperatura
što je jednako nuli, onda pod određenim uslovima možemo pretpostaviti da
povećanje ΔT (negativno u slučaju T> 0) njegove temperature preko malog
vremenski interval Δt se izražava sa dovoljnom tačnošću formulom
gdje je k konstantan koeficijent. Prilikom matematičke obrade
fizički problem vjerujem da je upravo to odgovarajuće
granični omjer između diferencijala
tj. odvija se diferencijalna jednadžba
gdje T označava derivaciju br.
rastezanje opruge dovodi do opterećenja
pokret. Ako x(t) označava
količina odstupanja tijela od
ravnotežni položaj u ovom trenutku
vrijeme t, zatim ubrzanje tijela
izražava se 2. izvodom x" (t).
Sila tx" (t) koja djeluje na tijelo je
sa malim delovima opruge
prema zakonima teorije elastičnosti, proporcionalna je devijaciji x (t). to.,
dobijamo diferencijalnu jednacinu
 |
| Njegovo rešenje izgleda ovako: |