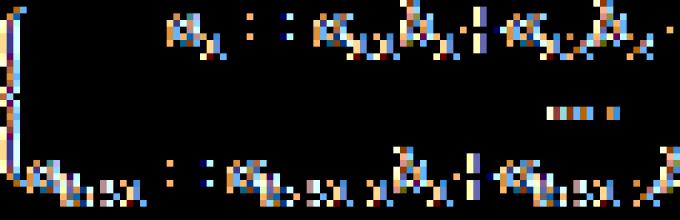Lema 1 : Ako je u matrici veličine n n barem jedan red (kolona) jednak nuli, tada su redovi (kolone) matrice linearno zavisni.

dokaz: Neka je tada prvi red nula

Gdje a 1 0. To je ono što se tražilo.

definicija: Poziva se matrica čiji su elementi koji se nalaze ispod glavne dijagonale jednaki nuli trouglasti:

i ij = 0, i>j.

Lema 2: Determinanta trokutaste matrice jednaka je proizvodu elemenata glavne dijagonale.

Dokaz je lako izvesti indukcijom na dimenziju matrice.

Teorema O linearnu nezavisnost vektori.

A)Nužnost: linearno zavisna D=0 .

dokaz: Neka budu linearno zavisni, j=,

to jest, postoji j , nisu svi jednaki nuli, j= ,Šta a 1 A 1 + a 2 A 2 + ... a n A n = , A j – matrične kolone A. Neka, na primjer, a n¹0.

Imamo a j * = a j / a n , j£ n-1a 1 * A 1 + a 2 * A 2 + ... a n -1 * A n -1 + A n = .

Zamijenimo zadnji stupac matrice A on

A n * = a 1 * A 1 + a 2 * A 2 + ... a n -1 A n -1 + A n = .

Prema gore dokazanom svojstvu determinante (neće se promijeniti ako se u bilo koji stupac u matrici doda još jedan stupac pomnožen brojem), determinanta nove matrice jednaka je determinanti originalne. Ali u novoj matrici jedan stupac je nula, što znači da, širenjem determinante preko ovog stupca, dobijamo D=0, Q.E.D.

b)Adekvatnost: Matrica veličine n nsa linearno nezavisnim redovima uvijek se može svesti na trouglasti oblik korištenjem transformacija koje se ne mijenjaju apsolutna vrijednost odrednica. Štaviše, iz nezavisnosti redova originalne matrice sledi da je njena determinanta jednaka nuli.

1. Ako je u matrici veličine n n sa linearno nezavisnim elementom redova a 11 je jednak nuli, zatim stupac čiji element a 1 j ¹ 0. Prema lemi 1, takav element postoji. Determinanta transformisane matrice može se razlikovati od determinante originalne matrice samo u znaku.

2. Iz redova sa brojevima i>1 oduzmi prvi red pomnozen razlomkom a i 1 /a 11. Štaviše, u prvoj koloni redova sa brojevima i>1 rezultiraće nula elemenata.

3. Počnimo računati determinantu rezultirajuće matrice dekomponiranjem preko prve kolone. Pošto su svi elementi u njemu osim prvog jednaki nuli,

D novo = a 11 novih (-1) 1+1 D 11 novih,

Gdje d 11 novo je determinanta matrice manje veličine.

Dalje, za izračunavanje determinante D 11 ponavljajte korake 1, 2, 3 dok se posljednja determinanta ne pokaže kao determinanta matrice veličine 1 1. Pošto korak 1 samo mijenja predznak determinante matrice koja se transformira, a korak 2 uopće ne mijenja vrijednost determinante, onda ćemo do predznaka na kraju dobiti determinantu originalne matrice. U ovom slučaju, budući da je zbog linearne nezavisnosti redova originalne matrice, korak 1 uvijek zadovoljen, svi elementi glavne dijagonale će se pokazati nejednakim nuli. Dakle, konačna determinanta, prema opisanom algoritmu, jednaka je proizvodu različitih elemenata na glavnoj dijagonali. Dakle, determinanta originalne matrice nije jednaka nuli. Q.E.D.

Dodatak 2

U nastavku je dato nekoliko kriterijuma za linearnu zavisnost i, shodno tome, linearnu nezavisnost vektorskih sistema.

Teorema. (Neophodan i dovoljan uslov za linearnu zavisnost vektora.)

Sistem vektora je zavisan ako i samo ako je jedan od vektora sistema linearno izražen kroz ostale u ovom sistemu.

Dokaz. Nužnost. Neka je sistem linearno zavisan. Tada, po definiciji, predstavlja nulti vektor netrivijalno, tj. postoji netrivijalna kombinacija ovog sistema vektora jednaka nultom vektoru:

pri čemu barem jedan od koeficijenata ove linearne kombinacije nije jednak nuli. Neka , .

Podijelimo obje strane prethodne jednakosti ovim koeficijentom koji nije nula (tj. pomnožimo sa:

Označimo: , gdje .

one. jedan od vektora sistema se linearno izražava kroz ostale ovog sistema itd.

Adekvatnost. Neka je jedan od vektora sistema linearno izražen kroz druge vektore ovog sistema:

Pomaknimo vektor desno od ove jednakosti:

Pošto je koeficijent vektora jednak , onda imamo netrivijalnu reprezentaciju nule sistemom vektora, što znači da je ovaj sistem vektora linearno zavisan, itd.

Teorema je dokazana.

Posljedica.

1. Vektorski sistem vektorski prostor je linearno nezavisna ako i samo ako nijedan od vektora sistema nije linearno izražen u terminima drugih vektora ovog sistema.

2. Sistem vektora koji sadrži nulti vektor ili dva jednaka vektora je linearno zavisan.

Dokaz.

1) Nužnost. Neka je sistem linearno nezavisan. Pretpostavimo suprotno i postoji vektor sistema koji je linearno izražen kroz druge vektore ovog sistema. Tada je, prema teoremi, sistem linearno zavisan i dolazimo do kontradikcije.

Adekvatnost. Neka nijedan od vektora sistema ne bude izražen u terminima ostalih. Pretpostavimo suprotno. Neka je sistem linearno zavisan, ali onda iz teoreme proizilazi da postoji vektor sistema koji je linearno izražen kroz druge vektore ovog sistema i opet dolazimo do kontradikcije.

2a) Neka sistem sadrži nulti vektor. Pretpostavimo radi određenosti da je vektor :. Tada je jednakost očigledna

one. jedan od vektora sistema je linearno izražen kroz ostale vektore ovog sistema. Iz teoreme slijedi da je takav sistem vektora linearno zavisan, itd.

Imajte na umu da se ova činjenica može dokazati direktno iz linearno zavisnog sistema vektora.

Budući da , sljedeća jednakost je očigledna

Ovo je netrivijalan prikaz nultog vektora, što znači da je sistem linearno zavisan.

2b) Neka sistem ima dva jednaka vektora. Neka za . Tada je jednakost očigledna

One. prvi vektor je linearno izražen kroz preostale vektore istog sistema. Iz teoreme slijedi da ovaj sistem linearno zavisna, itd.

Slično kao i prethodni, ova tvrdnja se može dokazati direktno definicijom linearno zavisnog sistema.Tada ovaj sistem netrivijalno predstavlja nulti vektor

odakle sledi linearna zavisnost sistema.

Teorema je dokazana.

Posljedica. Sistem koji se sastoji od jednog vektora je linearno nezavisan ako i samo ako je ovaj vektor različit od nule.

Def. Skup w naziva se linearni prostor, a njegov element. -vektori ako:

*zakon je određen (+) prema kat. bilo koja dva elementa x, y iz w pridružena su elementu pod nazivom. njihov zbir [x + y]

*dat je zakon (* za broj a), prema cat elementu x iz w i a, upoređuje se element iz w, koji se naziva proizvod x i a [ax];

* završeno

sljedeće zahtjeve (ili aksiome):

Trag c1. nulti vektor (ctv 0 1 i 0 2. prema a3: 0 2 + 0 1 = 0 2 i 0 1 + 0 2 = 0 1. prema a1 0 1 + 0 2 = 0 2 + 0 1 => 0 1 = 0 2.)

c2. .(ctv, a4)

c3. 0 vec.(a7)

c4. a(broj)*0=0.(a6,c3)

c5. x (*) -1 =0 vektor, suprotno od x, tj. (-1)x = -x. (a5,a6)

c6. U w je definirana akcija oduzimanja: vektor x naziva se razlika vektora b i a, ako je x + a = b, i označava se x = b - a.

Broj n pozvao dimenzija lin. pr-a L , ako je u L postoji sistem n lin. nezav. vektori i bilo koji sistem od n+1 vektor - lin. zavisan dim L= n. Prostor L nazivaju n-dimenzionalnim.

Uređena zbirka od n linija. nezav. vektori n dimenzionalno nezavisni. prostor - osnovu

Teorema. Svaki vektor X može se predstaviti na jedinstven način kao linija Kombinacije baznih vektora

Neka je (1) osnova n-dimenzionalnog lineara. pr-va V, tj. zbirka linearno nezavisnih vektora. Skup vektora će biti linearan. zavisna, jer njihov n+ 1.

One. postoje brojevi koji nisu svi jednaki nuli u isto vrijeme, kakve to veze ima s tim (inače (1) su linearno zavisne).

Onda gdje je vektorska dekompozicija x po osnovu(1) .

Ovaj izraz je jedinstven, jer ako postoji drugi izraz (**)

oduzimanje jednakosti (**) od (*),

dobijamo

Jer su linearno nezavisni, onda . Chtd

Teorema. Ako - lin. nezavisni vektori prostora V i svaki vektor x iz V mogu se predstaviti kroz , tada ovi vektori čine osnovu V

Doc: (1)-lin.independent =>dokument ostaje linearno nezavisan. Prema konvenciji Svaki vektor a je izražen kroz (1): , uzmite u obzir , rang≤n => među stupcima ne više od n su linearno neovisni, ali m > n=> m stupaca su linearno zavisni => s=1, n

To jest, vektori su linearno zavisni

Dakle, prostor V je n-dimenzionalan i (1) njegova baza

№4Def. Podskup L lin. proizvodnja V naziva se lin. kond. ovog prostora ako je, s obzirom na operacije (+) i (*a) specificirane u V, podprostor L linearni prostor

Teorema Skup l vektora prostora V je linearan. Podprostor ovog prostora izvodi

(unapred) neka su (1) i (2) zadovoljene, da bi L bilo subjednostavno. V ostaje dokazati da su svi aksiomi lin zadovoljeni. pr-va.

(-x): -x+x=0 d. a(x + y) = ax + ay;

(a-b) i (e-h) proizlazi iz valjanosti V; dokažimo (c)

(neophodnost) Neka je L lin. podprostora ovog prostora, tada su (1) i (2) zadovoljene na osnovu definicije linija. pr-va

Def. Kolekcija svih vrsta linija. kombinacije nekih elemenata (x j) lin. proizvod se naziva linearna ljuska

Teorema proizvoljan skup svih linija. kombinacije vektora V sa realnim. koeficijent je lin. podpr V (linearna ljuska dati sistem vektora lin. pr. je linearni potpr. ovog pr. )

ODA.Neprazan podskup L linijskih vektora. proizvodnja V naziva se lin. podprostor ako:

a) zbir svih vektora iz L pripada L

b) proizvod svakog vektora iz L za bilo koji broj pripada L

Zbir dva podprostoraLje opet podprostorL

1) Neka je y 1 +y 2 (L 1 +L 2)<=>y 1 =x 1 +x 2, y 2 =x’ 1 +x’ 2, gdje je (x 1,x’ 1) L 1, (x 2,x’ 2) L 2. y 1 +y 2 =(x 1 +x 2)+(x' 1 +x' 2)=(x 1 +x' 1)+(x 2 +x' 2), gdje je (x 1 +x' 1 ) L 1 , (x 2 +x' 2) L 2 => prvi uslov linearnog podprostora je zadovoljen.

ay 1 =ax 1 +ax 2, gdje je (ax 1) L 1, (ax 2) L 2 => jer (y 1 +y 2) (L 1 +L 2) , (ly 1) (L 1 +L 2) => uslovi su ispunjeni => L 1 +L 2 je linearni podprostor.

Raskrsnica dviju parcelaL 1 IL 2 lin. pr-vaL je također subsp. ovaj prostor.

Razmotrimo dva proizvoljna vektora x,y, koji pripada presjeku podprostora, i dva proizvoljna broja a,b:.

Prema def. presjeci skupova:

=> po definiciji podprostora linearnog prostora:,.

T.K. vektor sjekira + by pripada mnogima L 1, i mnogi L 2, onda pripada, po definiciji, presjeku ovih skupova. ovako:

ODA.Kažu da je V direktan zbir njegovih potpodjela. ako i b) ova dekompozicija je jedinstvena

b") Pokažimo da je b) ekvivalentno b’)

Kada je b) tačno b')

Sve vrste (M, N) od seku samo duž nultog vektora

Neka je ∃ z ∈

Fer povratakL=

kontradikcija

Teorema To (*) je neophodno i dovoljno za uniju baza ( činio osnovu prostora

(obavezno) neka (*) i vektori budu baze podskupova. i postoji ekspanzija u ; x se proširuje preko baze L, da bi se konstatovalo da ( čine bazu, potrebno je dokazati njihovu linearnu nezavisnost; svi sadrže 0 0=0+...+0. Zbog jedinstvenosti proširenja 0 preko : => zbog linearne nezavisnosti baze => ( – baza

(Ext.) Neka ( čini osnovu L jedinstvene dekompozicije (**) postoji barem jedna dekompozicija. Po jedinstvenosti (*) => jedinstvenosti (**)

Komentar. Dimenzija direktnog zbira jednaka je zbiru dimenzija podprostora

Bilo koja nesingularna kvadratna matrica može poslužiti kao prijelazna matrica s jedne baze na drugu

Neka je n dimenzionalno linearni prostor V postoje dvije baze i

(1) =A, gdje elementi * i ** nisu brojevi, ali ćemo određene operacije na numeričkoj matrici proširiti na takve redove.

Jer inače bi vektori ** bili linearno zavisni

Nazad. Ako su tada stupci A linearno nezavisni =>formiraju osnovu

Koordinate I povezane relacijom , Gdje elementi prelazne matrice

Neka bude poznata dekompozicija elemenata “nove” osnove u “staru”.

Tada su jednakosti tačne

Ali ako je linearna kombinacija linearno nezavisnih elemenata 0 onda je =>

Osnovna teorema linearne zavisnosti

Ako (*) se linearno izražava kroz (**) Ton<= m

Dokažimo indukcijom na m

m=1: sistem (*) sadrži 0 i lin. menadžer - nemoguće

neka je tačno za m=k-1

dokažimo za m=k

Može se ispostaviti da 1) , tj. v-ry (1) su lin.comb. lin. u jarku (2)Sistem (1) linearni nepouzdan, jer je dio lin.nezav. sistemi (*). Jer u sistemu (2) postoji samo k-1 vektora, tada hipotezom indukcije dobijamo k+1 3.3. Linearna nezavisnost vektora. Osnova.

Linearno kombinacija vektorski sistemi

zove se vektor

gdje je a 1, a 2, ..., a n - proizvoljni brojevi.

Ako sve a i = 0, tada se poziva linearna kombinacija trivijalan . U ovom slučaju, očigledno

Definicija 5.

Ako je za sistem vektora postoji netrivijalna linearna kombinacija (barem jedna ai¹ 0) jednako nultom vektoru: tada se sistem vektora naziva linearno zavisan. Ako je jednakost (1) moguća samo u slučaju kada su sve a i =0, tada se sistem vektora zove linearno nezavisni .

Teorema 2 (Uvjeti linearne zavisnosti).

Definicija 6.

Iz teoreme 3 slijedi da ako je baza data u prostoru, onda dodavanjem proizvoljnog vektora na nju dobijamo linearno zavisan sistem vektora. U skladu sa Teorema 2 (1) , jedan od njih (može se pokazati da se vektor) može predstaviti kao linearna kombinacija ostalih:

.

Definicija 7.

Brojevi su pozvani koordinate vektori u bazi (označeno

Ako se vektori razmatraju na ravni, tada će osnova biti uređeni par nekolinearnih vektora

a koordinate vektora u ovoj osnovi su par brojeva:

Napomena 3. To se može pokazati za datu osnovu, koordinate vektora se određuju jedinstveno . Iz ovoga, posebno, proizilazi da ako su vektori jednaki, tada su im odgovarajuće koordinate jednake, i obrnuto .

Dakle, ako je baza data u prostoru, onda svaki vektor prostora odgovara uređenoj trojci brojeva (koordinate vektora u ovoj bazi) i obrnuto: svaka trojka brojeva odgovara vektoru.

Na ravni se uspostavlja slična korespondencija između vektora i parova brojeva.

Teorema 4 (Linearne operacije kroz vektorske koordinate).

Ako u nekoj osnovi I a je proizvoljan broj, onda u ovoj osnovi

Drugim riječima:

Kada se vektor pomnoži sa brojem, njegove koordinate se množe s tim brojem ;

pri dodavanju vektora dodaju se njihove odgovarajuće koordinate .

Primjer 1 . U nekim osnovama vektoriimaju koordinate

Pokažite da vektori čine osnovu i pronađite koordinate vektora u toj bazi.

Vektori čine osnovu ako nisu komplanarni, dakle (u skladu sa prema teoremi 3(2) ) su linearno nezavisne.

Po definiciji 5 to znači da je jednakost

moguće samo akox = y = z = 0.

Funkcije se pozivaju linearno nezavisna, Ako

(dozvoljena je samo trivijalna linearna kombinacija funkcija koja je identično jednaka nuli). Za razliku od linearne nezavisnosti vektora, ovdje je linearna kombinacija identična nuli, a ne jednakosti. Ovo je razumljivo, jer jednakost linearne kombinacije sa nulom mora biti zadovoljena za bilo koju vrijednost argumenta.

Funkcije se pozivaju linearno zavisna, ako postoji skup konstanti različit od nule (nisu sve konstante jednake nuli) tako da (postoji netrivijalna linearna kombinacija funkcija identično jednaka nuli).

Teorema.Da bi funkcije bile linearno zavisne, potrebno je i dovoljno da bilo koja od njih bude linearno izražena kroz druge (predstavljena kao njihova linearna kombinacija).

Dokažite ovu teoremu sami; ona se dokazuje na isti način kao i slična teorema o linearnoj zavisnosti vektora.

Odrednica Vronskog.

Determinanta Wronskog za funkcije je uvedena kao determinanta čiji su stupci derivati ​​ovih funkcija od nule (samih funkcija) do n-1. reda.

.

Teorema. Ako funkcije su, dakle, linearno zavisne

Dokaz. Pošto funkcije su linearno zavisne, onda se bilo koji od njih linearno izražava kroz ostale, npr.

Identitet se može razlikovati, dakle

Tada se prvi stupac determinante Wronskog linearno izražava kroz preostale kolone, pa je determinanta Wronskog identično jednaka nuli.

Teorema.Da bi rješenja linearne homogene diferencijalne jednadžbe n-tog reda bila linearno zavisna, potrebno je i dovoljno da.

Dokaz. Neophodnost sledi iz prethodne teoreme.

Adekvatnost. Hajde da popravimo neku tačku. Budući da su stupci determinante izračunati u ovoj tački linearno zavisni vektori.

, da su odnosi zadovoljni

Kako je linearna kombinacija rješenja linearne homogene jednadžbe njeno rješenje, možemo uvesti rješenje oblika

Linearna kombinacija rješenja sa istim koeficijentima.

Imajte na umu da ovo rješenje zadovoljava nulte početne uslove, što proizilazi iz gore napisanog sistema jednačina. Ali trivijalno rješenje linearne homogene jednačine također zadovoljava iste nulte početne uslove. Dakle, iz Cauchyjeve teoreme slijedi da je uvedeno rješenje identično jednako trivijalnom, dakle,

stoga su rješenja linearno zavisna.

Posljedica.Ako determinanta Wronskog, izgrađena na rješenjima linearne homogene jednadžbe, nestane barem u jednoj tački, onda je identično jednaka nuli.

Dokaz. Ako , tada su rješenja linearno zavisna, dakle, .

Teorema.1. Za linearnu zavisnost rješenja potrebno je i dovoljno(ili ).

2. Za linearnu nezavisnost rješenja potrebno je i dovoljno.

Dokaz. Prva tvrdnja proizilazi iz teoreme i prethodno dokazane posljedice. Druga tvrdnja se može lako dokazati kontradikcijom.

Neka su rješenja linearno nezavisna. Ako je , tada su rješenja linearno zavisna. Kontradikcija. dakle, .

Neka . Ako su rješenja linearno zavisna, onda , dakle, kontradikcija. Dakle, rješenja su linearno nezavisna.

Posljedica.Nestanak determinante Wronskog barem u jednoj tački je kriterij za linearnu ovisnost rješenja linearne homogene jednadžbe.

Razlika između determinante Wronskog i nule je kriterij za linearnu neovisnost rješenja linearne homogene jednadžbe.

Teorema.Dimenzija prostora rješenja linearne homogene jednadžbe n-tog reda jednaka je n.

Dokaz.

a) Pokažimo da postoji n linearno nezavisnih rješenja linearne homogene diferencijalne jednadžbe n-tog reda. Hajde da razmotrimo rešenja , zadovoljava sljedeće početne uslove:

...........................................................

Takva rješenja postoje. Zaista, prema Cauchyjevoj teoremi, kroz tačku prolazi kroz jednu integralnu krivu – rješenje. Kroz tačku rješenje prolazi kroz tačku

- rješenje, kroz tačku - rešenje.

Ova rješenja su linearno nezavisna, jer .

b) Pokažimo da je svako rješenje linearne homogene jednadžbe linearno izraženo kroz ova rješenja (njihova je linearna kombinacija).

Razmotrimo dva rješenja. Jedan - proizvoljno rješenje sa početnim uslovima . Fer omjer