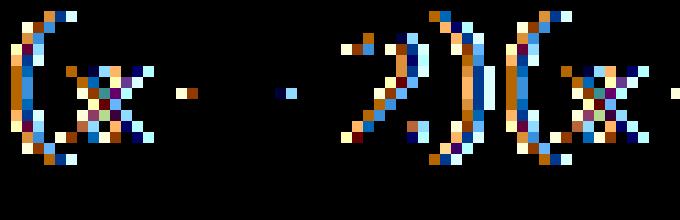To je kvadrat i sastoji se od tri člana (). Tako se ispostavilo - kvadratni trinom.
Primjeri Ne kvadratni trinomi:
\(x^3-3x^2-5x+6\) - kubni kvadrinom
\(2x+1\) - linearni binom
Kvadratni korijen trinoma:
primjer:
Trinom \(x^2-2x+1\) ima korijen \(1\), jer \(1^2-2 1+1=0\)
Trinom \(x^2+2x-3\) ima korijen \(1\) i \(-3\), jer \(1^2+2-3=0\) i \((-3)^ 2-6-3=9-9=0\)
Na primjer: ako trebate pronaći korijene za kvadratni trinom \(x^2-2x+1\), izjednačavamo ga sa nulom i rješavamo jednačinu \(x^2-2x+1=0\).
\(D=4-4\cdot1=0\)
\(x=\frac(2-0)(2)=\frac(2)(2)=1\)
Spreman. Korijen je \(1\).
Dekompozicija kvadratnog trinoma na:
Kvadratni trinom \(ax^2+bx+c\) može se proširiti kao \(a(x-x_1)(x-x_2)\) ako su jednačine \(ax^2+bx+c=0\) veće od nule \ (x_1\) i \(x_2\) su korijeni iste jednadžbe).
Na primjer, razmotrimo trinom \(3x^2+13x-10\).
U kvadratna jednačina\(3x^2+13x-10=0\) diskriminanta je 289 (veća od nule), a korijeni su \(-5\) i \(\frac(2)(3)\). Prema tome \(3x^2+13x-10=3(x+5)(x-\frac(2)(3))\). Lako je provjeriti ispravnost ove izjave - ako smo , onda ćemo dobiti originalni trinom.
Kvadratni trinom \(ax^2+bx+c\) se može predstaviti kao \(a(x-x_1)^2\) ako je diskriminanta jednačine \(ax^2+bx+c=0\) nula.
Na primjer, razmotrimo trinom \(x^2+6x+9\).Kvadratna jednačina \(x^2+6x+9=0\) ima diskriminant jednak \(0\) i jedinstveni korijen jednak \(-3\). To znači \(x^2+6x+9=(x+3)^2\) (ovdje je koeficijent \(a=1\), tako da se ne piše ispred zagrade - nema potrebe). Imajte na umu da istu konverziju može izvršiti .
Kvadratni trinom \(ax^2+bx+c\) se ne može faktorizirati ako je diskriminanta jednačine \(ax^2+bx+c=0\) manja od nule.
Na primjer, trinomi \(x^2+x+4\) i \(-5x^2+2x-1\) imaju diskriminant manji od nule. Stoga ih je nemoguće razdvojiti.
Primjer
. Faktor \(2x^2-11x+12\).
Rješenje
:
Nađimo korijene kvadratne jednadžbe \(2x^2-11x+12=0\)
\(D=11^2-4 \cdot 2 \cdot 12=121-96=25>0\)
\(x_1=\frac(11-5)(4)=1,5;\) \(x_2=\frac(11+5)(4)=4.\)
Dakle, \(2x^2-11x+12=2(x-1.5)(x-4)\)
Odgovori
: \(2(x-1,5)(x-4)\)
Rezultirajući odgovor može se napisati drugačije: \((2x-3)(x-4)\).
Primjer
. (Zadatak od OGE) Kvadratni trinom faktorizirano \(5x^2+33x+40=5(x++ 5)(x-a)\). Pronaci\).
Rješenje:
\(5x^2+33x+40=0\)
\(D=33^2-4 \cdot 5 \cdot 40=1089-800=289=17^2\)
\(x_1=\frac(-33-17)(10)=-5\)
\(x_2=\frac(-33+17)(10)=-1.6\)
\(5x^2+33x+40=5(x+5)(x+1.6)\)
Odgovori
: \(-1,6\)
Kvadratni trinom se može razložiti na sljedeći način:
A x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2)
gdje je a broj, koeficijent prije vodećeg koeficijenta,
x – promenljiva (tj. slovo),
x 1 i x 2 su brojevi, korijeni kvadratne jednadžbe a x 2 + b x + c = 0, koji se nalaze preko diskriminanta.
Ako kvadratna jednadžba ima samo jedan korijen, onda proširenje izgleda ovako:
a x 2 + b x + c = a ⋅ (x − x 0) 2
Primjeri faktoringa kvadratnog trinoma:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = (− 1) ⋅ (x − (− 1)) (x − 7) = − (x + 1) (x − 7) = (x + 1) (7 − x)
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = (− 1) ⋅ (x − 2) 2 = − (x − 2) 2
Ako je kvadratni trinom nepotpun (b = 0 ili c = 0), onda se može razložiti na sljedeće načine:
- c = 0 ⇒ a x 2 + b x = x (a x + b)
- b = 0 ⇒ primijeniti skraćenu formulu množenja za razliku kvadrata.
Zadaci za samostalno rješavanje
br. 1. Kvadratni trinom je faktorisan: x 2 + 6 x − 27 = (x + 9) (x − a) . Pronaci.
Rješenje:
Prvo trebate izjednačiti kvadratni trinom sa nulom da biste pronašli x 1 i x 2.
x 2 + 6 x − 27 = 0
a = 1, b = 6, c = − 27
D = b 2 − 4 a c = 6 2 − 4 ⋅ 1 ⋅ (− 27) = 36 + 108 = 144
D > 0 znači da će postojati dva različita korijena.
x 1,2 = − b ± D 2 a = − 6 ± 144 2 ⋅ 1 = [ − 6 + 12 2 = 6 2 = 3 − 6 − 12 2 = − 18 2 = − 9
Poznavajući korijene, faktoriziramo kvadratni trinom:
x 2 + 6 x − 27 = (x − (− 9)) (x − 3) = (x + 9) (x − 3)
br. 2. Jednačina x 2 + p x + q = 0 ima korijene − 5; 7. Pronađite q.
Rješenje:
1 način:(treba znati kako razložiti kvadratni trinom na faktore)
Ako su x 1 i x 2 korijeni kvadratnog trinoma a x 2 + b x + c, onda se može faktorizirati na sljedeći način: a x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2) .
Budući da je u datom kvadratnom trinomu vodeći koeficijent (faktor ispred x 2) jednak jedan, proširenje će biti kako slijedi:
x 2 + p x + q = (x − x 1) (x − x 2) = (x − (− 5)) (x − 7) = (x + 5) (x − 7) = x 2 − 7 x + 5 x − 35 = x 2 − 2 x − 35
x 2 + p x + q = x 2 − 2 x − 35 ⇒ p = − 2, q = − 35
Metoda 2: (treba znati Vietinu teoremu)
Vietina teorema:
Zbir korijena reduciranog kvadratnog trinoma x 2 + p x + q jednak je njegovom drugom koeficijentu p suprotnog predznaka, a proizvod je besplatni član q.
( x 1 + x 2 = − p x 1 ⋅ x 2 = q
q = x 1 ⋅ x 2 = (− 5) ⋅ 7 = − 35.
Prije svega, da ukažemo na neka uobičajena imena. Razmotrimo polinome koji sadrže samo jedno slovo, na primjer, slovo x. Tada je najjednostavniji polinom u kojem postoje dva člana, a jedan od njih sadrži slovo x do prvog stepena, a drugi uopće nema slovo x, na primjer 3x – 5 ili 15 – 7x ili 8z + 7 (ovdje umjesto slova x uzima se slovo z), itd. Takvi polinomi se nazivaju linearni binomi .
3x² – 5x + 7 ili x² + 2x – 1
ili 5y² + 7y + 8 ili z² – 5z – 2, itd.
Takvi polinomi se nazivaju kvadratni trinomi.
Tada možemo formirati kubni kvadrinom, na primjer:
x³ + 2x² – x + 1 ili 3x³ – 5x² – 2x – 3 itd.,
polinom četvrtog stepena, na primjer:
x 4 – 2x³ – 3x² + 4x – 5, itd.
Moguće je označiti koeficijente na x, na x², na x³ itd. i slovima, na primjer, slovima a, b, c, itd. Tada dobijamo:
1) opšti oblik binoma ax + b, linearan u odnosu na x,
2) opšti oblik kvadratnog trinoma (u odnosu na x): ax² + bx + c,
3) opšti oblik kubnog trinoma (u odnosu na x): ax³ + bx² + cx + d, itd.
Zamjenom slova a, b, c, d... u ovim formulama različitim brojevima, dobijamo sve vrste linearnih binoma, kvadratnih trinoma, itd. Na primjer, u formuli ax² + bx + c, koja izražava opće u obliku kvadratnog trinoma, slovo a zamijenimo brojem + 3, slovo b brojem –2 i slovo brojem –1, dobijemo kvadratni trinom 3x² – 2x – 1. U konkretnom slučaju, također je moguće dobiti binom zamjenom jednog od slova nulom, na primjer, ako je a = +1, b = 0 i c = –3, onda ćemo dobiti kvadratni binom x² – 3.
Možete naučiti da delite neke kvadratne trinome prilično brzo u linearne faktore. Mi ćemo se, međutim, ograničiti na razmatranje samo onih kvadratnih trinoma koji zadovoljavaju sljedeće uvjete:
1) koeficijent za vodeći član (za x²) je +1,
2) možete pronaći dva cijela broja (sa predznacima ili dva relativna cijela broja) takva da je njihov zbir jednak koeficijentu x na prvi stepen i njihov proizvod je jednak članu bez x (gdje nema slova x na sve).
Primjeri. 1. x² + 5x + 6; Lako je mentalno pronaći dva broja (sa predznacima) tako da je njihov zbir jednak +5 (koeficijent x) i da je njihov proizvod = +6 (član bez x) - ovi brojevi su: +2 i + 3 [u stvari, +2 + 3 = +5 i (+2) ∙ (+3) = +6]. Koristeći ova dva broja, termin +5x zamjenjujemo sa dva člana, i to: +2x + 3x (naravno, +2x + 3x = +5x); tada će naš tehnički termin biti umjetno pretvoren u četveročlani x² + 2x + 3x + 6. Primijenimo sada tehniku grupisanja na njega, dodjeljujući prva dva člana jednoj grupi, a posljednja dva drugoj:
x² + 5x + 6 = x² + 2x + 3x + 6 = x (x + 2) + 3 (x + 2) = (x + 2) (x + 3).
U prvoj grupi smo izvadili x iz zagrade, au drugoj +3 dobili smo dva člana koji su imali zajednički faktor (x + 2), koji smo također izvadili iz zagrade, i naš trinom x² + 5x + 6 rastaviti na 2 linearna faktora: x + 2 i x + 3.
2. x² – x – 12. Ovdje morate pronaći dva broja (relativna) tako da je njihov zbir jednak –1 i da njihov proizvod bude jednak –12. Ovi brojevi su: –4 i +3.
Provjerite: –4 + 3 = –1; (–4) (+3) = –12. Koristeći ove brojeve, zamjenjujemo pojam –x sa dva člana: –x = –4x + 3x, – dobijamo:
x² – x – 12 = x² – 4x + 3x – 12 = x (x – 4) + 3 (x – 4) = (x – 4) (x + 3).
3. x² – 7x + 6; ovdje su traženi brojevi: –6 i –1. [Provjera: –6 + (–1) = –7; (–6) (–1) = +6].
x² – 7x + 6 = x² – 6x – x + 6 = x (x – 6) – (x – 6) = (x – 6) (x – 1).
Ovdje su članovi druge grupe –x + 6 morali biti stavljeni u zagrade, sa znakom minus ispred njih.
4. x² + 8x – 48. Ovdje morate pronaći dva broja tako da njihov zbir bude +8, a proizvod –48. Pošto proizvod mora imati predznak minus, onda traženi brojevi moraju imati različite predznake, pošto zbir naših brojeva ima predznak +, tada apsolutna vrijednost mora biti više pozitivnih brojeva. Unfolding aritmetički broj 48 sa dva faktora (a to se može uraditi na različite načine), dobijamo: 48 = 1 ∙ 48 = 2 ∙ 24 = 3 ∙ 16 = 4 ∙ 12 = 6 ∙ 8. Iz ovih proširenja lako je izabrati ono koji odgovara našim zahtjevima, odnosno: 48 = 4 ∙ 12. Tada su naši brojevi: +12 i –4. Ostalo je jednostavno:
x² + 8x – 48 = x² + 12x – 4x – 48 = x (x + 12) – 4 (x + 12) = (x + 12) (x – 4).
5. x² + 7x – 12. Ovdje morate pronaći 2 broja tako da njihov zbir bude +7, a proizvod = –12; 12 = 1 ∙ 12 = 2 ∙ 6 = 3 ∙ 4. Očigledno, 3 i 4 bi bili prikladni brojevi, ali se moraju uzeti s različitim predznacima tako da im je proizvod jednak –12, a onda njihov zbir ni u kom slučaju ne smije biti +7 [–3 + (+4) = +1, +3 + (–4) = –1]. Druge faktorizacije također ne daju tražene brojeve; Stoga dolazimo do zaključka da još nismo u mogućnosti da ove kvadratne trinome dekomponujemo na linearne faktore, jer naša tehnika nije primenljiva na nju (ne zadovoljava drugi od uslova koji su postavljeni na početku).
U ovoj lekciji naučit ćemo kako razložiti kvadratne trinome u linearne faktore. Da bismo to učinili, moramo se sjetiti Vietine teoreme i njene obrnutosti. Ova vještina će nam pomoći da brzo i prikladno proširimo kvadratne trinome u linearne faktore, a također će pojednostaviti redukciju razlomaka koji se sastoje od izraza.
Dakle, vratimo se na kvadratnu jednačinu, gdje je .
Ono što imamo na lijevoj strani naziva se kvadratni trinom.
Teorema je tačna: Ako su korijeni kvadratnog trinoma, onda vrijedi identitet
Gdje je vodeći koeficijent, korijeni su jednadžbe.
Dakle, imamo kvadratnu jednačinu - kvadratni trinom, gdje se korijeni kvadratne jednadžbe nazivaju i korijeni kvadratnog trinoma. Stoga, ako imamo korijene kvadratnog trinoma, onda se ovaj trinom može razložiti na linearne faktore.
dokaz:
Dokaz ovu činjenicu se izvodi pomoću Vietine teoreme, o kojoj smo raspravljali u prethodnim lekcijama.
Prisjetimo se šta nam kaže Vietina teorema:
Ako su korijeni kvadratnog trinoma za koje , Tada .
Iz ove teoreme slijedi sljedeća izjava:
Vidimo da, prema Vietinoj teoremi, tj. zamjenom ovih vrijednosti u gornju formulu, dobijamo sljedeći izraz
Q.E.D.
Podsjetimo da smo dokazali teoremu da ako su korijeni kvadratnog trinoma, onda je proširenje važeće.
Sada se prisjetimo primjera kvadratne jednadžbe, kojoj smo odabrali korijene koristeći Vietin teorem. Iz ove činjenice možemo dobiti sljedeću jednakost zahvaljujući dokazanoj teoremi:
Sada provjerimo ispravnost ove činjenice jednostavnim otvaranjem zagrada:
Vidimo da smo ispravno faktorizirali i svaki trinom, ako ima korijen, može se faktorizirati prema ovoj teoremi u linearne faktore prema formuli
Međutim, hajde da proverimo da li je takva faktorizacija moguća za bilo koju jednačinu:
Uzmimo, na primjer, jednadžbu . Prvo, provjerimo diskriminirajući znak
I zapamtimo da da bi se ispunila teorema koju smo naučili, D mora biti veći od 0, tako da je u ovom slučaju faktorizacija prema teoremi koju smo naučili nemoguća.
Stoga formuliramo novu teoremu: ako kvadratni trinom nema korijen, onda se ne može rastaviti na linearne faktore.
Dakle, pogledali smo Vietin teorem, mogućnost dekomponovanja kvadratnog trinoma na linearne faktore, a sada ćemo riješiti nekoliko problema.
Zadatak br. 1
U ovoj grupi ćemo zapravo rješavati problem obrnuto od postavljenog. Imali smo jednačinu i našli smo njene korijene rastavljajući je na faktore. Ovdje ćemo učiniti suprotno. Recimo da imamo korijene kvadratne jednadžbe
Inverzni problem je sljedeći: napišite kvadratnu jednačinu koristeći njene korijene.
Postoje 2 načina za rješavanje ovog problema.
Pošto su korijeni jednadžbe, onda ![]() je kvadratna jednadžba čiji su korijeni dati brojevi. Sada otvorimo zagrade i provjerimo:
je kvadratna jednadžba čiji su korijeni dati brojevi. Sada otvorimo zagrade i provjerimo:
![]()
Ovo je bio prvi način na koji smo kreirali kvadratnu jednačinu date korene, koji nema druge korijene, budući da svaka kvadratna jednadžba ima najviše dva korijena.
Ova metoda uključuje korištenje obrnuta teorema Vieta.
Ako su korijeni jednadžbe, onda oni zadovoljavaju uvjet da .
Za redukovanu kvadratnu jednačinu ![]() , , tj. u ovom slučaju, i .
, , tj. u ovom slučaju, i .
Tako smo kreirali kvadratnu jednačinu koja ima date korijene.
Zadatak br. 2
Potrebno je smanjiti frakciju.
Imamo trinom u brojniku i trinom u nazivniku, a trinomi se mogu ili ne moraju faktorizirati. Ako su i brojnik i imenilac rastavljeni na faktore, onda među njima mogu postojati jednaki faktori koji se mogu smanjiti.
Prije svega, morate rastaviti brojilac na faktore.
Prvo morate provjeriti da li se ova jednačina može faktorizirati, hajde da nađemo diskriminanta. Budući da , predznak ovisi o proizvodu (mora biti manji od 0), u u ovom primjeru, tj. zadata jednačina ima korene.
![]()
Za rješavanje koristimo Vietinu teoremu:

U ovom slučaju, budući da imamo posla s korijenima, bit će prilično teško jednostavno odabrati korijene. Ali vidimo da su koeficijenti izbalansirani, odnosno, ako pretpostavimo da je , i zamijenimo ovu vrijednost u jednačinu, dobićemo sljedeći sistem: , tj. 5-5=0. Stoga smo odabrali jedan od korijena ove kvadratne jednadžbe.
Drugi korijen ćemo tražiti zamjenom onoga što je već poznato u sistem jednačina, na primjer, , tj. .
Dakle, pronašli smo oba korijena kvadratne jednadžbe i možemo zamijeniti njihove vrijednosti u originalnu jednadžbu da bismo je faktorirali:
![]()
Sjetimo se prvobitnog problema, trebali smo smanjiti razlomak.
Pokušajmo riješiti problem zamjenom .
Ne treba zaboraviti da u ovom slučaju imenilac ne može biti jednak 0, tj. , .
Ako su ovi uvjeti ispunjeni, onda smo originalni razlomak sveli na oblik .
Problem br. 3 (zadatak sa parametrom)
Pri kojim vrijednostima parametra je zbir korijena kvadratne jednadžbe
Ako korijeni ove jednadžbe postoje, onda ![]() , pitanje: kada.
, pitanje: kada.
KVADRAT TRIPLE III
§ 54. Dekompozicija kvadratnog trinoma na linearne faktore
U ovom dijelu ćemo razmotriti sljedeće pitanje: u kojem slučaju je kvadratni trinom sjekira 2 + bx + c može se predstaviti kao proizvod
(a 1 x+b 1) (a 2 x+b 2)
dva linearna relativna X množitelji sa realnim koeficijentima a 1 , b 1 , a 2 , b 2 (a 1 =/=0, a 2 =/=0) ?
1. Pretpostavimo da je dati kvadratni trinom sjekira 2 + bx + c predstavimo ga u obliku
sjekira 2 + bx + c = (a 1 x+b 1) (a 2 x+b 2). (1)
Desna strana formule (1) nestaje kada X = - b 1 / a 1 i X = - b 2 / a 2 (a 1 i a 2 nisu jednaki nuli po uslovu). Ali u ovom slučaju brojevi jesu b 1 / a 1 i - b 2 / a 2 su korijeni jednadžbe
sjekira 2 + bx + c = 0.
Dakle, diskriminant kvadratnog trinoma sjekira 2 + bx + c mora biti nenegativna.
2. Obrnuto, pretpostavimo da je diskriminant D = b 2 - 4ac kvadratni trinom sjekira 2 + bx + c nenegativan. Tada ovaj trinom ima realne korijene x 1 i x 2. Koristeći Vietinu teoremu, dobijamo:
sjekira 2 + bx + c =A (x 2 + b / a X + c / a ) = A [x 2 - (x 1 + x 2) X + x 1 x 2 ] =
= A [(x 2 - x 1 x ) - (x 2 x - x 1 x 2)] = A [X (X - x 1) - x 2 (X - x 1) =
=a (X - x 1)(X - x 2).
sjekira 2 + bx + c = a (X - x 1)(X - x 2), (2)
Gdje x 1 i x 2 - korijeni trinoma sjekira 2 + bx + c . Koeficijent A može se pripisati jednom od dva linearna faktora, na primjer,
a (X - x 1)(X - x 2) = (ah - sjekira 1)(X - x 2).
Ali to znači da je u slučaju koji se razmatra kvadratni trinom sjekira 2 + bx + c predstavljaju ga kao proizvod dva linearna faktora sa realnim koeficijentima.
Kombinujući rezultate dobijene u paragrafima 1 i 2, dolazimo do sledeće teoreme.
Teorema. Kvadratni trinom sjekira 2 + bx + c tada i samo tada se može predstaviti kao proizvod dva linearna faktora sa realnim koeficijentima,
sjekira 2 + bx + c = (ah - sjekira 1)(X - x 2),
kada je diskriminant ovog kvadratnog trinoma nenegativan (tj. kada ovaj trinom ima realne korijene).
Primjer 1. Linearni faktor 6 x 2 - X -1.
Korijeni ovog kvadratnog trinoma su jednaki x 1 = 1/2 i x 2 = - 1 / 3 .
Dakle, prema formuli (2)
6x 2 - X -1 = 6 (X - 1 / 2)(X + 1 / 3) = (2X - 1) (3x + 1).
Primjer 2. Linearna faktorizacija x 2 + X + 1. Diskriminanta ovog kvadratnog trinoma je negativna:
D = 1 2 - 4 1 1 = - 3< 0.
Stoga se ovaj kvadratni trinom ne može proširiti u linearne faktore sa realnim koeficijentima.
Vježbe
Faktori sljedeće izraze u linearne faktore (br. 403 - 406):
403. 6x 2 - 7X + 2. 405. x 2 - X + 1.
404. 2x 2 - 7Oh + 6A 2 . 406. x 2 - 3Oh + 2A 2 - ab - b 2 .
Smanjite razlomke (br. 407, 408):
Riješite jednačine: