Средняя линия фигур в планиметрии - отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Средняя линия треугольника
Свойства
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
- Площадь и, соответственно, и объём отсекаемого средней линией треугольника равна 1/4 от площади и, соотвественно, объёму от всего данного треугольника.
Средняя линия четырёхугольника
Средняя линия четырёхугольника - отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника - вершины параллелограмма . Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона ;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода . Средние линии второго рода - четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона .
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции
Средняя линия трапеции
Средняя линия трапеции - отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: E F = A D + B C 2 {\displaystyle EF={\frac {AD+BC}{2}}} , где AD и BC - основания трапеции.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:

Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.

Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:

Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.

Вычисляем по формуле:

27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:

Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:

Таким образом DC=6. Вычисляем:

27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.

Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.

Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:

Второе уравнение уже можно записать в виде:

27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.

Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
![]()
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:

Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:

Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD , если стороны квадратных клеток равны 1.

Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD - основания, AD и BC - боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема
: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные -- боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции -- это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ -- средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ - середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
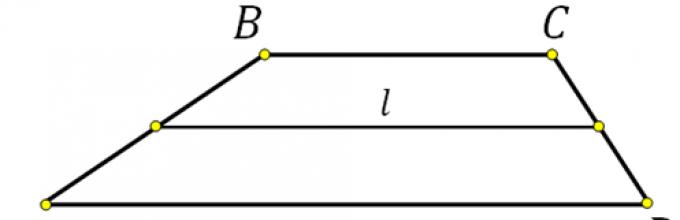
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).

Рисунок 2.
Так как $AD$ и $BC$ - расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ -- радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ - трапеция, а $OH$ - ее средняя линия. По теореме 1, получаем
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 - МЕТ = 180 0 - КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.