ΕΝΑ)Λύστε την εξίσωση 2(\sin x-\cos x)=tgx-1.
σι) \αριστερά[ \frac(3\pi )2;\,3\pi \δεξιά].
Δείξε λύσηΛύση
ΕΝΑ)Ανοίγοντας τις αγκύλες και μετακινώντας όλους τους όρους στην αριστερή πλευρά, παίρνουμε την εξίσωση 1+2 \sin x-2 \cos x-tg x=0. Λαμβάνοντας υπόψη ότι \cos x \neq 0, ο όρος 2 \sin x μπορεί να αντικατασταθεί από 2 tan x \cos x, λαμβάνουμε την εξίσωση 1+2 tg x \cos x-2 \cos x-tg x=0,που ομαδοποιώντας μπορεί να αναχθεί στη μορφή (1-tg x)(1-2 \cos x)=0.
1) 1-tg x=0, μαύρισμα x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;
2) 1-2 \cos x=0, \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.
σι)Με τη χρήση κύκλος αριθμώνεπιλέξτε τις ρίζες που ανήκουν στο διάστημα \αριστερά[ \frac(3\pi )2;\, 3\pi \δεξιά].
x_1=\frac\pi 4+2\pi =\frac(9\pi )4,
x_2=\frac\pi 3+2\pi =\frac(7\pi )3,
x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
Απάντηση
ΕΝΑ) \frac\pi 4+\pi n, \pm\frac\pi 3+2\pi n, n \in \mathbb Z;
σι) \frac(5\pi )3, \frac(7\pi )3, \frac(9\pi )4.
Κατάσταση
ΕΝΑ)Λύστε την εξίσωση (2\sin ^24x-3\cos 4x)\cdot \sqrt (tgx)=0.
σι)Να αναφέρετε τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα \left(0;\,\frac(3\pi )2\right] ;
Δείξε λύσηΛύση
ΕΝΑ) ODZ: \begin(περιπτώσεις) tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end(περιπτώσεις)
Η αρχική εξίσωση στο ODZ είναι ισοδύναμη με ένα σύνολο εξισώσεων
\left[\!\!\begin(array)(l) 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \end(πίνακας)\δεξιά.
Ας λύσουμε την πρώτη εξίσωση. Για να γίνει αυτό θα κάνουμε μια αντικατάσταση \cos 4x=t, t \σε [-1; 1].Τότε \sin^24x=1-t^2. Παίρνουμε:
2(1-t^2)-3t=0,
2t^2+3t-2=0,
t_1=\frac12, t_2=-2, t_2\notin [-1; 1].
\cos 4x=\frac12,
4x=\pm\frac\pi 3+2\pi n,
x=\pm \frac\pi (12)+\frac(\pi n)2, n \in \mathbb Z.
Ας λύσουμε τη δεύτερη εξίσωση.
tg x=0,\, x=\pi k, k \in \mathbb Z.
Με βοήθεια κύκλος μονάδαςΑς βρούμε λύσεις που να ικανοποιούν την ΟΔΖ.

Το σύμβολο «+» σηματοδοτεί το 1ο και 3ο τέταρτο, στα οποία tg x>0.
Παίρνουμε: x=\pi k, k \in \mathbb Z; x=\frac\pi (12)+\pi n, n \in \mathbb Z; x=\frac(5\pi )(12)+\pi m, m \in \mathbb Z.
σι)Ας βρούμε τις ρίζες που ανήκουν στο διάστημα \αριστερά(0;\,\frac(3\pi )2\δεξιά].
.png)
x=\frac\pi (12), x=\frac(5\pi )(12); x=\pi ; x=\frac(13\pi )(12); x=\frac(17\pi )(12).
Απάντηση
ΕΝΑ) \pi k, k \in \mathbb Z; \frac\pi (12)+\pi n, n \in \mathbb Z; \frac(5\pi )(12)+\pi m, m \in \mathbb Z.
σι) \πι; \frac\pi (12); \frac(5\pi )(12); \frac(13\pi )(12); \frac(17\pi )(12).
Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ" Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.
Κατάσταση
ΕΝΑ)Λύστε την εξίσωση: \cos ^2x+\cos ^2\frac\pi 6=\cos ^22x+\sin ^2\frac\pi 3;
σι)Καταγράψτε όλες τις ρίζες που ανήκουν στο διάστημα \left(\frac(7\pi )2;\,\frac(9\pi )2\right].
Δείξε λύσηΛύση
ΕΝΑ)Επειδή \sin \frac\pi 3=\cos \frac\pi 6,Οτι \sin ^2\frac\pi 3=\cos ^2\frac\pi 6,Που σημαίνει, δεδομένη εξίσωσηείναι ισοδύναμη με την εξίσωση \cos^2x=\cos ^22x, η οποία, με τη σειρά της, είναι ισοδύναμη με την εξίσωση \cos^2x-\cos ^2 2x=0.
Αλλά \cos ^2x-\cos ^22x= (\cos x-\cos 2x)\cdot (\cos x+\cos 2x)Και
\cos 2x=2 \cos ^2 x-1, οπότε η εξίσωση γίνεται
(\cos x-(2 \cos ^2 x-1))\,\cdot(\cos x+(2 \cos ^2 x-1))=0,
(2 \cos ^2 x-\cos x-1)\,\cdot (2 \cos ^2 x+\cos x-1)=0.
Τότε είτε 2 \cos ^2 x-\cos x-1=0, είτε 2 \cos ^2 x+\cos x-1=0.
Επίλυση της πρώτης εξίσωσης ως τετραγωνική εξίσωσησε σχέση με το \cos x, παίρνουμε:
(\cos x)_(1,2)=\frac(1\pm\sqrt 9)4=\frac(1\pm3)4.Επομένως είτε \cos x=1 είτε \cos x=-\frac12.Αν \cos x=1, τότε x=2k\pi , k \in \mathbb Z. Αν \cos x=-\frac12,Οτι x=\pm \frac(2\pi )3+2s\pi, s \in \mathbb Z.
Ομοίως, λύνοντας τη δεύτερη εξίσωση, παίρνουμε είτε \cos x=-1 είτε \cos x=\frac12.Αν \cos x=-1, τότε οι ρίζες x=\pi +2m\pi , m \in \mathbb Z.Αν \cos x=\frac12,Οτι x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.
Ας συνδυάσουμε τις λύσεις που προέκυψαν:
x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.
σι)Ας επιλέξουμε τις ρίζες που εμπίπτουν σε ένα δεδομένο διάστημα χρησιμοποιώντας έναν κύκλο αριθμών.

Παίρνουμε: x_1 =\frac(11\pi )3, x_2=4\pi, x_3 =\frac(13\pi )3.
Απάντηση
ΕΝΑ) m\pi, m\in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;
σι) \frac(11\pi )3, 4\pi, \frac(13\pi )3.
Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova.
Κατάσταση
ΕΝΑ)Λύστε την εξίσωση 10\cos ^2\frac x2=\frac(11+5ctg\left(\dfrac(3\pi )2-x\right) )(1+tgx).
σι)Να αναφέρετε τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα \left(-2\pi ; -\frac(3\pi)2\δεξιά).
Δείξε λύσηΛύση
ΕΝΑ) 1. Σύμφωνα με τον τύπο μείωσης, ctg\left(\frac(3\pi )2-x\right) =tgx.Το πεδίο ορισμού της εξίσωσης θα είναι τέτοιες τιμές του x τέτοιες ώστε \cos x \neq 0 και tan x \neq -1. Ας μετατρέψουμε την εξίσωση χρησιμοποιώντας τον τύπο συνημιτόνου διπλής γωνίας 2 \cos ^2 \frac x2=1+\cos x.Παίρνουμε την εξίσωση: 5(1+\cos x) =\frac(11+5tgx)(1+tgx).
σημειώσε ότι \frac(11+5tgx)(1+tgx)= \frac(5(1+tgx)+6)(1+tgx)= 5+\frac(6)(1+tgx),οπότε η εξίσωση γίνεται: 5+5 \cos x=5 +\frac(6)(1+tgx).Από εδώ \cos x =\frac(\dfrac65)(1+tgx), \cos x+\sin x =\frac65.
2. Μετασχηματίστε το \sin x+\cos x χρησιμοποιώντας τον τύπο αναγωγής και τον τύπο του αθροίσματος των συνημιτόνων: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left(x-\frac\pi 4\right) = \frac65.
Από εδώ \cos \left(x-\frac\pi 4\right) =\frac(3\sqrt 2)5.Που σημαίνει, x-\frac\pi 4= arc\cos \frac(3\sqrt 2)5+2\pi k, k \in \mathbb Z,
ή x-\frac\pi 4= -arc\cos \frac(3\sqrt 2)5+2\pi t, t \in \mathbb Z.
Να γιατί x=\frac\pi 4+arc\cos \frac(3\sqrt 2)5+2\pi k,k \in \mathbb Z,
ή x =\frac\pi 4-arc\cos \frac(3\sqrt 2)5+2\pi t,t \in \mathbb Z.
Οι τιμές του x που βρέθηκαν ανήκουν στον τομέα ορισμού.
σι)Ας μάθουμε πρώτα πού πέφτουν οι ρίζες της εξίσωσης σε k=0 και t=0. Αυτοί θα είναι αριθμοί ανάλογα a=\frac\pi 4+arccos \frac(3\sqrt 2)5Και b=\frac\pi 4-arccos \frac(3\sqrt 2)5.
1. Ας αποδείξουμε τη βοηθητική ανισότητα:
\frac(\sqrt 2)(2)<\frac{3\sqrt 2}2<1.
Πραγματικά, \frac(\sqrt 2)(2)=\frac(5\sqrt 2)(10)<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.
Σημειώστε επίσης ότι \left(\frac(3\sqrt 2)5\right) ^2=\frac(18)(25)<1^2=1, Που σημαίνει \frac(3\sqrt 2)5<1.
2. Από τις ανισότητες (1) Με την ιδιότητα συνημιτόνου τόξου παίρνουμε:
τόξο 1 0 Από εδώ \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,
0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,
0 Επίσης, -\frac\pi 4 0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5<
0 Για k=-1 και t=-1 λαμβάνουμε τις ρίζες της εξίσωσης a-2\pi και b-2\pi. \Bigg(a-2\pi =-\frac74\pi +arccos \frac(3\sqrt 2)5,\, b-2\pi =-\frac74\pi -arccos \frac(3\sqrt 2)5\Bigg).Εν -2\pi 2\pi Για άλλες τιμές των k και t, οι ρίζες της εξίσωσης δεν ανήκουν στο δεδομένο διάστημα. Πράγματι, αν k\geqslant 1 και t\geqslant 1, τότε οι ρίζες είναι μεγαλύτερες από 2\pi. Αν k\leqslant -2 και t\leqslant -2, τότε οι ρίζες είναι μικρότερες -\frac(7\pi )2. ΕΝΑ) \frac\pi4\pm arccos\frac(3\sqrt2)5+2\pi k, k\in\mathbb Z; σι) -\frac(7\pi)4\pm arccos\frac(3\sqrt2)5. Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova. ΕΝΑ)Λύστε την εξίσωση \sin \left(\frac\pi 2+x\right) =\sin (-2x). σι)Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα ; ΕΝΑ)Ας μετατρέψουμε την εξίσωση: \cos x =-\sin 2x, \cos x+2 \sin x \cos x=0, \cos x(1+2 \sin x)=0, \cos x=0, x =\frac\pi 2+\pi n, n\in \mathbb Z; 1+2 \sin x=0, \sin x=-\frac12, x=(-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z. σι)Βρίσκουμε τις ρίζες που ανήκουν στο τμήμα χρησιμοποιώντας τον μοναδιαίο κύκλο. Το υποδεικνυόμενο διάστημα περιέχει έναν μόνο αριθμό \frac\pi 2. ΕΝΑ) \frac\pi 2+\pi n, n \in \mathbb Z; (-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z; σι) \frac\pi 2. Πηγή: «Μαθηματικά. Προετοιμασία για την Ενιαία Κρατική Εξέταση 2017. Επίπεδο προφίλ." Εκδ. F. F. Lysenko, S. Yu. Kulabukhova. Που σημαίνει, \sin x \neq 1. Διαιρέστε και τις δύο πλευρές της εξίσωσης με έναν παράγοντα (\sin x-1),διαφορετικό από το μηδέν. Παίρνουμε την εξίσωση \frac 1(1+\cos 2x)=\frac 1(1+\cos (\pi +x)),ή εξίσωση 1+\cos 2x=1+\cos (\pi +x).Εφαρμόζοντας τον τύπο αναγωγής στην αριστερή πλευρά και τον τύπο αναγωγής στα δεξιά, λαμβάνουμε την εξίσωση 2 \cos ^2 x=1-\cos x.Αυτή η εξίσωση είναι με αντικατάσταση \cos x=t,Οπου -1 \leqslant t \leqslant 1μειώστε το στο τετράγωνο: 2t^2+t-1=0,των οποίων οι ρίζες t_1=-1Και t_2=\frac12.Επιστρέφοντας στη μεταβλητή x, παίρνουμε \cos x = \frac12ή \cos x=-1,που x=\frac \pi 3+2\pi m, m\in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z. σι)Ας λύσουμε τις ανισότητες 1) -\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2, 2) -\frac(3\pi )2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi (2,) 3) -\frac(3\pi )2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2, 1)
-\frac(3\pi )2 \leqslant \frac(\pi )3+2\pi m \leqslant -\frac \pi 2, -\frac32\leqslant \frac13+2m \leqslant -\frac12 -\frac(11)6 \leqslant 2m\leqslant -\frac56, -\frac(11)(12) \leqslant m \leqslant -\frac5(12). \αριστερά [-\frac(11)(12);-\frac5(12)\right]. 2)
-\frac (3\pi) 2 \leqslant -\frac(\pi )3+2\pi n \leqslant -\frac(\pi )(2), -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12, -\frac76 \leqslant 2n \leqslant -\frac1(6), -\frac7(12) \leqslant n \leqslant -\frac1(12). Δεν υπάρχουν ακέραιοι αριθμοί στην περιοχή \left[ -\frac7(12) ; -\frac1(12)\right]. 3)
-\frac(3\pi )2 \leqslant \pi +2\pi k\leqslant -\frac(\pi )2, -\frac32 \leqslant 1+2k\leqslant -\frac12, -\frac52 \leqslant 2k \leqslant -\frac32, -\frac54 \leqslant k \leqslant -\frac34. Αυτή η ανισότητα ικανοποιείται από k=-1 και μετά x=-\pi. ΕΝΑ) \frac \pi 3+2\pi m; -\frac \pi 3+2\pi n; \pi +2\pi k, Μ, n, k \in \mathbb Z; σι) -\πι . Σε αυτό το άρθρο θα προσπαθήσω να εξηγήσω 2 τρόπους επιλέγοντας ρίζες σε μια τριγωνομετρική εξίσωση: χρησιμοποιώντας ανισώσεις και χρησιμοποιώντας τον τριγωνομετρικό κύκλο. Ας προχωρήσουμε κατευθείαν σε ένα ενδεικτικό παράδειγμα και θα καταλάβουμε πώς λειτουργούν τα πράγματα. Α) Λύστε την εξίσωση sqrt(2)cos^2x=sin(Pi/2+x) Ας λύσουμε το σημείο α. Ας χρησιμοποιήσουμε τον τύπο αναγωγής για sinine sin(Pi/2+x) = cos(x) Sqrt(2)cos^2x = cosx Sqrt(2)cos^2x - cosx = 0 Cosx(sqrt(2)cosx - 1) = 0 X1 = Pi/2 + Pin, n ∈ Z Sqrt(2)cosx - 1 = 0 Cosx = 1/sqrt(2) Cosx = sqrt(2)/2 X2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z X2 = Pi/4 + 2Pin, n ∈ Z Ας λύσουμε το σημείο β. 1) Επιλογή ριζών με χρήση ανισοτήτων Εδώ όλα γίνονται απλά, αντικαθιστούμε τις ρίζες που προκύπτουν στο διάστημα που μας δίνεται [-7Pi/2; -2Pi], βρείτε ακέραιες τιμές για n. 7Pi/2 μικρότερο ή ίσο με Pi/2 + Pin μικρότερο ή ίσο με -2Pi Αμέσως χωρίζουμε τα πάντα με το Pi 7/2 μικρότερο ή ίσο με 1/2 + n μικρότερο ή ίσο με -2 7/2 - 1/2 μικρότερο ή ίσο με n μικρότερο ή ίσο με -2 - 1/2 4 μικρότερο ή ίσο με n μικρότερο ή ίσο με -5/2 Οι ακέραιοι n σε αυτό το διάστημα είναι -4 και -3. Αυτό σημαίνει ότι οι ρίζες που ανήκουν σε αυτό το διάστημα θα είναι Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2 Ομοίως κάνουμε δύο ακόμη ανισότητες 7Pi/2 μικρότερο ή ίσο με Pi/4 + 2Pin μικρότερο ή ίσο με -2Pi Δεν υπάρχουν ολόκληρα n σε αυτό το διάστημα 7Pi/2 μικρότερο ή ίσο με -Pi/4 + 2Pin μικρότερο ή ίσο με -2Pi Ένας ακέραιος n σε αυτό το διάστημα είναι -1. Αυτό σημαίνει ότι η επιλεγμένη ρίζα σε αυτό το διάστημα είναι -Pi/4 + 2Pi*(-1) = -9Pi/4. Άρα η απάντηση στο σημείο β: -7Pi/2, -5Pi/2, -9Pi/4 2) Επιλογή ριζών με χρήση τριγωνομετρικού κύκλου Για να χρησιμοποιήσετε αυτήν τη μέθοδο, πρέπει να κατανοήσετε πώς λειτουργεί αυτός ο κύκλος. Θα προσπαθήσω να εξηγήσω με απλή γλώσσα πώς το καταλαβαίνω αυτό. Νομίζω ότι στα σχολεία, κατά τη διάρκεια των μαθημάτων της άλγεβρας, το θέμα αυτό εξηγούνταν πολλές φορές με έξυπνα λόγια του δασκάλου, στα σχολικά βιβλία υπήρχαν πολύπλοκες διατυπώσεις. Προσωπικά, το καταλαβαίνω ως έναν κύκλο που μπορεί να περιηγηθεί άπειρες φορές, αυτό εξηγείται από το γεγονός ότι οι συναρτήσεις ημιτονοειδούς και συνημιτόνου είναι περιοδικές. Ας γυρίσουμε αριστερόστροφα Ας πάμε γύρω 2 φορές αριστερόστροφα Ας πάμε γύρω 1 φορά δεξιόστροφα (οι τιμές θα είναι αρνητικές) Ας επιστρέψουμε στην ερώτησή μας, πρέπει να επιλέξουμε ρίζες στο διάστημα [-7Pi/2; -2 Pi] Για να φτάσετε στους αριθμούς -7Pi/2 και -2Pi πρέπει να περιηγηθείτε στον κύκλο αριστερόστροφα δύο φορές. Για να βρείτε τις ρίζες της εξίσωσης σε αυτό το διάστημα, πρέπει να υπολογίσετε και να αντικαταστήσετε. Θεωρήστε x = Pi/2 + Pin. Τι θα πρέπει να είναι περίπου το n για το x να είναι κάπου σε αυτό το εύρος; Αντικαθιστούμε, ας πούμε -2, παίρνουμε Pi/2 - 2Pi = -3Pi/2, προφανώς αυτό δεν περιλαμβάνεται στο μεσοδιάστημά μας, οπότε παίρνουμε λιγότερο από -3, Pi/2 - 3Pi = -5Pi/2, αυτό είναι κατάλληλο, ας προσπαθήσουμε ξανά -4 , Pi/2 - 4Pi = -7Pi/2, επίσης κατάλληλο. Συλλογιζόμενοι ομοίως για τα Pi/4 + 2Pin και -Pi/4 + 2Pin, βρίσκουμε μια άλλη ρίζα -9Pi/4. Σύγκριση δύο μεθόδων. Η πρώτη μέθοδος (χρησιμοποιώντας ανισότητες) είναι πολύ πιο αξιόπιστη και πολύ πιο εύκολα κατανοητή, αλλά αν ασχολείστε πραγματικά με τον τριγωνομετρικό κύκλο και τη δεύτερη μέθοδο επιλογής, τότε η επιλογή των ριζών θα είναι πολύ πιο γρήγορη, μπορείτε να εξοικονομήσετε περίπου 15 λεπτά στην εξέταση . α) Λύστε την εξίσωση: . β) Να βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα. Αυτό το μάθημα εξετάζει ένα παράδειγμα επίλυσης τριγωνομετρικής εξίσωσης, το οποίο μπορεί να χρησιμοποιηθεί ως παράδειγμα για την επίλυση προβλημάτων τύπου C1 κατά την προετοιμασία για την Ενιαία Κρατική Εξέταση στα μαθηματικά. Πρώτα απ 'όλα, προσδιορίζεται το εύρος της συνάρτησης - όλες οι έγκυρες τιμές του ορίσματος. Στη συνέχεια, κατά τη διάρκεια της λύσης, η συνάρτηση τριγωνομετρικού ημιτόνου μετατρέπεται σε συνημίτονο χρησιμοποιώντας τον τύπο αναγωγής. Στη συνέχεια, όλοι οι όροι της εξίσωσης μεταφέρονται στην αριστερή πλευρά της, όπου ο κοινός παράγοντας αφαιρείται από αγκύλες. Κάθε παράγοντας είναι ίσος με μηδέν, κάτι που μας επιτρέπει να προσδιορίσουμε τις ρίζες της εξίσωσης. Στη συνέχεια, χρησιμοποιώντας τη μέθοδο των στροφών, προσδιορίζονται οι ρίζες που ανήκουν σε ένα δεδομένο τμήμα. Για να γίνει αυτό, στον κατασκευασμένο κύκλο μονάδας, σημειώνεται μια στροφή από το αριστερό περίγραμμα ενός δεδομένου τμήματος προς τα δεξιά. Στη συνέχεια, οι ρίζες που βρέθηκαν στον κύκλο μονάδας συνδέονται με τμήματα στο κέντρο του και προσδιορίζονται τα σημεία στα οποία αυτά τα τμήματα τέμνουν τη στροφή. Αυτά τα σημεία τομής είναι η επιθυμητή απάντηση στο δεύτερο μέρος του προβλήματος. Μπορείτε να παραγγείλετε μια αναλυτική λύση στο πρόβλημά σας!!! Μια ισότητα που περιέχει έναν άγνωστο κάτω από το πρόσημο μιας τριγωνομετρικής συνάρτησης («sin x, cos x, tan x» ή «ctg x») ονομάζεται τριγωνομετρική εξίσωση και είναι οι τύποι τους που θα εξετάσουμε περαιτέρω. Οι απλούστερες εξισώσεις είναι «sin x=a, cos x=a, tg x=a, ctg x=a», όπου «x» είναι η γωνία που πρέπει να βρεθεί, «a» είναι οποιοσδήποτε αριθμός. Ας γράψουμε τους τύπους ρίζας για καθένα από αυτά. 1. Εξίσωση `sin x=a`. Για το `|a|>1` δεν έχει λύσεις. Όταν `|α| Το \leq 1` έχει άπειρο αριθμό λύσεων. Τύπος ρίζας: `x=(-1)^n arcsin a + \pi n, n \in Z` 2. Εξίσωση `cos x=a` Για `|a|>1` - όπως στην περίπτωση του ημιτονοειδούς, δεν έχει λύσεις μεταξύ των πραγματικών αριθμών. Όταν `|α| Το \leq 1` έχει άπειρο αριθμό λύσεων. Τύπος ρίζας: `x=\pm arccos a + 2\pi n, n \in Z` Ειδικές περιπτώσεις για ημίτονο και συνημίτονο σε γραφήματα. 3. Εξίσωση `tg x=a` Έχει άπειρο αριθμό λύσεων για οποιεσδήποτε τιμές του 'a'. Τύπος ρίζας: `x=arctg a + \pi n, n \in Z` 4. Εξίσωση `ctg x=a` Έχει επίσης έναν άπειρο αριθμό λύσεων για οποιεσδήποτε τιμές του 'a'. Τύπος ρίζας: `x=arcctg a + \pi n, n \in Z` Για ημιτονοειδή: Η επίλυση οποιασδήποτε τριγωνομετρικής εξίσωσης αποτελείται από δύο στάδια: Ας δούμε τις κύριες μεθόδους λύσης χρησιμοποιώντας παραδείγματα. Αυτή η μέθοδος περιλαμβάνει την αντικατάσταση μιας μεταβλητής και την αντικατάστασή της σε μια ισότητα. Παράδειγμα. Λύστε την εξίσωση: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0` `2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`, κάντε μια αντικατάσταση: `cos(x+\frac \pi 6)=y`, μετά `2y^2-3y+1=0`, βρίσκουμε τις ρίζες: `y_1=1, y_2=1/2`, από τις οποίες ακολουθούν δύο περιπτώσεις: 1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`. 2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`. Απάντηση: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`. Παράδειγμα. Λύστε την εξίσωση: `sin x+cos x=1`. Λύση. Ας μετακινήσουμε όλους τους όρους της ισότητας προς τα αριστερά: `sin x+cos x-1=0`. Χρησιμοποιώντας , μετασχηματίζουμε και παραγοντοποιούμε την αριστερή πλευρά: `sin x — 2sin^2 x/2=0`, `2sin x/2 cos x/2-2sin^2 x/2=0`, `2sin x/2 (cos x/2-sin x/2)=0`, Απάντηση: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`. Αρχικά, πρέπει να μειώσετε αυτήν την τριγωνομετρική εξίσωση σε μία από τις δύο μορφές: `a sin x+b cos x=0` (ομογενής εξίσωση πρώτου βαθμού) ή `a sin^2 x + b sin x cos x +c cos^2 x=0` (ομογενής εξίσωση δεύτερου βαθμού). Στη συνέχεια, διαιρέστε και τα δύο μέρη με «cos x \ne 0» - για την πρώτη περίπτωση, και με «cos^2 x \ne 0» - για τη δεύτερη. Λαμβάνουμε εξισώσεις για «tg x»: «a tg x+b=0» και «a tg^2 x + b tg x +c =0», οι οποίες πρέπει να λυθούν χρησιμοποιώντας γνωστές μεθόδους. Παράδειγμα. Λύστε την εξίσωση: `2 sin^2 x+sin x cos x - cos^2 x=1`. Λύση. Ας γράψουμε τη δεξιά πλευρά ως `1=sin^2 x+cos^2 x`: `2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`, `2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0` `sin^2 x+sin x cos x — 2 cos^2 x=0`. Αυτή είναι μια ομοιογενής τριγωνομετρική εξίσωση του δεύτερου βαθμού, διαιρούμε την αριστερή και τη δεξιά πλευρά της με το 'cos^2 x \ne 0', παίρνουμε: `\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0` `tg^2 x+tg x — 2=0`. Ας εισάγουμε την αντικατάσταση `tg x=t`, με αποτέλεσμα `t^2 + t - 2=0`. Οι ρίζες αυτής της εξίσωσης είναι «t_1=-2» και «t_2=1». Επειτα: Απάντηση. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`. Παράδειγμα. Λύστε την εξίσωση: `11 sin x - 2 cos x = 10`. Λύση. Ας εφαρμόσουμε τους τύπους διπλής γωνίας, με αποτέλεσμα: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 συν^2 x/2` `4 tg^2 x/2 — 11 tg x/2 +6=0` Εφαρμόζοντας την αλγεβρική μέθοδο που περιγράφεται παραπάνω, λαμβάνουμε: Απάντηση. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`. Στην τριγωνομετρική εξίσωση «a sin x + b cos x =c», όπου a,b,c είναι συντελεστές και x είναι μια μεταβλητή, διαιρέστε και τις δύο πλευρές με το «sqrt (a^2+b^2)»: `\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 ) +b^2))». Οι συντελεστές στην αριστερή πλευρά έχουν τις ιδιότητες του ημιτόνου και του συνημιτόνου, δηλαδή το άθροισμα των τετραγώνων τους είναι ίσο με 1 και οι μονάδες τους δεν είναι μεγαλύτερες από 1. Ας τους συμβολίσουμε ως εξής: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, τότε: `cos \varphi sin x + sin \varphi cos x =C`. Ας ρίξουμε μια πιο προσεκτική ματιά στο ακόλουθο παράδειγμα: Παράδειγμα. Λύστε την εξίσωση: `3 sin x+4 cos x=2`. Λύση. Διαιρέστε και τις δύο πλευρές της ισότητας με το `sqrt (3^2+4^2)`, παίρνουμε: `\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))». `3/5 αμαρτία x+4/5 cos x=2/5`. Ας συμβολίσουμε `3/5 = cos \varphi` , `4/5=sin \varphi`. Εφόσον `sin \varphi>0`, `cos \varphi>0`, τότε λαμβάνουμε το `\varphi=arcsin 4/5` ως βοηθητική γωνία. Στη συνέχεια γράφουμε την ισότητά μας με τη μορφή: `cos \varphi sin x+sin \varphi cos x=2/5` Εφαρμόζοντας τον τύπο για το άθροισμα των γωνιών για το ημίτονο, γράφουμε την ισότητα μας με την ακόλουθη μορφή: `sin (x+\varphi)=2/5`, `x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`, `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`. Απάντηση. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`. Πρόκειται για ισότητες με κλάσματα των οποίων οι αριθμητές και οι παρονομαστές περιέχουν τριγωνομετρικές συναρτήσεις. Παράδειγμα. Λύστε την εξίσωση. `\frac (sin x)(1+cos x)=1-cos x`. Λύση. Πολλαπλασιάστε και διαιρέστε τη δεξιά πλευρά της ισότητας με το «(1+cos x)». Ως αποτέλεσμα παίρνουμε: `\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)` `\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)` `\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)` `\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0` `\frac (sin x-sin^2 x)(1+cos x)=0` Λαμβάνοντας υπόψη ότι ο παρονομαστής δεν μπορεί να είναι ίσος με μηδέν, παίρνουμε «1+cos x \ne 0», «cos x \ne -1», «x \ne \pi+2\pi n, n \in Z». Ας εξισώσουμε τον αριθμητή του κλάσματος με μηδέν: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Στη συνέχεια `sin x=0` ή `1-sin x=0`. Δεδομένου ότι ` x \ne \pi+2\pi n, n \in Z`, οι λύσεις είναι `x=2\pi n, n \in Z` και `x=\pi /2+2\pi n` , `n \σε Z`. Απάντηση. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`. Η τριγωνομετρία, και ειδικότερα οι τριγωνομετρικές εξισώσεις, χρησιμοποιούνται σχεδόν σε όλους τους τομείς της γεωμετρίας, της φυσικής και της μηχανικής. Η φοίτηση ξεκινά στη 10η τάξη, υπάρχουν πάντα εργασίες για την Ενιαία Κρατική Εξέταση, οπότε προσπαθήστε να θυμάστε όλους τους τύπους των τριγωνομετρικών εξισώσεων - σίγουρα θα σας φανούν χρήσιμες! Ωστόσο, δεν χρειάζεται καν να τα απομνημονεύσετε, το κύριο πράγμα είναι να κατανοήσετε την ουσία και να μπορέσετε να την αντλήσετε. Δεν είναι τόσο δύσκολο όσο φαίνεται. Δείτε μόνοι σας βλέποντας το βίντεο. Σκοπός του μαθήματος: ΕΝΑ) ενισχύουν την ικανότητα επίλυσης απλών τριγωνομετρικών εξισώσεων; σι) διδάξτε πώς να επιλέγετε ρίζες τριγωνομετρικών εξισώσεων από ένα δεδομένο διάστημα α) Έλεγχος της εργασίας: δίνεται στην τάξη προχωρημένη εργασία - λύστε μια εξίσωση και βρείτε έναν τρόπο να επιλέξετε ρίζες από ένα δεδομένο διάστημα. 1) συν Χ= -0,5, όπου xI [- ]. Απάντηση:. 2) αμαρτία Χ= , όπου xI . Απάντηση: ; . 3) συν 2 Χ= -, όπου xI. Απάντηση: Οι μαθητές καταγράφουν τη λύση στον πίνακα, άλλοι χρησιμοποιώντας γράφημα, άλλοι χρησιμοποιώντας τη μέθοδο επιλογής. Αυτή την ώρα μάθημα λειτουργεί προφορικά. Βρείτε το νόημα της έκφρασης: α) tg – αμαρτία + συν + αμαρτία. Απάντηση: 1. β) 2 τόξο 0 + 3 τόξο 1. Απάντηση: ? γ) arcsin + arcsin. Απάντηση:. δ) 5 arctg (-) – arccos (-). Απάντηση:-. – Ας ελέγξουμε την εργασία σας, ανοίξτε τα τετράδιά σας με τις εργασίες για το σπίτι. Κάποιοι από εσάς βρήκαν τη λύση χρησιμοποιώντας τη μέθοδο επιλογής και άλλοι χρησιμοποιώντας το γράφημα. 2. Συμπέρασμα σχετικά με τρόπους επίλυσης αυτών των εργασιών και δήλωση του προβλήματος, δηλ. επικοινωνία του θέματος και του σκοπού του μαθήματος. – α) Είναι δύσκολο να λυθεί με τη χρήση επιλογής εάν δοθεί μεγάλο διάστημα. – β) Η γραφική μέθοδος δεν δίνει ακριβή αποτελέσματα, απαιτεί επαλήθευση και απαιτεί πολύ χρόνο. – Επομένως, πρέπει να υπάρχει τουλάχιστον μια ακόμη μέθοδος, η πιο καθολική - ας προσπαθήσουμε να τη βρούμε. Λοιπόν, τι θα κάνουμε σήμερα στην τάξη; (Μάθετε να επιλέγετε τις ρίζες μιας τριγωνομετρικής εξίσωσης σε ένα δεδομένο διάστημα.) – Παράδειγμα 1. (Ο μαθητής πηγαίνει στον πίνακα) cos Χ= -0,5, όπου xI [- ]. Ερώτηση: Τι καθορίζει την απάντηση σε αυτήν την εργασία; (Από τη γενική λύση της εξίσωσης. Ας γράψουμε τη λύση σε γενική μορφή). Η λύση είναι γραμμένη στον πίνακα x = + 2?k, όπου k R. – Ας γράψουμε αυτή τη λύση με τη μορφή συνόλου: – Κατά τη γνώμη σας, σε ποια σημειογραφία της λύσης είναι βολικό να επιλέξετε ρίζες στο διάστημα; (από το δεύτερο λήμμα). Αλλά αυτή είναι και πάλι μια μέθοδος επιλογής. Τι πρέπει να γνωρίζουμε για να λάβουμε τη σωστή απάντηση; (Πρέπει να γνωρίζετε τις τιμές του k). (Ας δημιουργήσουμε ένα μαθηματικό μοντέλο για να βρούμε το k). αφού kI Z, τότε k = 0, επομένως Χ= = Από αυτή την ανισότητα είναι σαφές ότι δεν υπάρχουν ακέραιες τιμές του k. Συμπέρασμα:Για να επιλέξετε ρίζες από ένα δεδομένο διάστημα κατά την επίλυση μιας τριγωνομετρικής εξίσωσης, πρέπει: Λύστε τα παραδείγματα Νο. 2 και Νο. 3 από την εργασία στο σπίτι χρησιμοποιώντας τον αλγόριθμο που προκύπτει. Δύο μαθητές εργάζονται στον πίνακα ταυτόχρονα και ακολουθεί έλεγχος της εργασίας.Απάντηση
Κατάσταση
Λύση

Απάντηση
Κατάσταση
δεν περιλαμβάνεται στο DZ. Απάντηση
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα [-7Pi/2; -2 Pi]
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
-15/8 μικρότερο ή ίσο με n μικρότερο ή ίσο με -9/8
-13/8 μικρότερο ή ίσο με n μικρότερο ή ίσο με -7/8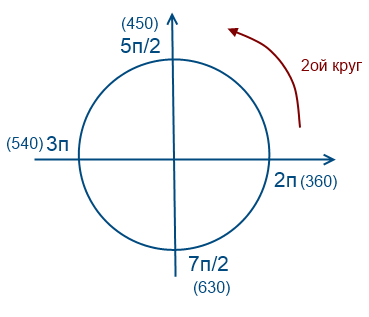


Η λύση του προβλήματος





Τύποι για τις ρίζες των τριγωνομετρικών εξισώσεων στον πίνακα
 Για το συνημίτονο:
Για το συνημίτονο:  Για εφαπτομένη και συνεφαπτομένη:
Για εφαπτομένη και συνεφαπτομένη:  Τύποι επίλυσης εξισώσεων που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις:
Τύποι επίλυσης εξισώσεων που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις:
Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων
Αλγεβρική μέθοδος.
Παραγοντοποίηση.
Αναγωγή σε ομοιογενή εξίσωση
Μετακίνηση στη μισή γωνία
Εισαγωγή βοηθητικής γωνίας
Κλασματικές ορθολογικές τριγωνομετρικές εξισώσεις
Κατά τη διάρκεια των μαθημάτων.
1. Επικαιροποίηση γνώσεων.

3. Ενοποίηση.








