Αρχή της ελάχιστης δράσης. Αρχή ελάχιστης δράσης Αρχή ελάχιστης δράσης στη φυσική

Όταν ήμουν στο σχολείο, ο καθηγητής φυσικής μας, ονόματι Bader, με κάλεσε κάποτε μετά το μάθημα και μου είπε: «Φαίνεσαι σαν να είσαι τρομερά κουρασμένος από τα πάντα. ακούστε ένα ενδιαφέρον πράγμα». Και μου είπε κάτι που νόμιζα ότι ήταν πραγματικά συναρπαστικό. Ακόμα και τώρα, αν και έχει περάσει πολύς καιρός από τότε, συνεχίζει να με συναρπάζει. Και κάθε φορά που θυμάμαι τι είπα, επιστρέφω στη δουλειά. Και αυτή τη φορά, ενώ προετοιμαζόμουν για τη διάλεξη, βρέθηκα να αναλύω ξανά τα ίδια πράγματα. Και, αντί να προετοιμαστώ για τη διάλεξη, ανέλαβα ένα νέο πρόβλημα. Το θέμα για το οποίο μιλάω είναι αρχή της ελάχιστης δράσης.

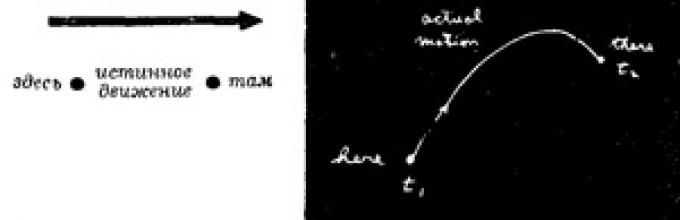
«Αυτό μου είπε τότε ο δάσκαλός μου Bader: «Ας, για παράδειγμα, έχετε ένα σωματίδιο στο βαρυτικό πεδίο. αυτό το σωματίδιο, έχοντας βγει από κάπου, κινείται ελεύθερα κάπου αλλού σε άλλο σημείο. Το πέταξες, ας πούμε, επάνω, και πέταξε και μετά έπεσε.

Της πήρε λίγο χρόνο για να ταξιδέψει από την αφετηρία στην τελική θέση. Τώρα δοκιμάστε κάποια άλλη κίνηση. Αφήστε την να μετακινηθεί «από εδώ ως εδώ» όχι πια όπως πριν, αλλά ως εξής:

Αλλά παρόλα αυτά βρέθηκα στο σωστό μέρος την ίδια χρονική στιγμή όπως πριν».

«Και έτσι», συνέχισε ο δάσκαλος, «αν υπολογίσετε την κινητική ενέργεια σε κάθε χρονική στιγμή κατά μήκος της διαδρομής του σωματιδίου, αφαιρέσετε τη δυναμική ενέργεια από αυτήν και ενσωματώσετε τη διαφορά σε όλο το χρόνο που έγινε η κίνηση, θα δείτε ότι ο αριθμός που θα πάρετε θα είναι περισσότερο,παρά για αληθινή κίνηση σωματιδίων.

Με άλλα λόγια, οι νόμοι του Νεύτωνα μπορούν να διατυπωθούν όχι ως F=ma, αλλά ως εξής: η μέση κινητική ενέργεια μείον τη μέση δυναμική ενέργεια φτάνει στη χαμηλότερη τιμή της κατά μήκος της τροχιάς κατά την οποία ένα αντικείμενο κινείται πραγματικά από το ένα μέρος στο άλλο.

Θα προσπαθήσω να σας το εξηγήσω λίγο πιο ξεκάθαρα.
Αν πάρουμε το βαρυτικό πεδίο και ορίσουμε την τροχιά του σωματιδίου Χ(t), Οπου Χ- ύψος πάνω από το έδαφος (ας περάσουμε με μια διάσταση προς το παρόν, αφήστε την τροχιά να τρέχει μόνο πάνω-κάτω, και όχι στα πλάγια), τότε η κινητική ενέργεια θα είναι y 2 Μ(dx/ dt) 2, αη δυναμική ενέργεια σε μια αυθαίρετη χρονική στιγμή θα είναι ίση με mgx.

Τώρα, για κάποια στιγμή κίνησης κατά μήκος της τροχιάς, παίρνω τη διαφορά μεταξύ της κινητικής και της δυνητικής ενέργειας και ενσωματώνω καθ' όλη τη διάρκεια του χρόνου από την αρχή μέχρι το τέλος. Αφήστε την αρχική στιγμή t x η κίνηση άρχισε σε κάποιο ύψος και τελείωσε τη στιγμή t 2 σε άλλο ορισμένο ύψος.

Τότε το ολοκλήρωμα είναι ίσο με ∫ t2 t1 dt

Η αληθινή κίνηση εμφανίζεται κατά μήκος μιας ορισμένης καμπύλης (σε συνάρτηση με το χρόνο είναι παραβολή) και οδηγεί σε μια ορισμένη ακέραια τιμή. Αλλά μπορείς πρινβάζωφανταστείτε κάποια άλλη κίνηση: πρώτα μια απότομη άνοδο και μετά μερικές παράξενες διακυμάνσεις.

Μπορείτε να υπολογίσετε τη διαφορά μεταξύ δυναμικής και κινητικής ενέργειας σε αυτό το μονοπάτι... ή σε οποιοδήποτε άλλο. Και το πιο εκπληκτικό είναι ότι η πραγματική διαδρομή είναι αυτή κατά μήκος της οποίας αυτό το ολοκλήρωμα είναι το μικρότερο.
Ας το ελέγξουμε. Αρχικά, ας δούμε αυτήν την περίπτωση: ένα ελεύθερο σωματίδιο δεν έχει καθόλου δυναμική ενέργεια. Τότε ο κανόνας λέει ότι όταν μετακινούμαστε από ένα σημείο σε ένα άλλο σε δεδομένο χρόνο, το ολοκλήρωμα της κινητικής ενέργειας πρέπει να είναι το μικρότερο. Αυτό σημαίνει ότι το σωματίδιο πρέπει να κινείται ομοιόμορφα. (Και αυτό είναι σωστό, εσείς και εγώ γνωρίζουμε ότι η ταχύτητα σε μια τέτοια κίνηση είναι σταθερή.) Γιατί ομοιόμορφα; Ας το καταλάβουμε. Εάν ήταν διαφορετικά, τότε η ταχύτητα του σωματιδίου θα ξεπερνούσε κατά καιρούς τον μέσο όρο, και μερικές φορές θα ήταν κάτω από αυτόν, και η μέση ταχύτητα θα ήταν η ίδια, επειδή το σωματίδιο θα έπρεπε να φτάσει «από εδώ ως εδώ» στο τον συμφωνημένο χρόνο. Για παράδειγμα, εάν πρέπει να πάτε από το σπίτι στο σχολείο με το αυτοκίνητό σας σε μια συγκεκριμένη ώρα, τότε μπορείτε να το κάνετε αυτό με διαφορετικούς τρόπους: μπορείτε να οδηγείτε σαν τρελοί στην αρχή και να επιβραδύνετε στο τέλος ή να οδηγείτε με την ίδια ταχύτητα, ή μπορείτε ακόμη και να πάτε στην αντίθετη πλευρά και μόνο τότε να στρίψετε προς το σχολείο κ.λπ. Σε όλες τις περιπτώσεις, η μέση ταχύτητα, φυσικά, θα πρέπει να είναι η ίδια - το πηλίκο της απόστασης από το σπίτι στο σχολείο διαιρούμενο με το χρόνο. Αλλά ακόμα και με αυτή τη μέση ταχύτητα, μερικές φορές κινήσατε πολύ γρήγορα και μερικές φορές πολύ αργά. Και μέτριο τετράγωνοκάτι που αποκλίνει από τον μέσο όρο είναι, όπως γνωρίζουμε, πάντα μεγαλύτερο από το τετράγωνο του μέσου όρου. Αυτό σημαίνει ότι το ολοκλήρωμα της κινητικής ενέργειας κατά τις διακυμάνσεις της ταχύτητας κίνησης θα είναι πάντα μεγαλύτερο από όταν κινείται με σταθερή ταχύτητα. Βλέπετε ότι το ολοκλήρωμα θα φτάσει στο ελάχιστο όταν η ταχύτητα είναι σταθερή (ελλείψει δυνάμεων). Ο σωστός τρόπος είναι αυτός.

Ένα αντικείμενο που ρίχνεται προς τα πάνω σε ένα πεδίο βαρύτητας ανεβαίνει γρήγορα στην αρχή και μετά όλο και πιο αργά. Αυτό συμβαίνει επειδή έχει επίσης δυναμική ενέργεια και η ελάχιστη τιμή του θα πρέπει να φτάσει μια φοράnessμεταξύ κινητικής και δυνητικής ενέργειας.. Εφόσον η δυναμική ενέργεια αυξάνεται καθώς ανεβαίνετε, τότε λιγότερη διαφοράΘα λειτουργήσει εάν φτάσετε εκείνα τα ύψη όπου η δυνητική ενέργεια είναι υψηλή όσο το δυνατόν γρηγορότερα. Στη συνέχεια, αφαιρώντας αυτό το υψηλό δυναμικό από την κινητική ενέργεια, επιτυγχάνουμε μείωση του μέσου όρου. Άρα το μονοπάτι που ανεβαίνει και τροφοδοτεί ένα καλό αρνητικό κομμάτι σε βάρος της δυνητικής ενέργειας είναι πιο κερδοφόρο.

Αυτό μου είπε ο δάσκαλός μου, γιατί ήταν πολύ καλός δάσκαλος και ήξερε πότε ήταν η ώρα να σταματήσει. Εγώ ο ίδιος, δυστυχώς, δεν είμαι έτσι. Μου είναι δύσκολο να σταματήσω στην ώρα μου. Και έτσι, αντί να σας προκαλέσω απλώς το ενδιαφέρον με την ιστορία μου, θέλω να σας εκφοβίσω, θέλω να σας αρρωστήσω με την πολυπλοκότητα της ζωής - θα προσπαθήσω να αποδείξω αυτό που σας είπα. Το μαθηματικό πρόβλημα που θα λύσουμε είναι πολύ δύσκολο και μοναδικό. Υπάρχει μια συγκεκριμένη ποσότητα μικρό, που ονομάζεται δράση.Είναι ίσο με την κινητική ενέργεια μείον τη δυναμική ενέργεια που ενσωματώνεται με την πάροδο του χρόνου:

Αλλά από την άλλη, δεν μπορείτε να κινηθείτε πολύ γρήγορα ή να πάτε πολύ ψηλά, γιατί αυτό θα απαιτούσε υπερβολική κινητική ενέργεια. Πρέπει να κινηθείτε αρκετά γρήγορα για να ανεβοκατεβείτε μέσα στον δεδομένο χρόνο που έχετε στη διάθεσή σας. Επομένως, δεν πρέπει να προσπαθήσετε να πετάξετε πολύ ψηλά, αλλά απλώς να φτάσετε σε κάποιο λογικό επίπεδο. Ως αποτέλεσμα, αποδεικνύεται ότι η λύση είναι ένα είδος ισορροπίας μεταξύ της επιθυμίας για απόκτηση όσο το δυνατόν περισσότερης δυναμικής ενέργειας και της επιθυμίας να μειωθεί όσο το δυνατόν περισσότερο η ποσότητα της κινητικής ενέργειας - αυτή είναι η επιθυμία να επιτευχθεί μέγιστη μείωση στη διαφορά μεταξύ κινητικής και δυνητικής ενέργειας».

Μην ξεχνάτε ότι η π.ε. και κ.ε.—και οι δύο συναρτήσεις του χρόνου. Για κάθε νέο νοητό μονοπάτι, αυτή η ενέργεια αποκτά το συγκεκριμένο νόημά της. Το μαθηματικό πρόβλημα είναι να προσδιοριστεί ποια καμπύλη έχει αυτόν τον αριθμό μικρότερο από τις άλλες.

Λέτε, «Ω, αυτό είναι απλώς ένα απλό παράδειγμα μέγιστου και ελαχίστου. Πρέπει να υπολογίσουμε τη δράση, να τη διαφοροποιήσουμε και να βρούμε το ελάχιστο».

Αλλά περίμενε. Συνήθως έχουμε μια συνάρτηση κάποιας μεταβλητής και πρέπει να βρούμε την τιμή μεταβλητός,στην οποία η συνάρτηση γίνεται μικρότερη ή μεγαλύτερη. Ας πούμε ότι υπάρχει μια ράβδος που θερμαίνεται στη μέση. Η θερμότητα απλώνεται πάνω του και η δική της θερμοκρασία εδραιώνεται σε κάθε σημείο της ράβδου. Πρέπει να βρείτε το σημείο όπου είναι υψηλότερο. Αλλά μιλάμε για κάτι εντελώς διαφορετικό - κάθε μονοπάτι στο διάστημααπαντά στον αριθμό του και υποτίθεται ότι θα βρει αυτόν μονοπάτι,για την οποία ο αριθμός αυτός είναι ελάχιστος. Αυτός είναι ένας εντελώς διαφορετικός τομέας των μαθηματικών. Αυτό δεν είναι συνηθισμένος λογισμός, αλλά μεταβλητή(έτσι τον λένε).

Αυτός ο τομέας των μαθηματικών έχει πολλά από τα δικά του προβλήματα. Ας πούμε, ένας κύκλος ορίζεται συνήθως ως ο τόπος των σημείων των οποίων οι αποστάσεις από ένα δεδομένο σημείο είναι ίδιες, αλλά ένας κύκλος μπορεί να οριστεί διαφορετικά: είναι μια από τις καμπύλες δεδομένου μήκους,που περικλείει τη μεγαλύτερη έκταση. Οποιαδήποτε άλλη καμπύλη της ίδιας περιμέτρου περικλείει μια περιοχή μικρότερη από τον κύκλο. Αν λοιπόν ορίσουμε το καθήκον: να βρούμε την καμπύλη μιας δεδομένης περιμέτρου που οριοθετεί τη μεγαλύτερη περιοχή, τότε θα έχουμε πρόβλημα από τον λογισμό των διακυμάνσεων και όχι από τον λογισμό στον οποίο είστε συνηθισμένοι.

Έτσι, θέλουμε να πάρουμε το ολοκλήρωμα πάνω από το μονοπάτι που διανύει το σώμα. Ας το κάνουμε με αυτόν τον τρόπο. Το όλο θέμα είναι να φανταστούμε ότι υπάρχει μια αληθινή διαδρομή και ότι οποιαδήποτε άλλη καμπύλη που σχεδιάζουμε δεν είναι η πραγματική διαδρομή, έτσι ώστε αν υπολογίσουμε την ενέργεια για αυτήν, θα πάρουμε έναν αριθμό μεγαλύτερο από αυτό που παίρνουμε για την αντίστοιχη ενέργεια στον πραγματικό τρόπο.

Οπότε, το καθήκον είναι να βρούμε το αληθινό μονοπάτι. Πού βρίσκεται; Ένας τρόπος, φυσικά, θα ήταν να μετρήσετε τη δράση για εκατομμύρια και εκατομμύρια μονοπάτια και μετά να δείτε ποια διαδρομή έχει τη μικρότερη ενέργεια. Αυτή είναι η διαδρομή στην οποία η δράση είναι ελάχιστη και θα είναι πραγματική.

Αυτή η μέθοδος είναι αρκετά δυνατή. Ωστόσο, μπορεί να γίνει πιο απλά. Εάν υπάρχει μια ποσότητα που έχει ένα ελάχιστο (από συνηθισμένες συναρτήσεις, ας πούμε, θερμοκρασία), τότε μια από τις ιδιότητες του ελάχιστου είναι ότι όταν απομακρύνεστε από αυτήν σε απόσταση πρώτατάξης μικρότητας, η συνάρτηση αποκλίνει από την ελάχιστη τιμή της μόνο κατά το ποσό δεύτεροςΣειρά. Και σε οποιοδήποτε άλλο σημείο της καμπύλης, μια μετατόπιση κατά μια μικρή απόσταση αλλάζει την τιμή της συνάρτησης επίσης κατά μια τιμή της πρώτης τάξης μικρότητας. Αλλά τουλάχιστον, μικρές αποκλίσεις στο πλάι δεν οδηγούν σε αλλαγή της λειτουργίας ως πρώτη προσέγγιση.

Αυτή είναι η ιδιότητα που πρόκειται να χρησιμοποιήσουμε για να υπολογίσουμε την πραγματική διαδρομή.

Εάν η διαδρομή είναι σωστή, τότε μια καμπύλη ελαφρώς διαφορετική από αυτήν δεν θα οδηγήσει, ως πρώτη προσέγγιση, σε αλλαγή του μεγέθους της δράσης. Όλες οι αλλαγές, εάν αυτό ήταν πραγματικά το ελάχιστο, θα εμφανιστούν μόνο στη δεύτερη προσέγγιση.

Αυτό είναι εύκολο να αποδειχθεί. Εάν, με κάποια απόκλιση από την καμπύλη, πραγματοποιηθούν αλλαγές στην πρώτη σειρά, τότε αυτές οι αλλαγές ισχύουν αναλογικάαπόκλιση. Είναι πιθανό να αυξήσουν το αποτέλεσμα. αλλιώς δεν θα ήταν ελάχιστο. Μόλις όμως οι αλλαγές αναλογικάαπόκλιση, τότε η αλλαγή του πρόσημου της απόκλισης θα μειώσει το αποτέλεσμα. Αποδεικνύεται ότι όταν παρεκκλίνετε προς μία κατεύθυνση, το αποτέλεσμα αυξάνεται και όταν αποκλίνετε προς την αντίθετη κατεύθυνση, μειώνεται. Η μόνη πιθανότητα να είναι πραγματικά ένα ελάχιστο είναι ότι, ως πρώτη προσέγγιση, δεν συμβαίνουν αλλαγές και οι αλλαγές είναι ανάλογες με το τετράγωνο της απόκλισης από την πραγματική διαδρομή.

Άρα, θα ακολουθήσουμε την ακόλουθη διαδρομή: συμβολίζουμε με Χ(t) (με μια γραμμή παρακάτω) το αληθινό μονοπάτι είναι αυτό που θέλουμε να βρούμε. Ας κάνουμε μια δοκιμαστική πορεία Χ(t), διαφέρει από το επιθυμητό κατά μια μικρή ποσότητα, την οποία συμβολίζουμε η (t).

Η ιδέα είναι ότι αν μετρήσουμε τη δράση μικρό σε έναν τρόπο Χ(t), τότε η διαφορά μεταξύ αυτού μικρό και με την ενέργεια που υπολογίσαμε για τη διαδρομή Χ(t) (για απλότητα θα οριστεί μικρό), ή η διαφορά μεταξύ μικρό_ Και μικρό, πρέπει να είναι μια πρώτη προσέγγιση η μηδέν. Μπορεί να διαφέρουν στη δεύτερη σειρά, αλλά στην πρώτη η διαφορά πρέπει να είναι μηδέν.

Και αυτό πρέπει να τηρείται για όλους η . Ωστόσο, όχι για όλους. Η μέθοδος απαιτεί να λαμβάνονται υπόψη μόνο εκείνα τα μονοπάτια που όλα ξεκινούν και τελειώνουν στο ίδιο ζεύγος σημείων, δηλαδή, κάθε διαδρομή πρέπει να ξεκινά σε ένα συγκεκριμένο σημείο τη στιγμή t 1 και τελειώνει σε άλλο συγκεκριμένο σημείο αυτή τη στιγμή t 2 . Αυτά τα σημεία και οι στιγμές καταγράφονται. Άρα η συνάρτησή μας δ) (απόκλιση) πρέπει να είναι μηδέν και στα δύο άκρα: η (t 1 )= 0 Και η (t 2)=0. Υπό αυτή την προϋπόθεση, το μαθηματικό μας πρόβλημα καθίσταται πλήρως καθορισμένο.

Αν δεν ήξερες τον λογισμό, θα μπορούσες να κάνεις το ίδιο πράγμα για να βρεις το ελάχιστο μιας συνηθισμένης συνάρτησης φά(Χ). Θα σκεφτόσασταν τι θα γινόταν αν έπαιρνα φά(Χ) και προσθέστε σε Χμικρή ποσότητα η, και θα υποστήριζε ότι η τροπολογία σε φά(Χ) σε πρώτη σειρά η πρέπει να είναι τουλάχιστον ίσο με μηδέν. Θα με ρυθμίσεις x+η αντί Χκαι θα επέκτεινε το j(x+h) μέχρι την πρώτη δύναμη η. . ., με μια λέξη, θα επαναλάμβανε όλα όσα σκοπεύουμε να κάνουμε η .

Εάν το δούμε τώρα προσεκτικά, θα δούμε ότι οι δύο πρώτοι όροι που γράφτηκαν εδώ αντιστοιχούν σε αυτήν την ενέργεια μικρό, που θα έγραφα για το αναζητούμενο αληθινό μονοπάτι Χ.Θέλω να εστιάσω την προσοχή σας στην αλλαγή. μικρό, δηλαδή στη διαφορά μεταξύ μικρό και έτσι μικρό_, που θα προέκυπτε για το αληθινό μονοπάτι. Θα γράψουμε αυτή τη διαφορά ως bS και ας το πούμε παραλλαγή μικρό. Απορρίπτοντας τις «δεύτερες και ανώτερες παραγγελίες», λαμβάνουμε για σS

Τώρα η εργασία μοιάζει με αυτό. Εδώ μπροστά μου είναι μερικά αναπόσπαστα. Δεν ξέρω ακόμα πώς είναι, αλλά ξέρω σίγουρα ότι, τι η Ό,τι κι αν γίνει, αυτό το ολοκλήρωμα πρέπει να είναι ίσο με μηδέν. «Λοιπόν», μπορεί να σκεφτείτε, «ο μόνος τρόπος για να συμβεί αυτό είναι να το κάνει ο πολλαπλασιαστής η ήταν ίσο με μηδέν». Τι γίνεται όμως με την πρώτη θητεία, όπου υπάρχει ρε η / dt? Λέτε: «Αν η μετατρέπεται σε τίποτα, τότε το παράγωγό του είναι το ίδιο τίποτα. αυτό σημαίνει ο συντελεστής στο dv\/ dt πρέπει επίσης να είναι μηδέν». Λοιπόν, αυτό δεν είναι απολύτως αλήθεια. Αυτό δεν είναι απολύτως αληθές γιατί μεταξύ της απόκλισης η και το παράγωγο του υπάρχει σύνδεση? δεν είναι εντελώς ανεξάρτητοι γιατί η (t) πρέπει να είναι μηδέν και t 1 και στο t 2 .

Κατά την επίλυση όλων των προβλημάτων του λογισμού των μεταβολών, χρησιμοποιείται πάντα η ίδια γενική αρχή. Αλλάζετε ελαφρώς αυτό που θέλετε να διαφοροποιήσετε (παρόμοιο με αυτό που κάναμε προσθέτοντας η ), μια ματιά στους όρους πρώτης τάξης, έπειτατακτοποιήστε τα πάντα έτσι ώστε να έχετε ένα ολοκλήρωμα στην ακόλουθη μορφή: «βάρδια (η ), πολλαπλασιάζεται με αυτό που προκύπτει», αλλά έτσι ώστε να μην περιέχει παράγωγα του η (όχι ρε η / dt). Είναι απολύτως απαραίτητο να μεταμορφωθούν τα πάντα έτσι ώστε «κάτι» να παραμείνει, πολλαπλασιασμένο επί η . Τώρα θα καταλάβετε γιατί αυτό είναι τόσο σημαντικό. (Υπάρχουν τύποι που θα σας πουν πώς σε ορισμένες περιπτώσεις μπορείτε να το κάνετε αυτό χωρίς υπολογισμούς, αλλά δεν είναι τόσο γενικοί ώστε να αξίζει να απομνημονεύσετε. Είναι καλύτερο να κάνετε τους υπολογισμούς με τον τρόπο που το κάνουμε.)

Πώς μπορώ να ξαναφτιάξω ένα πέος ρε η / dt, ώστε να φαίνεται η ? Αυτό μπορώ να το πετύχω ενσωματώνοντας κομμάτι κομμάτι. Αποδεικνύεται ότι στον λογισμό των παραλλαγών το όλο κόλπο είναι να περιγράψουμε την παραλλαγή μικρό και στη συνέχεια να ενσωματωθούν κατά μέρη έτσι ώστε οι παράγωγοι του η εξαφανίστηκε. Σε όλα τα προβλήματα στα οποία εμφανίζονται παράγωγα, γίνεται το ίδιο κόλπο.

Θυμηθείτε τη γενική αρχή της ολοκλήρωσης ανά εξαρτήματα. Εάν έχετε μια αυθαίρετη συνάρτηση f πολλαπλασιαζόμενη επί ρε η / dt και ενσωματώνεται με t, τότε γράφεις την παράγωγο του η /t

Τα όρια της ολοκλήρωσης πρέπει να αντικατασταθούν στον πρώτο όρο t 1 Και t 2 . Στη συνέχεια, κάτω από το ολοκλήρωμα θα λάβω τον όρο από την ολοκλήρωση κατά μέρη και τον τελευταίο όρο που παραμένει αμετάβλητος κατά τη διάρκεια του μετασχηματισμού.
Και τώρα συμβαίνει αυτό που συμβαίνει πάντα - το ολοκληρωμένο μέρος εξαφανίζεται. (Και αν δεν εξαφανιστεί, τότε η αρχή πρέπει να αναδιατυπωθεί, προσθέτοντας συνθήκες που εξασφαλίζουν μια τέτοια εξαφάνιση!) Έχουμε ήδη πει ότι η στα άκρα της διαδρομής πρέπει να είναι ίσο με μηδέν. Τελικά ποια είναι η αρχή μας; Γεγονός είναι ότι η δράση είναι ελάχιστη με την προϋπόθεση ότι η μεταβλητή καμπύλη αρχίζει και τελειώνει σε επιλεγμένα σημεία. Αυτό σημαίνει ότι η (t 1)=0 και η (t 2)=0. Επομένως, ο ολοκληρωμένος όρος αποδεικνύεται μηδέν. Μαζεύουμε τα υπόλοιπα μέλη και γράφουμε

Παραλλαγή μικρό έχει πλέον αποκτήσει τη μορφή που θέλαμε να του δώσουμε: κάτι είναι μέσα σε αγκύλες (ας το υποδηλώσουμε φά), και όλα αυτά πολλαπλασιάζονται επί η (t) και ενσωματωμένο από t t πριν t 2 .
Αποδείχθηκε ότι το ολοκλήρωμα κάποιας έκφρασης πολλαπλασιάζεται επί η (t), πάντα ίσο με μηδέν:

Υπάρχει κάποια λειτουργία από t; το πολλαπλασιάζω επί η (t) και ενσωματώστε το από την αρχή μέχρι το τέλος. Και ό,τι κι αν είναι η, παίρνω μηδέν. Αυτό σημαίνει ότι η συνάρτηση φά(t) ίσο με μηδέν. Σε γενικές γραμμές, αυτό είναι προφανές, αλλά για κάθε περίπτωση, θα σας δείξω έναν τρόπο για να το αποδείξετε.

Έστω ως η (t) Θα επιλέξω κάτι που ισούται με το μηδέν παντού, για όλους t, εκτός από μία προεπιλεγμένη τιμή t. Παραμένει μηδέν μέχρι να φτάσω εκεί t, sΜετά πηδά για μια στιγμή και αμέσως πέφτει πίσω. Αν πάρετε το ολοκλήρωμα αυτού του m) πολλαπλασιασμένο με κάποια συνάρτηση φά, το μόνο μέρος που θα πάρετε κάτι μη μηδενικό είναι που η (t) πήδηξε επάνω? και θα πάρεις την αξία φά σε αυτό το σημείο στο ολοκλήρωμα πάνω από το άλμα. Το ολοκλήρωμα πάνω από το ίδιο το άλμα δεν είναι ίσο με μηδέν, αλλά μετά τον πολλαπλασιασμό με φά θα πρέπει να δίνει μηδέν. Αυτό σημαίνει ότι η συνάρτηση στο σημείο όπου έγινε άλμα πρέπει να αποδειχθεί μηδενική. Αλλά το άλμα θα μπορούσε να είχε γίνει οπουδήποτε. Που σημαίνει, φά πρέπει να είναι μηδέν παντού.

Βλέπουμε ότι αν το ολοκλήρωμα μας είναι ίσο με μηδέν για οποιοδήποτε η , τότε ο συντελεστής στο η πρέπει να πάει στο μηδέν. Το ολοκλήρωμα δράσης φτάνει στο ελάχιστο κατά μήκος της διαδρομής που θα ικανοποιήσει μια τέτοια πολύπλοκη διαφορική εξίσωση:

Στην πραγματικότητα δεν είναι τόσο περίπλοκο. τον έχεις ξανασυναντήσει. Είναι απλώς F=ma. Ο πρώτος όρος είναι η μάζα επί της επιτάχυνσης. το δεύτερο είναι το παράγωγο της δυναμικής ενέργειας, δηλαδή η δύναμη.

Έτσι δείξαμε (τουλάχιστον για ένα συντηρητικό σύστημα) ότι η αρχή της ελάχιστης δράσης οδηγεί στη σωστή απάντηση. δηλώνει ότι το μονοπάτι που έχει την ελάχιστη δράση είναι το μονοπάτι που ικανοποιεί το νόμο του Νεύτωνα.

Πρέπει να γίνει μια ακόμη παρατήρηση. Δεν το έχω αποδείξει αυτό ελάχιστο.Ίσως αυτό είναι το μέγιστο. Στην πραγματικότητα, αυτό δεν χρειάζεται να είναι το ελάχιστο. Εδώ όλα είναι τα ίδια όπως στην "αρχή του συντομότερου χρόνου", την οποία συζητήσαμε κατά τη μελέτη της οπτικής. Και εκεί μιλήσαμε για πρώτη φορά για τον «μικρότερο» χρόνο. Ωστόσο, αποδείχθηκε ότι υπάρχουν καταστάσεις στις οποίες αυτός ο χρόνος δεν είναι απαραίτητα ο «μικρότερος». Η θεμελιώδης αρχή είναι ότι για οποιαδήποτε αποκλίσεις πρώτης τάξηςαπό την οπτική διαδρομή αλλαγέςχρονικά θα ήταν ίσο με μηδέν. Εδώ είναι η ίδια ιστορία. Με τον όρο "ελάχιστο" εννοούμε στην πραγματικότητα ότι στην πρώτη τάξη μικρότητας της μεταβολής της ποσότητας μικρόόταν οι αποκλίσεις από τη διαδρομή πρέπει να είναι ίσες με μηδέν. Και αυτό δεν είναι απαραίτητα το «ελάχιστο».

Τώρα θέλω να προχωρήσω σε κάποιες γενικεύσεις. Πρώτα από όλα, όλη αυτή η ιστορία θα μπορούσε να γίνει σε τρεις διαστάσεις. Αντί για απλό Χτότε θα είχα x, yΚαι zως λειτουργίες t,και η δράση θα φαινόταν πιο περίπλοκη. Όταν κινείστε σε 3D πρέπει να χρησιμοποιείτε πλήρη κινητική ενέργεια): (t/2),πολλαπλασιαζόμενο με το τετράγωνο της συνολικής ταχύτητας. Με άλλα λόγια

Επιπλέον, η δυναμική ενέργεια είναι πλέον συνάρτηση x, yΚαι z.Τι μπορείτε να πείτε για το μονοπάτι; Μια διαδρομή είναι μια ορισμένη γενική καμπύλη στο χώρο. δεν είναι τόσο εύκολο να σχεδιάσετε, αλλά η ιδέα παραμένει η ίδια. Τι γίνεται με το η; Λοιπόν, το η έχει επίσης τρία συστατικά. Η διαδρομή μπορεί να μετατοπιστεί τόσο σε x όσο και σε y,και από z,ή και στις τρεις κατευθύνσεις ταυτόχρονα. Έτσι η τώρα ένα διάνυσμα. Αυτό δεν δημιουργεί σημαντικές επιπλοκές. Μόνο οι παραλλαγές πρέπει να είναι ίσες με μηδέν πρώτη σειράτότε ο υπολογισμός μπορεί να πραγματοποιηθεί διαδοχικά με τρεις βάρδιες. Πρώτα μπορείτε να μετακινηθείτε tsμόνο προς την κατεύθυνση Χκαι πείτε ότι ο συντελεστής πρέπει να πάει στο μηδέν. Παίρνετε μια εξίσωση. Μετά θα κινηθούμε tsστην κατεύθυνση στοκαι παίρνουμε το δεύτερο. Στη συνέχεια, κινηθείτε προς την κατεύθυνση zκαι παίρνουμε το τρίτο. Μπορείτε να κάνετε τα πάντα, αν θέλετε, με διαφορετική σειρά. Όπως και να έχει, προκύπτει μια τριάδα εξισώσεων. Αλλά ο νόμος του Νεύτωνα είναι επίσης τρεις εξισώσεις σε τρεις διαστάσεις, μία για κάθε συστατικό. Μένεις να δεις μόνος σου ότι όλα αυτά λειτουργούν σε τρεις διαστάσεις (δεν υπάρχει πολλή δουλειά εδώ). Παρεμπιπτόντως, μπορείτε να πάρετε οποιοδήποτε σύστημα συντεταγμένων θέλετε, πολικό, οποιοδήποτε, και να αποκτήσετε αμέσως τους νόμους του Νεύτωνα σε σχέση με αυτό το σύστημα, λαμβάνοντας υπόψη τι συμβαίνει όταν συμβαίνει μια μετατόπιση η κατά μήκος μιας ακτίνας ή κατά μήκος μιας γωνίας κ.λπ.

Η μέθοδος μπορεί να γενικευτεί σε έναν αυθαίρετο αριθμό σωματιδίων. Εάν, ας πούμε, έχετε δύο σωματίδια και υπάρχουν κάποιες δυνάμεις που ενεργούν μεταξύ τους και υπάρχει αμοιβαία δυναμική ενέργεια, τότε απλά προσθέτετε τις κινητικές τους ενέργειες και αφαιρείτε τη δυναμική ενέργεια αλληλεπίδρασης από το άθροισμα. Τι διαφέρεις; Μονοπάτια και τα δυοσωματίδια. Στη συνέχεια, για δύο σωματίδια που κινούνται σε τρεις διαστάσεις, προκύπτουν έξι εξισώσεις. Μπορείτε να αλλάξετε τη θέση του σωματιδίου 1 προς την κατεύθυνση Χ,στην κατεύθυνση στοκαι προς z,και κάντε το ίδιο με το σωματίδιο 2, άρα υπάρχουν έξι εξισώσεις. Και έτσι πρέπει να είναι. Τρεις εξισώσεις καθορίζουν την επιτάχυνση του σωματιδίου 1 λόγω της δύναμης που ασκεί σε αυτό και οι άλλες τρεις προσδιορίζουν την επιτάχυνση του σωματιδίου 2 λόγω της δύναμης που ασκεί σε αυτό. Ακολουθείτε πάντα τους ίδιους κανόνες του παιχνιδιού και θα λάβετε τον νόμο του Νεύτωνα για έναν αυθαίρετο αριθμό σωματιδίων.

Είπα ότι θα πάρουμε το νόμο του Νεύτωνα. Αυτό δεν είναι απολύτως αληθές, γιατί ο νόμος του Νεύτωνα περιλαμβάνει και μη συντηρητικές δυνάμεις, όπως η τριβή. Ο Νεύτων το υποστήριξε αυτό ότιισούται με οποιοδήποτε F. Η αρχή της ελάχιστης δράσης ισχύει μόνο για συντηρητικόςσυστήματα, όπως όπου όλες οι δυνάμεις μπορούν να ληφθούν από μια δυνητική συνάρτηση. Ξέρετε όμως ότι στο μικροσκοπικό επίπεδο, δηλαδή στο βαθύτερο φυσικό επίπεδο, δεν υπάρχουν μη συντηρητικές δυνάμεις. Οι μη συντηρητικές δυνάμεις (όπως η τριβή) προκύπτουν μόνο επειδή παραμελούμε τα μικροσκοπικά πολύπλοκα φαινόμενα: απλά υπάρχουν πάρα πολλά σωματίδια για ανάλυση. Θεμελιώδηςίδιοι νόμοι μπορώεκφράζεται ως η αρχή της ελάχιστης δράσης.

Επιτρέψτε μου να προχωρήσω σε περαιτέρω γενικεύσεις. Ας υποθέσουμε ότι μας ενδιαφέρει τι θα συμβεί όταν το σωματίδιο κινηθεί σχετικιστικά. Μέχρι στιγμής δεν έχουμε αποκτήσει τη σωστή σχετικιστική εξίσωση κίνησης. Το F=ma είναι αληθές μόνο σε μη σχετικιστικές κινήσεις. Τίθεται το ερώτημα: υπάρχει αντίστοιχη αρχή της ελάχιστης δράσης στη σχετικιστική περίπτωση; Ναι, υπάρχει. Ο τύπος στη σχετικιστική περίπτωση είναι:

Το πρώτο μέρος του ολοκληρώματος δράσης είναι το γινόμενο της υπόλοιπης μάζας t 0επί από 2και στο ολοκλήρωμα της συνάρτησης ταχύτητας √ (1- v 2 /c 2 ). Τότε, αντί να αφαιρέσουμε τη δυναμική ενέργεια, έχουμε ολοκληρώματα του κλιμακωτού δυναμικού φ και του διανυσματικού δυναμικού A επί v. Φυσικά, εδώ λαμβάνονται υπόψη μόνο οι ηλεκτρομαγνητικές δυνάμεις. Όλα τα ηλεκτρικά και μαγνητικά πεδία εκφράζονται σε φ και Α. Αυτή η συνάρτηση δράσης δίνει μια πλήρη θεωρία της σχετικιστικής κίνησης ενός μεμονωμένου σωματιδίου σε ένα ηλεκτρομαγνητικό πεδίο.

Φυσικά, πρέπει να καταλάβετε ότι όπου έγραψα v, πριν κάνετε υπολογισμούς, θα πρέπει να κάνετε αντικατάσταση dx/ dt αντί v x κλπ. Επιπλέον, όπου έγραψα απλά x, y, z,πρέπει να φανταστείς τα σημεία αυτή τη στιγμή t: Χ(t), y(t), z(t). Στην πραγματικότητα, μόνο μετά από τέτοιες αντικαταστάσεις και αντικαταστάσεις του v θα λάβετε έναν τύπο για τη δράση ενός σχετικιστικού σωματιδίου. Αφήστε τους πιο έμπειρους από εσάς να προσπαθήσουν να αποδείξουν ότι αυτός ο τύπος δράσης δίνει πραγματικά τις σωστές εξισώσεις κίνησης για τη θεωρία της σχετικότητας. Επιτρέψτε μου απλώς να σας συμβουλεύσω να ξεκινήσετε απορρίπτοντας το Α, δηλαδή να κάνετε χωρίς μαγνητικά πεδία προς το παρόν. Τότε θα πρέπει να λάβετε τις συνιστώσες της εξίσωσης κίνησης dp/dt=—qVφ,όπου, όπως ίσως θυμάστε, p=mv√(1-v 2 /c 2).

Είναι πολύ πιο δύσκολο να ληφθεί υπόψη το διανυσματικό δυναμικό Α. Οι παραλλαγές γίνονται τότε ασύγκριτα πιο περίπλοκες. Αλλά στο τέλος η δύναμη αποδεικνύεται ίση με αυτή που θα έπρεπε να είναι: g(E+v × B). Αλλά διασκεδάστε με αυτό μόνοι σας.

Θα ήθελα να τονίσω ότι στη γενική περίπτωση (για παράδειγμα, στον σχετικιστικό τύπο), το ολοκλήρωμα σε δράση δεν περιλαμβάνει πλέον τη διαφορά μεταξύ κινητικής και δυνητικής ενέργειας. Αυτό ήταν κατάλληλο μόνο σε μια μη σχετικιστική προσέγγιση. Για παράδειγμα, μέλος m o c 2√(1-v 2 /c 2)-Δεν είναι αυτό που ονομάζεται κινητική ενέργεια. Το ερώτημα ποια θα πρέπει να είναι η ενέργεια για κάθε συγκεκριμένη περίπτωση μπορεί να αποφασιστεί μετά από κάποια δοκιμή και λάθος. Αυτό είναι το ίδιο πρόβλημα με τον προσδιορισμό του ποιες θα πρέπει να είναι οι εξισώσεις κίνησης. Απλά πρέπει να παίξετε με τις εξισώσεις που γνωρίζετε και να δείτε αν μπορούν να γραφτούν ως η αρχή της ελάχιστης δράσης.

Μια ακόμη σημείωση για την ορολογία. Αυτή η συνάρτηση που ενσωματώνεται με την πάροδο του χρόνου για να ληφθεί μια ενέργεια ΜΙΚΡΟ,που ονομάζεται ΛαγκραντζιανόςΛ. Αυτή είναι μια συνάρτηση που εξαρτάται μόνο από τις ταχύτητες και τις θέσεις των σωματιδίων. Άρα η αρχή της ελάχιστης δράσης γράφεται και στη φόρμα

όπου κάτω Χ ΕγώΚαι v i εννοούνται όλες οι συνιστώσες των συντεταγμένων και των ταχυτήτων. Αν ακούσετε ποτέ κάποιον να μιλά για το "Lagrangian", μιλάει για τη συνάρτηση που χρησιμοποιήθηκε για την απόκτηση μικρό. Για σχετικιστική κίνηση σε ηλεκτρομαγνητικό πεδίο

Επιπλέον, να σημειώσω ότι δεν τηλεφωνούν οι πιο σχολαστικοί και σχολαστικοί μικρόδράση. Ονομάζεται «η πρώτη κύρια λειτουργία του Χάμιλτον». Αλλά το να δώσω μια διάλεξη για την «αρχή του Χάμιλτον της ελάχιστης πρώτης κύριας λειτουργίας» ήταν πέρα από τις δυνάμεις μου. Το ονόμασα «δράση». Και επιπλέον, όλο και περισσότεροι άνθρωποι το αποκαλούν «δράση». Βλέπετε, ιστορικά η δράση ονομάστηκε κάτι άλλο που δεν είναι τόσο χρήσιμο για την επιστήμη, αλλά νομίζω ότι είναι πιο λογικό να αλλάξουμε τον ορισμό. Τώρα και εσείς θα αρχίσετε να αποκαλείτε τη νέα συνάρτηση πράξη και σύντομα όλοι θα αρχίσουν να την αποκαλούν με αυτό το απλό όνομα.

Τώρα θέλω να σας πω κάτι για το θέμα μας που μοιάζει με το σκεπτικό που είχα για την αρχή του συντομότερου χρόνου. Υπάρχει μια διαφορά στην ίδια την ουσία του νόμου που λέει ότι κάποιο ολοκλήρωμα που λαμβάνεται από το ένα σημείο στο άλλο έχει ένα ελάχιστο - ο νόμος που μας λέει κάτι για όλη την πορεία ταυτόχρονα και ο νόμος που λέει ότι όταν κινείσαι, τότε Αυτό σημαίνει ότι υπάρχει μια δύναμη που οδηγεί σε επιτάχυνση. Η δεύτερη προσέγγιση σας αναφέρει για κάθε σας βήμα, παρακολουθεί τη διαδρομή σας ίντσα προς ίντσα και η πρώτη δίνει αμέσως κάποια γενική δήλωση για ολόκληρη τη διαδρομή που διανύσατε. Μιλώντας για το φως, μιλήσαμε για τη σύνδεση μεταξύ αυτών των δύο προσεγγίσεων. Τώρα θέλω να σας εξηγήσω γιατί πρέπει να υπάρχουν διαφορικοί νόμοι εάν υπάρχει μια τέτοια αρχή - η αρχή της ελάχιστης δράσης. Ο λόγος είναι αυτός: ας εξετάσουμε το μονοπάτι που πραγματικά διανύθηκε στο χώρο και στο χρόνο. Όπως και πριν, θα αρκεστούμε σε μία μέτρηση, ώστε να μπορούμε να σχεδιάσουμε ένα γράφημα της εξάρτησης Χαπό t. Στο αληθινό μονοπάτι μικρό φτάνει στο ελάχιστο. Ας υποθέσουμε ότι έχουμε αυτό το μονοπάτι και ότι περνάει από κάποιο σημείο ΕΝΑχώρο και χρόνο και μέσα από ένα άλλο γειτονικό σημείο σι.

Τώρα, αν ολόκληρο το ολοκλήρωμα του t 1 πριν t 2 έχει φτάσει στο ελάχιστο, είναι απαραίτητο το ολοκλήρωμα κατά μήκος ενός μικρού τμήματος από ένα έως σι ήταν επίσης ελάχιστη. Δεν μπορεί να είναι αυτό το μέρος ΕΝΑπριν σιτουλάχιστον λίγο περισσότερο από το ελάχιστο. Διαφορετικά, θα μπορούσατε να μετακινήσετε την καμπύλη εμπρός και πίσω σε αυτήν την ενότητα και να μειώσετε ελαφρώς την τιμή ολόκληρου του ολοκληρώματος.

Αυτό σημαίνει ότι οποιοδήποτε μέρος της διαδρομής θα πρέπει επίσης να παρέχει ένα ελάχιστο. Και αυτό ισχύει για οποιαδήποτε μικρά τμήματα της διαδρομής. Επομένως, η αρχή ότι ολόκληρη η διαδρομή πρέπει να δίνει ένα ελάχιστο μπορεί να διατυπωθεί λέγοντας ότι ένα απειροελάχιστο τμήμα της διαδρομής είναι επίσης μια καμπύλη στην οποία η δράση είναι ελάχιστη. Και αν πάρουμε ένα αρκετά σύντομο τμήμα της διαδρομής - μεταξύ σημείων πολύ κοντά το ένα στο άλλο ΕΝΑΚαι σι,- τότε δεν έχει σημασία πώς αλλάζει το δυναμικό από σημείο σε σημείο μακριά από αυτό το μέρος, γιατί, διανύοντας ολόκληρο το σύντομο τμήμα σας, σχεδόν ποτέ δεν μετακινείστε από αυτό το μέρος. Το μόνο πράγμα που πρέπει να λάβετε υπόψη είναι η πρώτη αλλαγή στη μικρότητα στο δυναμικό. Η απάντηση μπορεί να εξαρτάται μόνο από την παράγωγο του δυναμικού και όχι από το δυναμικό αλλού. Έτσι, μια δήλωση σχετικά με την ιδιότητα ολόκληρης της διαδρομής στο σύνολό της γίνεται μια δήλωση σχετικά με το τι συμβαίνει σε ένα σύντομο τμήμα της διαδρομής, δηλ. μια διαφορική δήλωση. Και αυτή η διαφορική διατύπωση περιλαμβάνει παράγωγα του δυναμικού, δηλαδή τη δύναμη σε ένα δεδομένο σημείο. Αυτή είναι μια ποιοτική εξήγηση της σύνδεσης μεταξύ του νόμου στο σύνολό του και του διαφορικού νόμου.

Όταν μιλήσαμε για το φως, συζητήσαμε επίσης το ερώτημα: πώς βρίσκει ένα σωματίδιο το σωστό μονοπάτι; Από διαφορετική άποψη, αυτό είναι εύκολο να γίνει κατανοητό. Κάθε στιγμή το σωματίδιο βιώνει επιτάχυνση και ξέρει μόνο τι υποτίθεται ότι πρέπει να κάνει εκείνη τη στιγμή. Αλλά όλα τα ένστικτά σας για την αιτία και το αποτέλεσμα επανεμφανίζονται όταν ακούτε ότι ένα σωματίδιο «αποφασίζει» ποιο μονοπάτι να ακολουθήσει, επιδιώκοντας την ελάχιστη δράση. Δεν «μυρίζει» τα γειτονικά μονοπάτια, ανακαλύπτοντας σε τι θα οδηγήσουν - περισσότερο ή λιγότερο δράση; Όταν τοποθετήσαμε μια οθόνη στο μονοπάτι του φωτός, έτσι ώστε τα φωτόνια να μην μπορούν να δοκιμάσουν όλα τα μονοπάτια, ανακαλύψαμε ότι δεν μπορούσαν να αποφασίσουν ποιο μονοπάτι να ακολουθήσουν και πήραμε το φαινόμενο της περίθλασης.

Ισχύει όμως αυτό και για τους μηχανικούς; Είναι αλήθεια ότι ένα σωματίδιο όχι μόνο «πηγαίνει στο σωστό δρόμο», αλλά επανεξετάζει όλες τις άλλες πιθανές τροχιές; Και τι γίνεται αν βάζοντας εμπόδια στο πέρασμά του δεν του επιτρέψουμε να κοιτάξει μπροστά, τότε θα πάρουμε κάποιο είδος αναλόγου του φαινομένου της περίθλασης; Το πιο υπέροχο σε όλα αυτά είναι ότι όλα είναι πραγματικά έτσι. Αυτό ακριβώς λένε οι νόμοι της κβαντικής μηχανικής. Επομένως, η αρχή της ελάχιστης δράσης μας δεν είναι πλήρως διατυπωμένη. Δεν συνίσταται στο γεγονός ότι το σωματίδιο επιλέγει το μονοπάτι της ελάχιστης δράσης, αλλά στο ότι «αισθάνεται» όλα τα γειτονικά μονοπάτια και επιλέγει εκείνο κατά το οποίο η δράση είναι ελάχιστη, και η μέθοδος αυτής της επιλογής είναι παρόμοια με την τρόπο με τον οποίο το φως επιλέγει το συντομότερο χρόνο. Θυμάστε ότι ο τρόπος με τον οποίο το φως επιλέγει το συντομότερο χρόνο είναι ο εξής: αν το φως ακολουθήσει μια διαδρομή που απαιτεί διαφορετικό χρόνο, θα φτάσει με διαφορετική φάση. Και το συνολικό πλάτος σε κάποιο σημείο είναι το άθροισμα των συνεισφορών του πλάτους για όλα τα μονοπάτια κατά μήκος των οποίων το φως μπορεί να το φτάσει. Όλα εκείνα τα μονοπάτια των οποίων οι φάσεις διαφέρουν έντονα δεν αποδίδουν τίποτα μετά την προσθήκη. Αλλά αν καταφέρετε να βρείτε ολόκληρη την ακολουθία των μονοπατιών, οι φάσεις των οποίων είναι σχεδόν ίδιες, τότε οι μικρές συνεισφορές θα αθροιστούν και στο σημείο άφιξης το συνολικό πλάτος θα λάβει μια αξιοσημείωτη τιμή. Το πιο σημαντικό μονοπάτι είναι αυτό κοντά στο οποίο υπάρχουν πολλά κοντινά μονοπάτια που δίνουν την ίδια φάση.

Το ίδιο ακριβώς συμβαίνει και στην κβαντομηχανική. Η πλήρης κβαντική μηχανική (μη σχετικιστική και παραμελημένη σπιν ηλεκτρονίων) λειτουργεί ως εξής: η πιθανότητα ένα σωματίδιο να φύγει από ένα σημείο 1 στη στιγμή t 1, θα φτάσει στο σημείο 2 στη στιγμή t 2 , ίσο με το τετράγωνο του πλάτους πιθανότητας. Το συνολικό πλάτος μπορεί να γραφτεί ως το άθροισμα των πλατών για όλες τις πιθανές διαδρομές—για οποιαδήποτε διαδρομή άφιξης. Για οποιονδηποτε Χ(t), που θα μπορούσε να συμβεί για οποιαδήποτε νοητή τροχιά, πρέπει να υπολογιστεί το πλάτος. Στη συνέχεια πρέπει να διπλωθούν όλα. Τι λαμβάνουμε ως πλάτος πιθανότητας μιας συγκεκριμένης διαδρομής; Το ολοκλήρωμα δράσης μας μας λέει ποιο πρέπει να είναι το πλάτος μιας μεμονωμένης διαδρομής. Το πλάτος είναι ανάλογο e tS/h, Οπου μικρό - δράση σε αυτό το μονοπάτι. Αυτό σημαίνει ότι αν αναπαραστήσουμε τη φάση του πλάτους ως μιγαδικό αριθμό, τότε η γωνία φάσης θα είναι ίση με μικρό/ η. Δράση μικρό έχει τη διάσταση της ενέργειας με την πάροδο του χρόνου, και η σταθερά του Planck έχει την ίδια διάσταση. Αυτή είναι η σταθερά που καθορίζει πότε χρειάζεται κβαντομηχανική.

Και έτσι λειτουργούν όλα. Αφήστε δράση για όλα τα μονοπάτια μικρό θα είναι πολύ μεγάλο σε σύγκριση με τον αριθμό η. Αφήστε κάποια διαδρομή να οδηγήσει σε μια συγκεκριμένη τιμή πλάτους. Η φάση του διπλανού μονοπατιού θα είναι τελείως διαφορετική, γιατί με ένα τεράστιο μικρό έστω και μικρές αλλαγές μικρό αλλαγή φάσης απότομα (άλλωστε ηεξαιρετικά λίγο). Αυτό σημαίνει ότι τα γειτονικά μονοπάτια συνήθως σβήνουν τη συμβολή τους όταν προστίθενται. Και μόνο σε μια περιοχή αυτό δεν ισχύει - σε αυτήν όπου τόσο το μονοπάτι όσο και ο γείτονάς του - και οι δύο, σε μια πρώτη προσέγγιση, έχουν την ίδια φάση (ή, πιο συγκεκριμένα, σχεδόν την ίδια δράση, που ποικίλλει εντός η).Μόνο τέτοιες διαδρομές λαμβάνονται υπόψη. Και στην περιοριστική περίπτωση, όταν η σταθερά του Planck ητείνει στο μηδέν, οι σωστοί κβαντομηχανικοί νόμοι μπορούν να συνοψιστούν λέγοντας: «Ξεχάστε όλα αυτά τα πλάτη πιθανότητας. Το σωματίδιο στην πραγματικότητα κινείται κατά μήκος μιας ειδικής διαδρομής - ακριβώς αυτή κατά μήκος της οποίας μικρό σε μια πρώτη προσέγγιση δεν αλλάζει." Αυτή είναι η σύνδεση μεταξύ της αρχής της ελάχιστης δράσης και της κβαντικής μηχανικής. Το γεγονός ότι η κβαντομηχανική μπορεί να διατυπωθεί με αυτόν τον τρόπο ανακαλύφθηκε το 1942 από έναν μαθητή του ίδιου καθηγητή, τον κ. Bader, για τον οποίο σας είπα. [Η κβαντική μηχανική διατυπώθηκε αρχικά χρησιμοποιώντας μια διαφορική εξίσωση για το πλάτος (Schrödinger) καθώς και ορισμένα μαθηματικά πινάκων (Heisenberg).]

Τώρα θέλω να μιλήσω για άλλες αρχές του ελάχιστου στη φυσική. Υπάρχουν πολλές ενδιαφέρουσες αρχές αυτού του είδους. Δεν θα τα απαριθμήσω όλα, αλλά θα αναφέρω μόνο ένα ακόμη. Αργότερα, όταν φτάσουμε σε ένα φυσικό φαινόμενο για το οποίο υπάρχει μια εξαιρετική ελάχιστη αρχή, θα σας μιλήσω γι' αυτό. Τώρα θέλω να δείξω ότι δεν είναι απαραίτητο να περιγράψουμε την ηλεκτροστατική χρησιμοποιώντας μια διαφορική εξίσωση για το πεδίο. Αντίθετα, μπορεί κανείς να απαιτήσει κάποιο ολοκλήρωμα να έχει μέγιστο ή ελάχιστο. Αρχικά, ας πάρουμε την περίπτωση όταν η πυκνότητα φορτίου είναι γνωστή παντού, αλλά πρέπει να βρούμε το δυναμικό φ σε οποιοδήποτε σημείο του χώρου. Γνωρίζετε ήδη ότι η απάντηση πρέπει να είναι:

Ένας άλλος τρόπος για να πούμε το ίδιο πράγμα είναι να αξιολογήσουμε το ολοκλήρωμα U*

αυτό είναι ένα ολοκλήρωμα όγκου. Λαμβάνεται σε όλο τον χώρο. Με σωστή κατανομή δυναμικού φ (Χ, y,z) αυτή η έκφραση φτάνει στο ελάχιστο.

Μπορούμε να δείξουμε ότι και οι δύο αυτές δηλώσεις σχετικά με την ηλεκτροστατική είναι ισοδύναμες. Ας υποθέσουμε ότι επιλέξαμε μια αυθαίρετη συνάρτηση φ. Θέλουμε να δείξουμε ότι όταν πάρουμε ως φ τη σωστή τιμή του δυναμικού _φ συν μια μικρή απόκλιση f, τότε στην πρώτη τάξη μικρότητας η μεταβολή στο U* θα είναι ίσο με μηδέν. Γράφουμε λοιπόν

εδώ το φ είναι αυτό που ψάχνουμε. αλλά θα μεταβάλλουμε το φ για να δούμε τι πρέπει να είναι για να γίνει η παραλλαγή U* αποδείχθηκε ότι ήταν της πρώτης τάξης της μικρότητας. Στην πρώτη θητεία U* πρέπει να γράψουμε

Αυτό πρέπει να ενσωματωθεί από x, yκαι από z. Και εδώ το ίδιο κόλπο προτείνεται: για να απαλλαγούμε df/ dx, θα ενσωματωθούμε ξανά Χσε μέρη. Αυτό θα οδηγήσει σε πρόσθετη διαφοροποίησηφ σε σχέση με Χ.Αυτή είναι η ίδια βασική ιδέα με την οποία απαλλαγήκαμε από τα παράγωγα σε σχέση με t. Χρησιμοποιούμε την ισότητα

Ο ολοκληρωμένος όρος είναι μηδέν επειδή θεωρούμε ότι η f είναι μηδέν στο άπειρο. (Αυτό αντιστοιχεί στο η εξαφανίζεται ως t 1 Και t 2 . Άρα η αρχή μας διατυπώνεται ακριβέστερα ως εξής: U* για το δικαίωμα φ λιγότερο από οποιοδήποτε άλλο φ(x, y,z), έχοντας τις ίδιες τιμές στο άπειρο.) Τότε θα κάνουμε το ίδιο με στοκαι με z. Το αναπόσπαστο ΔU* μας θα μετατραπεί σε

Για να είναι αυτή η μεταβολή ίση με μηδέν για οποιαδήποτε αυθαίρετη f, ο συντελεστής f πρέπει να είναι ίσος με μηδέν. Που σημαίνει,

Επιστρέψαμε στην παλιά μας εξίσωση. Αυτό σημαίνει ότι η «ελάχιστη» πρότασή μας είναι σωστή. Μπορεί να γενικευτεί εάν οι υπολογισμοί τροποποιηθούν ελαφρώς. Ας πάμε πίσω και ας ενσωματώσουμε μέρος προς μέρος, χωρίς να περιγράψουμε τα πάντα συνιστώσα προς συστατικό. Ας ξεκινήσουμε γράφοντας την ακόλουθη ισότητα:

Διαφοροποιώντας την αριστερή πλευρά, μπορώ να δείξω ότι είναι ακριβώς ίση με τη δεξιά. Αυτή η εξίσωση είναι κατάλληλη για την πραγματοποίηση ολοκλήρωσης ανά εξαρτήματα. Στο ολοκλήρωμά μας ΔU* αντικαθιστούμε Vφ*Vf nκαι fV 2 φ+V*(fVφ) και στη συνέχεια ενσωματώστε αυτό στον όγκο. Ο όρος απόκλισης μετά την ολοκλήρωση στον όγκο αντικαθίσταται από ένα ολοκλήρωμα στην επιφάνεια:

Και αφού ενσωματώνουμε σε ολόκληρο τον χώρο, η επιφάνεια σε αυτό το ολοκλήρωμα βρίσκεται στο άπειρο. Αυτό σημαίνει f=0, και έχουμε το ίδιο αποτέλεσμα.

Μόνο τώρα αρχίζουμε να καταλαβαίνουμε πώς να λύνουμε προβλήματα στα οποία βρισκόμαστε δεν ξέρουμεόπου βρίσκονται όλες οι χρεώσεις. Ας έχουμε αγωγούς στους οποίους κατανέμονται με κάποιο τρόπο οι χρεώσεις. Εάν τα δυναμικά σε όλους τους αγωγούς είναι σταθερά, τότε η ελάχιστη αρχή μας εξακολουθεί να ισχύει. Ένταξη σε U* θα σχεδιάσουμε μόνο κατά μήκος της περιοχής που βρίσκεται έξω από όλους τους αγωγούς. Επειδή όμως δεν μπορούμε να αλλάξουμε το (φ) στους αγωγούς, τότε στην επιφάνειά τους f = 0, και την επιφάνεια αναπόσπαστο

πρέπει να γίνονται μόνο στα κενά μεταξύ των αγωγών. Και, φυσικά, παίρνουμε ξανά την εξίσωση Poisson

Δείξαμε λοιπόν ότι το αρχικό μας ολοκλήρωμα U* φτάνει στο ελάχιστο ακόμη και όταν υπολογίζεται στο διάστημα μεταξύ των αγωγών, καθένας από τους οποίους βρίσκεται σε σταθερό δυναμικό [αυτό σημαίνει ότι κάθε δοκιμαστική συνάρτηση φ(g, y,z) πρέπει να είναι ίσο με το καθορισμένο δυναμικό αγωγού όταν (x, y,z) - σημεία της επιφάνειας του αγωγού]. Υπάρχει μια ενδιαφέρουσα ειδική περίπτωση όταν τα φορτία εντοπίζονται μόνο σε αγωγούς. Επειτα

και η ελάχιστη αρχή μας λέει ότι στην περίπτωση που κάθε αγωγός έχει το δικό του προκαθορισμένο δυναμικό, τα δυναμικά στα μεταξύ τους διαστήματα ρυθμίζονται έτσι ώστε το ολοκλήρωμα U* αποδεικνύεται όσο το δυνατόν μικρότερο. Τι είδους ολοκλήρωμα είναι αυτό; Ο όρος Vφ είναι το ηλεκτρικό πεδίο. Αυτό σημαίνει ότι το ολοκλήρωμα είναι ηλεκτροστατική ενέργεια. Το σωστό πεδίο είναι το μόνο που, από όλα τα πεδία που λαμβάνονται ως βαθμίδα δυναμικού, έχει τη χαμηλότερη συνολική ενέργεια.

Θα ήθελα να χρησιμοποιήσω αυτό το αποτέλεσμα για να λύσω κάποιο συγκεκριμένο πρόβλημα και να σας δείξω ότι όλα αυτά τα πράγματα έχουν πραγματική πρακτική σημασία. Ας υποθέσουμε ότι πήρα δύο αγωγούς με τη μορφή ενός κυλινδρικού πυκνωτή.

Ο εσωτερικός αγωγός έχει ένα δυναμικό ίσο, ας πούμε, V, και για το εξωτερικό - μηδέν. Έστω η ακτίνα του εσωτερικού αγωγού ίση με ΕΝΑ,και εξωτερικό - σι.Τώρα μπορούμε να υποθέσουμε ότι η κατανομή των δυναμικών μεταξύ τους είναι όποιος.Αν όμως πάρουμε σωστόςτιμή του φ και υπολογίστε
(ε 0 /2) ∫ (Vφ) 2 dVτότε η ενέργεια του συστήματος θα πρέπει να είναι 1/2CV 2.

Έτσι χρησιμοποιώντας την αρχή μας μπορείτε να υπολογίσετε την χωρητικότητα ΜΕ.Εάν πάρουμε μια εσφαλμένη κατανομή δυναμικού και προσπαθήσουμε να υπολογίσουμε την χωρητικότητα του πυκνωτή χρησιμοποιώντας αυτή τη μέθοδο, θα καταλήξουμε σε μια υπερβολικά μεγάλη τιμή χωρητικότητας για μια σταθερή V. Οποιοδήποτε εκτιμώμενο δυναμικό φ που δεν συμπίπτει ακριβώς με την πραγματική του τιμή θα οδηγήσει επίσης σε λανθασμένη τιμή C, μεγαλύτερη από την απαραίτητη. Αλλά εάν το εσφαλμένα επιλεγμένο δυναμικό cp εξακολουθεί να είναι μια κατά προσέγγιση προσέγγιση, τότε η χωρητικότητα ΜΕθα αποδειχθεί με καλή ακρίβεια, γιατί το σφάλμα στο C είναι τιμή δεύτερης τάξης σε σύγκριση με το σφάλμα στο φ.

Ας υποθέσουμε ότι δεν γνωρίζω την χωρητικότητα του κυλινδρικού πυκνωτή. Τότε, για να την αναγνωρίσω, μπορώ να χρησιμοποιήσω αυτήν την αρχή. Απλώς θα δοκιμάσω διαφορετικές συναρτήσεις του φ ως δυναμικό μέχρι να πετύχω τη χαμηλότερη τιμή ΜΕ.Ας πούμε, για παράδειγμα, ότι έχω επιλέξει ένα δυναμικό που αντιστοιχεί σε ένα σταθερό πεδίο. (Γνωρίζετε, φυσικά, ότι το πεδίο εδώ δεν είναι στην πραγματικότητα σταθερό· ποικίλλει ως 1/r) Εάν το πεδίο είναι σταθερό, αυτό σημαίνει ότι το δυναμικό εξαρτάται γραμμικά από την απόσταση. Για να είναι η τάση στους αγωγούς όπως απαιτείται, η συνάρτηση φ πρέπει να έχει τη μορφή

Αυτή η συνάρτηση είναι ίση με V στο r=a,μηδέν στο r =β,και ανάμεσά τους υπάρχει μια σταθερή κλίση ίση με - V/(σι—ΕΝΑ).Έτσι, για να προσδιορίσουμε το ολοκλήρωμα U*, χρειάζεται απλώς να πολλαπλασιάσετε το τετράγωνο αυτής της διαβάθμισης επί ε o /2 και να ενσωματώσετε σε ολόκληρο τον όγκο. Ας κάνουμε αυτόν τον υπολογισμό για έναν κύλινδρο μοναδιαίου μήκους. Στοιχείο όγκου στην ακτίνα rισούται με 2πrdr. Πραγματοποιώντας την ενσωμάτωση, διαπιστώνω ότι η πρώτη μου δοκιμή δίνει την ακόλουθη χωρητικότητα:

Παίρνω λοιπόν έναν τύπο χωρητικότητας, ο οποίος, αν και λανθασμένος, είναι κάποιου είδους προσέγγιση:

Φυσικά είναι διαφορετικό από τη σωστή απάντηση C=2πε 0 /ln (b/a),αλλά γενικά δεν είναι τόσο κακό. Ας προσπαθήσουμε να το συγκρίνουμε με τη σωστή απάντηση για πολλές τιμές β/α.Οι αριθμοί που υπολόγισα φαίνονται στον παρακάτω πίνακα.

Ακόμη και όταν β/α=2(και αυτό ήδη οδηγεί σε αρκετά μεγάλες διαφορές μεταξύ των σταθερών και γραμμικών πεδίων), εξακολουθώ να έχω μια αρκετά βατή προσέγγιση. Η απάντηση φυσικά, όπως ήταν αναμενόμενο, είναι λίγο υπερβολική. Αλλά αν ένα λεπτό σύρμα τοποθετηθεί μέσα σε έναν μεγάλο κύλινδρο, τότε όλα φαίνονται πολύ χειρότερα. Τότε το πεδίο αλλάζει πολύ και η αντικατάστασή του με ένα σταθερό πεδίο δεν οδηγεί σε τίποτα καλό. Όταν b/a = 100, υπερεκτιμούμε την απάντηση σχεδόν δύο φορές. Για τα μικρά β/αη κατάσταση φαίνεται πολύ καλύτερη. Στο αντίθετο όριο, όταν το κενό μεταξύ των αγωγών δεν είναι πολύ μεγάλο (ας πούμε, για b/a = 1,1), ένα σταθερό πεδίο αποδεικνύεται ότι είναι μια πολύ καλή προσέγγιση, δίνει την τιμή ΜΕακρίβεια στα δέκατα του τοις εκατό.

Τώρα θα σας πω πώς να βελτιώσετε αυτόν τον υπολογισμό. (Η απάντηση για τον κύλινδρο είναι, φυσικά, διάσημος,αλλά η ίδια μέθοδος λειτουργεί για ορισμένα άλλα ασυνήθιστα σχήματα πυκνωτών για τα οποία μπορεί να μην γνωρίζετε τη σωστή απάντηση.) Το επόμενο βήμα είναι να βρείτε μια καλύτερη προσέγγιση για το άγνωστο πραγματικό δυναμικό φ. Ας υποθέσουμε ότι μπορείτε να δοκιμάσετε τη σταθερά συν τον εκθέτη φ, κ.λπ. Αλλά πώς ξέρετε ότι έχετε την καλύτερη προσέγγιση εάν δεν γνωρίζετε το αληθινό φ; Απάντηση:Μετρήστε το ΜΕ;όσο πιο χαμηλά είναι, τόσο πιο κοντά στην αλήθεια. Ας δοκιμάσουμε αυτή την ιδέα. Έστω το δυναμικό όχι γραμμικό, αλλά, ας πούμε, τετραγωνικό στο r, και το ηλεκτρικό πεδίο όχι σταθερό, αλλά γραμμικό. Το περισσότερο γενικόςτετραγωνική μορφή, που μετατρέπεται σε φ=Ο όταν r=βκαι σε φ=F στο r=a,είναι αυτό:

όπου α είναι ένας σταθερός αριθμός. Αυτή η φόρμουλα είναι λίγο πιο περίπλοκη από την προηγούμενη. Περιλαμβάνει και έναν τετραγωνικό και έναν γραμμικό όρο. Είναι πολύ εύκολο να πάρεις χωράφι από αυτό. Είναι ίσο με απλό

Τώρα αυτό πρέπει να τετραγωνιστεί και να ενσωματωθεί στον τόμο. Αλλά περίμενε ένα λεπτό. Τι πρέπει να πάρω για το α; Μπορώ να θεωρήσω το f ως παραβολή, αλλά ποια; Να τι θα κάνω: να υπολογίσω τη χωρητικότητα στο αυθαίρετος α.θα πάρω

Αυτό φαίνεται λίγο μπερδεμένο, αλλά έτσι αποδεικνύεται μετά την ενσωμάτωση του τετραγώνου του γηπέδου. Τώρα μπορώ να διαλέξω μόνος μου. Ξέρω ότι η αλήθεια βρίσκεται χαμηλότερα από οτιδήποτε πρόκειται να υπολογίσω. Ό,τι και να βάλω στη θέση του α, η απάντηση θα είναι ακόμα πολύ μεγάλη. Αν όμως συνεχίσω το παιχνίδι μου με το α και προσπαθήσω να πετύχω τη χαμηλότερη δυνατή τιμή ΜΕ,τότε αυτή η χαμηλότερη τιμή θα είναι πιο κοντά στην αλήθεια από οποιαδήποτε άλλη τιμή. Επομένως, τώρα πρέπει να επιλέξω το α έτσι ώστε η τιμή ΜΕέχει φτάσει στο ελάχιστο. Όσον αφορά τον συνηθισμένο διαφορικό λογισμό, είμαι πεπεισμένος ότι το ελάχιστο ΜΕθα είναι όταν α =— 2 σι/(β+ένα). Αντικαθιστώντας αυτήν την τιμή στον τύπο, παίρνω τη μικρότερη χωρητικότητα

Κατάλαβα τι δίνει αυτός ο τύπος ΜΕσε διαφορετικές τιμές β/α.Ονόμασα αυτούς τους αριθμούς ΜΕ(τετραγωνικός). Εδώ είναι ένας πίνακας που συγκρίνει ΜΕ(τετραγωνικό) με ΜΕ(αληθής).

Για παράδειγμα, όταν η αναλογία ακτίνας είναι 2:1, παίρνω 1,444. Αυτή είναι μια πολύ καλή προσέγγιση της σωστής απάντησης, 1,4423. Ακόμη και με μεγάλα Ναιη προσέγγιση παραμένει αρκετά καλή—πολύ καλύτερη από την πρώτη προσέγγιση. Παραμένει ανεκτή (υπερεκτιμάται μόνο κατά 10%) ακόμη και με b/a = 10: 1. Μια μεγάλη απόκλιση εμφανίζεται μόνο σε αναλογία 100: 1. Παίρνω ΜΕίσο με 0,346 αντί για 0,267. Από την άλλη, για αναλογία ακτίνας 1,5 η συμφωνία είναι εξαιρετική, και για b/a=1,1η απάντηση είναι 10,492065 αντί για το αναμενόμενο 10,492070. Εκεί που θα περίμενες μια καλή απάντηση, αποδεικνύεται πολύ, πολύ καλό.

Έδωσα όλα αυτά τα παραδείγματα, πρώτον, για να δείξω τη θεωρητική αξία της αρχής της ελάχιστης δράσης και γενικά όλων των αρχών του ελάχιστου και, δεύτερον, για να σας δείξω την πρακτική χρησιμότητά τους, και καθόλου για να υπολογίσετε την ικανότητα που έχουμε ήδη ξέρουμε πολύ καλά. Για οποιοδήποτε άλλο σχήμα, μπορείτε να δοκιμάσετε ένα κατά προσέγγιση πεδίο με μερικές άγνωστες παραμέτρους (όπως το α) και να τις προσαρμόσετε στο ελάχιστο. Θα λάβετε ανώτερα αριθμητικά αποτελέσματα σε προβλήματα που δεν μπορούν να επιλυθούν διαφορετικά.

Το υπακούουν και επομένως αυτή η αρχή είναι μια από τις βασικές διατάξεις της σύγχρονης φυσικής. Οι εξισώσεις κίνησης που λαμβάνονται με τη βοήθειά του ονομάζονται εξισώσεις Euler-Lagrange.

Η πρώτη διατύπωση της αρχής δόθηκε από τον P. Maupertuis το έτος, επισημαίνοντας αμέσως την καθολική φύση της, θεωρώντας την εφαρμόσιμη στην οπτική και τη μηχανική. Από αυτή την αρχή έβγαλε τους νόμους της ανάκλασης και της διάθλασης του φωτός.

Ιστορία

Ο Maupertuis κατέληξε σε αυτήν την αρχή από την αίσθηση ότι η τελειότητα του Σύμπαντος απαιτεί μια ορισμένη οικονομία στη φύση και έρχεται σε αντίθεση με κάθε άχρηστη δαπάνη ενέργειας. Η φυσική κίνηση πρέπει να είναι τέτοια που να κάνει μια ορισμένη ποσότητα ελάχιστη. Το μόνο που έπρεπε να κάνει ήταν να βρει αυτή την αξία, την οποία συνέχισε να κάνει. Ήταν το γινόμενο της διάρκειας (χρόνου) της κίνησης μέσα στο σύστημα κατά διπλάσια τιμή, που τώρα ονομάζουμε κινητική ενέργεια του συστήματος.

Euler (σε "Réflexions sur quelques loix générales de la nature", 1748) υιοθετεί την αρχή της ελάχιστης δράσης, αποκαλώντας τη δράση «προσπάθεια». Η έκφρασή του σε στατική αντιστοιχεί σε αυτό που θα ονομάζαμε τώρα δυναμική ενέργεια, έτσι ώστε η δήλωση της ελάχιστης δράσης του στη στατική είναι ισοδύναμη με την συνθήκη ελάχιστης δυναμικής ενέργειας για μια διαμόρφωση ισορροπίας.

Στην κλασική μηχανική

Η αρχή της ελάχιστης δράσης χρησιμεύει ως η θεμελιώδης και τυπική βάση των διαμορφώσεων της μηχανικής Lagrangian και Hamilton.

Αρχικά ας δούμε την κατασκευή ως εξής: Λαγκρανζική μηχανική. Χρησιμοποιώντας το παράδειγμα ενός φυσικού συστήματος με έναν βαθμό ελευθερίας, ας υπενθυμίσουμε ότι μια ενέργεια είναι μια συνάρτηση σε σχέση με (γενικευμένες) συντεταγμένες (στην περίπτωση ενός βαθμού ελευθερίας - μία συντεταγμένη), δηλαδή εκφράζεται μέσω έτσι ώστε κάθε πιθανή εκδοχή της συνάρτησης να σχετίζεται με έναν ορισμένο αριθμό - μια ενέργεια (με αυτή την έννοια, μπορούμε να πούμε ότι μια ενέργεια ως συνάρτηση είναι ένας κανόνας που επιτρέπει σε κάθε δεδομένη συνάρτηση να υπολογίσει έναν εντελώς συγκεκριμένο αριθμό - που ονομάζεται επίσης μια δράση). Η δράση μοιάζει με:

όπου είναι το Lagrangian του συστήματος, ανάλογα με τη γενικευμένη συντεταγμένη, η πρώτη του παράγωγος ως προς το χρόνο, και επίσης, ενδεχομένως, ρητά στον χρόνο. Εάν το σύστημα έχει μεγαλύτερο αριθμό βαθμών ελευθερίας, τότε ο Λαγκραντζιανός εξαρτάται από μεγαλύτερο αριθμό γενικευμένων συντεταγμένων και των πρώτων παραγώγων τους ως προς το χρόνο. Έτσι, η δράση είναι βαθμωτή λειτουργική ανάλογα με την τροχιά του σώματος.

Το γεγονός ότι η ενέργεια είναι βαθμωτή καθιστά εύκολη τη γραφή της σε οποιεσδήποτε γενικευμένες συντεταγμένες, το κύριο πράγμα είναι ότι η θέση (διαμόρφωση) του συστήματος χαρακτηρίζεται ξεκάθαρα από αυτές (για παράδειγμα, αντί για καρτεσιανές συντεταγμένες, αυτές μπορεί να είναι πολικές συντεταγμένες, αποστάσεις μεταξύ σημείων του συστήματος, γωνίες ή συναρτήσεις τους κ.λπ. .δ.).

Η δράση μπορεί να υπολογιστεί για μια εντελώς αυθαίρετη τροχιά, όσο «άγρια» και «αφύσικη» κι αν είναι. Ωστόσο, στην κλασική μηχανική, ανάμεσα σε ολόκληρο το σύνολο των πιθανών τροχιών, υπάρχει μόνο μία κατά μήκος της οποίας θα κινηθεί πραγματικά το σώμα. Η αρχή της ακίνητης δράσης δίνει ακριβώς την απάντηση στο ερώτημα πώς θα κινηθεί πραγματικά το σώμα:

Αυτό σημαίνει ότι εάν δοθεί το Lagrangian του συστήματος, τότε χρησιμοποιώντας τον λογισμό των παραλλαγών μπορούμε να καθορίσουμε πώς ακριβώς θα κινηθεί το σώμα παίρνοντας πρώτα τις εξισώσεις κίνησης - τις εξισώσεις Euler-Lagrange και στη συνέχεια λύνοντάς τις. Αυτό επιτρέπει όχι μόνο τη σοβαρή γενίκευση της διατύπωσης της μηχανικής, αλλά και την επιλογή των πιο βολικών συντεταγμένων για κάθε συγκεκριμένο πρόβλημα, χωρίς να περιορίζεται στα καρτεσιανά, που μπορεί να είναι πολύ χρήσιμα για τη λήψη των απλούστερων και πιο εύκολα λυμένων εξισώσεων.

πού είναι η συνάρτηση Hamilton αυτού του συστήματος; - (γενικευμένες) συντεταγμένες, - συζευγμένες (γενικευμένες) παρορμήσεις, οι οποίες μαζί χαρακτηρίζουν σε κάθε δεδομένη χρονική στιγμή τη δυναμική κατάσταση του συστήματος και, καθεμία συνάρτηση του χρόνου, χαρακτηρίζοντας έτσι την εξέλιξη (κίνηση) του συστήματος. Σε αυτή την περίπτωση, για να ληφθούν οι εξισώσεις κίνησης του συστήματος με τη μορφή των κανονικών εξισώσεων του Hamilton, είναι απαραίτητο να μεταβληθεί η ενέργεια που γράφτηκε με αυτόν τον τρόπο ανεξάρτητα για όλους και .

Πρέπει να σημειωθεί ότι εάν από τις συνθήκες του προβλήματος είναι καταρχήν δυνατό να βρεθεί ο νόμος της κίνησης, τότε αυτό γίνεται αυτόματα Δενσημαίνει ότι είναι δυνατό να κατασκευαστεί μια συνάρτηση που παίρνει μια σταθερή τιμή κατά την πραγματική κίνηση. Ένα παράδειγμα είναι η κοινή κίνηση ηλεκτρικών φορτίων και μονοπόλων -μαγνητικά φορτία- σε ένα ηλεκτρομαγνητικό πεδίο. Οι εξισώσεις κίνησής τους δεν μπορούν να προκύψουν από την αρχή της ακίνητης δράσης. Ομοίως, ορισμένα συστήματα Χαμιλτονίου έχουν εξισώσεις κίνησης που δεν μπορούν να προκύψουν από αυτήν την αρχή.

Παραδείγματα

Ασήμαντα παραδείγματα βοηθούν στην αξιολόγηση της χρήσης της αρχής λειτουργίας μέσω των εξισώσεων Euler-Lagrange. Ελεύθερο σωματίδιο (μάζα Μκαι ταχύτητα v) στον Ευκλείδειο χώρο κινείται σε ευθεία γραμμή. Χρησιμοποιώντας τις εξισώσεις Euler-Lagrange, αυτό μπορεί να φανεί σε πολικές συντεταγμένες ως εξής. Ελλείψει δυναμικού, η συνάρτηση Lagrange είναι απλώς ίση με την κινητική ενέργεια

σε ένα ορθογώνιο σύστημα συντεταγμένων.

Στις πολικές συντεταγμένες, η κινητική ενέργεια, και επομένως η συνάρτηση Lagrange, γίνεται

Οι ακτινικές και γωνιακές συνιστώσες των εξισώσεων γίνονται, αντίστοιχα:

Επίλυση αυτών των δύο εξισώσεων

Εδώ είναι μια υπό όρους συμβολισμός για άπειρα πολλαπλή συναρτητική ολοκλήρωση σε όλες τις τροχιές x(t) και είναι η σταθερά του Planck. Τονίζουμε ότι, κατ' αρχήν, η δράση στην εκθετική εμφανίζεται (ή μπορεί να εμφανιστεί) η ίδια κατά τη μελέτη του τελεστή εξέλιξης στην κβαντομηχανική, αλλά για συστήματα που έχουν ακριβές κλασσικό (μη κβαντικό) ανάλογο, είναι ακριβώς ίση με το συνηθισμένο κλασική δράση.

Η μαθηματική ανάλυση αυτής της έκφρασης στο κλασικό όριο - για αρκετά μεγάλες, δηλαδή για πολύ γρήγορες ταλαντώσεις της φανταστικής εκθετικής - δείχνει ότι η συντριπτική πλειοψηφία όλων των πιθανών τροχιών σε αυτό το ολοκλήρωμα ακυρώνει η μία την άλλη στο όριο (τυπικά για ). Σχεδόν για οποιοδήποτε μονοπάτι υπάρχει μια διαδρομή στην οποία η μετατόπιση φάσης θα είναι ακριβώς το αντίθετο, και θα αθροίζονται ως μηδενική συμβολή. Μόνο εκείνες οι τροχιές για τις οποίες η δράση είναι κοντά στην ακραία τιμή (για τα περισσότερα συστήματα - στο ελάχιστο) δεν μειώνονται. Αυτό είναι ένα καθαρά μαθηματικό γεγονός από τη θεωρία των συναρτήσεων μιας μιγαδικής μεταβλητής. Για παράδειγμα, η μέθοδος στατικής φάσης βασίζεται σε αυτήν.

Ως αποτέλεσμα, το σωματίδιο, σε πλήρη συμφωνία με τους νόμους της κβαντικής μηχανικής, κινείται ταυτόχρονα κατά μήκος όλων των τροχιών, αλλά υπό κανονικές συνθήκες μόνο τροχιές κοντά σε ακίνητες (δηλαδή κλασικές) συμβάλλουν στις παρατηρούμενες τιμές. Δεδομένου ότι η κβαντική μηχανική μετατρέπεται σε κλασική μηχανική στο όριο των υψηλών ενεργειών, μπορούμε να υποθέσουμε ότι αυτό είναι κβαντομηχανική εξαγωγή της κλασικής αρχής της στασιμότητας της δράσης.

Στην κβαντική θεωρία πεδίου

Στην κβαντική θεωρία πεδίου εφαρμόζεται επίσης με επιτυχία η αρχή της στατικής δράσης. Η πυκνότητα Lagrangi εδώ περιλαμβάνει τους τελεστές των αντίστοιχων κβαντικών πεδίων. Αν και είναι πιο σωστό εδώ στην ουσία (με εξαίρεση το κλασικό όριο και εν μέρει τα σχεδόν κλασσικά) να μην μιλάμε για την αρχή της σταθερότητας της δράσης, αλλά για την ολοκλήρωση Feynman κατά μήκος τροχιών στη διαμόρφωση ή στο χώρο φάσης αυτών των πεδίων - χρησιμοποιώντας η μόλις αναφερθείσα Lagrange πυκνότητα.

Περαιτέρω γενικεύσεις

Ευρύτερα, μια ενέργεια νοείται ως μια συνάρτηση που ορίζει μια αντιστοίχιση από έναν χώρο διαμόρφωσης σε ένα σύνολο πραγματικών αριθμών και, γενικά, δεν χρειάζεται να είναι ολοκλήρωμα, επειδή οι μη τοπικές ενέργειες είναι κατ' αρχήν δυνατές, τουλάχιστον θεωρητικά. Επιπλέον, ένας χώρος διαμόρφωσης δεν είναι απαραίτητα ένας χώρος συναρτήσεων, επειδή μπορεί να έχει μη μεταθετική γεωμετρία.

Ιστορία

Στην κλασική μηχανική

Παραδείγματα

σε ένα ορθογώνιο σύστημα συντεταγμένων.

Στις πολικές συντεταγμένες, η κινητική ενέργεια, και επομένως η συνάρτηση Lagrange, γίνεται

Οι ακτινικές και γωνιακές συνιστώσες των εξισώσεων γίνονται, αντίστοιχα:

Επίλυση αυτών των δύο εξισώσεων

Στην κβαντική θεωρία πεδίου

Περαιτέρω γενικεύσεις

Η αρχή της ελάχιστης δράσης, που διατυπώθηκε για πρώτη φορά ακριβώς από τον Jacobi, είναι παρόμοια με την αρχή του Hamilton, αλλά λιγότερο γενική και πιο δύσκολο να αποδειχθεί. Αυτή η αρχή εφαρμόζεται μόνο στην περίπτωση που οι συνδέσεις και η συνάρτηση δύναμης δεν εξαρτώνται από το χρόνο και όταν, επομένως, υπάρχει ένα ολοκλήρωμα ζωντανής δύναμης.

Αυτό το ολοκλήρωμα έχει τη μορφή:

Η αρχή του Hamilton που αναφέρθηκε παραπάνω δηλώνει ότι η παραλλαγή του ολοκληρώματος

ισούται με μηδέν κατά τη μετάβαση της πραγματικής κίνησης σε οποιαδήποτε άλλη απείρως κοντινή κίνηση, η οποία μεταφέρει το σύστημα από την ίδια αρχική θέση στην ίδια τελική θέση στην ίδια χρονική περίοδο.

Η αρχή του Jacobi, αντίθετα, εκφράζει μια ιδιότητα κίνησης που δεν εξαρτάται από το χρόνο. Ο Jacobi θεωρεί το αναπόσπαστο

καθοριστική δράση. Η αρχή που καθιέρωσε δηλώνει ότι η μεταβολή αυτού του ολοκληρώματος είναι μηδέν όταν συγκρίνουμε την πραγματική κίνηση του συστήματος με οποιαδήποτε άλλη απείρως στενή κίνηση που οδηγεί το σύστημα από την ίδια αρχική θέση στην ίδια τελική θέση. Σε αυτή την περίπτωση, δεν δίνουμε προσοχή στη χρονική περίοδο που δαπανάται, αλλά παρατηρούμε την εξίσωση (1), δηλαδή την εξίσωση του ανθρώπινου δυναμικού με την ίδια τιμή της σταθεράς h όπως στην πραγματική κίνηση.

Αυτή η απαραίτητη προϋπόθεση για ένα άκρο οδηγεί, γενικά, σε ένα ελάχιστο ολοκλήρωμα (2), εξ ου και η ονομασία αρχή της ελάχιστης δράσης. Η ελάχιστη συνθήκη φαίνεται να είναι η πιο φυσική, αφού η τιμή του Τ είναι ουσιαστικά θετική και επομένως το ολοκλήρωμα (2) πρέπει απαραίτητα να έχει ελάχιστο. Η ύπαρξη ενός ελάχιστου μπορεί να αποδειχθεί αυστηρά εάν μόνο η χρονική περίοδος είναι αρκετά μικρή. Η απόδειξη αυτής της θέσης βρίσκεται στη διάσημη πορεία του Darboux για τη θεωρία της επιφάνειας. Εμείς, ωστόσο, δεν θα το παρουσιάσουμε εδώ και θα περιοριστούμε στην εξαγωγή της συνθήκης

432. Απόδειξη της αρχής της ελάχιστης δράσης.

Στον πραγματικό υπολογισμό συναντάμε μια δυσκολία που δεν υπάρχει στην απόδειξη του θεωρήματος του Hamilton. Η μεταβλητή t δεν παραμένει πλέον ανεξάρτητη από την παραλλαγή. επομένως παραλλαγές των q i και q. σχετίζονται με τη μεταβολή του t με μια μιγαδική σχέση που προκύπτει από την εξίσωση (1). Ο απλούστερος τρόπος για να ξεπεράσετε αυτήν τη δυσκολία είναι να αλλάξετε την ανεξάρτητη μεταβλητή, επιλέγοντας μια της οποίας οι τιμές εμπίπτουν μεταξύ σταθερών ορίων που δεν εξαρτώνται από το χρόνο. Έστω k μια νέα ανεξάρτητη μεταβλητή, τα όρια της οποίας θεωρούνται ανεξάρτητα από το t. Όταν μετακινείτε το σύστημα, οι παράμετροι και το t θα είναι συναρτήσεις αυτής της μεταβλητής

Έστω γράμματα με πρώτους q υποδηλώνουν παράγωγα των παραμέτρων q ως προς το χρόνο.

Εφόσον οι συνδέσεις, κατά την υπόθεση, δεν εξαρτώνται από το χρόνο, οι καρτεσιανές συντεταγμένες x, y, z είναι συναρτήσεις του q που δεν περιέχουν χρόνο. Επομένως, οι παράγωγοί τους θα είναι γραμμικές ομοιογενείς συναρτήσεις του q και το 7 θα είναι μια ομοιογενής τετραγωνική μορφή του q, οι συντελεστές της οποίας είναι συναρτήσεις του q. Εχουμε

Για να διακρίνουμε τα παράγωγα του q ως προς το χρόνο, δηλώνουμε, χρησιμοποιώντας παρενθέσεις, (q), τα παράγωγα του q λαμβάνονται ως προς και που τίθενται σύμφωνα με αυτό.

τότε θα έχουμε

και το ολοκλήρωμα (2), που εκφράζεται μέσω της νέας ανεξάρτητης μεταβλητής Α, θα έχει τη μορφή.

Η παράγωγος μπορεί να εξαλειφθεί χρησιμοποιώντας το θεώρημα της ζωντανής δύναμης. Πράγματι, το αναπόσπαστο του ανθρώπινου δυναμικού θα είναι

Αντικαθιστώντας αυτήν την έκφραση στον τύπο για, ανάγουμε το ολοκλήρωμα (2) στη μορφή

Το ολοκλήρωμα που ορίζει τη δράση πήρε έτσι την τελική του μορφή (3). Η συνάρτηση ολοκληρώματος είναι η τετραγωνική ρίζα της τετραγωνικής μορφής των μεγεθών

Ας δείξουμε ότι οι διαφορικές εξισώσεις των ακραίων του ολοκληρώματος (3) είναι ακριβώς οι εξισώσεις Lagrange. Οι εξισώσεις των ακραίων, με βάση τους γενικούς τύπους του λογισμού των μεταβολών, θα είναι:

Ας πολλαπλασιάσουμε τις εξισώσεις επί 2 και ας κάνουμε μερικές διαφοροποιήσεις, λαμβάνοντας υπόψη ότι δεν περιέχει, τότε παίρνουμε, αν δεν γράψουμε δείκτη,

Αυτές είναι εξισώσεις ακραίων που εκφράζονται με όρους της ανεξάρτητης μεταβλητής.Το καθήκον τώρα είναι να επιστρέψουμε στην ανεξάρτητη μεταβλητή

Εφόσον το Γ είναι ομοιογενής συνάρτηση του δεύτερου βαθμού και είναι ομοιογενής συνάρτηση του πρώτου βαθμού, έχουμε

Από την άλλη πλευρά, το θεώρημα της ζωντανής δύναμης μπορεί να εφαρμοστεί στους παράγοντες των παραγώγων στις εξισώσεις των ακραίων, γεγονός που οδηγεί, όπως είδαμε παραπάνω, στην υποκατάσταση

Ως αποτέλεσμα όλων των αντικαταστάσεων, οι εξισώσεις των ακραίων μειώνονται στη μορφή

Φτάσαμε λοιπόν στις εξισώσεις Lagrange.

433. Η περίπτωση που δεν υπάρχουν κινητήριες δυνάμεις.

Στην περίπτωση που δεν υπάρχουν κινητήριες δυνάμεις, υπάρχει εξίσωση για ζωντανή δύναμη και έχουμε

Η προϋπόθεση για το ολοκλήρωμα να είναι ελάχιστο είναι σε αυτή την περίπτωση ότι η αντίστοιχη τιμή του -10 πρέπει να είναι η μικρότερη. Έτσι, όταν δεν υπάρχουν κινητήριες δυνάμεις, τότε μεταξύ όλων των κινήσεων στις οποίες η ζωντανή δύναμη διατηρεί την ίδια δεδομένη τιμή, η πραγματική κίνηση είναι αυτή που μεταφέρει το σύστημα από την αρχική του θέση στην τελική του θέση στο συντομότερο χρόνο.

Εάν το σύστημα μειωθεί σε ένα σημείο που κινείται σε μια ακίνητη επιφάνεια, τότε η πραγματική κίνηση, μεταξύ όλων των κινήσεων στην επιφάνεια που συμβαίνουν με την ίδια ταχύτητα, είναι η κίνηση κατά την οποία το σημείο μετακινείται από την αρχική του θέση στην τελική θέση στο συντομότερος

χρονικό διάστημα. Με άλλα λόγια, ένα σημείο περιγράφει στην επιφάνεια τη συντομότερη γραμμή μεταξύ των δύο θέσεων του, δηλαδή μια γεωδαισιακή γραμμή.

434. Σημ.

Η αρχή της ελάχιστης δράσης προϋποθέτει ότι το σύστημα έχει πολλούς βαθμούς ελευθερίας, αφού αν υπήρχε μόνο ένας βαθμός ελευθερίας, τότε μια εξίσωση θα ήταν αρκετή για να καθορίσει την κίνηση. Εφόσον η κίνηση μπορεί σε αυτή την περίπτωση να προσδιοριστεί πλήρως από την εξίσωση της ζωντανής δύναμης, τότε η πραγματική κίνηση θα είναι η μόνη που ικανοποιεί αυτήν την εξίσωση και επομένως δεν μπορεί να συγκριθεί με καμία άλλη κίνηση.

Η ΛΙΓΟΤΕΡΟ ΑΠΟΤΕΛΕΣΜΑΤΙΚΗ ΑΡΧΗ

Μία από τις μεταβλητές αρχές της μηχανικής, σύμφωνα με τον Krom, για μια δεδομένη κατηγορία μηχανικών κινήσεων σε σύγκριση μεταξύ τους. σύστημα, το έγκυρο είναι αυτό για το οποίο φυσικό. μέγεθος, που ονομάζεται δράση, έχει τη μικρότερη (ακριβέστερα, ακίνητη) αξία. Συνήθως το N. d. p. χρησιμοποιείται σε μία από τις δύο μορφές.

α) Η N. d. p. με τη μορφή Hamilton - Ostrogradsky καθιερώνει ότι μεταξύ όλων των κινηματικά πιθανών κινήσεων ενός συστήματος από τη μια διαμόρφωση στην άλλη (κοντά στην πρώτη), που πραγματοποιούνται την ίδια χρονική περίοδο, η έγκυρη είναι αυτή για την οποία το Hamiltonian action S θα είναι το μικρότερο. Μαθηματικά. η έκφραση του N. d.p. σε αυτή την περίπτωση έχει τη μορφή: dS = 0, όπου d είναι το σύμβολο της ατελούς (ισόχρονης) παραλλαγής (δηλαδή, σε αντίθεση με την πλήρη παραλλαγή, ο χρόνος δεν μεταβάλλεται σε αυτήν).

β) Το N. d. p. με τη μορφή Maupertuis - Lagrange ορίζει ότι μεταξύ όλων των κινηματικά πιθανών κινήσεων ενός συστήματος από μια διαμόρφωση σε μια άλλη κοντά σε αυτό, που εκτελούνται διατηρώντας την ίδια τιμή της συνολικής ενέργειας του συστήματος, η έγκυρη είναι ότι για - Επομένως, η ενέργεια Lagrange W θα είναι η μικρότερη. Μαθηματικά. η έκφραση του N. d.p. σε αυτή την περίπτωση έχει τη μορφή DW = 0, όπου D είναι το σύμβολο της συνολικής μεταβολής (σε αντίθεση με την αρχή Hamilton-Ostrogradsky, εδώ δεν ποικίλλουν μόνο οι συντεταγμένες και οι ταχύτητες, αλλά και ο χρόνος κίνησης του σύστημα από τη μία διαμόρφωση στην άλλη) . N.d.p.v. Σε αυτή την περίπτωση, ισχύει μόνο για συντηρητικά και, επιπλέον, ολονομικά συστήματα, ενώ στην πρώτη περίπτωση, η μη συντηρητική αρχή είναι γενικότερη και, ειδικότερα, μπορεί να επεκταθεί σε μη συντηρητικά συστήματα. Για τη σύνταξη εξισώσεων μηχανικής κίνησης χρησιμοποιούνται N.D.P. συστήματα και να μελετήσει τις γενικές ιδιότητες αυτών των κινήσεων. Με μια κατάλληλη γενίκευση των εννοιών, το NDP βρίσκει εφαρμογές στη μηχανική ενός συνεχούς μέσου, στην ηλεκτροδυναμική και στο κβαντικό. μηχανική κλπ.

- το ίδιο με...
Φυσική εγκυκλοπαίδεια
- m-τελεστής, τελεστής ελαχιστοποίησης, - μέθοδος κατασκευής νέων συναρτήσεων από άλλες συναρτήσεις, που αποτελείται από τα ακόλουθα...
Μαθηματική Εγκυκλοπαίδεια
- μία από τις μεταβλητές αρχές της μηχανικής, σύμφωνα με την οποία για μια δεδομένη κατηγορία μηχανικών κινήσεων συγκρίνονται μεταξύ τους. σύστημα εκτελείται εκείνο για το οποίο η δράση είναι ελάχιστη...
Φυσικές Επιστήμες. εγκυκλοπαιδικό λεξικό
- ένας από τους πιο σημαντικούς νόμους της μηχανικής, που θεσπίστηκε από τον Ρώσο επιστήμονα M.V. Ostrogradsky...
Ρωσική Εγκυκλοπαίδεια
Λεξικό νομικών όρων
- στο συνταγματικό δίκαιο ορισμένων κρατών η αρχή σύμφωνα με την οποία οι γενικά αναγνωρισμένες αρχές και κανόνες του διεθνούς δικαίου αποτελούν αναπόσπαστο μέρος του νομικού συστήματος της αντίστοιχης χώρας...
Εγκυκλοπαίδεια Δικηγόρου
- στο συνταγματικό δίκαιο ορισμένων κρατών η αρχή σύμφωνα με την οποία οι γενικά αναγνωρισμένοι κανόνες του διεθνούς δικαίου αποτελούν αναπόσπαστο μέρος του εθνικού νομικού συστήματος...
Μεγάλο νομικό λεξικό
- η μικρότερη απόσταση από το κέντρο της εκρηκτικής γόμωσης έως την ελεύθερη επιφάνεια - γραμμή σε αντίσταση nai-malkoto - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonalala - hamgiin baga...
Λεξικό κατασκευής
- εάν είναι δυνατόν να μετακινηθούν σημεία ενός παραμορφώσιμου σώματος προς διαφορετικές κατευθύνσεις, κάθε σημείο αυτού του σώματος κινείται προς την κατεύθυνση της ελάχιστης αντίστασης...
Εγκυκλοπαιδικό Λεξικό Μεταλλουργίας
- κανόνας βάσει του οποίου τα υπάρχοντα αποθέματα συνήθως αποτιμώνται είτε στο χαμηλότερο κόστος είτε στη χαμηλότερη τιμή πώλησης...
Λεξικό επιχειρηματικών όρων
- στο συνταγματικό δίκαιο ορισμένων κρατών - η αρχή σύμφωνα με την οποία οι γενικά αναγνωρισμένες αρχές και κανόνες του διεθνούς δικαίου αποτελούν αναπόσπαστο μέρος του νομικού συστήματος του σχετικού κράτους και λειτουργούν...
Εγκυκλοπαιδικό Λεξικό Οικονομικών και Νομικών
- μία από τις μεταβλητές αρχές της μηχανικής, σύμφωνα με την οποία για μια δεδομένη κατηγορία κινήσεων ενός μηχανικού συστήματος σε σύγκριση μεταξύ τους, η έγκυρη είναι αυτή για την οποία η φυσική ποσότητα,...
- το ίδιο με την αρχή του Gauss...
Μεγάλη Σοβιετική Εγκυκλοπαίδεια
- μία από τις μεταβλητές αρχές της μηχανικής. το ίδιο με την αρχή της ελάχιστης δράσης...
Μεγάλη Σοβιετική Εγκυκλοπαίδεια
- μια από τις μεταβλητές αρχές της μηχανικής, σύμφωνα με την οποία για μια δεδομένη κατηγορία κινήσεων ενός μηχανικού συστήματος σε σύγκριση μεταξύ τους, αυτή για την οποία η δράση είναι ελάχιστη...
Μεγάλο εγκυκλοπαιδικό λεξικό
- Βιβλίο Επιλέξτε τον πιο εύκολο τρόπο δράσης, αποφεύγοντας τα εμπόδια, αποφεύγοντας τις δυσκολίες...
Φρασεολογικό λεξικό της ρωσικής λογοτεχνικής γλώσσας

«Η ΑΡΧΗ ΤΟΥ ΛΙΓΟΤΕΡΟΣ ΑΞΙΑΣ» σε βιβλία

2.5.1. Αρχή λειτουργίας της συσκευής

Από το βιβλίο Entertaining Electronics [Μη συμβατική εγκυκλοπαίδεια χρήσιμων κυκλωμάτων] συγγραφέας Κασκάροφ Αντρέι Πέτροβιτς

2.5.1. Η αρχή λειτουργίας της συσκευής Η αρχή λειτουργίας της συσκευής είναι απλή. Όταν η φωτεινή ροή που εκπέμπεται από το HL1 LED αντανακλάται από το αντικείμενο και χτυπά τον φωτοανιχνευτή, η ηλεκτρονική μονάδα, που εφαρμόζεται σε 2 μικροκυκλώματα - τον συγκριτή KR1401SA1 και το χρονόμετρο KR1006VI1, παράγει

Η αρχή της λειτουργίας του teraphim

Από το βιβλίο Μυστική Γνώση. Θεωρία και πράξη της Agni Yoga συγγραφέας Ρέριχ Έλενα Ιβάνοβνα

Η αρχή της λειτουργίας του teraphim 24.02.39 Γνωρίζετε ότι κάθε επίγνωση και αναπαράσταση οποιουδήποτε αντικειμένου μας φέρνει πιο κοντά σε αυτό. Όπως γνωρίζετε, τα ψυχικά στρώματα ενός αντικειμένου μπορούν να μεταφερθούν στο τεραφίμ του. Το αστρικό τεραφίμ των μακρινών κόσμων και

Τρεις προϋποθέσεις για την εφαρμογή του νόμου της ελάχιστης προσπάθειας

Από το βιβλίο The Wisdom of Deepak Chopra [Αποκτήστε αυτό που θέλετε ακολουθώντας τους 7 νόμους του Σύμπαντος] από τον Tim Goodman

Τρεις προϋποθέσεις για να λειτουργήσει ο Νόμος της Ελάχιστης Προσπάθειας Ας δούμε ποιες προϋποθέσεις απαιτούνται για να προσελκύσετε αυτή τη δημιουργική ροή ενέργειας από το Σύμπαν στη ζωή σας - την ενέργεια της αγάπης και επομένως για να αρχίσει να λειτουργεί στη ζωή σας ο Νόμος της Ελάχιστης Προσπάθειας .

Κεφάλαιο 19 ΑΡΧΗ ΤΟΥ Ελάχιστου ΑΠΟΤΕΛΕΣΜΑΤΟΣ

Από το βιβλίο 6. Ηλεκτροδυναμική συγγραφέας Φάινμαν Ρίτσαρντ Φίλιπς

Κεφάλαιο 19 Η ΑΡΧΗ ΤΟΥ Ελάχιστου ΑΠΟΤΕΛΕΣΜΑΤΟΣ Προσθήκη που έγινε μετά από μια διάλεξη Όταν ήμουν στο σχολείο, ο καθηγητής φυσικής μας, ονόματι Bader, με κάλεσε κάποτε μετά το μάθημα και είπε: «Φαίνεσαι σαν να είσαι τρομερά κουρασμένος από τα πάντα. ακούστε ένα ενδιαφέρον πράγμα

5. Αρχή της ελάχιστης δράσης

Από το βιβλίο Επανάσταση στη Φυσική από τον de Broglie Louis

5. Αρχή της ελάχιστης δράσης Οι εξισώσεις για τη δυναμική ενός υλικού σημείου σε ένα πεδίο δυνάμεων με δυναμικό μπορούν να ληφθούν με βάση την αρχή, η οποία σε γενικούς όρους ονομάζεται αρχή του Hamilton, ή η αρχή της ακίνητης δράσης. Σύμφωνα με αυτή την αρχή, όλων

Λειτουργική αρχή

Από το βιβλίο Locksmith's Guide to Locks από τον Phillips Bill

Αρχή λειτουργίας Η ικανότητα περιστροφής του κυλίνδρου εξαρτάται από τη θέση των ακίδων, η οποία με τη σειρά της καθορίζεται από τη βαρύτητα, τη δράση των ελατηρίων και τη δύναμη του κλειδιού (ή του κύριου κλειδιού, για πληροφορίες σχετικά με τα κύρια κλειδιά, βλέπε Κεφάλαιο 9) . Ελλείψει κλειδιού, η βαρύτητα και τα ελατήρια πιέζουν προς τα μέσα

Αρχή της σταθερής δράσης

Από το βιβλίο Μεγάλη Σοβιετική Εγκυκλοπαίδεια (ST) του συγγραφέα TSB

Αρχή της ελάχιστης δράσης

TSB

Αρχή του ελάχιστου εξαναγκασμού

Από το βιβλίο Μεγάλη Σοβιετική Εγκυκλοπαίδεια (ΝΑ) του συγγραφέα TSB

2.5.1. Λειτουργική αρχή

Από το βιβλίο Προστασία ρελέ σε δίκτυα διανομής ηλεκτρικής ενέργειας Β90 συγγραφέας Μπουλίτσεφ Αλεξάντερ Βιτάλιεβιτς

2.5.1. Αρχή λειτουργίας Σε ηλεκτρικά δίκτυα με αμφίδρομη παροχή ρεύματος και σε δίκτυα δακτυλίου, η συμβατική προστασία ρεύματος δεν μπορεί να λειτουργήσει επιλεκτικά. Για παράδειγμα, σε ένα ηλεκτρικό δίκτυο με δύο πηγές ενέργειας (Εικ. 2.15), όπου διακόπτες και προστασίες είναι εγκατεστημένοι και στις δύο πλευρές

Λειτουργική αρχή

Από το βιβλίο Turbo Suslik. Πώς να σταματήσεις να πηδάς τον εαυτό σου και να αρχίσεις να ζεις συγγραφέας Λέουσκιν Ντμίτρι

Η αρχή της δράσης «Επεξεργαστείτε αυτό» είναι, στην πραγματικότητα, ένα είδος «μακροεντολής» που, με μια φράση, εκτοξεύει μια ολόκληρη δέσμη διεργασιών στο υποσυνείδητο, σκοπός των οποίων είναι η επεξεργασία του επιλεγμένου νοητικού υλικού. Αυτός ο ίδιος ο χειριστής περιλαμβάνει 7 διαφορετικές μονάδες, μερικές από τις οποίες

Πώς να ξεκινήσετε να ακολουθείτε τον νόμο της ελάχιστης προσπάθειας: Τρεις απαραίτητες ενέργειες

Από το βιβλίο A Guide to Growing Capital από τους Joseph Murphy, Dale Carnegie, Eckhart Tolle, Deepak Chopra, Barbara Sher, Neil Walsh συγγραφέας Στερν Βαλεντίν

Πώς να αρχίσετε να ακολουθείτε τον νόμο της ελάχιστης προσπάθειας: τρεις απαραίτητες ενέργειες Για να αρχίσει να λειτουργεί ο νόμος της ελάχιστης προσπάθειας, πρέπει όχι μόνο να συμμορφωθείτε με τις τρεις προϋποθέσεις που αναφέρονται παραπάνω, αλλά και να εκτελέσετε τρεις ενέργειες. Πρώτη ενέργεια: να αρχίσετε να αποδέχεστε τον κόσμο όπως είναι είναι Αποδοχή

11. Φυσική και Aikido της ελάχιστης δράσης

συγγραφέας Μίντελ Άρνολντ

11. Φυσική και Aikido του μικρότερου εφέ Όταν φυσάει, υπάρχει μόνο άνεμος. Όταν βρέχει, υπάρχει μόνο βροχή. Όταν τα σύννεφα περνούν, ο ήλιος λάμπει μέσα τους. Εάν ανοίξετε τον εαυτό σας στη διορατικότητα, τότε είστε σε ένα με τη διορατικότητα. Και μπορείτε να το χρησιμοποιήσετε πλήρως. Αν ανοίξεις

Η αρχή της ελάχιστης δράσης του Leibniz "Vis Viva"

Από το βιβλίο Γεωψυχολογία στον Σαμανισμό, Φυσική και Ταοϊσμό συγγραφέας Μίντελ Άρνολντ

Η αρχή της ελάχιστης δράσης του Leibniz «Vis Viva» Για την αρχή της ελάχιστης δράσης πρέπει όλοι να ευχαριστήσουμε τον Wilhelm Gottfried Leibniz (1646–1716). Ένας από τους πρώτους «μοντέρνους» φυσικούς και μαθηματικούς, ο Leibniz έζησε την εποχή του Νεύτωνα - μια εποχή που οι επιστήμονες ήταν πιο ανοιχτοί

Aikido - η ενσάρκωση της αρχής της ελάχιστης δράσης

Από το βιβλίο Γεωψυχολογία στον Σαμανισμό, Φυσική και Ταοϊσμό συγγραφέας Μίντελ Άρνολντ

Aikido - η ενσάρκωση της αρχής της ελάχιστης δράσης Η ψυχολογία και η τεχνολογία μας καθοδηγούνται σε μεγάλο βαθμό από μια ιδέα πολύ κοντά στην ιδέα της ελάχιστης δράσης. Προσπαθούμε συνεχώς να κάνουμε τη ζωή μας πιο εύκολη. Οι σημερινοί υπολογιστές δεν είναι αρκετά γρήγοροι. Πρέπει