Ορισμός
Κλιμωτή ποσότητα- μια ποσότητα που μπορεί να χαρακτηριστεί από έναν αριθμό. Για παράδειγμα, μήκος, εμβαδόν, μάζα, θερμοκρασία κ.λπ.
Διάνυσμαονομάζεται το κατευθυνόμενο τμήμα $\overline(A B)$; Το σημείο $A$ είναι η αρχή, το σημείο $B$ είναι το τέλος του διανύσματος (Εικ. 1).
Ένα διάνυσμα συμβολίζεται είτε με δύο κεφαλαία γράμματα - την αρχή και το τέλος του: $\overline(A B)$ είτε με ένα μικρό γράμμα: $\overline(a)$.
Ορισμός
Εάν η αρχή και το τέλος ενός διανύσματος συμπίπτουν, τότε ένα τέτοιο διάνυσμα ονομάζεται μηδέν. Τις περισσότερες φορές, το μηδενικό διάνυσμα συμβολίζεται ως $\overline(0)$.
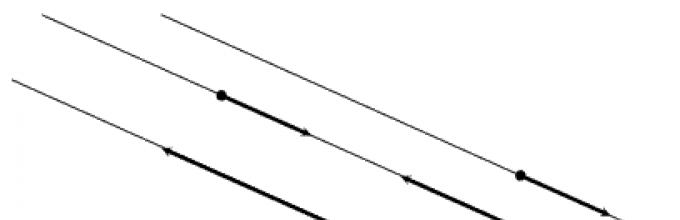
Τα διανύσματα ονομάζονται συγγραμμική, εάν βρίσκονται είτε στην ίδια ευθεία είτε σε παράλληλες ευθείες (Εικ. 2).
Ορισμός
Καλούνται δύο συγγραμμικά διανύσματα $\overline(a)$ και $\overline(b)$ συν-σκηνοθεσία, εάν οι κατευθύνσεις τους συμπίπτουν: $\overline(a) \uparrow \uparrow \overline(b)$ (Εικ. 3, a). Καλούνται δύο συγγραμμικά διανύσματα $\overline(a)$ και $\overline(b)$ αντίθετα κατευθυνόμενη, εάν οι κατευθύνσεις τους είναι αντίθετες: $\overline(a) \uparrow \downarrow \overline(b)$ (Εικ. 3, b).
Ορισμός
Τα διανύσματα ονομάζονται ομοεπίπεδη, εάν είναι παράλληλα στο ίδιο επίπεδο ή βρίσκονται στο ίδιο επίπεδο (Εικ. 4).
Δύο διανύσματα είναι πάντα ομοεπίπεδα.
Ορισμός
Μήκος (ενότητα)διάνυσμα $\overline(A B)$ είναι η απόσταση μεταξύ της αρχής και του τέλους του: $|\overline(A B)|$
Λεπτομερής θεωρία για το μήκος του διανύσματος στον σύνδεσμο.
Το μήκος του μηδενικού διανύσματος είναι μηδέν.
Ορισμός
Ένα διάνυσμα του οποίου το μήκος είναι ίσο με ένα ονομάζεται μονάδα διάνυσμαή ortom.
Τα διανύσματα ονομάζονται ίσος, εάν βρίσκονται σε μία ή παράλληλες γραμμές. οι κατευθύνσεις τους συμπίπτουν και τα μήκη τους είναι ίσα.
Θα υπάρξουν επίσης προβλήματα που θα λύσετε μόνοι σας, στα οποία μπορείτε να δείτε τις απαντήσεις.
Έννοια του φορέα
Πριν μάθετε τα πάντα για τα διανύσματα και τις πράξεις σε αυτά, ετοιμαστείτε να λύσετε ένα απλό πρόβλημα. Υπάρχει ένας φορέας της επιχειρηματικότητάς σας και ένας φορέας των καινοτόμων ικανοτήτων σας. Ο φορέας της επιχειρηματικότητας σε οδηγεί στον στόχο 1 και ο φορέας των καινοτόμων ικανοτήτων σε οδηγεί στον στόχο 2. Οι κανόνες του παιχνιδιού είναι τέτοιοι που δεν μπορείς να κινηθείς κατά τις κατευθύνσεις αυτών των δύο διανυσμάτων ταυτόχρονα και να πετύχεις δύο στόχους ταυτόχρονα. Τα διανύσματα αλληλεπιδρούν ή, μιλώντας σε μαθηματική γλώσσα, εκτελείται κάποια λειτουργία σε διανύσματα. Το αποτέλεσμα αυτής της λειτουργίας είναι το διάνυσμα "Αποτέλεσμα", το οποίο σας οδηγεί στον στόχο 3.
Τώρα πείτε μου: το αποτέλεσμα ποιας πράξης στα διανύσματα "Επιχειρηματικότητα" και "Καινοτόμες ικανότητες" είναι το διάνυσμα "Αποτέλεσμα"; Εάν δεν μπορείτε να το πείτε αμέσως, μην αποθαρρύνεστε. Καθώς προχωράτε σε αυτό το μάθημα, θα είστε σε θέση να απαντήσετε σε αυτήν την ερώτηση.
Όπως είδαμε ήδη παραπάνω, το διάνυσμα προέρχεται απαραίτητα από ένα ορισμένο σημείο ΕΝΑσε ευθεία μέχρι κάποιο σημείο σι. Κατά συνέπεια, κάθε διάνυσμα δεν έχει μόνο μια αριθμητική τιμή - μήκος, αλλά και μια φυσική και γεωμετρική τιμή - κατεύθυνση. Από αυτό προέρχεται ο πρώτος, απλούστερος ορισμός ενός διανύσματος. Άρα, ένα διάνυσμα είναι ένα κατευθυνόμενο τμήμα που προέρχεται από ένα σημείο ΕΝΑμέχρι κάποιο σημείο σι. Ορίζεται ως εξής: .
Και για να ξεκινήσω διάφορα πράξεις με διανύσματα , πρέπει να εξοικειωθούμε με έναν ακόμη ορισμό του διανύσματος.
Ένα διάνυσμα είναι ένας τύπος αναπαράστασης ενός σημείου που πρέπει να επιτευχθεί από κάποιο σημείο εκκίνησης. Για παράδειγμα, ένα τρισδιάστατο διάνυσμα συνήθως γράφεται ως (x, y, z) . Με πολύ απλά λόγια, αυτοί οι αριθμοί σημαίνουν πόσο μακριά πρέπει να περπατήσετε σε τρεις διαφορετικές κατευθύνσεις για να φτάσετε σε ένα σημείο.
Ας δοθεί ένα διάνυσμα. Εν Χ = 3 (το δεξί δείχνει προς τα δεξιά), y = 1 (το αριστερό χέρι δείχνει προς τα εμπρός) z = 5 (κάτω από το σημείο υπάρχει μια σκάλα που οδηγεί προς τα πάνω). Χρησιμοποιώντας αυτά τα δεδομένα, θα βρείτε ένα σημείο περπατώντας 3 μέτρα προς την κατεύθυνση που υποδεικνύεται από το δεξί σας χέρι, μετά 1 μέτρο προς την κατεύθυνση που υποδεικνύεται από το αριστερό σας χέρι και στη συνέχεια μια σκάλα σας περιμένει και, ανεβαίνοντας 5 μέτρα, θα βρείτε επιτέλους τον εαυτό σου στο τελικό σημείο.
Όλοι οι άλλοι όροι είναι διευκρινίσεις της εξήγησης που παρουσιάστηκε παραπάνω, απαραίτητες για διάφορες πράξεις σε διανύσματα, δηλαδή για την επίλυση πρακτικών προβλημάτων. Ας δούμε αυτούς τους πιο αυστηρούς ορισμούς, εστιάζοντας σε τυπικά διανυσματικά προβλήματα.
Φυσικά παραδείγματαδιανυσματικά μεγέθη μπορεί να είναι η μετατόπιση ενός υλικού σημείου που κινείται στο χώρο, η ταχύτητα και η επιτάχυνση αυτού του σημείου, καθώς και η δύναμη που ασκείται σε αυτό.
Γεωμετρικό διάνυσμαπαρουσιάζονται σε δισδιάστατο και τρισδιάστατο χώρο στη μορφή κατευθυντικό τμήμα. Αυτό είναι ένα τμήμα που έχει αρχή και τέλος.
Αν ΕΝΑ- η αρχή του διανύσματος, και σι- το τέλος του, τότε το διάνυσμα συμβολίζεται με το σύμβολο ή ένα πεζό γράμμα . Στο σχήμα, το τέλος του διανύσματος υποδεικνύεται με ένα βέλος (Εικ. 1)
Μήκος(ή μονάδα μέτρησης) ενός γεωμετρικού διανύσματος είναι το μήκος του τμήματος που το δημιουργεί
Τα δύο διανύσματα ονομάζονται ίσος , αν μπορούν να συνδυαστούν (αν οι κατευθύνσεις συμπίπτουν) με παράλληλη μεταφορά, δηλ. αν είναι παράλληλα, κατευθύνονται προς την ίδια κατεύθυνση και έχουν ίσα μήκη.
Στη φυσική θεωρείται συχνά καρφιτσωμένα διανύσματα, καθορίζεται από το σημείο εφαρμογής, το μήκος και την κατεύθυνση. Εάν το σημείο εφαρμογής του διανύσματος δεν έχει σημασία, τότε μπορεί να μεταφερθεί, διατηρώντας το μήκος και την κατεύθυνσή του, σε οποιοδήποτε σημείο του χώρου. Στην περίπτωση αυτή καλείται το διάνυσμα Ελεύθερος. Θα συμφωνήσουμε να εξετάσουμε μόνο ελεύθερα διανύσματα.
Γραμμικές πράξεις σε γεωμετρικά διανύσματα
Πολλαπλασιάζοντας ένα διάνυσμα με έναν αριθμό
Προϊόν ενός φορέα ανά αριθμόείναι ένα διάνυσμα που λαμβάνεται από ένα διάνυσμα με τάνυση (at ) ή συμπίεση (at ) κατά έναν παράγοντα, και η κατεύθυνση του διανύσματος παραμένει η ίδια αν , και αλλάζει στο αντίθετο εάν . (Εικ. 2)
Από τον ορισμό προκύπτει ότι τα διανύσματα και = βρίσκονται πάντα σε μία ή παράλληλες ευθείες. Τέτοια διανύσματα ονομάζονται συγγραμμική. (Μπορούμε επίσης να πούμε ότι αυτά τα διανύσματα είναι παράλληλα, αλλά στη διανυσματική άλγεβρα συνηθίζεται να λέμε "συγγραμμικό.") Το αντίστροφο ισχύει επίσης: εάν τα διανύσματα είναι συγγραμμικά, τότε σχετίζονται με τη σχέση
Κατά συνέπεια, η ισότητα (1) εκφράζει την συνθήκη συγγραμμικότητας δύο διανυσμάτων.
Πρόσθεση και αφαίρεση διανυσμάτων
Όταν προσθέτετε διανύσματα πρέπει να το γνωρίζετε ποσόδιανύσματα και ονομάζεται διάνυσμα, η αρχή του οποίου συμπίπτει με την αρχή του διανύσματος και το τέλος - με το τέλος του διανύσματος, υπό την προϋπόθεση ότι η αρχή του διανύσματος συνδέεται με το τέλος του διανύσματος. (Εικ. 3)
Αυτός ο ορισμός μπορεί να κατανεμηθεί σε οποιονδήποτε πεπερασμένο αριθμό διανυσμάτων. Αφήστε τα να δοθούν στο διάστημα nελεύθερα διανύσματα. Όταν προσθέτουμε πολλά διανύσματα, το άθροισμά τους λαμβάνεται ως το διάνυσμα κλεισίματος, η αρχή του οποίου συμπίπτει με την αρχή του πρώτου διανύσματος και το τέλος με το τέλος του τελευταίου διανύσματος. Δηλαδή, εάν επισυνάψετε την αρχή του διανύσματος στο τέλος του διανύσματος και την αρχή του διανύσματος στο τέλος του διανύσματος κ.λπ. και, τέλος, στο τέλος του διανύσματος - η αρχή του διανύσματος, τότε το άθροισμα αυτών των διανυσμάτων είναι το διάνυσμα κλεισίματος 
, η αρχή του οποίου συμπίπτει με την αρχή του πρώτου διανύσματος και το τέλος - με το τέλος του τελευταίου διανύσματος. (Εικ. 4)
Οι όροι ονομάζονται συστατικά του διανύσματος και ο διατυπωμένος κανόνας είναι κανόνας πολυγώνου. Αυτό το πολύγωνο μπορεί να μην είναι επίπεδο.
Όταν ένα διάνυσμα πολλαπλασιάζεται με τον αριθμό -1, προκύπτει το αντίθετο διάνυσμα. Τα διανύσματα και έχουν τα ίδια μήκη και αντίθετες κατευθύνσεις. Το άθροισμά τους δίνει μηδενικό διάνυσμα, του οποίου το μήκος είναι μηδέν. Η κατεύθυνση του μηδενικού διανύσματος δεν έχει καθοριστεί.
Στη διανυσματική άλγεβρα, δεν υπάρχει ανάγκη να εξεταστεί χωριστά η λειτουργία αφαίρεσης: η αφαίρεση ενός διανύσματος από ένα διάνυσμα σημαίνει προσθήκη του αντίθετου διανύσματος στο διάνυσμα, δηλ. 
Παράδειγμα 1.Απλοποιήστε την έκφραση:
.
,
Δηλαδή, τα διανύσματα μπορούν να προστεθούν και να πολλαπλασιαστούν με αριθμούς με τον ίδιο τρόπο όπως τα πολυώνυμα (ιδιαίτερα, επίσης προβλήματα απλοποίησης παραστάσεων). Τυπικά, η ανάγκη να απλοποιηθούν γραμμικά παρόμοιες εκφράσεις με διανύσματα προκύπτει πριν από τον υπολογισμό των γινομένων των διανυσμάτων.
Παράδειγμα 2.Διανύσματα και χρησιμεύουν ως διαγώνιοι του παραλληλογράμμου ABCD (Εικ. 4α). Εκφράστε μέσω και τα διανύσματα , , και , που είναι οι πλευρές αυτού του παραλληλογράμμου.
Λύση. Το σημείο τομής των διαγωνίων ενός παραλληλογράμμου διχοτομεί κάθε διαγώνιο. Βρίσκουμε τα μήκη των διανυσμάτων που απαιτούνται στη δήλωση του προβλήματος είτε ως τα μισά αθροίσματα των διανυσμάτων που σχηματίζουν τρίγωνο με τα απαιτούμενα είτε ως το ήμισυ των διαφορών (ανάλογα με την κατεύθυνση του διανύσματος που χρησιμεύει ως διαγώνιος) ή όπως και στην τελευταία περίπτωση, το ήμισυ του ποσού που λαμβάνεται με πρόσημο μείον. Το αποτέλεσμα είναι τα διανύσματα που απαιτούνται στη δήλωση προβλήματος:
Υπάρχει κάθε λόγος να πιστεύουμε ότι τώρα έχετε απαντήσει σωστά στην ερώτηση σχετικά με τα διανύσματα «Επιχειρηματικότητα» και «Καινοτόμες ικανότητες» στην αρχή αυτού του μαθήματος. Σωστή απάντηση: εκτελείται μια πράξη πρόσθεσης σε αυτά τα διανύσματα.
Λύστε μόνοι σας διανυσματικά προβλήματα και μετά δείτε τις λύσεις
Πώς να βρείτε το μήκος του αθροίσματος των διανυσμάτων;
Αυτό το πρόβλημα κατέχει ιδιαίτερη θέση στις πράξεις με διανύσματα, καθώς περιλαμβάνει τη χρήση τριγωνομετρικών ιδιοτήτων. Ας υποθέσουμε ότι συναντάτε μια εργασία όπως η παρακάτω:
Δίνονται τα διανυσματικά μήκη. 
και το μήκος του αθροίσματος αυτών των διανυσμάτων. Βρείτε το μήκος της διαφοράς μεταξύ αυτών των διανυσμάτων.
Λύσεις σε αυτό και άλλα παρόμοια προβλήματα και εξηγήσεις για τον τρόπο επίλυσής τους υπάρχουν στο μάθημα " Διάνυσμα πρόσθεση: μήκος του αθροίσματος των διανυσμάτων και του συνημιτόνου ".
Και μπορείτε να ελέγξετε τη λύση σε τέτοια προβλήματα στο Ηλεκτρονική αριθμομηχανή "Άγνωστη πλευρά ενός τριγώνου (διανυσματική πρόσθεση και θεώρημα συνημιτόνου)" .
Πού βρίσκονται τα γινόμενα των διανυσμάτων;
Τα προϊόντα διανύσματος-διανύσματος δεν είναι γραμμικές πράξεις και εξετάζονται χωριστά. Και έχουμε μαθήματα «Βαθμιακό γινόμενο διανυσμάτων» και «Διανυσματικά και μικτά γινόμενα διανυσμάτων».
Προβολή ενός διανύσματος σε έναν άξονα
Η προβολή ενός διανύσματος σε έναν άξονα είναι ίση με το γινόμενο του μήκους του προβαλλόμενου διανύσματος και του συνημιτόνου της γωνίας μεταξύ του διανύσματος και του άξονα:
Ως γνωστόν, η προβολή ενός σημείου ΕΝΑστην ευθεία (επίπεδο) είναι η βάση της καθέτου που έπεσε από αυτό το σημείο στην ευθεία (επίπεδο).
Έστω ένα αυθαίρετο διάνυσμα (Εικ. 5) και και οι προβολές της προέλευσής του (σημεία ΕΝΑ) και τέλος (πόντους σι) ανά άξονα μεγάλο. (Για να κατασκευάσετε μια προβολή ενός σημείου ΕΝΑ) σχεδιάστε μια ευθεία γραμμή μέσα από το σημείο ΕΝΑεπίπεδο κάθετο σε ευθεία γραμμή. Η τομή της γραμμής και του επιπέδου θα καθορίσει την απαιτούμενη προβολή.
Διάνυσμα συστατικό στον άξονα lονομάζεται ένα τέτοιο διάνυσμα που βρίσκεται σε αυτόν τον άξονα, η αρχή του οποίου συμπίπτει με την προβολή της αρχής και το τέλος με την προβολή του τέλους του διανύσματος.
Προβολή του διανύσματος στον άξονα μεγάλοκαλούμενος αριθμός
,
ίσο με το μήκος του διανύσματος συνιστωσών σε αυτόν τον άξονα, λαμβανόμενο με το σύμβολο συν εάν η κατεύθυνση των στοιχείων συμπίπτει με την κατεύθυνση του άξονα μεγάλο, και με πρόσημο μείον εάν αυτές οι κατευθύνσεις είναι αντίθετες.
Βασικές ιδιότητες των διανυσματικών προβολών σε έναν άξονα:
1. Οι προβολές ίσων διανυσμάτων στον ίδιο άξονα είναι ίσες μεταξύ τους.
2. Όταν ένα διάνυσμα πολλαπλασιάζεται με έναν αριθμό, η προβολή του πολλαπλασιάζεται με τον ίδιο αριθμό.
3. Η προβολή του αθροίσματος των διανυσμάτων σε οποιονδήποτε άξονα είναι ίση με το άθροισμα των προβολών των αθροίσεων των διανυσμάτων στον ίδιο άξονα.
4. Η προβολή του διανύσματος στον άξονα είναι ίση με το γινόμενο του μήκους του προβαλλόμενου διανύσματος και του συνημιτόνου της γωνίας μεταξύ του διανύσματος και του άξονα:
.
Λύση. Ας προβάλουμε διανύσματα στον άξονα μεγάλοόπως ορίζεται στο παραπάνω θεωρητικό υπόβαθρο. Από το Σχ. 5α είναι προφανές ότι η προβολή του αθροίσματος των διανυσμάτων είναι ίση με το άθροισμα των προβολών των διανυσμάτων. Υπολογίζουμε αυτές τις προβολές:
Βρίσκουμε την τελική προβολή του αθροίσματος των διανυσμάτων:
Σχέση μεταξύ ενός διανύσματος και ενός ορθογώνιου καρτεσιανού συστήματος συντεταγμένων στο χώρο
Γνωριμία ορθογώνιο καρτεσιανό σύστημα συντεταγμένων στο χώρο έλαβε χώρα στο αντίστοιχο μάθημα, καλό είναι να το ανοίξετε σε νέο παράθυρο.
Σε ένα διατεταγμένο σύστημα αξόνων συντεταγμένων 0xyzάξονας Βόδιπου ονομάζεται άξονας x, άξονας 0 ε – άξονας y, και άξονα 0z – άξονας εφαρμογή.
Με ένα αυθαίρετο σημείο Μδιάνυσμα σύνδεσης χώρου
που ονομάζεται διάνυσμα ακτίναςσημεία Μκαι να το προβάλετε σε κάθε έναν από τους άξονες συντεταγμένων. Ας υποδηλώσουμε τα μεγέθη των αντίστοιχων προβολών:
Αριθμοί x, y, zλέγονται συντεταγμένες του σημείου Μ, αντίστοιχα τετμημένη, τεταγμένηΚαι αίτηση, και γράφονται ως διατεταγμένο σημείο αριθμών: M(x;y;z)(Εικ. 6).
Ένα διάνυσμα μοναδιαίου μήκους του οποίου η διεύθυνση συμπίπτει με την κατεύθυνση του άξονα ονομάζεται μονάδα διάνυσμα(ή ortom) τσεκούρια. Ας υποδηλώσουμε με
Αντίστοιχα, τα μοναδιαία διανύσματα των αξόνων συντεταγμένων Βόδι, Oy, Οζ
Θεώρημα.Οποιοδήποτε διάνυσμα μπορεί να επεκταθεί σε μοναδιαία διανύσματα αξόνων συντεταγμένων:
(2)
Ισότητα (2) ονομάζεται η επέκταση του διανύσματος κατά μήκος των αξόνων συντεταγμένων. Οι συντελεστές αυτής της επέκτασης είναι οι προβολές του διανύσματος στους άξονες συντεταγμένων. Έτσι, οι συντελεστές διαστολής (2) του διανύσματος κατά μήκος των αξόνων συντεταγμένων είναι οι συντεταγμένες του διανύσματος.
Μετά την επιλογή ενός συγκεκριμένου συστήματος συντεταγμένων στο χώρο, το διάνυσμα και η τριπλέτα των συντεταγμένων του καθορίζουν μοναδικά το ένα το άλλο, έτσι το διάνυσμα μπορεί να γραφτεί με τη μορφή
Οι αναπαραστάσεις του διανύσματος στη μορφή (2) και (3) είναι πανομοιότυπες.
Συνθήκη για συγγραμμικότητα διανυσμάτων σε συντεταγμένες
Όπως έχουμε ήδη σημειώσει, τα διανύσματα ονομάζονται συγγραμμικά εάν σχετίζονται με τη σχέση
Αφήστε τα διανύσματα να δοθούν 
. Αυτά τα διανύσματα είναι συγγραμμικά εάν οι συντεταγμένες των διανυσμάτων σχετίζονται με τη σχέση
,
δηλαδή οι συντεταγμένες των διανυσμάτων είναι ανάλογες.
Παράδειγμα 6.Δίνονται διανύσματα 
. Είναι αυτά τα διανύσματα συγγραμμικά;
Λύση. Ας μάθουμε τη σχέση μεταξύ των συντεταγμένων αυτών των διανυσμάτων:
.
Οι συντεταγμένες των διανυσμάτων είναι ανάλογες, επομένως, τα διανύσματα είναι συγγραμμικά ή, το ίδιο, παράλληλα.
Διάνυσμα συνημίτονα μήκους και κατεύθυνσης
Λόγω της αμοιβαίας καθετότητας των αξόνων συντεταγμένων, το μήκος του διανύσματος
ίσο με το μήκος της διαγωνίου ενός ορθογώνιου παραλληλεπίπεδου χτισμένου σε διανύσματα
και εκφράζεται με την ισότητα
(4)
Ένα διάνυσμα ορίζεται πλήρως καθορίζοντας δύο σημεία (αρχή και τέλος), έτσι οι συντεταγμένες του διανύσματος μπορούν να εκφραστούν ως προς τις συντεταγμένες αυτών των σημείων.
Έστω, σε ένα δεδομένο σύστημα συντεταγμένων, η αρχή του διανύσματος είναι στο σημείο
και το τέλος είναι στο σημείο
Από την ισότητα
Ακολουθεί αυτό
ή σε συντεταγμένη μορφή
Ως εκ τούτου, οι διανυσματικές συντεταγμένες είναι ίσες με τις διαφορές μεταξύ των ίδιων συντεταγμένων του τέλους και της αρχής του διανύσματος . Ο τύπος (4) σε αυτήν την περίπτωση θα λάβει τη μορφή
Καθορίζεται η κατεύθυνση του διανύσματος συνημίτονα κατεύθυνσης . Αυτά είναι τα συνημίτονα των γωνιών που κάνει το διάνυσμα με τους άξονες Βόδι, OyΚαι Οζ. Ας υποδηλώσουμε αυτές τις γωνίες ανάλογα α , β Και γ . Στη συνέχεια, τα συνημίτονα αυτών των γωνιών μπορούν να βρεθούν χρησιμοποιώντας τους τύπους
Τα συνημίτονα κατεύθυνσης ενός διανύσματος είναι επίσης οι συντεταγμένες του διανύσματος αυτού του διανύσματος και επομένως το διάνυσμα του διανύσματος
.
Λαμβάνοντας υπόψη ότι το μήκος του μοναδιαίου διανύσματος είναι ίσο με μία μονάδα, δηλαδή
,
λαμβάνουμε την ακόλουθη ισότητα για τα συνημίτονα κατεύθυνσης:
Παράδειγμα 7.Βρείτε το μήκος του διανύσματος Χ = (3; 0; 4).
Λύση. Το μήκος του διανύσματος είναι
Παράδειγμα 8.Βαθμοί που δίνονται:
Μάθετε αν το τρίγωνο που κατασκευάζεται σε αυτά τα σημεία είναι ισοσκελές.
Λύση. Χρησιμοποιώντας τον τύπο του διανυσματικού μήκους (6), βρίσκουμε τα μήκη των πλευρών και προσδιορίζουμε αν υπάρχουν δύο ίσες μεταξύ τους:
Έχουν βρεθεί δύο ίσες πλευρές, επομένως δεν χρειάζεται να αναζητήσετε το μήκος της τρίτης πλευράς και το δεδομένο τρίγωνο είναι ισοσκελές.
Παράδειγμα 9.Να βρείτε το μήκος του διανύσματος και τα συνημίτονα κατεύθυνσής του αν 
.
Λύση. Δίνονται οι συντεταγμένες του διανύσματος:
.
Το μήκος του διανύσματος είναι ίσο με την τετραγωνική ρίζα του αθροίσματος των τετραγώνων των συντεταγμένων του διανύσματος:
.
Εύρεση συνημιτόνων κατεύθυνσης:
Λύστε μόνοι σας το διανυσματικό πρόβλημα και μετά δείτε τη λύση
Πράξεις σε διανύσματα που δίνονται σε μορφή συντεταγμένων
Έστω δύο διανύσματα και δίνονται, που ορίζονται από τις προβολές τους:
Ας υποδείξουμε ενέργειες σε αυτά τα διανύσματα.
Το μήκος του διανύσματος a → θα συμβολίζεται με ένα → . Αυτός ο συμβολισμός είναι παρόμοιος με τον συντελεστή ενός αριθμού, επομένως το μήκος ενός διανύσματος ονομάζεται επίσης συντελεστής ενός διανύσματος.
Για να βρείτε το μήκος ενός διανύσματος σε ένα επίπεδο από τις συντεταγμένες του, είναι απαραίτητο να εξετάσουμε ένα ορθογώνιο καρτεσιανό σύστημα συντεταγμένων O x y. Έστω κάποιο διάνυσμα a → με συντεταγμένες x να καθοριστεί σε αυτό. αι. Ας εισαγάγουμε έναν τύπο για την εύρεση του μήκους (μέτρο) του διανύσματος a → μέσω των συντεταγμένων a x και a y.
Ας σχεδιάσουμε το διάνυσμα O A → = a → από την αρχή. Ας ορίσουμε τις αντίστοιχες προβολές του σημείου Α στους άξονες συντεταγμένων ως A x και A y. Τώρα θεωρήστε ένα ορθογώνιο O A x A A y με διαγώνιο O A .
Από το Πυθαγόρειο θεώρημα ακολουθεί η ισότητα O A 2 = O A x 2 + O A y 2 , από όπου O A = O A x 2 + O A y 2 . Από τον ήδη γνωστό ορισμό των διανυσματικών συντεταγμένων σε ένα ορθογώνιο καρτεσιανό σύστημα συντεταγμένων, λαμβάνουμε ότι O A x 2 = a x 2 και O A y 2 = a y 2 , και κατά κατασκευή, το μήκος του O A είναι ίσο με το μήκος του διανύσματος O A → , που σημαίνει O A → = O A x 2 + O A y 2.
Από αυτό προκύπτει ότι τύπος για την εύρεση του μήκους ενός διανύσματος a → = a x ; a y έχει την αντίστοιχη μορφή: a → = a x 2 + a y 2 .
Εάν το διάνυσμα a → δίνεται με τη μορφή επέκτασης σε διανύσματα συντεταγμένων a → = a x i → + a y j →, τότε το μήκος του μπορεί να υπολογιστεί χρησιμοποιώντας τον ίδιο τύπο a → = a x 2 + a y 2, στην περίπτωση αυτή οι συντελεστές a x και a y είναι οι συντεταγμένες του διανύσματος a → σε ένα δεδομένο σύστημα συντεταγμένων.
Παράδειγμα 1
Υπολογίστε το μήκος του διανύσματος a → = 7 ; e, που καθορίζεται σε ένα ορθογώνιο σύστημα συντεταγμένων.
Λύση
Για να βρούμε το μήκος ενός διανύσματος, θα χρησιμοποιήσουμε τον τύπο για την εύρεση του μήκους ενός διανύσματος από τις συντεταγμένες a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e
Απάντηση: a → = 49 + e.
Τύπος για την εύρεση του μήκους ενός διανύσματος a → = a x ; a y; Το a z από τις συντεταγμένες του στο καρτεσιανό σύστημα συντεταγμένων Oxyz στο διάστημα, προέρχεται παρόμοια με τον τύπο για την περίπτωση σε ένα επίπεδο (βλ. παρακάτω σχήμα)
Σε αυτήν την περίπτωση, O A 2 = O A x 2 + O A y 2 + O A z 2 (καθώς το OA είναι η διαγώνιος ενός ορθογώνιου παραλληλεπιπέδου), επομένως O A = O A x 2 + O A y 2 + O A z 2 . Από τον ορισμό των διανυσματικών συντεταγμένων μπορούμε να γράψουμε τις ακόλουθες ισότητες O A x = a x ; O A y = a y ; O A z = a z ; , και το μήκος OA είναι ίσο με το μήκος του διανύσματος που αναζητούμε, επομένως, O A → = O A x 2 + O A y 2 + O A z 2 .
Από αυτό προκύπτει ότι το μήκος του διανύσματος a → = a x ; a y; a z ισούται με a → = a x 2 + a y 2 + a z 2 .
Παράδειγμα 2
Υπολογίστε το μήκος του διανύσματος a → = 4 · i → - 3 · j → + 5 · k → , όπου i → , j → , k → είναι τα μοναδιαία διανύσματα του ορθογώνιου συστήματος συντεταγμένων.
Λύση
Δίνεται η αποσύνθεση του διανύσματος a → = 4 · i → - 3 · j → + 5 · k →, οι συντεταγμένες του είναι a → = 4, - 3, 5. Χρησιμοποιώντας τον παραπάνω τύπο παίρνουμε a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2.
Απάντηση: a → = 5 2 .
Μήκος ενός διανύσματος μέσω των συντεταγμένων των σημείων έναρξης και τέλους του
Προέκυψαν τύποι παραπάνω που σας επιτρέπουν να βρείτε το μήκος ενός διανύσματος από τις συντεταγμένες του. Εξετάσαμε περιπτώσεις σε επίπεδο και σε τρισδιάστατο χώρο. Ας τις χρησιμοποιήσουμε για να βρούμε τις συντεταγμένες ενός διανύσματος από τις συντεταγμένες των σημείων έναρξης και τέλους του.
Δίνονται λοιπόν σημεία με δεδομένες συντεταγμένες A (a x ; a y) και B (b x ; b y), επομένως το διάνυσμα A B → έχει συντεταγμένες (b x - a x; b y - a y) που σημαίνει ότι το μήκος του μπορεί να προσδιοριστεί από τον τύπο: A B → = ( b x - a x) 2 + (b y - a y) 2
Και αν σημεία με δεδομένες συντεταγμένες A (a x ; a y ; a z) και B (b x ; b y ; b z) δίνονται σε τρισδιάστατο χώρο, τότε το μήκος του διανύσματος A B → μπορεί να υπολογιστεί χρησιμοποιώντας τον τύπο
A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2
Παράδειγμα 3
Να βρείτε το μήκος του διανύσματος A B → αν στο ορθογώνιο σύστημα συντεταγμένων A 1, 3, B - 3, 1.
Λύση
Χρησιμοποιώντας τον τύπο για την εύρεση του μήκους ενός διανύσματος από τις συντεταγμένες των σημείων έναρξης και τέλους στο επίπεδο, λαμβάνουμε A B → = (b x - a x) 2 + (b y - a y) 2: A B → = (- 3 - 1 ) 2 + (1 - 3) 2 = 20 - 2 3 .
Η δεύτερη λύση περιλαμβάνει την εφαρμογή αυτών των τύπων με τη σειρά: A B → = (- 3 - 1 ; 1 - 3) = (- 4 ; 1 - 3) ; A B → = (- 4) 2 + (1 - 3) 2 = 20 - 2 3 . -
Απάντηση: A B → = 20 - 2 3 .
Παράδειγμα 4
Προσδιορίστε σε ποιες τιμές το μήκος του διανύσματος A B → είναι ίσο με 30 εάν A (0, 1, 2). Β (5 , 2 , λ 2) .
Λύση
Αρχικά, ας γράψουμε το μήκος του διανύσματος A B → χρησιμοποιώντας τον τύπο: A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 = (5 - 0) 2 + (2 - 1) 2 + (λ 2 - 2) 2 = 26 + (λ 2 - 2) 2
Στη συνέχεια, εξισώνουμε την παράσταση που προκύπτει με 30, από εδώ βρίσκουμε το απαιτούμενο λ:
26 + (λ 2 - 2) 2 = 30 26 + (λ 2 - 2) 2 = 30 (λ 2 - 2) 2 = 4 λ 2 - 2 = 2 και λ 2 - 2 = - 2 λ 1 = - 2 , λ 2 = 2, λ 3 = 0.
Απάντηση: λ 1 = - 2, λ 2 = 2, λ 3 = 0.
Εύρεση του μήκους ενός διανύσματος χρησιμοποιώντας το θεώρημα συνημιτόνου
Δυστυχώς, στα προβλήματα οι συντεταγμένες του διανύσματος δεν είναι πάντα γνωστές, επομένως θα εξετάσουμε άλλους τρόπους για να βρούμε το μήκος του διανύσματος.
Αφήστε τα μήκη δύο διανυσμάτων A B → , A C → και τη γωνία μεταξύ τους (ή το συνημίτονο της γωνίας) και πρέπει να βρείτε το μήκος του διανύσματος B C → ή C B → . Σε αυτήν την περίπτωση, θα πρέπει να χρησιμοποιήσετε το θεώρημα συνημιτόνου στο τρίγωνο △ A B C και να υπολογίσετε το μήκος της πλευράς B C, το οποίο είναι ίσο με το επιθυμητό μήκος του διανύσματος.
Ας εξετάσουμε αυτήν την περίπτωση χρησιμοποιώντας το ακόλουθο παράδειγμα.
Παράδειγμα 5
Τα μήκη των διανυσμάτων A B → και A C → είναι 3 και 7, αντίστοιχα, και η μεταξύ τους γωνία είναι π 3. Να υπολογίσετε το μήκος του διανύσματος B C → .
Λύση
Το μήκος του διανύσματος B C → στην περίπτωση αυτή είναι ίσο με το μήκος της πλευράς B C του τριγώνου △ A B C . Τα μήκη των πλευρών Α Β και Α Γ του τριγώνου είναι γνωστά από την συνθήκη (είναι ίσα με τα μήκη των αντίστοιχων διανυσμάτων), η μεταξύ τους γωνία είναι επίσης γνωστή, οπότε μπορούμε να χρησιμοποιήσουμε το θεώρημα συνημιτόνου: B C 2 = A B 2 + A C 2 - 2 A B A C cos ∠ (A B, → A C →) = 3 2 + 7 2 - 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Έτσι, B C → = 37 .
Απάντηση: B C → = 37 .
Έτσι, για να βρείτε το μήκος ενός διανύσματος από συντεταγμένες, υπάρχουν οι ακόλουθοι τύποι a → = a x 2 + a y 2 ή a → = a x 2 + a y 2 + a z 2 , από τις συντεταγμένες των σημείων έναρξης και τέλους του διανύσματος A B → = (b x - a x) 2 + ( b y - a y) 2 ή A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2, σε ορισμένες περιπτώσεις θα πρέπει να χρησιμοποιείται το θεώρημα συνημιτόνου .
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
Oxy
ΣΧΕΤΙΚΑ ΜΕ ΕΝΑ ΟΑ.
, που 
ΟΑ 
.
Ετσι, 
.
Ας δούμε ένα παράδειγμα.
Παράδειγμα.
Λύση.
:
Απάντηση:
Oxyzστο διάστημα.
ΕΝΑ ΟΑθα είναι διαγώνιος.
Σε αυτή την περίπτωση (από ΟΑ 
ΟΑ 
.
Ετσι, διανυσματικό μήκος 
.
Παράδειγμα.
Υπολογίστε το μήκος του διανύσματος 
Λύση.
, ως εκ τούτου, 
Απάντηση:
Ευθεία γραμμή σε ένα αεροπλάνο
Γενική εξίσωση
Ax + By + C ( > 0).
Διάνυσμα = (Α; Β)είναι ένα κανονικό διάνυσμα.
Σε διανυσματική μορφή: + C = 0, όπου είναι το διάνυσμα ακτίνας ενός αυθαίρετου σημείου σε μια ευθεία (Εικ. 4.11).
Ειδικές περιπτώσεις:
1) Κατά + C = 0- ευθεία παράλληλη προς τον άξονα Βόδι;
2) Ax + C = 0- ευθεία παράλληλη προς τον άξονα Oy;
3) Ax + By = 0- η ευθεία διέρχεται από την αρχή.
4) y = 0- άξονας Βόδι;
5) x = 0- άξονας Oy.
Εξίσωση ευθείας σε τμήματα
Οπου α, β- οι τιμές των τμημάτων που αποκόπτονται από την ευθεία στους άξονες συντεταγμένων.
Κανονική εξίσωση μιας γραμμής(Εικ. 4.11)
όπου είναι η γωνία που σχηματίζεται κάθετη προς την ευθεία και τον άξονα Βόδι; Π- την απόσταση από την αρχή έως την ευθεία.
Αναγωγή της γενικής εξίσωσης μιας γραμμής σε κανονική μορφή:
Εδώ είναι ο κανονικοποιημένος παράγοντας της γραμμής. το πρόσημο επιλέγεται απέναντι από το σημάδι ντο, εάν και αυθαίρετα, εάν C=0.
Εύρεση του μήκους ενός διανύσματος από συντεταγμένες.
Θα συμβολίσουμε το μήκος του διανύσματος με . Λόγω αυτού του συμβολισμού, το μήκος ενός διανύσματος ονομάζεται συχνά μέτρο του διανύσματος.
Ας ξεκινήσουμε βρίσκοντας το μήκος ενός διανύσματος σε ένα επίπεδο χρησιμοποιώντας συντεταγμένες.
Ας εισάγουμε ένα ορθογώνιο καρτεσιανό σύστημα συντεταγμένων στο επίπεδο Oxy. Έστω ένα διάνυσμα να καθορίζεται σε αυτό και να έχει συντεταγμένες . Λαμβάνουμε έναν τύπο που μας επιτρέπει να βρούμε το μήκος ενός διανύσματος μέσω των συντεταγμένων και .
Ας αναβάλουμε από την αρχή των συντεταγμένων (από το σημείο ΣΧΕΤΙΚΑ ΜΕ) διάνυσμα . Ας υποδηλώσουμε τις προβολές του σημείου ΕΝΑστους άξονες συντεταγμένων ως και αντίστοιχα και θεωρήστε ένα ορθογώνιο με διαγώνιο ΟΑ.
Δυνάμει του Πυθαγόρειου θεωρήματος, η ισότητα , που . Από τον ορισμό των διανυσματικών συντεταγμένων σε ένα ορθογώνιο σύστημα συντεταγμένων, μπορούμε να δηλώσουμε ότι και , και κατασκευάζοντας το μήκος ΟΑίσο με το μήκος του διανύσματος, επομένως, .
Ετσι, τύπος για την εύρεση του μήκους ενός διανύσματοςσύμφωνα με τις συντεταγμένες του στο επίπεδο έχει τη μορφή .
Αν το διάνυσμα παριστάνεται ως αποσύνθεση σε διανύσματα συντεταγμένων , τότε το μήκος του υπολογίζεται με τον ίδιο τύπο , αφού στην περίπτωση αυτή οι συντελεστές και είναι οι συντεταγμένες του διανύσματος σε ένα δεδομένο σύστημα συντεταγμένων.
Ας δούμε ένα παράδειγμα.
Παράδειγμα.
Βρείτε το μήκος του διανύσματος που δίνεται στο καρτεσιανό σύστημα συντεταγμένων.
Λύση.
Εφαρμόζουμε αμέσως τον τύπο για να βρούμε το μήκος του διανύσματος από τις συντεταγμένες :
Απάντηση:
Τώρα παίρνουμε τον τύπο για την εύρεση του μήκους του διανύσματος από τις συντεταγμένες του σε ένα ορθογώνιο σύστημα συντεταγμένων Oxyzστο διάστημα.
Ας σχεδιάσουμε το διάνυσμα από την αρχή και δηλώνουμε τις προβολές του σημείου ΕΝΑστους άξονες συντεταγμένων ως και . Στη συνέχεια μπορούμε να κατασκευάσουμε ένα ορθογώνιο παραλληλεπίπεδο στις πλευρές, στο οποίο ΟΑθα είναι διαγώνιος.
Σε αυτή την περίπτωση (από ΟΑ– διαγώνιος ορθογώνιου παραλληλεπιπέδου), από όπου . Ο προσδιορισμός των συντεταγμένων ενός διανύσματος μας επιτρέπει να γράψουμε ισότητες και μήκος ΟΑίσο με το επιθυμητό διανυσματικό μήκος, επομένως, .
Ετσι, διανυσματικό μήκος στο διάστημα ισούται με την τετραγωνική ρίζα του αθροίσματος των τετραγώνων των συντεταγμένων του, δηλαδή, βρίσκεται από τον τύπο .
Παράδειγμα.
Υπολογίστε το μήκος του διανύσματος , όπου είναι τα μοναδιαία διανύσματα του ορθογώνιου συστήματος συντεταγμένων.
Λύση.
Μας δίνεται μια διανυσματική αποσύνθεση σε διανύσματα συντεταγμένων της μορφής , ως εκ τούτου, . Στη συνέχεια, χρησιμοποιώντας τον τύπο για την εύρεση του μήκους ενός διανύσματος από συντεταγμένες, έχουμε .
Πριν προχωρήσουμε στο θέμα του άρθρου, ας θυμηθούμε τις βασικές έννοιες.
Ορισμός 1
Διάνυσμα– ευθύγραμμο τμήμα που χαρακτηρίζεται από αριθμητική τιμή και κατεύθυνση. Ένα διάνυσμα συμβολίζεται με ένα πεζό λατινικό γράμμα με ένα βέλος στην κορυφή. Εάν υπάρχουν συγκεκριμένα οριακά σημεία, ο προσδιορισμός του διανύσματος μοιάζει με δύο κεφαλαία λατινικά γράμματα (που επισημαίνουν τα όρια του διανύσματος) επίσης με ένα βέλος στην κορυφή.
Ορισμός 2
Μηδενικό διάνυσμα– οποιοδήποτε σημείο στο επίπεδο, που ορίζεται ως μηδέν με ένα βέλος στην κορυφή.
Ορισμός 3
Διάνυσμα μήκος– τιμή ίση ή μεγαλύτερη από το μηδέν που καθορίζει το μήκος του τμήματος που αποτελεί το διάνυσμα.
Ορισμός 4
Συγγραμμικά διανύσματα– ξαπλωμένος σε μία γραμμή ή σε παράλληλες γραμμές. Τα διανύσματα που δεν πληρούν αυτή την προϋπόθεση ονομάζονται μη συγγραμμικά.
Ορισμός 5Εισαγωγή: διανύσματα α →Και β →. Για να εκτελέσετε μια λειτουργία πρόσθεσης σε αυτά, είναι απαραίτητο να σχεδιάσετε ένα διάνυσμα από ένα αυθαίρετο απροσδιόριστο σημείο Α Β →, ίσο με το διάνυσμα α →; από το προκύπτον σημείο απροσδιόριστο – διάνυσμα B C →, ίσο με το διάνυσμα β →. Συνδέοντας τα ακαθόριστα σημεία και το C, παίρνουμε ένα τμήμα (διάνυσμα) A C →, που θα είναι το άθροισμα των αρχικών δεδομένων. Διαφορετικά, καλείται το περιγραφόμενο σχήμα προσθήκης διανύσματος κανόνας τριγώνου.
Γεωμετρικά, η προσθήκη διανυσμάτων μοιάζει με αυτό:
Για μη γραμμικά διανύσματα:
Για συγγραμμικά (συνκατευθυντικά ή αντίθετα) διανύσματα:
Λαμβάνοντας ως βάση το σχήμα που περιγράφηκε παραπάνω, έχουμε την ευκαιρία να εκτελέσουμε τη λειτουργία της προσθήκης διανυσμάτων σε ποσότητα μεγαλύτερη από 2: προσθέτοντας κάθε επόμενο διάνυσμα με τη σειρά.
Ορισμός 6
Εισαγωγή: διανύσματα α → , β → , γ →, δ → . Από ένα αυθαίρετο σημείο Α στο επίπεδο είναι απαραίτητο να σχεδιάσουμε ένα τμήμα (διάνυσμα) ίσο με το διάνυσμα α →; τότε από το τέλος του προκύπτοντος διανύσματος παραλείπεται ένα διάνυσμα ίσο με το διάνυσμα β →; Στη συνέχεια, τα επόμενα διανύσματα σχεδιάζονται χρησιμοποιώντας την ίδια αρχή. Το τελικό σημείο του τελευταίου αναβαλλόμενου διανύσματος θα είναι το σημείο Β και το προκύπτον τμήμα (διάνυσμα) Α Β →– το άθροισμα όλων των αρχικών δεδομένων. Το περιγραφόμενο σχήμα για την προσθήκη πολλών διανυσμάτων ονομάζεται επίσης κανόνας πολυγώνου .
Γεωμετρικά μοιάζει με αυτό:
Ορισμός 7
Ένα ξεχωριστό σχέδιο δράσης για διανυσματική αφαίρεσηόχι επειδή ουσιαστικά μια διανυσματική διαφορά α →Και β →είναι το άθροισμα των διανυσμάτων α →Και - β → .
Ορισμός 8Για να εκτελέσετε την ενέργεια του πολλαπλασιασμού ενός διανύσματος με έναν ορισμένο αριθμό k, πρέπει να ληφθούν υπόψη οι ακόλουθοι κανόνες:
- εάν k > 1, τότε αυτός ο αριθμός θα οδηγήσει στο να τεντωθεί το διάνυσμα k φορές.
- αν 0< k < 1 , то это число приведет к сжатию вектора в
1 k φορές?
- εάν κ< 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
- εάν k = 1, τότε το διάνυσμα παραμένει το ίδιο.
- εάν ένας από τους παράγοντες είναι μηδενικό διάνυσμα ή αριθμός ίσος με μηδέν, το αποτέλεσμα του πολλαπλασιασμού θα είναι μηδενικό διάνυσμα.
Αρχικά δεδομένα:
1) διάνυσμα α →και αριθμός k = 2;
2) διάνυσμα β →και αριθμός k = - 1 3 .
Γεωμετρικά, το αποτέλεσμα του πολλαπλασιασμού σύμφωνα με τους παραπάνω κανόνες θα μοιάζει με αυτό:
Οι πράξεις σε διανύσματα που περιγράφονται παραπάνω έχουν ιδιότητες, μερικές από τις οποίες είναι προφανείς, ενώ άλλες μπορούν να αιτιολογηθούν γεωμετρικά.
Εισαγωγή: διανύσματα α → , β → , γ →και αυθαίρετους πραγματικούς αριθμούς λ και μ.
Οι ιδιότητες της ανταλλαξιμότητας και της συσχέτισης καθιστούν δυνατή την προσθήκη διανυσμάτων με οποιαδήποτε σειρά.
Οι αναφερόμενες ιδιότητες των πράξεων σας επιτρέπουν να πραγματοποιήσετε τους απαραίτητους μετασχηματισμούς διανυσματικών-αριθμητικών παραστάσεων με παρόμοιο τρόπο με τους συνηθισμένους αριθμητικούς. Ας το δούμε αυτό με ένα παράδειγμα.
Παράδειγμα 1
Εργο:απλοποιήστε την έκφραση a → - 2 · (b → + 3 · a →)
Λύση
- χρησιμοποιώντας τη δεύτερη ιδιότητα κατανομής, παίρνουμε: a → - 2 · (b → + 3 · a →) = a → - 2 · b → - 2 · (3 · a →)
- χρησιμοποιούμε τη συσχετιστική ιδιότητα του πολλαπλασιασμού, η έκφραση θα έχει την ακόλουθη μορφή: a → - 2 · b → - 2 · (3 · a →) = a → - 2 · b → - (2 · 3) · a → = a → - 2 · b → - 6 a →
- χρησιμοποιώντας την ιδιότητα commutativity, ανταλλάσσουμε τους όρους: a → - 2 b → - 6 a → = a → - 6 a → - 2 b →
- τότε χρησιμοποιώντας την πρώτη ιδιότητα κατανομής παίρνουμε: a → - 6 · a → - 2 · b → = (1 - 6) · a → - 2 · b → = - 5 · a → - 2 · b → Μια σύντομη σημειογραφία της λύσης θα μοιάζει με αυτό: a → - 2 · (b → + 3 · a →) = a → - 2 · b → - 2 · 3 · a → = 5 · a → - 2 · b →
Απάντηση: a → - 2 · (b → + 3 · a →) = - 5 · a → - 2 · b →
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
