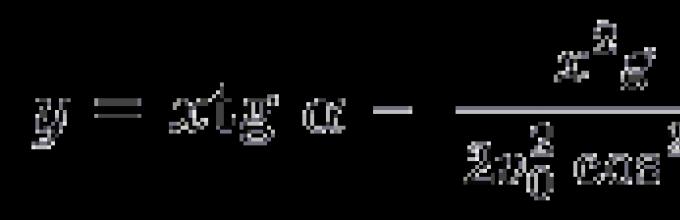Μαθηματική μοντελοποίηση

1. Τι είναι η μαθηματική μοντελοποίηση;

Από τα μέσα του 20ου αιώνα. Οι μαθηματικές μέθοδοι και οι υπολογιστές άρχισαν να χρησιμοποιούνται ευρέως σε διάφορους τομείς της ανθρώπινης δραστηριότητας. Έχουν προκύψει νέοι κλάδοι όπως «μαθηματικά οικονομικά», «μαθηματική χημεία», «μαθηματική γλωσσολογία» κ.λπ., μελετώντας μαθηματικά μοντέλα σχετικών αντικειμένων και φαινομένων, καθώς και μεθόδους μελέτης αυτών των μοντέλων.

Ένα μαθηματικό μοντέλο είναι μια κατά προσέγγιση περιγραφή οποιασδήποτε κατηγορίας φαινομένων ή αντικειμένων του πραγματικού κόσμου στη γλώσσα των μαθηματικών. Ο κύριος σκοπός της μοντελοποίησης είναι να εξερευνήσει αυτά τα αντικείμενα και να προβλέψει τα αποτελέσματα των μελλοντικών παρατηρήσεων. Ωστόσο, το μόντελινγκ είναι επίσης μια μέθοδος κατανόησης του κόσμου γύρω μας, καθιστώντας δυνατό τον έλεγχό του.

Η μαθηματική μοντελοποίηση και το σχετικό πείραμα υπολογιστή είναι απαραίτητα σε περιπτώσεις όπου ένα πείραμα πλήρους κλίμακας είναι αδύνατο ή δύσκολο για τον ένα ή τον άλλο λόγο. Για παράδειγμα, είναι αδύνατο να οργανωθεί ένα φυσικό πείραμα στην ιστορία για να ελέγξει «τι θα είχε συμβεί αν...» Είναι αδύνατο να ελέγξουμε την ορθότητα μιας ή της άλλης κοσμολογικής θεωρίας. Είναι πιθανό, αλλά απίθανο να είναι λογικό, να πειραματιστούμε με την εξάπλωση μιας ασθένειας, όπως η πανώλη, ή να πραγματοποιήσουμε μια πυρηνική έκρηξη για να μελετήσουμε τις συνέπειές της. Όλα αυτά όμως μπορούν να γίνουν σε υπολογιστή κατασκευάζοντας πρώτα μαθηματικά μοντέλα των φαινομένων που μελετώνται.

2. Κύρια στάδια μαθηματικής μοντελοποίησης

1) Πρότυπο κτίριο. Σε αυτό το στάδιο, ορίζεται κάποιο «μη μαθηματικό» αντικείμενο - ένα φυσικό φαινόμενο, σχεδιασμός, οικονομικό σχέδιο, διαδικασία παραγωγής κ.λπ. Σε αυτή την περίπτωση, κατά κανόνα, είναι δύσκολη η σαφής περιγραφή της κατάστασης. Αρχικά, εντοπίζονται τα κύρια χαρακτηριστικά του φαινομένου και οι μεταξύ τους συνδέσεις σε ποιοτικό επίπεδο. Στη συνέχεια οι διαπιστωμένες ποιοτικές εξαρτήσεις διατυπώνονται στη γλώσσα των μαθηματικών, δηλαδή κατασκευάζεται ένα μαθηματικό μοντέλο. Αυτό είναι το πιο δύσκολο στάδιο του μόντελινγκ.

2) Επίλυση του μαθηματικού προβλήματος στο οποίο οδηγεί το μοντέλο. Σε αυτό το στάδιο, δίνεται μεγάλη προσοχή στην ανάπτυξη αλγορίθμων και αριθμητικών μεθόδων για την επίλυση του προβλήματος σε υπολογιστή, με τη βοήθεια των οποίων μπορεί να βρεθεί το αποτέλεσμα με την απαιτούμενη ακρίβεια και σε αποδεκτό χρόνο.

3) Ερμηνεία των συνεπειών που προέκυψαν από το μαθηματικό μοντέλο.Οι συνέπειες που προκύπτουν από το μοντέλο στη γλώσσα των μαθηματικών ερμηνεύονται στη γλώσσα που είναι αποδεκτή στο πεδίο.

4) Έλεγχος καταλληλότητας του μοντέλου.Σε αυτό το στάδιο, προσδιορίζεται εάν τα πειραματικά αποτελέσματα συμφωνούν με τις θεωρητικές συνέπειες του μοντέλου με μια ορισμένη ακρίβεια.

5) Τροποποίηση του μοντέλου.Σε αυτό το στάδιο, είτε το μοντέλο είναι πολύπλοκο ώστε να είναι πιο κατάλληλο για την πραγματικότητα, είτε απλοποιείται προκειμένου να επιτευχθεί μια πρακτικά αποδεκτή λύση.

3. Ταξινόμηση μοντέλων

Τα μοντέλα μπορούν να ταξινομηθούν σύμφωνα με διαφορετικά κριτήρια. Για παράδειγμα, ανάλογα με τη φύση των προβλημάτων που επιλύονται, τα μοντέλα μπορούν να χωριστούν σε λειτουργικά και δομικά. Στην πρώτη περίπτωση, όλες οι ποσότητες που χαρακτηρίζουν ένα φαινόμενο ή αντικείμενο εκφράζονται ποσοτικά. Επιπλέον, ορισμένες από αυτές θεωρούνται ως ανεξάρτητες μεταβλητές, ενώ άλλες θεωρούνται ως συναρτήσεις αυτών των μεγεθών. Ένα μαθηματικό μοντέλο είναι συνήθως ένα σύστημα εξισώσεων διαφόρων τύπων (διαφορικές, αλγεβρικές κ.λπ.) που καθορίζουν ποσοτικές σχέσεις μεταξύ των υπό εξέταση μεγεθών. Στη δεύτερη περίπτωση, το μοντέλο χαρακτηρίζει τη δομή ενός σύνθετου αντικειμένου που αποτελείται από μεμονωμένα μέρη, μεταξύ των οποίων υπάρχουν ορισμένες συνδέσεις. Συνήθως, αυτές οι συνδέσεις δεν είναι ποσοτικοποιήσιμες. Για την κατασκευή τέτοιων μοντέλων, είναι βολικό να χρησιμοποιηθεί η θεωρία γραφημάτων. Γράφημα είναι ένα μαθηματικό αντικείμενο που αντιπροσωπεύει ένα σύνολο σημείων (κορυφών) σε ένα επίπεδο ή σε χώρο, μερικά από τα οποία συνδέονται με γραμμές (άκρες).

Με βάση τη φύση των αρχικών δεδομένων και αποτελεσμάτων, τα μοντέλα πρόβλεψης μπορούν να χωριστούν σε ντετερμινιστικά και πιθανοτικά-στατιστικά. Τα μοντέλα του πρώτου τύπου κάνουν συγκεκριμένες, ξεκάθαρες προβλέψεις. Τα μοντέλα του δεύτερου τύπου βασίζονται σε στατιστικές πληροφορίες και οι προβλέψεις που λαμβάνονται με τη βοήθειά τους είναι πιθανολογικού χαρακτήρα.

4. Παραδείγματα μαθηματικών μοντέλων

1) Προβλήματα σχετικά με την κίνηση ενός βλήματος.

Εξετάστε το ακόλουθο μηχανικό πρόβλημα.

Το βλήμα εκτοξεύεται από τη Γη με αρχική ταχύτητα v 0 = 30 m/s υπό γωνία a = 45° ως προς την επιφάνειά του. απαιτείται να βρει την τροχιά της κίνησής του και την απόσταση S μεταξύ του σημείου έναρξης και του τερματισμού αυτής της τροχιάς.

Στη συνέχεια, όπως είναι γνωστό από ένα μάθημα σχολικής φυσικής, η κίνηση ενός βλήματος περιγράφεται από τους τύπους:

όπου t είναι ο χρόνος, g = 10 m/s 2 είναι η επιτάχυνση της βαρύτητας. Αυτοί οι τύποι παρέχουν ένα μαθηματικό μοντέλο του προβλήματος. Εκφράζοντας t έως x από την πρώτη εξίσωση και αντικαθιστώντας την με τη δεύτερη, λαμβάνουμε την εξίσωση για την τροχιά του βλήματος:

Αυτή η καμπύλη (παραβολή) τέμνει τον άξονα x σε δύο σημεία: x 1 = 0 (αρχή της τροχιάς) και (τόπος που έπεσε το βλήμα). Αντικαθιστώντας τις δεδομένες τιμές των v0 και a στους προκύπτοντες τύπους, λαμβάνουμε

απάντηση: y = x – 90x 2, S = 90 m.

Σημειώστε ότι κατά την κατασκευή αυτού του μοντέλου χρησιμοποιήθηκαν ορισμένες υποθέσεις: για παράδειγμα, θεωρείται ότι η Γη είναι επίπεδη και ο αέρας και η περιστροφή της Γης δεν επηρεάζουν την κίνηση του βλήματος.

2) Πρόβλημα σχετικά με μια δεξαμενή με τη μικρότερη επιφάνεια.

Απαιτείται να βρεθεί το ύψος h 0 και η ακτίνα r 0 μιας δεξαμενής από κασσίτερο όγκου V = 30 m 3, που έχει σχήμα κλειστού κυκλικού κυλίνδρου, στον οποίο το εμβαδόν επιφάνειάς του S είναι ελάχιστο (στην περίπτωση αυτή το λιγότερο ποσότητα κασσίτερου θα χρησιμοποιηθεί για την παραγωγή του).

Ας γράψουμε τους παρακάτω τύπους για τον όγκο και την επιφάνεια ενός κυλίνδρου ύψους h και ακτίνας r:

V = p r 2 h, S = 2p r(r + h).

Εκφράζοντας τα h έως r και V από τον πρώτο τύπο και αντικαθιστώντας την έκφραση που προκύπτει με τον δεύτερο, παίρνουμε:

Έτσι, από μαθηματική άποψη, το πρόβλημα καταλήγει στον προσδιορισμό της τιμής του r στην οποία η συνάρτηση S(r) φτάνει στο ελάχιστο της. Ας βρούμε εκείνες τις τιμές του r 0 για τις οποίες η παράγωγος

πάει στο μηδέν: Μπορείτε να ελέγξετε ότι η δεύτερη παράγωγος της συνάρτησης S(r) αλλάζει πρόσημο από μείον σε συν όταν το όρισμα r διέρχεται από το σημείο r 0 . Κατά συνέπεια, στο σημείο r0 η συνάρτηση S(r) έχει ελάχιστο. Η αντίστοιχη τιμή είναι h 0 = 2r 0 . Αντικαθιστώντας τη δεδομένη τιμή V στην έκφραση για r 0 και h 0, λαμβάνουμε την επιθυμητή ακτίνα και ύψος

3) Πρόβλημα μεταφοράς.

Η πόλη διαθέτει δύο αποθήκες αλευριού και δύο φούρνους. Καθημερινά μεταφέρονται 50 τόνοι αλεύρι από την πρώτη αποθήκη και 70 τόνοι από τη δεύτερη στα εργοστάσια, με 40 τόνους στην πρώτη και 80 τόνους στη δεύτερη.

Ας υποδηλώσουμε με ένα ij είναι το κόστος μεταφοράς 1 τόνου αλεύρου από την ιη αποθήκη στην ιη μονάδα (i, j = 1,2). Αφήνω

ένα 11 = 1,2 ρούβλια, ένα 12 = 1,6 ρούβλια, ένα 21 = 0,8 τρίψιμο., ένα 22 = 1 τρίψιμο.

Πώς πρέπει να προγραμματιστεί η μεταφορά ώστε το κόστος της να είναι ελάχιστο;

Ας δώσουμε στο πρόβλημα μια μαθηματική διατύπωση. Ας συμβολίσουμε με x 1 και x 2 την ποσότητα του αλευριού που πρέπει να μεταφερθεί από την πρώτη αποθήκη στο πρώτο και το δεύτερο εργοστάσιο και με x 3 και x 4 - από τη δεύτερη αποθήκη στο πρώτο και το δεύτερο εργοστάσιο, αντίστοιχα. Επειτα:

x 1 + x 2 = 50, x 3 + x 4 = 70, x 1 + x 3 = 40, x 2 + x 4 = 80. (1)

Το συνολικό κόστος όλων των μεταφορών καθορίζεται από τον τύπο

f = 1,2x 1 + 1,6x 2 + 0,8x 3 + x 4.

Από μαθηματική άποψη, το πρόβλημα είναι να βρούμε τέσσερις αριθμούς x 1, x 2, x 3 και x 4 που να ικανοποιούν όλες τις δεδομένες συνθήκες και να δίνουν το ελάχιστο της συνάρτησης f. Ας λύσουμε το σύστημα των εξισώσεων (1) για το xi (i = 1, 2, 3, 4) εξαλείφοντας τους αγνώστους. Το καταλαβαίνουμε

x 1 = x 4 – 30, x 2 = 80 – x 4, x 3 = 70 – x 4, (2)

και το x 4 δεν μπορεί να προσδιοριστεί μοναδικά. Εφόσον x i і 0 (i = 1, 2, 3, 4), από τις εξισώσεις (2) προκύπτει ότι 30Ј x 4 Ј 70. Αντικαθιστώντας την έκφραση για x 1, x 2, x 3 στον τύπο για f, παίρνουμε

f = 148 – 0,2 x 4.

Είναι εύκολο να δούμε ότι το ελάχιστο αυτής της συνάρτησης επιτυγχάνεται στη μέγιστη δυνατή τιμή του x 4, δηλαδή στο x 4 = 70. Οι αντίστοιχες τιμές άλλων αγνώστων καθορίζονται από τους τύπους (2): x 1 = 40, x 2 = 10, x 3 = 0.

4) Το πρόβλημα της ραδιενεργής διάσπασης.

Έστω N(0) ο αρχικός αριθμός ατόμων μιας ραδιενεργής ουσίας και N(t) ο αριθμός των μη διασπώμενων ατόμων τη χρονική στιγμή t. Έχει αποδειχθεί πειραματικά ότι ο ρυθμός μεταβολής του αριθμού αυτών των ατόμων N"(t) είναι ανάλογος του N(t), δηλαδή, N"(t)=–l N(t), l >0 είναι το σταθερά ραδιενέργειας μιας δεδομένης ουσίας. Στο σχολικό μάθημα της μαθηματικής ανάλυσης φαίνεται ότι η λύση αυτής της διαφορικής εξίσωσης έχει τη μορφή N(t) = N(0)e –l t. Ο χρόνος T κατά τον οποίο ο αριθμός των αρχικών ατόμων μειώθηκε στο μισό ονομάζεται χρόνος ημιζωής και είναι ένα σημαντικό χαρακτηριστικό της ραδιενέργειας μιας ουσίας. Για να προσδιορίσουμε το T, πρέπει να βάλουμε τον τύπο Επειτα Για παράδειγμα, για το ραδόνιο l = 2,084 · 10 –6, και επομένως T = 3,15 ημέρες.

5) Το πρόβλημα του πλανόδιου πωλητή.

Ένας ταξιδιώτης πωλητής που ζει στην πόλη A 1 πρέπει να επισκεφτεί τις πόλεις A 2 , A 3 και A 4 , κάθε πόλη ακριβώς μία φορά, και μετά να επιστρέψει πίσω στο A 1 . Είναι γνωστό ότι όλες οι πόλεις συνδέονται σε ζεύγη με δρόμους και τα μήκη των δρόμων b ij μεταξύ των πόλεων A i και A j (i, j = 1, 2, 3, 4) είναι τα εξής:

b 12 = 30, b 14 = 20, b 23 = 50, b 24 = 40, b 13 = 70, b 34 = 60.

Είναι απαραίτητο να καθοριστεί η σειρά επίσκεψης πόλεων στις οποίες το μήκος της αντίστοιχης διαδρομής είναι ελάχιστο.

Ας απεικονίσουμε κάθε πόλη ως ένα σημείο στο επίπεδο και ας τη σημειώσουμε με την αντίστοιχη ετικέτα Ai (i = 1, 2, 3, 4). Ας συνδέσουμε αυτά τα σημεία με ευθείες γραμμές: θα αντιπροσωπεύουν δρόμους μεταξύ πόλεων. Για κάθε «δρόμο» υποδεικνύουμε το μήκος του σε χιλιόμετρα (Εικ. 2). Το αποτέλεσμα είναι ένα γράφημα - ένα μαθηματικό αντικείμενο που αποτελείται από ένα ορισμένο σύνολο σημείων στο επίπεδο (που ονομάζονται κορυφές) και ένα ορισμένο σύνολο γραμμών που συνδέουν αυτά τα σημεία (που ονομάζονται ακμές). Επιπλέον, αυτό το γράφημα έχει ετικέτα, καθώς στις κορυφές και τις ακμές του αντιστοιχίζονται ορισμένες ετικέτες - αριθμοί (άκρες) ή σύμβολα (κορυφές). Ένας κύκλος σε ένα γράφημα είναι μια ακολουθία κορυφών V 1 , V 2 , ..., V k , V 1 έτσι ώστε οι κορυφές V 1 , ..., V k να είναι διαφορετικές και οποιοδήποτε ζεύγος κορυφών V i , V i+1 (i = 1, ..., k – 1) και το ζεύγος V 1, V k συνδέονται με μια ακμή. Έτσι, το πρόβλημα που εξετάζεται είναι να βρεθεί ένας κύκλος στο γράφημα που διέρχεται και από τις τέσσερις κορυφές για τις οποίες το άθροισμα όλων των βαρών των ακμών είναι ελάχιστο. Ας αναζητήσουμε όλους τους διαφορετικούς κύκλους που διέρχονται από τέσσερις κορυφές και ξεκινούν από το A 1:

1) A 1, A 4, A 3, A 2, A 1;
2) A 1, A 3, A 2, A 4, A 1;
3) Α 1, Α 3, Α 4, Α 2, Α 1.

Ας βρούμε τώρα τα μήκη αυτών των κύκλων (σε km): L 1 = 160, L 2 = 180, L 3 = 200. Άρα, η διαδρομή με το μικρότερο μήκος είναι η πρώτη.

Σημειώστε ότι εάν υπάρχουν n κορυφές σε ένα γράφημα και όλες οι κορυφές συνδέονται ανά ζεύγη με ακμές (ένα τέτοιο γράφημα ονομάζεται πλήρες), τότε ο αριθμός των κύκλων που διέρχονται από όλες τις κορυφές είναι Επομένως, στην περίπτωσή μας υπάρχουν ακριβώς τρεις κύκλοι.

6) Το πρόβλημα της εύρεσης σύνδεσης μεταξύ της δομής και των ιδιοτήτων των ουσιών.

Ας δούμε πολλές χημικές ενώσεις που ονομάζονται κανονικά αλκάνια. Αποτελούνται από n άτομα άνθρακα και n + 2 άτομα υδρογόνου (n = 1, 2 ...), διασυνδεδεμένα όπως φαίνεται στο σχήμα 3 για n = 3. Ας είναι γνωστές οι πειραματικές τιμές των σημείων βρασμού αυτών των ενώσεων:

y e (3) = – 42°, y e (4) = 0°, y e (5) = 28°, y e (6) = 69°.

Απαιτείται να βρεθεί μια κατά προσέγγιση σχέση μεταξύ του σημείου βρασμού και του αριθμού n για αυτές τις ενώσεις. Ας υποθέσουμε ότι αυτή η εξάρτηση έχει τη μορφή

y" ένα n+b,

Οπου ένα, b - σταθερές που πρέπει να προσδιοριστούν. Να βρω ένακαι β αντικαθιστούμε σε αυτόν τον τύπο διαδοχικά n = 3, 4, 5, 6 και τις αντίστοιχες τιμές των σημείων βρασμού. Εχουμε:

– 42 » 3 ένα+ β, 0 » 4 ένα+ β, 28 » 5 ένα+ β, 69 » 6 ένα+ β.

Για να καθορίσει το καλύτερο ένακαι β υπάρχουν πολλές διαφορετικές μέθοδοι. Ας χρησιμοποιήσουμε τα πιο απλά από αυτά. Ας εκφράσουμε το β μέσω ένααπό αυτές τις εξισώσεις:

β» – 42 – 3 ένα, β" – 4 ένα, β » 28 – 5 ένα, β » 69 – 6 ένα.

Ας πάρουμε τον αριθμητικό μέσο όρο αυτών των τιμών ως το επιθυμητό b, δηλαδή βάζουμε b » 16 – 4,5 ένα. Ας αντικαταστήσουμε αυτή την τιμή του b στο αρχικό σύστημα εξισώσεων και, υπολογίζοντας ένα, παίρνουμε για ένατις ακόλουθες τιμές: ένα» 37, ένα» 28, ένα» 28, ένα« 36. Ας πάρουμε όπως απαιτείται έναη μέση τιμή αυτών των αριθμών, δηλαδή ας βάλουμε ένα" 34. Άρα, η απαιτούμενη εξίσωση έχει τη μορφή

y » 34n – 139.

Ας ελέγξουμε την ακρίβεια του μοντέλου στις αρχικές τέσσερις ενώσεις, για τις οποίες υπολογίζουμε τα σημεία βρασμού χρησιμοποιώντας τον τύπο που προκύπτει:

y р (3) = – 37°, y р (4) = – 3°, y р (5) = 31°, y р (6) = 65°.

Έτσι, το σφάλμα στον υπολογισμό αυτής της ιδιότητας για αυτές τις ενώσεις δεν υπερβαίνει τις 5°. Χρησιμοποιούμε την εξίσωση που προκύπτει για να υπολογίσουμε το σημείο βρασμού μιας ένωσης με n = 7, το οποίο δεν περιλαμβάνεται στο αρχικό σύνολο, για το οποίο αντικαθιστούμε το n = 7 σε αυτήν την εξίσωση: y р (7) = 99°. Το αποτέλεσμα ήταν αρκετά ακριβές: είναι γνωστό ότι η πειραματική τιμή του σημείου βρασμού y e (7) = 98°.

7) Το πρόβλημα του προσδιορισμού της αξιοπιστίας ενός ηλεκτρικού κυκλώματος.

Εδώ θα δούμε ένα παράδειγμα πιθανολογικού μοντέλου. Πρώτον, παρουσιάζουμε κάποιες πληροφορίες από τη θεωρία πιθανοτήτων - μια μαθηματική επιστήμη που μελετά τα μοτίβα τυχαίων φαινομένων που παρατηρούνται κατά την επαναλαμβανόμενη επανάληψη των πειραμάτων. Ας ονομάσουμε ένα τυχαίο γεγονός A πιθανό αποτέλεσμα κάποιου πειράματος. Τα συμβάντα A 1, ..., A k σχηματίζουν μια πλήρη ομάδα εάν ένα από αυτά συμβαίνει απαραίτητα ως αποτέλεσμα του πειράματος. Τα συμβάντα ονομάζονται ασύμβατα εάν δεν μπορούν να συμβούν ταυτόχρονα σε μία εμπειρία. Έστω το γεγονός Α να συμβεί m φορές κατά τη διάρκεια μιας n-πλάσιας επανάληψης του πειράματος. Η συχνότητα του γεγονότος Α είναι ο αριθμός W = . Προφανώς, η τιμή του W δεν μπορεί να προβλεφθεί με ακρίβεια μέχρι να πραγματοποιηθεί μια σειρά από n πειράματα. Ωστόσο, η φύση των τυχαίων γεγονότων είναι τέτοια που στην πράξη παρατηρείται μερικές φορές το ακόλουθο αποτέλεσμα: καθώς αυξάνεται ο αριθμός των πειραμάτων, η τιμή πρακτικά παύει να είναι τυχαία και σταθεροποιείται γύρω από κάποιον μη τυχαίο αριθμό P(A), που ονομάζεται πιθανότητα το συμβάν Α. Για ένα αδύνατο γεγονός (το οποίο δεν συμβαίνει ποτέ σε ένα πείραμα) P(A)=0, και για ένα αξιόπιστο γεγονός (που συμβαίνει πάντα στην εμπειρία) P(A)=1. Αν τα γεγονότα A 1 , ..., A k σχηματίζουν μια πλήρη ομάδα ασύμβατων γεγονότων, τότε P(A 1)+...+P(A k)=1.

Έστω, για παράδειγμα, το πείραμα αποτελείται από το πέταγμα ενός ζαριού και την παρατήρηση του αριθμού των σημείων X. Στη συνέχεια, μπορούμε να εισαγάγουμε τα ακόλουθα τυχαία γεγονότα A i = (X = i), i = 1, ..., 6. σχηματίζουν μια πλήρη ομάδα ασυμβίβαστων εξίσου πιθανών γεγονότων, επομένως P(A i) = (i = 1, ..., 6).

Το άθροισμα των γεγονότων Α και Β είναι το γεγονός Α + Β, το οποίο συνίσταται στο γεγονός ότι τουλάχιστον ένα από αυτά συμβαίνει στην εμπειρία. Το γινόμενο των γεγονότων Α και Β είναι το γεγονός ΑΒ, το οποίο αποτελείται από την ταυτόχρονη εμφάνιση αυτών των γεγονότων. Για ανεξάρτητα συμβάντα Α και Β, ισχύουν οι ακόλουθοι τύποι:

Ρ(ΑΒ) = Ρ(Α) Ρ(Β), Ρ(Α + Β) = Ρ(Α) + Ρ(Β).

8) Ας εξετάσουμε τώρα τα ακόλουθα έργο. Ας υποθέσουμε ότι τρία στοιχεία συνδέονται σε σειρά σε ένα ηλεκτρικό κύκλωμα και λειτουργούν ανεξάρτητα το ένα από το άλλο. Οι πιθανότητες αστοχίας του 1ου, 2ου και 3ου στοιχείου είναι αντίστοιχα ίσες με P1 = 0,1, P2 = 0,15, P3 = 0,2. Θα θεωρήσουμε ένα κύκλωμα αξιόπιστο εάν η πιθανότητα να μην υπάρχει ρεύμα στο κύκλωμα δεν είναι μεγαλύτερη από 0,4. Είναι απαραίτητο να προσδιοριστεί εάν ένα δεδομένο κύκλωμα είναι αξιόπιστο.

Δεδομένου ότι τα στοιχεία είναι συνδεδεμένα σε σειρά, δεν θα υπάρχει ρεύμα στο κύκλωμα (γεγονός Α) εάν τουλάχιστον ένα από τα στοιχεία αποτύχει. Έστω A i το γεγονός που λειτουργεί το i-ο στοιχείο (i = 1, 2, 3). Τότε P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Προφανώς, το A 1 A 2 A 3 είναι ένα γεγονός στο οποίο και τα τρία στοιχεία λειτουργούν ταυτόχρονα, και

Ρ(Α 1 Α 2 Α 3) = Ρ(Α 1) Ρ(Α 2) Ρ(Α 3) = 0,612.

Τότε P(A) + P(A 1 A 2 A 3) = 1, άρα P(A) = 0,388< 0,4. Следовательно, цепь является надежной.

Συμπερασματικά, σημειώνουμε ότι τα παραδείγματα μαθηματικών μοντέλων (συμπεριλαμβανομένων λειτουργικών και δομικών, ντετερμινιστικών και πιθανολογικών) είναι ενδεικτικά και, προφανώς, δεν εξαντλούν την ποικιλία των μαθηματικών μοντέλων που προκύπτουν στις φυσικές και ανθρωπιστικές επιστήμες.

Σε αυτό το άρθρο, προσφέρουμε παραδείγματα μαθηματικών μοντέλων. Επιπλέον, θα δώσουμε προσοχή στα στάδια δημιουργίας μοντέλων και θα αναλύσουμε ορισμένα προβλήματα που σχετίζονται με τη μαθηματική μοντελοποίηση.

Ένα άλλο ερώτημα που έχουμε είναι τα μαθηματικά μοντέλα στα οικονομικά, παραδείγματα των οποίων θα δούμε τον ορισμό λίγο αργότερα. Προτείνουμε να ξεκινήσουμε τη συζήτησή μας με την ίδια την έννοια του "μοντέλου", να εξετάσουμε εν συντομία την ταξινόμησή τους και να προχωρήσουμε στις κύριες ερωτήσεις μας.

Η έννοια του "μοντέλου"

Ακούμε συχνά τη λέξη «μοντέλο». Τι είναι αυτό? Αυτός ο όρος έχει πολλούς ορισμούς, εδώ είναι μόνο τρεις από αυτούς:

ένα συγκεκριμένο αντικείμενο που δημιουργείται για να λαμβάνει και να αποθηκεύει πληροφορίες, που αντικατοπτρίζουν ορισμένες ιδιότητες ή χαρακτηριστικά, κ.λπ., του πρωτοτύπου αυτού του αντικειμένου (αυτό το συγκεκριμένο αντικείμενο μπορεί να εκφραστεί με διάφορες μορφές: νοητικό, περιγραφή με χρήση πινακίδων κ.λπ.)
Ένα μοντέλο σημαίνει επίσης μια αναπαράσταση μιας συγκεκριμένης κατάστασης, ζωής ή διαχείρισης.
ένα μοντέλο μπορεί να είναι ένα μειωμένο αντίγραφο ενός αντικειμένου (δημιουργούνται για πιο λεπτομερή μελέτη και ανάλυση, καθώς το μοντέλο αντικατοπτρίζει τη δομή και τις σχέσεις).

Με βάση όλα όσα ειπώθηκαν νωρίτερα, μπορούμε να βγάλουμε ένα μικρό συμπέρασμα: το μοντέλο σας επιτρέπει να μελετήσετε λεπτομερώς ένα σύνθετο σύστημα ή αντικείμενο.

Όλα τα μοντέλα μπορούν να ταξινομηθούν σύμφωνα με ορισμένα χαρακτηριστικά:

ανά τομέα χρήσης (εκπαιδευτικό, πειραματικό, επιστημονικό και τεχνικό, gaming, προσομοίωση)·
από δυναμική (στατική και δυναμική).
ανά κλάδο γνώσης (φυσική, χημική, γεωγραφική, ιστορική, κοινωνιολογική, οικονομική, μαθηματική)·
με τη μέθοδο της παρουσίασης (υλική και ενημερωτική).

Τα μοντέλα πληροφοριών, με τη σειρά τους, χωρίζονται σε συμβολικά και λεκτικά. Και συμβολικές - σε υπολογιστές και μη υπολογιστές. Τώρα ας προχωρήσουμε σε μια λεπτομερή εξέταση παραδειγμάτων του μαθηματικού μοντέλου.

Μαθηματικό μοντέλο

Όπως μπορείτε να μαντέψετε, ένα μαθηματικό μοντέλο αντικατοπτρίζει οποιαδήποτε χαρακτηριστικά ενός αντικειμένου ή φαινομένου χρησιμοποιώντας ειδικά μαθηματικά σύμβολα. Τα μαθηματικά χρειάζονται για να μοντελοποιηθούν τα πρότυπα του περιβάλλοντος κόσμου στη δική τους συγκεκριμένη γλώσσα.

Η μέθοδος της μαθηματικής μοντελοποίησης ξεκίνησε πριν από πολύ καιρό, πριν από χιλιάδες χρόνια, μαζί με την έλευση αυτής της επιστήμης. Ωστόσο, το έναυσμα για την ανάπτυξη αυτής της μεθόδου μοντελοποίησης δόθηκε από την εμφάνιση των υπολογιστών (ηλεκτρονικοί υπολογιστές).

Τώρα ας περάσουμε στην ταξινόμηση. Μπορεί επίσης να πραγματοποιηθεί σύμφωνα με ορισμένα σημάδια. Παρουσιάζονται στον παρακάτω πίνακα.

Προτείνουμε να σταματήσουμε και να ρίξουμε μια πιο προσεκτική ματιά στην τελευταία ταξινόμηση, καθώς αντικατοπτρίζει τα γενικά πρότυπα μοντελοποίησης και τους στόχους των μοντέλων που δημιουργούνται.

Περιγραφικά μοντέλα

Σε αυτό το κεφάλαιο, προτείνουμε να σταθούμε λεπτομερέστερα σε περιγραφικά μαθηματικά μοντέλα. Για να γίνουν όλα ξεκάθαρα, θα δοθεί ένα παράδειγμα.

Ας ξεκινήσουμε με το γεγονός ότι αυτή η άποψη μπορεί να ονομαστεί περιγραφική. Αυτό οφείλεται στο γεγονός ότι κάνουμε απλώς υπολογισμούς και προβλέψεις, αλλά δεν μπορούμε με κανέναν τρόπο να επηρεάσουμε την έκβαση του γεγονότος.

Ένα εντυπωσιακό παράδειγμα ενός περιγραφικού μαθηματικού μοντέλου είναι ο υπολογισμός της διαδρομής πτήσης, της ταχύτητας και της απόστασης από τη Γη ενός κομήτη που εισέβαλε στις εκτάσεις του ηλιακού μας συστήματος. Αυτό το μοντέλο είναι περιγραφικό, καθώς όλα τα αποτελέσματα που λαμβάνονται μπορούν μόνο να μας προειδοποιήσουν για οποιονδήποτε κίνδυνο. Δυστυχώς, δεν μπορούμε να επηρεάσουμε την έκβαση της εκδήλωσης. Ωστόσο, με βάση τους υπολογισμούς που προέκυψαν, είναι δυνατό να ληφθούν μέτρα για τη διατήρηση της ζωής στη Γη.

Μοντέλα βελτιστοποίησης

Τώρα θα μιλήσουμε λίγο για οικονομικά και μαθηματικά μοντέλα, παραδείγματα των οποίων μπορούν να χρησιμεύσουν ως διαφορετικές τρέχουσες καταστάσεις. Σε αυτή την περίπτωση, μιλάμε για μοντέλα που βοηθούν στην εύρεση της σωστής απάντησης υπό ορισμένες προϋποθέσεις. Σίγουρα έχουν κάποιες παραμέτρους. Για να γίνει απολύτως σαφές, ας δούμε ένα παράδειγμα από τον αγροτικό τομέα.

Έχουμε σιταποθήκη, αλλά τα σιτηρά χαλάνε πολύ γρήγορα. Σε αυτή την περίπτωση, πρέπει να επιλέξουμε τις σωστές συνθήκες θερμοκρασίας και να βελτιστοποιήσουμε τη διαδικασία αποθήκευσης.

Έτσι, μπορούμε να ορίσουμε την έννοια του «μοντέλου βελτιστοποίησης». Με μαθηματική έννοια, είναι ένα σύστημα εξισώσεων (γραμμικών και μη), η λύση των οποίων βοηθά να βρεθεί η βέλτιστη λύση σε μια συγκεκριμένη οικονομική κατάσταση. Εξετάσαμε ένα παράδειγμα μαθηματικού μοντέλου (βελτιστοποίηση), αλλά θα ήθελα να προσθέσω: αυτός ο τύπος ανήκει στην κατηγορία των ακραίων προβλημάτων, βοηθούν στην περιγραφή της λειτουργίας του οικονομικού συστήματος.

Ας σημειώσουμε μια ακόμη απόχρωση: τα μοντέλα μπορεί να είναι διαφορετικής φύσης (δείτε τον παρακάτω πίνακα).

Πολυκριτηριακά μοντέλα

Τώρα σας προσκαλούμε να μιλήσουμε λίγο για το μαθηματικό μοντέλο βελτιστοποίησης πολλαπλών κριτηρίων. Πριν από αυτό, δώσαμε ένα παράδειγμα μαθηματικού μοντέλου για τη βελτιστοποίηση μιας διαδικασίας σύμφωνα με οποιοδήποτε κριτήριο, αλλά τι γίνεται αν υπάρχουν πολλά από αυτά;

Χαρακτηριστικό παράδειγμα μιας πολυκριτηριακής εργασίας είναι η οργάνωση σωστής, υγιεινής και ταυτόχρονα οικονομικής διατροφής για μεγάλες ομάδες ανθρώπων. Τέτοιες εργασίες συναντώνται συχνά στο στρατό, στις σχολικές καντίνες, στις καλοκαιρινές κατασκηνώσεις, στα νοσοκομεία κ.λπ.

Ποια κριτήρια μας δίνονται σε αυτό το έργο;

Η διατροφή πρέπει να είναι υγιεινή.
Τα έξοδα διατροφής πρέπει να είναι ελάχιστα.

Όπως μπορείτε να δείτε, αυτοί οι στόχοι δεν συμπίπτουν καθόλου. Αυτό σημαίνει ότι κατά την επίλυση ενός προβλήματος, είναι απαραίτητο να αναζητήσετε μια βέλτιστη λύση, μια ισορροπία μεταξύ δύο κριτηρίων.

Μοντέλα παιχνιδιών

Όταν μιλάμε για μοντέλα παιχνιδιών, είναι απαραίτητο να κατανοήσουμε την έννοια της «θεωρίας παιγνίων». Με απλά λόγια, αυτά τα μοντέλα αντικατοπτρίζουν μαθηματικά μοντέλα πραγματικών συγκρούσεων. Απλά πρέπει να καταλάβετε ότι, σε αντίθεση με μια πραγματική σύγκρουση, το μαθηματικό μοντέλο του παιχνιδιού έχει τους δικούς του συγκεκριμένους κανόνες.

Τώρα θα παρέχουμε ελάχιστες πληροφορίες από τη θεωρία παιγνίων που θα σας βοηθήσουν να κατανοήσετε τι είναι ένα μοντέλο παιχνιδιού. Και έτσι, το μοντέλο περιέχει απαραίτητα πάρτι (δύο ή περισσότερα), που συνήθως ονομάζονται παίκτες.

Όλα τα μοντέλα έχουν ορισμένα χαρακτηριστικά.

Το μοντέλο παιχνιδιού μπορεί να είναι ζευγαρωμένο ή πολλαπλό. Αν έχουμε δύο υποκείμενα, τότε η σύγκρουση είναι ζευγαρωμένη, αν υπάρχουν περισσότερα, είναι πολλαπλή. Μπορείτε επίσης να διακρίνετε ένα ανταγωνιστικό παιχνίδι, ονομάζεται επίσης παιχνίδι μηδενικού αθροίσματος. Αυτό είναι ένα μοντέλο στο οποίο το κέρδος ενός από τους συμμετέχοντες είναι ίσο με την απώλεια του άλλου.

Μοντέλα προσομοίωσης

Σε αυτή την ενότητα θα δώσουμε προσοχή στα μαθηματικά μοντέλα προσομοίωσης. Παραδείγματα εργασιών περιλαμβάνουν:

μοντέλο δυναμικής πληθυσμού μικροοργανισμών.
μοντέλο μοριακής κίνησης, και ούτω καθεξής.

Σε αυτή την περίπτωση, μιλάμε για μοντέλα που είναι όσο το δυνατόν πιο κοντά σε πραγματικές διαδικασίες. Σε γενικές γραμμές, μιμούνται κάποια εκδήλωση στη φύση. Στην πρώτη περίπτωση, για παράδειγμα, μπορούμε να προσομοιώσουμε τη δυναμική του αριθμού των μυρμηγκιών σε μία αποικία. Ταυτόχρονα, μπορείτε να παρατηρήσετε τη μοίρα του κάθε ατόμου ξεχωριστά. Σε αυτήν την περίπτωση, μια μαθηματική περιγραφή χρησιμοποιείται σπάνια· υπάρχουν πιο συχνά γραπτές συνθήκες:

μετά από πέντε ημέρες το θηλυκό γεννά αυγά.
μετά από είκοσι μέρες το μυρμήγκι πεθαίνει, και ούτω καθεξής.

Έτσι, χρησιμοποιούνται για να περιγράψουν ένα μεγάλο σύστημα. Ένα μαθηματικό συμπέρασμα είναι η επεξεργασία των λαμβανόμενων στατιστικών δεδομένων.

Απαιτήσεις

Είναι πολύ σημαντικό να γνωρίζετε ότι αυτός ο τύπος μοντέλου έχει ορισμένες απαιτήσεις, συμπεριλαμβανομένων εκείνων που αναφέρονται στον παρακάτω πίνακα.

Ευστροφία	Αυτή η ιδιότητα σάς επιτρέπει να χρησιμοποιείτε το ίδιο μοντέλο όταν περιγράφετε παρόμοιες ομάδες αντικειμένων. Είναι σημαντικό να σημειωθεί ότι τα καθολικά μαθηματικά μοντέλα είναι εντελώς ανεξάρτητα από τη φυσική φύση του υπό μελέτη αντικειμένου
Επάρκεια	Είναι σημαντικό να καταλάβετε εδώ ότι αυτή η ιδιότητα σας επιτρέπει να αναπαράγετε πραγματικές διαδικασίες όσο το δυνατόν ακριβέστερα. Σε επιχειρησιακές εργασίες, αυτή η ιδιότητα της μαθηματικής μοντελοποίησης είναι πολύ σημαντική. Ένα παράδειγμα μοντέλου είναι η διαδικασία βελτιστοποίησης της χρήσης ενός συστήματος αερίου. Σε αυτήν την περίπτωση, οι υπολογισμένοι και οι πραγματικοί δείκτες συγκρίνονται, ως αποτέλεσμα, ελέγχεται η ορθότητα του μεταγλωττισμένου μοντέλου
Ακρίβεια	Αυτή η απαίτηση συνεπάγεται τη σύμπτωση των τιμών που λαμβάνουμε κατά τον υπολογισμό του μαθηματικού μοντέλου και των παραμέτρων εισόδου του πραγματικού μας αντικειμένου
Οικονομικός	Η απαίτηση κόστους-αποτελεσματικότητας για οποιοδήποτε μαθηματικό μοντέλο χαρακτηρίζεται από κόστος υλοποίησης. Εάν εργάζεστε με το μοντέλο χειροκίνητα, τότε πρέπει να υπολογίσετε πόσο χρόνο θα χρειαστεί για να λύσετε ένα πρόβλημα χρησιμοποιώντας αυτό το μαθηματικό μοντέλο. Αν μιλάμε για σχεδιασμό με τη βοήθεια υπολογιστή, τότε υπολογίζονται δείκτες χρόνου και κόστους μνήμης υπολογιστή

Στάδια μοντελοποίησης

Συνολικά, η μαθηματική μοντελοποίηση χωρίζεται συνήθως σε τέσσερα στάδια.

Διατύπωση νόμων που συνδέουν μέρη του μοντέλου.
Μελέτη μαθηματικών προβλημάτων.
Προσδιορισμός της σύμπτωσης πρακτικών και θεωρητικών αποτελεσμάτων.
Ανάλυση και εκσυγχρονισμός του μοντέλου.

Οικονομικό και μαθηματικό μοντέλο

Σε αυτήν την ενότητα θα επισημάνουμε εν συντομία το ζήτημα. Παραδείγματα εργασιών περιλαμβάνουν:

διαμόρφωση ενός προγράμματος παραγωγής για την παραγωγή προϊόντων κρέατος που εξασφαλίζει τα μέγιστα παραγωγικά κέρδη·
μεγιστοποίηση του κέρδους του οργανισμού με τον υπολογισμό της βέλτιστης ποσότητας τραπεζιών και καρεκλών που παράγονται σε ένα εργοστάσιο επίπλων, και ούτω καθεξής.

Το οικονομικό-μαθηματικό μοντέλο εμφανίζει την οικονομική αφαίρεση, η οποία εκφράζεται χρησιμοποιώντας μαθηματικούς όρους και σύμβολα.

Μαθηματικό μοντέλο υπολογιστή

Παραδείγματα μαθηματικού μοντέλου υπολογιστή είναι:

υδραυλικά προβλήματα χρησιμοποιώντας διαγράμματα ροής, διαγράμματα, πίνακες κ.λπ.
προβλήματα στη μηχανική στερεών και ούτω καθεξής.

Ένα μοντέλο υπολογιστή είναι μια εικόνα ενός αντικειμένου ή συστήματος, που παρουσιάζεται με τη μορφή:

τραπέζια?
μπλοκ διαγράμματα?
διαγράμματα?
γραφικά, και ούτω καθεξής.

Επιπλέον, αυτό το μοντέλο αντικατοπτρίζει τη δομή και τις διασυνδέσεις του συστήματος.

Κατασκευή οικονομικού και μαθηματικού μοντέλου

Έχουμε ήδη μιλήσει για το τι είναι οικονομικό-μαθηματικό μοντέλο. Ένα παράδειγμα επίλυσης του προβλήματος θα εξεταστεί τώρα. Πρέπει να αναλύσουμε το πρόγραμμα παραγωγής για να εντοπίσουμε ένα αποθεματικό για την αύξηση των κερδών με μια μετατόπιση της ποικιλίας.

Δεν θα εξετάσουμε πλήρως το πρόβλημα, αλλά θα δημιουργήσουμε μόνο ένα οικονομικό και μαθηματικό μοντέλο. Το κριτήριο της αποστολής μας είναι η μεγιστοποίηση του κέρδους. Τότε η συνάρτηση έχει τη μορφή: А=р1*х1+р2*х2..., τείνει στο μέγιστο. Σε αυτό το μοντέλο, p είναι το κέρδος ανά μονάδα και x είναι ο αριθμός των μονάδων που παράγονται. Στη συνέχεια, με βάση το κατασκευασμένο μοντέλο, είναι απαραίτητο να γίνουν υπολογισμοί και να συνοψιστούν.

Ένα παράδειγμα κατασκευής ενός απλού μαθηματικού μοντέλου

Εργο.Ο ψαράς επέστρεψε με τα ακόλουθα αλιεύματα:

8 ψάρια - κάτοικοι των βόρειων θαλασσών.
Το 20% των αλιευμάτων είναι κάτοικοι των νότιων θαλασσών.
Δεν βρέθηκε ούτε ένα ψάρι από το τοπικό ποτάμι.

Πόσα ψάρια αγόρασε στο κατάστημα;

Έτσι, ένα παράδειγμα κατασκευής ενός μαθηματικού μοντέλου αυτού του προβλήματος μοιάζει με αυτό. Συμβολίζουμε τον συνολικό αριθμό των ψαριών με x. Σύμφωνα με την κατάσταση, 0,2x είναι ο αριθμός των ψαριών που ζουν στα νότια γεωγραφικά πλάτη. Τώρα συνδυάζουμε όλες τις διαθέσιμες πληροφορίες και παίρνουμε ένα μαθηματικό μοντέλο του προβλήματος: x=0,2x+8. Λύνουμε την εξίσωση και παίρνουμε την απάντηση στο κύριο ερώτημα: αγόρασε 10 ψάρια στο κατάστημα.

Διάλεξη 1.

ΜΕΘΟΔΟΛΟΓΙΚΕΣ ΒΑΣΙΚΕΣ ΜΟΝΤΕΛΕΥΣΗΣ

Τρέχουσα κατάσταση του προβλήματος της μοντελοποίησης συστήματος

Έννοιες Μοντελοποίησης και Προσομοίωσης

Πρίπλασμαμπορεί να θεωρηθεί ως η αντικατάσταση του υπό μελέτη αντικειμένου (πρωτότυπου) με τη συμβατική του εικόνα, περιγραφή ή άλλο αντικείμενο που ονομάζεται μοντέλοκαι παροχή συμπεριφοράς κοντά στην αρχική μέσα στο πλαίσιο ορισμένων υποθέσεων και αποδεκτών σφαλμάτων. Η μοντελοποίηση εκτελείται συνήθως με στόχο την κατανόηση των ιδιοτήτων του πρωτοτύπου μελετώντας το μοντέλο του και όχι το ίδιο το αντικείμενο. Φυσικά, η μοντελοποίηση δικαιολογείται όταν είναι πιο απλή από τη δημιουργία του ίδιου του πρωτοτύπου ή όταν για κάποιο λόγο είναι καλύτερα να μην δημιουργηθεί καθόλου το πρωτότυπο.

Κάτω από μοντέλονοείται ως φυσικό ή αφηρημένο αντικείμενο, οι ιδιότητες του οποίου είναι κατά μία έννοια παρόμοιες με τις ιδιότητες του υπό μελέτη αντικειμένου.Σε αυτή την περίπτωση, οι απαιτήσεις για το μοντέλο καθορίζονται από το πρόβλημα που επιλύεται και τα διαθέσιμα μέσα. Υπάρχουν ορισμένες γενικές απαιτήσεις για τα μοντέλα:

2) πληρότητα – παροχή στον παραλήπτη όλων των απαραίτητων πληροφοριών

σχετικά με το αντικείμενο?

3) ευελιξία - η ικανότητα αναπαραγωγής διαφορετικών καταστάσεων σε όλα

εύρος αλλαγών στις συνθήκες και τις παραμέτρους·

4) η πολυπλοκότητα της ανάπτυξης πρέπει να είναι αποδεκτή για την υπάρχουσα

χρόνο και λογισμικό.

Πρίπλασμαείναι η διαδικασία κατασκευής ενός μοντέλου ενός αντικειμένου και μελέτης των ιδιοτήτων του με την εξέταση του μοντέλου.

Έτσι, η μοντελοποίηση περιλαμβάνει 2 κύρια στάδια:

1) ανάπτυξη μοντέλου.

2) μελέτη του μοντέλου και εξαγωγή συμπερασμάτων.

Ταυτόχρονα, σε κάθε στάδιο επιλύονται διαφορετικές εργασίες και

ουσιαστικά διαφορετικές μέθοδοι και μέσα.

Στην πράξη, χρησιμοποιούνται διάφορες μέθοδοι μοντελοποίησης. Ανάλογα με τη μέθοδο υλοποίησης, όλα τα μοντέλα μπορούν να χωριστούν σε δύο μεγάλες κατηγορίες: φυσικά και μαθηματικά.

Μαθηματική μοντελοποίησηΣυνήθως θεωρείται ως μέσο μελέτης διαδικασιών ή φαινομένων χρησιμοποιώντας τα μαθηματικά τους μοντέλα.

Κάτω από φυσική μοντελοποίησηαναφέρεται στη μελέτη αντικειμένων και φαινομένων σε φυσικά μοντέλα, όταν η διαδικασία που μελετάται αναπαράγεται διατηρώντας τη φυσική της φύση ή χρησιμοποιείται άλλο φυσικό φαινόμενο παρόμοιο με αυτό που μελετάται. Εν φυσικά μοντέλαΚατά κανόνα, υποθέτουν την πραγματική ενσωμάτωση εκείνων των φυσικών ιδιοτήτων του πρωτοτύπου που είναι σημαντικές σε μια συγκεκριμένη κατάσταση.Για παράδειγμα, κατά το σχεδιασμό ενός νέου αεροσκάφους, δημιουργείται μια μακέτα που έχει τις ίδιες αεροδυναμικές ιδιότητες. Όταν σχεδιάζουν μια ανάπτυξη, οι αρχιτέκτονες κατασκευάζουν ένα μοντέλο που αντανακλά τη χωρική διάταξη των στοιχείων του. Από αυτή την άποψη, ονομάζεται επίσης φυσική μοντελοποίηση πρωτότυπο.

Μοντελοποίηση ημιζωήςείναι μια μελέτη ελεγχόμενων συστημάτων σε συγκροτήματα μοντελοποίησης με τη συμπερίληψη πραγματικού εξοπλισμού στο μοντέλο. Μαζί με τον πραγματικό εξοπλισμό, το κλειστό μοντέλο περιλαμβάνει προσομοιωτές επιρροών και παρεμβολών, μαθηματικά μοντέλα του εξωτερικού περιβάλλοντος και διαδικασίες για τις οποίες είναι άγνωστη μια αρκετά ακριβής μαθηματική περιγραφή. Η συμπερίληψη πραγματικού εξοπλισμού ή πραγματικών συστημάτων στο κύκλωμα μοντελοποίησης πολύπλοκων διαδικασιών καθιστά δυνατή τη μείωση της εκ των προτέρων αβεβαιότητας και τη διερεύνηση διαδικασιών για τις οποίες δεν υπάρχει ακριβής μαθηματική περιγραφή. Χρησιμοποιώντας ημι-φυσική μοντελοποίηση, η έρευνα πραγματοποιείται λαμβάνοντας υπόψη μικρές χρονικές σταθερές και γραμμικότητες που είναι εγγενείς στον πραγματικό εξοπλισμό. Κατά τη μελέτη μοντέλων που χρησιμοποιούν πραγματικό εξοπλισμό, χρησιμοποιείται η έννοια δυναμική προσομοίωση, κατά τη μελέτη πολύπλοκων συστημάτων και φαινομένων - εξελικτική, μίμησηΚαι κυβερνητική μοντελοποίηση.

Προφανώς, το πραγματικό όφελος της μοντελοποίησης μπορεί να επιτευχθεί μόνο εάν πληρούνται δύο προϋποθέσεις:

1) το μοντέλο παρέχει σωστή (επαρκή) απεικόνιση των ιδιοτήτων

το πρωτότυπο, σημαντικό από την άποψη της υπό μελέτη λειτουργίας·

2) το μοντέλο σάς επιτρέπει να εξαλείψετε τα εγγενή προβλήματα που αναφέρονται παραπάνω

διεξαγωγή έρευνας σε πραγματικά αντικείμενα.

2. Βασικές έννοιες της μαθηματικής μοντελοποίησης

Η επίλυση πρακτικών προβλημάτων με χρήση μαθηματικών μεθόδων πραγματοποιείται με συνέπεια με τη διατύπωση του προβλήματος (ανάπτυξη μαθηματικού μοντέλου), την επιλογή μιας μεθόδου για τη μελέτη του προκύπτοντος μαθηματικού μοντέλου και την ανάλυση του ληφθέντος μαθηματικού αποτελέσματος. Η μαθηματική διατύπωση του προβλήματος παρουσιάζεται συνήθως με τη μορφή γεωμετρικών εικόνων, συναρτήσεων, συστημάτων εξισώσεων κ.λπ. Η περιγραφή ενός αντικειμένου (φαινομένου) μπορεί να αναπαρασταθεί χρησιμοποιώντας συνεχείς ή διακριτές, ντετερμινιστικές ή στοχαστικές και άλλες μαθηματικές μορφές.

Θεωρία μαθηματικής μοντελοποίησηςεξασφαλίζει τον εντοπισμό προτύπων εμφάνισης διαφόρων φαινομένων στον περιβάλλοντα κόσμο ή τη λειτουργία συστημάτων και συσκευών μέσω της μαθηματικής περιγραφής και μοντελοποίησής τους χωρίς τη διενέργεια δοκιμών πλήρους κλίμακας. Σε αυτή την περίπτωση, χρησιμοποιούνται οι διατάξεις και οι νόμοι των μαθηματικών που περιγράφουν τα προσομοιωμένα φαινόμενα, συστήματα ή συσκευές σε κάποιο επίπεδο εξιδανίκευσης τους.

Μαθηματικό μοντέλο (MM)είναι μια τυπική περιγραφή ενός συστήματος (ή λειτουργίας) σε κάποια αφηρημένη γλώσσα, για παράδειγμα, με τη μορφή ενός συνόλου μαθηματικών σχέσεων ή ενός διαγράμματος αλγορίθμου, π.χ. δηλ. μια τέτοια μαθηματική περιγραφή που παρέχει προσομοίωση της λειτουργίας συστημάτων ή συσκευών σε επίπεδο αρκετά κοντά στην πραγματική τους συμπεριφορά που προκύπτει κατά τη διάρκεια δοκιμών πλήρους κλίμακας συστημάτων ή συσκευών.

Οποιοδήποτε ΜΜ περιγράφει ένα πραγματικό αντικείμενο, φαινόμενο ή διαδικασία με κάποιο βαθμό προσέγγισης στην πραγματικότητα. Ο τύπος του ΜΜ εξαρτάται τόσο από τη φύση του πραγματικού αντικειμένου όσο και από τους στόχους της μελέτης.

Μαθηματική μοντελοποίησηκοινωνικά, οικονομικά, βιολογικά και φυσικά φαινόμενα, αντικείμενα, συστήματα και διάφορες συσκευές είναι ένα από τα πιο σημαντικά μέσα κατανόησης της φύσης και σχεδιασμού μιας μεγάλης ποικιλίας συστημάτων και συσκευών. Υπάρχουν γνωστά παραδείγματα αποτελεσματικής χρήσης μοντελοποίησης στη δημιουργία πυρηνικών τεχνολογιών, αεροπορικών και αεροδιαστημικών συστημάτων, στην πρόβλεψη ατμοσφαιρικών και ωκεανικών φαινομένων, καιρού κ.λπ.

Ωστόσο, τέτοιοι σοβαροί τομείς μοντελοποίησης απαιτούν συχνά υπερυπολογιστές και χρόνια εργασίας από μεγάλες ομάδες επιστημόνων για την προετοιμασία δεδομένων για τη μοντελοποίηση και τον εντοπισμό σφαλμάτων. Ωστόσο, σε αυτήν την περίπτωση, η μαθηματική μοντελοποίηση πολύπλοκων συστημάτων και συσκευών όχι μόνο εξοικονομεί χρήματα για έρευνα και δοκιμές, αλλά μπορεί επίσης να εξαλείψει περιβαλλοντικές καταστροφές - για παράδειγμα, σας επιτρέπει να εγκαταλείψετε τη δοκιμή πυρηνικών και θερμοπυρηνικών όπλων υπέρ της μαθηματικής τους μοντελοποίησης ή δοκιμή αεροδιαστημικών συστημάτων πριν από τις πραγματικές πτήσεις τους. Μεταξύ Επομένως, η μαθηματική μοντελοποίηση σε επίπεδο επίλυσης απλούστερων προβλημάτων, για παράδειγμα, από τον τομέα της μηχανικής, της ηλεκτρολογικής μηχανικής, της ηλεκτρονικής, της ραδιομηχανικής και πολλών άλλων τομέων της επιστήμης και της τεχνολογίας έχει πλέον γίνει διαθέσιμο για εκτέλεση σε σύγχρονους υπολογιστές. Και όταν χρησιμοποιούνται γενικευμένα μοντέλα, καθίσταται δυνατή η προσομοίωση αρκετά περίπλοκων συστημάτων, για παράδειγμα, συστήματα και δίκτυα τηλεπικοινωνιών, συστήματα ραδιοπλοήγησης ραντάρ ή ραδιοπλοήγησης.

Ο σκοπός της μαθηματικής μοντελοποίησηςείναι η ανάλυση πραγματικών διεργασιών (στη φύση ή την τεχνολογία) με τη χρήση μαθηματικών μεθόδων. Με τη σειρά του, αυτό απαιτεί να μελετηθεί η τυποποίηση της διαδικασίας MM. Το μοντέλο μπορεί να είναι μια μαθηματική έκφραση που περιέχει μεταβλητές των οποίων η συμπεριφορά είναι παρόμοια με τη συμπεριφορά ενός πραγματικού συστήματος. Το μοντέλο μπορεί να περιλαμβάνει στοιχεία τυχαίας που λαμβάνουν υπόψη τις πιθανότητες πιθανές ενέργειες δύο ή περισσότερων «παικτών», όπως, για παράδειγμα, στα θεωρητικά παιχνίδια. ή μπορεί να αντιπροσωπεύει πραγματικές μεταβλητές διασυνδεδεμένων τμημάτων του λειτουργικού συστήματος.

Η μαθηματική μοντελοποίηση για τη μελέτη των χαρακτηριστικών συστημάτων μπορεί να χωριστεί σε αναλυτική, προσομοίωση και συνδυαστική. Με τη σειρά τους, τα MM χωρίζονται σε προσομοίωση και αναλυτικά.

Αναλυτική Μοντελοποίηση

Για αναλυτική μοντελοποίησηΕίναι χαρακτηριστικό ότι οι διαδικασίες της λειτουργίας του συστήματος γράφονται με τη μορφή ορισμένων συναρτησιακών σχέσεων (αλγεβρικές, διαφορικές, ολοκληρωτικές εξισώσεις). Το αναλυτικό μοντέλο μπορεί να μελετηθεί χρησιμοποιώντας τις ακόλουθες μεθόδους:

1) αναλυτικά, όταν προσπαθούν να αποκτήσουν, σε γενική μορφή, ρητές εξαρτήσεις για τα χαρακτηριστικά των συστημάτων.

2) αριθμητική, όταν δεν είναι δυνατή η εύρεση λύσης στις εξισώσεις σε γενική μορφή και λύνονται για συγκεκριμένα αρχικά δεδομένα.

3) ποιοτικό, όταν ελλείψει λύσης βρίσκονται κάποιες από τις ιδιότητές του.

Αναλυτικά μοντέλα μπορούν να ληφθούν μόνο για σχετικά απλά συστήματα. Για πολύπλοκα συστήματα, συχνά προκύπτουν μεγάλα μαθηματικά προβλήματα. Για να εφαρμόσουν την αναλυτική μέθοδο, προχωρούν σε σημαντική απλοποίηση του αρχικού μοντέλου. Ωστόσο, η έρευνα που χρησιμοποιεί ένα απλοποιημένο μοντέλο βοηθά στην απόκτηση μόνο ενδεικτικών αποτελεσμάτων. Τα αναλυτικά μοντέλα αντικατοπτρίζουν σωστά μαθηματικά τη σχέση μεταξύ των μεταβλητών και των παραμέτρων εισόδου και εξόδου. Αλλά η δομή τους δεν αντανακλά την εσωτερική δομή του αντικειμένου.

Κατά τη διάρκεια της αναλυτικής μοντελοποίησης, τα αποτελέσματά της παρουσιάζονται με τη μορφή αναλυτικών εκφράσεων. Για παράδειγμα, με τη σύνδεση R.C.- κύκλωμα σε πηγή σταθερής τάσης μι(R, ντοΚαι μι- συστατικά αυτού του μοντέλου), μπορούμε να δημιουργήσουμε μια αναλυτική έκφραση για τη χρονική εξάρτηση της τάσης u(t) στον πυκνωτή ντο:

Αυτή η γραμμική διαφορική εξίσωση (DE) είναι το αναλυτικό μοντέλο αυτού του απλού γραμμικού κυκλώματος. Η αναλυτική του λύση, υπό την αρχική συνθήκη u(0) = 0, που σημαίνει έναν αποφορτισμένο πυκνωτή ντοστην αρχή της μοντελοποίησης, σας επιτρέπει να βρείτε την επιθυμητή εξάρτηση - με τη μορφή ενός τύπου:

u(t) = μι(1− πρώηνΠ(- t/RC)). (2)

Ωστόσο, ακόμη και σε αυτό το απλούστερο παράδειγμα, απαιτούνται ορισμένες προσπάθειες για την επίλυση του DE (1) ή για την εφαρμογή συστήματα μαθηματικών υπολογιστών(SCM) με συμβολικούς υπολογισμούς – υπολογιστικά συστήματα άλγεβρας. Για αυτήν την εντελώς ασήμαντη περίπτωση, η επίλυση του προβλήματος της μοντελοποίησης μιας γραμμικής R.C.-το κύκλωμα δίνει αναλυτική έκφραση (2) μιας αρκετά γενικής μορφής - είναι κατάλληλο για την περιγραφή της λειτουργίας του κυκλώματος για οποιεσδήποτε ονομασίες εξαρτημάτων R, ντοΚαι μι, και περιγράφει το εκθετικό φορτίο του πυκνωτή ντομέσω μιας αντίστασης Rαπό πηγή σταθερής τάσης μι.

Φυσικά, η εύρεση αναλυτικών λύσεων κατά τη διάρκεια της αναλυτικής μοντελοποίησης αποδεικνύεται εξαιρετικά πολύτιμη για τον εντοπισμό γενικών θεωρητικών μοτίβων απλών γραμμικών κυκλωμάτων, συστημάτων και συσκευών. Ωστόσο, η πολυπλοκότητά της αυξάνεται απότομα καθώς οι επιρροές στο μοντέλο γίνονται πιο περίπλοκες και η σειρά και ο αριθμός των οι εξισώσεις καταστάσεων που περιγράφουν το μοντελοποιημένο αντικείμενο αυξάνονται. Μπορείτε να έχετε περισσότερο ή λιγότερο ορατά αποτελέσματα κατά τη μοντελοποίηση αντικειμένων δεύτερης ή τρίτης τάξης, αλλά με υψηλότερη τάξη, οι αναλυτικές εκφράσεις γίνονται υπερβολικά περίπλοκες, περίπλοκες και δυσνόητες. Για παράδειγμα, ακόμη και ένας απλός ηλεκτρονικός ενισχυτής περιέχει συχνά δεκάδες εξαρτήματα. Ωστόσο, πολλά σύγχρονα SCMs, για παράδειγμα, συστήματα συμβολικών μαθηματικών Maple, Mathematicaή περιβάλλον MATLAB, είναι ικανά να αυτοματοποιήσουν σε μεγάλο βαθμό την επίλυση σύνθετων προβλημάτων αναλυτικής μοντελοποίησης.

Ένας τύπος μοντελοποίησης είναι αριθμητική μοντελοποίηση,που συνίσταται στη λήψη των απαραίτητων ποσοτικών δεδομένων για τη συμπεριφορά συστημάτων ή συσκευών με οποιαδήποτε κατάλληλη αριθμητική μέθοδο, όπως οι μέθοδοι Euler ή Runge-Kutta. Στην πράξη, η μοντελοποίηση μη γραμμικών συστημάτων και συσκευών με χρήση αριθμητικών μεθόδων αποδεικνύεται πολύ πιο αποτελεσματική από την αναλυτική μοντελοποίηση μεμονωμένων ιδιωτικών γραμμικών κυκλωμάτων, συστημάτων ή συσκευών. Για παράδειγμα, για την επίλυση συστημάτων DE (1) ή DE σε πιο περίπλοκες περιπτώσεις, δεν μπορεί να ληφθεί μια λύση σε αναλυτική μορφή, αλλά χρησιμοποιώντας αριθμητικά δεδομένα προσομοίωσης, μπορείτε να λάβετε αρκετά πλήρη δεδομένα σχετικά με τη συμπεριφορά των προσομοιωμένων συστημάτων και συσκευών. ως κατασκευή γραφημάτων εξαρτήσεων που περιγράφουν αυτή τη συμπεριφορά.

Μοντελοποίηση προσομοίωσης

Στο μίμηση 10 και μοντελοποίηση, ο αλγόριθμος που υλοποιεί το μοντέλο αναπαράγει τη διαδικασία λειτουργίας του συστήματος με την πάροδο του χρόνου. Τα στοιχειώδη φαινόμενα που συνθέτουν τη διαδικασία προσομοιώνονται, διατηρώντας τη λογική τους δομή και την αλληλουχία των γεγονότων στο χρόνο.

Το κύριο πλεονέκτημα των μοντέλων προσομοίωσης σε σύγκριση με τα αναλυτικά είναι η ικανότητα επίλυσης πιο περίπλοκων προβλημάτων.

Τα μοντέλα προσομοίωσης καθιστούν εύκολο να ληφθεί υπόψη η παρουσία διακριτών ή συνεχών στοιχείων, μη γραμμικών χαρακτηριστικών, τυχαίων επιρροών κ.λπ. Επομένως, αυτή η μέθοδος χρησιμοποιείται ευρέως στο στάδιο σχεδιασμού πολύπλοκων συστημάτων. Το κύριο μέσο υλοποίησης της μοντελοποίησης προσομοίωσης είναι ένας υπολογιστής, ο οποίος επιτρέπει την ψηφιακή μοντελοποίηση συστημάτων και σημάτων.

Από αυτή την άποψη, ας ορίσουμε τη φράση « μοντελοποίηση υπολογιστή», που χρησιμοποιείται όλο και περισσότερο στη βιβλιογραφία. Ας υποθέσουμε ότι μοντελοποίηση υπολογιστήείναι η μαθηματική μοντελοποίηση με χρήση τεχνολογίας υπολογιστών. Κατά συνέπεια, η τεχνολογία μοντελοποίησης υπολογιστή περιλαμβάνει την εκτέλεση των ακόλουθων ενεργειών:

1) προσδιορισμός του σκοπού της μοντελοποίησης.

2) ανάπτυξη ενός εννοιολογικού μοντέλου.

3) επισημοποίηση του μοντέλου.

4) εφαρμογή λογισμικού του μοντέλου?

5) προγραμματισμός πειραμάτων μοντέλου.

6) υλοποίηση του πειραματικού σχεδίου.

7) ανάλυση και ερμηνεία των αποτελεσμάτων μοντελοποίησης.

Στο μοντελοποίηση προσομοίωσηςτο MM που χρησιμοποιείται αναπαράγει τον αλγόριθμο ("λογική") της λειτουργίας του υπό μελέτη συστήματος με την πάροδο του χρόνου για διάφορους συνδυασμούς τιμών των παραμέτρων του συστήματος και του εξωτερικού περιβάλλοντος.

Ένα παράδειγμα του απλούστερου αναλυτικού μοντέλου είναι η εξίσωση της ευθύγραμμης ομοιόμορφης κίνησης. Κατά τη μελέτη μιας τέτοιας διαδικασίας χρησιμοποιώντας ένα μοντέλο προσομοίωσης, θα πρέπει να εφαρμοστεί η παρατήρηση των αλλαγών στη διαδρομή που διανύθηκε με την πάροδο του χρόνου Προφανώς, σε ορισμένες περιπτώσεις προτιμάται περισσότερο η αναλυτική μοντελοποίηση, σε άλλες - η προσομοίωση (ή συνδυασμός και των δύο). Για να κάνετε μια επιτυχημένη επιλογή, πρέπει να απαντήσετε σε δύο ερωτήσεις.

Ποιος είναι ο σκοπός του μόντελινγκ;

Σε ποια τάξη μπορεί να ταξινομηθεί το μοντελοποιημένο φαινόμενο;

Απαντήσεις και στις δύο αυτές ερωτήσεις μπορούν να ληφθούν κατά τα δύο πρώτα στάδια της μοντελοποίησης.

Τα μοντέλα προσομοίωσης όχι μόνο σε ιδιότητες, αλλά και στη δομή αντιστοιχούν στο μοντελοποιημένο αντικείμενο. Σε αυτή την περίπτωση, υπάρχει μια σαφής και προφανής αντιστοιχία μεταξύ των διεργασιών που λαμβάνονται στο μοντέλο και των διεργασιών που συμβαίνουν στο αντικείμενο. Το μειονέκτημα της προσομοίωσης είναι ότι χρειάζεται πολύς χρόνος για να λυθεί το πρόβλημα για να επιτευχθεί καλή ακρίβεια.

Τα αποτελέσματα της μοντελοποίησης προσομοίωσης της λειτουργίας ενός στοχαστικού συστήματος είναι πραγματοποιήσεις τυχαίων μεταβλητών ή διεργασιών. Επομένως, για να βρεθούν τα χαρακτηριστικά του συστήματος, απαιτούνται πολλαπλές επαναλήψεις και επακόλουθη επεξεργασία δεδομένων. Τις περισσότερες φορές σε αυτή την περίπτωση, χρησιμοποιείται ένας τύπος προσομοίωσης - στατιστικός

πρίπλασμα(ή μέθοδος Monte Carlo), δηλ. αναπαραγωγή τυχαίων παραγόντων, γεγονότων, ποσοτήτων, διεργασιών, πεδίων σε μοντέλα.

Με βάση τα αποτελέσματα της στατιστικής μοντελοποίησης, προσδιορίζονται εκτιμήσεις πιθανοτικών κριτηρίων ποιότητας, γενικών και ειδικών, που χαρακτηρίζουν τη λειτουργία και την αποτελεσματικότητα του διαχειριζόμενου συστήματος. Η στατιστική μοντελοποίηση χρησιμοποιείται ευρέως για την επίλυση επιστημονικών και εφαρμοσμένων προβλημάτων σε διάφορους τομείς της επιστήμης και της τεχνολογίας. Οι μέθοδοι στατιστικής μοντελοποίησης χρησιμοποιούνται ευρέως στη μελέτη πολύπλοκων δυναμικών συστημάτων, αξιολογώντας τη λειτουργία και την αποτελεσματικότητά τους.

Το τελικό στάδιο της στατιστικής μοντελοποίησης βασίζεται στη μαθηματική επεξεργασία των αποτελεσμάτων που προκύπτουν. Εδώ χρησιμοποιούνται μέθοδοι μαθηματικής στατιστικής (παραμετρική και μη παραμετρική εκτίμηση, έλεγχος υποθέσεων). Ένα παράδειγμα παραμετρικού εκτιμητή είναι ο μέσος όρος του δείγματος ενός μέτρου απόδοσης. Μεταξύ των μη παραμετρικών μεθόδων, ευρέως διαδεδομένη μέθοδος ιστογράμματος.

Το εξεταζόμενο σχήμα βασίζεται σε επαναλαμβανόμενες στατιστικές δοκιμές του συστήματος και μεθόδους στατιστικής ανεξάρτητων τυχαίων μεταβλητών.Το σχήμα αυτό δεν είναι πάντα φυσικό στην πράξη και βέλτιστο από άποψη κόστους. Η μείωση του χρόνου δοκιμής του συστήματος μπορεί να επιτευχθεί με τη χρήση πιο ακριβών μεθόδων αξιολόγησης. Όπως είναι γνωστό από τις μαθηματικές στατιστικές, οι αποτελεσματικές εκτιμήσεις έχουν τη μεγαλύτερη ακρίβεια για ένα δεδομένο μέγεθος δείγματος. Το βέλτιστο φιλτράρισμα και η μέθοδος μέγιστης πιθανότητας παρέχουν μια γενική μέθοδο για τη λήψη τέτοιων εκτιμήσεων.Στα προβλήματα στατιστικής μοντελοποίησης, οι εφαρμογές επεξεργασίας τυχαίων διεργασιών είναι απαραίτητες όχι μόνο για την ανάλυση διεργασιών εξόδου.

Ο έλεγχος των χαρακτηριστικών των τυχαίων επιρροών εισόδου είναι επίσης πολύ σημαντικός. Ο έλεγχος συνίσταται στον έλεγχο της συμμόρφωσης των κατανομών των δημιουργούμενων διαδικασιών με τις δεδομένες κατανομές. Αυτό το πρόβλημα συχνά διατυπώνεται ως πρόβλημα ελέγχου υποθέσεων.

Η γενική τάση στην υπολογιστική μοντελοποίηση σύνθετων ελεγχόμενων συστημάτων είναι η επιθυμία μείωσης του χρόνου μοντελοποίησης, καθώς και η διεξαγωγή έρευνας σε πραγματικό χρόνο. Είναι βολικό να αναπαραστούμε υπολογιστικούς αλγόριθμους σε επαναλαμβανόμενη μορφή, επιτρέποντας την εφαρμογή τους με το ρυθμό λήψης της τρέχουσας πληροφορίας.

ΑΡΧΕΣ ΜΙΑΣ ΣΥΣΤΗΜΑΤΙΚΗΣ ΠΡΟΣΕΓΓΙΣΗΣ ΣΤΗ ΜΟΝΤΕΛΕΥΣΗ

Βασικές αρχές της θεωρίας συστημάτων

Οι βασικές αρχές της θεωρίας συστημάτων προέκυψαν κατά τη μελέτη των δυναμικών συστημάτων και των λειτουργικών τους στοιχείων. Ένα σύστημα νοείται ως μια ομάδα διασυνδεδεμένων στοιχείων που ενεργούν μαζί για να ολοκληρώσουν μια προκαθορισμένη εργασία. Η ανάλυση συστημάτων μας επιτρέπει να προσδιορίσουμε τους πιο ρεαλιστικούς τρόπους εκτέλεσης μιας δεδομένης εργασίας, διασφαλίζοντας τη μέγιστη ικανοποίηση των αναφερόμενων απαιτήσεων.

Τα στοιχεία που αποτελούν τη βάση της θεωρίας συστημάτων δεν δημιουργούνται μέσω υποθέσεων, αλλά ανακαλύπτονται πειραματικά. Για να ξεκινήσει η κατασκευή ενός συστήματος, είναι απαραίτητο να υπάρχουν γενικά χαρακτηριστικά των τεχνολογικών διαδικασιών. Το ίδιο ισχύει και όσον αφορά τις αρχές δημιουργίας μαθηματικά διατυπωμένων κριτηρίων που πρέπει να ικανοποιεί μια διαδικασία ή η θεωρητική περιγραφή της. Η μοντελοποίηση είναι μια από τις σημαντικότερες μεθόδους επιστημονικής έρευνας και πειραματισμού.

Κατά την κατασκευή μοντέλων αντικειμένων, χρησιμοποιείται μια προσέγγιση συστημάτων, η οποία είναι μια μεθοδολογία για την επίλυση πολύπλοκων προβλημάτων, η οποία βασίζεται στην εξέταση του αντικειμένου ως συστήματος που λειτουργεί σε ένα συγκεκριμένο περιβάλλον. Μια συστηματική προσέγγιση περιλαμβάνει την αποκάλυψη της ακεραιότητας ενός αντικειμένου, τον εντοπισμό και τη μελέτη της εσωτερικής δομής του, καθώς και τις συνδέσεις με το εξωτερικό περιβάλλον. Σε αυτή την περίπτωση, το αντικείμενο παρουσιάζεται ως μέρος του πραγματικού κόσμου, το οποίο απομονώνεται και μελετάται σε σχέση με το πρόβλημα της κατασκευής ενός μοντέλου. Επιπλέον, η συστημική προσέγγιση περιλαμβάνει μια συνεπή μετάβαση από το γενικό στο ειδικό, όταν ο στόχος του σχεδιασμού είναι η βάση της εξέτασης και το αντικείμενο εξετάζεται σε σχέση με το περιβάλλον.

Ένα σύνθετο αντικείμενο μπορεί να χωριστεί σε υποσυστήματα, τα οποία είναι μέρη του αντικειμένου που πληρούν τις ακόλουθες απαιτήσεις:

1) ένα υποσύστημα είναι ένα λειτουργικά ανεξάρτητο μέρος ενός αντικειμένου. Συνδέεται με άλλα υποσυστήματα, ανταλλάσσει πληροφορίες και ενέργεια μαζί τους.

2) για κάθε υποσύστημα μπορούν να οριστούν συναρτήσεις ή ιδιότητες που δεν συμπίπτουν με τις ιδιότητες ολόκληρου του συστήματος.

3) καθένα από τα υποσυστήματα μπορεί να υποβληθεί σε περαιτέρω διαίρεση στο επίπεδο των στοιχείων.

Στην περίπτωση αυτή, ένα στοιχείο νοείται ως ένα υποσύστημα χαμηλότερου επιπέδου, η περαιτέρω διαίρεση του οποίου είναι ακατάλληλη από τη σκοπιά του προβλήματος που επιλύεται.

Έτσι, ένα σύστημα μπορεί να οριστεί ως μια αναπαράσταση ενός αντικειμένου με τη μορφή ενός συνόλου υποσυστημάτων, στοιχείων και συνδέσεων με σκοπό τη δημιουργία, την έρευνα ή τη βελτίωσή του. Σε αυτήν την περίπτωση, μια διευρυμένη αναπαράσταση του συστήματος, συμπεριλαμβανομένων των κύριων υποσυστημάτων και των συνδέσεων μεταξύ τους, ονομάζεται μακροδομή και μια λεπτομερής αποκάλυψη της εσωτερικής δομής του συστήματος μέχρι το επίπεδο των στοιχείων ονομάζεται μικροδομή.

Μαζί με το σύστημα, υπάρχει συνήθως ένα υπερσύστημα - ένα σύστημα υψηλότερου επιπέδου, το οποίο περιλαμβάνει το εν λόγω αντικείμενο και η λειτουργία οποιουδήποτε συστήματος μπορεί να προσδιοριστεί μόνο μέσω του υπερσυστήματος.

Είναι απαραίτητο να τονιστεί η έννοια του περιβάλλοντος ως ενός συνόλου αντικειμένων του εξωτερικού κόσμου που επηρεάζουν σημαντικά την αποτελεσματικότητα του συστήματος, αλλά δεν αποτελούν μέρος του συστήματος και του υπερσύστημά του.

Σε σχέση με τη συστημική προσέγγιση των μοντέλων κτιρίων, χρησιμοποιείται η έννοια της υποδομής, η οποία περιγράφει τη σχέση του συστήματος με το περιβάλλον του (περιβάλλον) Στην περίπτωση αυτή, ο προσδιορισμός, η περιγραφή και η μελέτη των ιδιοτήτων ενός αντικειμένου που είναι απαραίτητες. μέσα στο πλαίσιο μιας συγκεκριμένης εργασίας ονομάζεται διαστρωμάτωση του αντικειμένου και οποιοδήποτε μοντέλο του αντικειμένου είναι η στρωματοποιημένη περιγραφή του.

Για μια συστημική προσέγγιση, είναι σημαντικό να προσδιοριστεί η δομή του συστήματος, δηλ. ένα σύνολο συνδέσεων μεταξύ στοιχείων του συστήματος, που αντικατοπτρίζουν την αλληλεπίδρασή τους. Για να γίνει αυτό, εξετάζουμε πρώτα τις δομικές και λειτουργικές προσεγγίσεις στη μοντελοποίηση.

Με μια δομική προσέγγιση, αποκαλύπτεται η σύνθεση των επιλεγμένων στοιχείων του συστήματος και οι μεταξύ τους συνδέσεις. Το σύνολο των στοιχείων και των συνδέσεων μας επιτρέπει να κρίνουμε τη δομή του συστήματος. Η πιο γενική περιγραφή μιας δομής είναι μια τοπολογική περιγραφή. Σας επιτρέπει να προσδιορίσετε τα στοιχεία του συστήματος και τις συνδέσεις τους χρησιμοποιώντας γραφήματα. Λιγότερο γενική είναι η περιγραφή της λειτουργίας, όταν εξετάζονται μεμονωμένες συναρτήσεις, δηλαδή αλγόριθμοι για τη συμπεριφορά του συστήματος. Σε αυτή την περίπτωση, εφαρμόζεται μια λειτουργική προσέγγιση που ορίζει τις λειτουργίες που εκτελεί το σύστημα.

Με βάση τη συστημική προσέγγιση, μπορεί να προταθεί μια ακολουθία ανάπτυξης μοντέλου, όταν διακρίνονται δύο κύρια στάδια σχεδιασμού: ο μακροσχεδιασμός και ο μικροσχεδιασμός.

Στο στάδιο του μακροσχεδιασμού, δημιουργείται ένα μοντέλο του εξωτερικού περιβάλλοντος, εντοπίζονται πόροι και περιορισμοί, επιλέγεται ένα μοντέλο συστήματος και κριτήρια για την αξιολόγηση της επάρκειας.

Το στάδιο μικροσχεδίασης εξαρτάται σε μεγάλο βαθμό από τον συγκεκριμένο τύπο μοντέλου που επιλέγεται. Γενικά, περιλαμβάνει τη δημιουργία πληροφοριακών, μαθηματικών, τεχνικών και λογισμικών συστημάτων μοντελοποίησης. Σε αυτό το στάδιο, καθορίζονται τα κύρια τεχνικά χαρακτηριστικά του δημιουργημένου μοντέλου, εκτιμάται ο χρόνος που απαιτείται για την εργασία με αυτό και το κόστος των πόρων για την απόκτηση της καθορισμένης ποιότητας του μοντέλου.

Ανεξάρτητα από τον τύπο του μοντέλου, κατά την κατασκευή του, είναι απαραίτητο να καθοδηγείται από μια σειρά από αρχές μιας συστηματικής προσέγγισης:

1) συνεπής εξέλιξη στα στάδια δημιουργίας ενός μοντέλου.

2) συντονισμός πληροφοριών, πόρων, αξιοπιστίας και άλλων χαρακτηριστικών.

3) τη σωστή σχέση μεταξύ των διαφορετικών επιπέδων κατασκευής μοντέλου.

4) την ακεραιότητα των επιμέρους σταδίων του σχεδιασμού του μοντέλου.

Για να δημιουργήσετε ένα μαθηματικό μοντέλο χρειάζεστε:

να αναλύσει προσεκτικά ένα πραγματικό αντικείμενο ή διαδικασία.
επισημάνετε τα πιο σημαντικά χαρακτηριστικά και ιδιότητές του·
ορίζει μεταβλητές, δηλ. παραμέτρους των οποίων οι τιμές επηρεάζουν τα κύρια χαρακτηριστικά και ιδιότητες του αντικειμένου.
περιγράφουν την εξάρτηση των βασικών ιδιοτήτων ενός αντικειμένου, διεργασίας ή συστήματος από τις τιμές των μεταβλητών χρησιμοποιώντας λογικομαθηματικές σχέσεις (εξισώσεις, ισότητες, ανισότητες, λογικομαθηματικές κατασκευές).
επισημάνετε τις εσωτερικές συνδέσεις ενός αντικειμένου, διεργασίας ή συστήματος χρησιμοποιώντας περιορισμούς, εξισώσεις, ισότητες, ανισότητες, λογικές και μαθηματικές κατασκευές.
να εντοπίσετε εξωτερικές συνδέσεις και να τις περιγράψετε χρησιμοποιώντας περιορισμούς, εξισώσεις, ισότητες, ανισότητες, λογικές και μαθηματικές κατασκευές.

Η μαθηματική μοντελοποίηση, εκτός από τη μελέτη ενός αντικειμένου, διεργασίας ή συστήματος και τη σύνταξη μιας μαθηματικής περιγραφής του, περιλαμβάνει επίσης:

κατασκευή ενός αλγορίθμου που μοντελοποιεί τη συμπεριφορά ενός αντικειμένου, διαδικασίας ή συστήματος.
έλεγχος της επάρκειας του μοντέλου και του αντικειμένου, της διαδικασίας ή του συστήματος με βάση υπολογιστικά και πλήρους κλίμακας πειράματα·
προσαρμογή μοντέλου?
χρησιμοποιώντας το μοντέλο.

Η μαθηματική περιγραφή των υπό μελέτη διεργασιών και συστημάτων εξαρτάται από:

τη φύση μιας πραγματικής διαδικασίας ή συστήματος και συντάσσεται με βάση τους νόμους της φυσικής, της χημείας, της μηχανικής, της θερμοδυναμικής, της υδροδυναμικής, της ηλεκτρικής μηχανικής, της θεωρίας πλαστικότητας, της θεωρίας ελαστικότητας κ.λπ.
την απαιτούμενη αξιοπιστία και ακρίβεια της μελέτης και της έρευνας πραγματικών διαδικασιών και συστημάτων.

Η κατασκευή ενός μαθηματικού μοντέλου ξεκινά συνήθως με την κατασκευή και ανάλυση του απλούστερου, πιο χονδροειδούς μαθηματικού μοντέλου του υπό εξέταση αντικειμένου, διαδικασίας ή συστήματος. Στο μέλλον, εάν χρειαστεί, το μοντέλο τελειοποιείται και η αντιστοιχία του με το αντικείμενο γίνεται πιο ολοκληρωμένη.

Ας πάρουμε ένα απλό παράδειγμα. Είναι απαραίτητο να προσδιοριστεί η επιφάνεια του γραφείου. Συνήθως, αυτό γίνεται μετρώντας το μήκος και το πλάτος του και, στη συνέχεια, πολλαπλασιάζοντας τους αριθμούς που προκύπτουν. Αυτή η στοιχειώδης διαδικασία σημαίνει στην πραγματικότητα το εξής: ένα πραγματικό αντικείμενο (επιφάνεια πίνακα) αντικαθίσταται από ένα αφηρημένο μαθηματικό μοντέλο - ένα ορθογώνιο. Οι διαστάσεις που λαμβάνονται με τη μέτρηση του μήκους και του πλάτους της επιφάνειας του τραπεζιού αντιστοιχίζονται στο ορθογώνιο και η περιοχή ενός τέτοιου ορθογωνίου θεωρείται περίπου η απαιτούμενη περιοχή του τραπεζιού. Ωστόσο, το ορθογώνιο μοντέλο για ένα γραφείο είναι το απλούστερο, πιο ακατέργαστο μοντέλο. Εάν προσεγγίσετε πιο σοβαρά το πρόβλημα, πριν χρησιμοποιήσετε ένα ορθογώνιο μοντέλο για να προσδιορίσετε την περιοχή του πίνακα, αυτό το μοντέλο πρέπει να ελεγχθεί. Οι έλεγχοι μπορούν να πραγματοποιηθούν ως εξής: μετρήστε τα μήκη των απέναντι πλευρών του πίνακα, καθώς και τα μήκη των διαγωνίων του και συγκρίνετε τα μεταξύ τους. Εάν, με τον απαιτούμενο βαθμό ακρίβειας, τα μήκη των απέναντι πλευρών και τα μήκη των διαγωνίων είναι ίσα σε ζεύγη, τότε η επιφάνεια του τραπεζιού μπορεί πραγματικά να θεωρηθεί ως ορθογώνιο. Διαφορετικά, το μοντέλο ορθογωνίου θα πρέπει να απορριφθεί και να αντικατασταθεί με ένα γενικό τετράπλευρο μοντέλο. Με μεγαλύτερη απαίτηση ακρίβειας, μπορεί να είναι απαραίτητο να τελειοποιήσετε ακόμη περισσότερο το μοντέλο, για παράδειγμα, ώστε να ληφθεί υπόψη η στρογγυλοποίηση των γωνιών του τραπεζιού.

Χρησιμοποιώντας αυτό το απλό παράδειγμα, αποδείχθηκε ότι το μαθηματικό μοντέλο δεν καθορίζεται μοναδικά από το αντικείμενο, τη διαδικασία ή Σύστημα.

Ή (θα διευκρινιστεί αύριο)

Τρόποι επίλυσης μαθηματικών. Μοντέλα:

1, Κατασκευή μοντέλου με βάση τους νόμους της φύσης (αναλυτική μέθοδος)

2. Ο επίσημος τρόπος με τη χρήση στατιστικών μεθόδων. Αποτελέσματα επεξεργασίας και μέτρησης (στατιστική προσέγγιση)

3. Κατασκευή μοντέλου βασισμένου σε μοντέλο στοιχείων (σύνθετα συστήματα)

1, Αναλυτική - χρήση με επαρκή μελέτη. Το γενικό μοτίβο είναι γνωστό. Μοντέλα.

2. πείραμα. Ελλείψει πληροφοριών.

3. Μίμηση μ. - εξερευνά τις ιδιότητες του αντικειμένου. Γενικά.

Ένα παράδειγμα κατασκευής μαθηματικού μοντέλου.

Μαθηματικό μοντέλοείναι μια μαθηματική αναπαράσταση της πραγματικότητας.

Μαθηματική μοντελοποίησηείναι η διαδικασία κατασκευής και μελέτης μαθηματικών μοντέλων.

Όλες οι φυσικές και κοινωνικές επιστήμες που χρησιμοποιούν τα μαθηματικά ασχολούνται ουσιαστικά με τη μαθηματική μοντελοποίηση: αντικαθιστούν ένα αντικείμενο με το μαθηματικό του μοντέλο και στη συνέχεια μελετούν το τελευταίο. Η σύνδεση μεταξύ ενός μαθηματικού μοντέλου και της πραγματικότητας πραγματοποιείται χρησιμοποιώντας μια αλυσίδα υποθέσεων, εξιδανικεύσεων και απλουστεύσεων. Χρησιμοποιώντας μαθηματικές μεθόδους, κατά κανόνα, περιγράφεται ένα ιδανικό αντικείμενο που κατασκευάστηκε στο στάδιο της ουσιαστικής μοντελοποίησης.

Γιατί χρειάζονται μοντέλα;

Πολύ συχνά, κατά τη μελέτη οποιουδήποτε αντικειμένου, προκύπτουν δυσκολίες. Το ίδιο το πρωτότυπο μερικές φορές δεν είναι διαθέσιμο ή η χρήση του δεν συνιστάται ή η προσέλκυση του πρωτοτύπου είναι ακριβή. Όλα αυτά τα προβλήματα μπορούν να λυθούν χρησιμοποιώντας προσομοίωση. Κατά μια ορισμένη έννοια, ένα μοντέλο μπορεί να αντικαταστήσει το υπό μελέτη αντικείμενο.

Τα πιο απλά παραδείγματα μοντέλων

§ Μια φωτογραφία μπορεί να ονομαστεί μοντέλο ανθρώπου. Για να αναγνωρίσετε ένα άτομο, αρκεί να δείτε τη φωτογραφία του.

§ Ο αρχιτέκτονας δημιούργησε ένα μοντέλο νέας οικιστικής περιοχής. Μπορεί να μετακινήσει ένα πολυώροφο κτίριο από το ένα μέρος στο άλλο με μια κίνηση του χεριού του. Στην πραγματικότητα αυτό δεν θα ήταν δυνατό.

Τύποι μοντέλων

Τα μοντέλα μπορούν να χωριστούν σε υλικό"Και τέλειος. Τα παραπάνω παραδείγματα είναι μοντέλα υλικών. Τα ιδανικά μοντέλα έχουν συχνά εικονικά σχήματα. Οι πραγματικές έννοιες αντικαθίστανται από κάποια σημάδια, τα οποία μπορούν εύκολα να καταγραφούν σε χαρτί, στη μνήμη του υπολογιστή κ.λπ.

Μαθηματική μοντελοποίηση

Η μαθηματική μοντελοποίηση ανήκει στην κατηγορία της συμβολικής μοντελοποίησης. Επιπλέον, τα μοντέλα μπορούν να δημιουργηθούν από οποιαδήποτε μαθηματικά αντικείμενα: αριθμούς, συναρτήσεις, εξισώσεις κ.λπ.

Κατασκευή μαθηματικού μοντέλου

§ Μπορούν να σημειωθούν διάφορα στάδια κατασκευής ενός μαθηματικού μοντέλου:

1. Κατανοώντας το πρόβλημα, εντοπίζοντας τις πιο σημαντικές ιδιότητες, ιδιότητες, ποσότητες και παραμέτρους για εμάς.

2. Εισαγωγή σημειογραφίας.

3. Κατάρτιση συστήματος περιορισμών που πρέπει να πληρούν οι εισαγόμενες τιμές.

4. Διατύπωση και καταγραφή συνθηκών που πρέπει να ικανοποιούνται από την επιθυμητή βέλτιστη λύση.

Η διαδικασία μοντελοποίησης δεν τελειώνει με τη δημιουργία ενός μοντέλου, αλλά ξεκινά μόνο με αυτό. Έχοντας συντάξει ένα μοντέλο, επιλέγουν μια μέθοδο για να βρουν την απάντηση και λύνουν το πρόβλημα. αφού βρεθεί η απάντηση, συγκρίνεται με την πραγματικότητα. Και είναι πιθανό η απάντηση να μην είναι ικανοποιητική, οπότε το μοντέλο τροποποιείται ή έστω επιλέγεται ένα εντελώς διαφορετικό μοντέλο.

Παράδειγμα μαθηματικού μοντέλου

Εργο

Η ένωση παραγωγής, η οποία περιλαμβάνει δύο εργοστάσια επίπλων, πρέπει να ενημερώσει το μηχανοστάσιο της. Επιπλέον, το πρώτο εργοστάσιο επίπλων πρέπει να αντικαταστήσει τρία μηχανήματα και το δεύτερο - επτά. Οι παραγγελίες μπορούν να γίνουν σε δύο εργοστάσια εργαλειομηχανών. Το πρώτο εργοστάσιο δεν μπορεί να παράγει περισσότερες από 6 μηχανές και το δεύτερο εργοστάσιο θα δεχτεί παραγγελία εάν υπάρχουν τουλάχιστον τρία από αυτά. Πρέπει να καθορίσετε πώς να κάνετε παραγγελίες.

Παράδειγμα 1.5.1.

Αφήστε μια συγκεκριμένη οικονομική περιοχή να παράγει πολλά (ν) είδη προϊόντων αποκλειστικά μόνη της και μόνο για τον πληθυσμό αυτής της περιοχής. Υποτίθεται ότι η τεχνολογική διαδικασία έχει επεξεργαστεί και η ζήτηση του πληθυσμού για αυτά τα αγαθά έχει μελετηθεί. Είναι απαραίτητο να προσδιοριστεί ο ετήσιος όγκος της παραγωγής προϊόντος, λαμβάνοντας υπόψη το γεγονός ότι αυτός ο όγκος πρέπει να παρέχει τόσο την τελική όσο και τη βιομηχανική κατανάλωση.

Ας δημιουργήσουμε ένα μαθηματικό μοντέλο αυτού του προβλήματος. Σύμφωνα με τους όρους του, δίνονται τα ακόλουθα: τύποι προϊόντων, ζήτηση για αυτά και η τεχνολογική διαδικασία. πρέπει να βρείτε τον όγκο παραγωγής κάθε τύπου προϊόντος.

Ας υποδηλώσουμε τις γνωστές ποσότητες:

ντο Εγώ– πληθυσμιακή ζήτηση για Εγώτο προϊόν ( Εγώ=1,...,n); ένα ij- ποσότητα Εγώτο προϊόν που απαιτείται για την παραγωγή μιας μονάδας ιου προϊόντος χρησιμοποιώντας μια δεδομένη τεχνολογία ( Εγώ=1,...,n ; ι=1,...,n);

Χ Εγώ – ένταση εξόδου Εγώ-ο προϊόν ( Εγώ=1,...,n) ολότητα Με =(ντο 1 ,..., ντο n ) ονομάζεται διάνυσμα ζήτησης, αριθμοί ένα ij– τεχνολογικοί συντελεστές και το σύνολο Χ =(Χ 1 ,..., Χ n ) – διάνυσμα απελευθέρωσης.

Σύμφωνα με τις συνθήκες του προβλήματος, το διάνυσμα Χ κατανέμεται σε δύο μέρη: για τελική κατανάλωση (διάνυσμα Με ) και για αναπαραγωγή (διάνυσμα x-s ). Ας υπολογίσουμε αυτό το μέρος του διανύσματος Χ που περνά στην αναπαραγωγή. Σύμφωνα με τις ονομασίες μας για παραγωγή Χ ιποσότητα του jου παρεχόμενου προϊόντος ένα ij · Χ ιποσότητες Εγώ-ο προϊόν.

Μετά το ποσό ένα i1 · Χ 1 +...+ ένα σε · Χ nδείχνει αυτή την αξία Εγώ-ο προϊόν, το οποίο χρειάζεται για όλη την κυκλοφορία Χ =(Χ 1 ,..., Χ n ).

Επομένως, η ισότητα πρέπει να ικανοποιείται:

Επεκτείνοντας αυτό το σκεπτικό σε όλους τους τύπους προϊόντων, φτάνουμε στο επιθυμητό μοντέλο:

Επίλυση αυτού του συστήματος n γραμμικών εξισώσεων για Χ 1 ,...,Χ nκαι βρείτε το απαιτούμενο διάνυσμα απελευθέρωσης.

Για να γράψουμε αυτό το μοντέλο σε πιο συμπαγή (διανυσματική) μορφή, εισάγουμε την ακόλουθη σημείωση:

Τετράγωνο (
) -μήτρα ΕΝΑονομάζεται μήτρα τεχνολογίας. Είναι εύκολο να ελέγξουμε ότι το μοντέλο μας θα γράφεται τώρα ως εξής: x-s=Αχή

(1.6)

Λάβαμε το κλασικό μοντέλο" Εισόδου-εξόδου », συγγραφέας του οποίου είναι ο διάσημος Αμερικανός οικονομολόγος V. Leontiev.

Παράδειγμα 1.5.2.

Το διυλιστήριο πετρελαίου έχει δύο ποιότητες λαδιού: βαθμού ΕΝΑστο ποσό των 10 μονάδων, βαθμός ΣΕ- 15 μονάδες. Κατά τη διύλιση του λαδιού, λαμβάνονται δύο υλικά: βενζίνη (σημαίνουν σι) και μαζούτ ( Μ). Υπάρχουν τρεις επιλογές για τη διαδικασία της τεχνολογίας επεξεργασίας:

Εγώ: 1 μονάδα ΕΝΑ+ 2 μονάδες ΣΕδίνει 3 μονάδες. σι+ 2 μονάδες Μ

II: 2 μονάδες. ΕΝΑ+ 1 μονάδα ΣΕδίνει 1 μονάδα. σι+ 5 μονάδες Μ

III: 2 μονάδες ΕΝΑ+ 2 μονάδες ΣΕδίνει 1 μονάδα. σι+ 2 μονάδες Μ

Η τιμή της βενζίνης είναι $10 ανά μονάδα, το μαζούτ είναι $1 ανά μονάδα.

Είναι απαραίτητο να προσδιοριστεί ο πιο πλεονεκτικός συνδυασμός τεχνολογικών διεργασιών για την επεξεργασία της διαθέσιμης ποσότητας λαδιού.

Πριν από τη μοντελοποίηση, ας διευκρινίσουμε τα ακόλουθα σημεία. Από τις συνθήκες του προβλήματος προκύπτει ότι η «κερδοφορία» της τεχνολογικής διαδικασίας για το εργοστάσιο θα πρέπει να γίνει κατανοητή με την έννοια της απόκτησης μέγιστου εισοδήματος από την πώληση των τελικών προϊόντων του (βενζίνη και μαζούτ). Από αυτή την άποψη, είναι σαφές ότι η «απόφαση επιλογής (λήψης)» του εργοστασίου συνίσταται στον καθορισμό της τεχνολογίας που θα εφαρμοστεί και πόσες φορές. Προφανώς, υπάρχουν πολλές τέτοιες πιθανές επιλογές.

Ας υποδηλώσουμε τις άγνωστες ποσότητες:

Χ Εγώ– ποσότητα χρήσης Εγώη τεχνολογική διαδικασία (i=1,2,3). Άλλες παράμετροι μοντέλου (αποθέματα πετρελαίου, τιμές βενζίνης και μαζούτ) γνωστός.

Τώρα μια συγκεκριμένη φυτική απόφαση καταλήγει στην επιλογή ενός φορέα Χ =(χ 1 ,Χ 2 ,Χ 3 ) , για τα οποία τα έσοδα του εργοστασίου είναι ίσα με (32x 1 +15x 2 +12x 3 ) Εδώ, 32 δολάρια είναι το εισόδημα που λαμβάνεται από μία εφαρμογή της πρώτης τεχνολογικής διαδικασίας ($10 3 μονάδες. σι+ 1 δολάριο · 2 μονάδες. Μ= 32 $). Οι συντελεστές 15 και 12 για τη δεύτερη και τρίτη τεχνολογική διαδικασία, αντίστοιχα, έχουν παρόμοια σημασία. Η λογιστική για τα αποθέματα πετρελαίου οδηγεί στις ακόλουθες συνθήκες:

για ποικιλία ΕΝΑ:

για ποικιλία ΣΕ:,

όπου στους πρώτους συντελεστές ανισότητας 1, 2, 2 είναι τα ποσοστά κατανάλωσης λαδιού βαθμού Α για εφάπαξ χρήση τεχνολογικών διεργασιών Εγώ,II,IIIαντίστοιχα. Οι συντελεστές της δεύτερης ανισότητας έχουν παρόμοια σημασία για λάδι βαθμού Β.

Το μαθηματικό μοντέλο στο σύνολό του έχει τη μορφή:

Βρείτε ένα τέτοιο διάνυσμα x = (x 1 ,Χ 2 ,Χ 3 ) για μεγιστοποίηση

f(x) =32х 1 +15x 2 +12x 3

υπό τις ακόλουθες προϋποθέσεις:

Η συντομευμένη μορφή αυτής της καταχώρησης είναι:

υπό περιορισμούς

(1.7)

Πήραμε το λεγόμενο πρόβλημα γραμμικού προγραμματισμού.

Το μοντέλο (1.7.) είναι ένα παράδειγμα μοντέλου βελτιστοποίησης ντετερμινιστικού τύπου (με καλά καθορισμένα στοιχεία).

Παράδειγμα 1.5.3.

Ένας επενδυτής πρέπει να προσδιορίσει τον καλύτερο συνδυασμό μετοχών, ομολόγων και άλλων τίτλων για αγορά για ένα συγκεκριμένο ποσό, προκειμένου να αποκτήσει ένα συγκεκριμένο κέρδος με ελάχιστο κίνδυνο για τον εαυτό του. Κέρδος ανά δολάριο που επενδύεται σε τίτλο ι- τύπος, που χαρακτηρίζεται από δύο δείκτες: αναμενόμενο κέρδος και πραγματικό κέρδος. Για έναν επενδυτή, είναι επιθυμητό το αναμενόμενο κέρδος ανά δολάριο επένδυσης να μην είναι χαμηλότερο από μια δεδομένη αξία για ολόκληρο το σύνολο των τίτλων σι.

Σημειώστε ότι για τη σωστή μοντελοποίηση αυτού του προβλήματος, ένας μαθηματικός απαιτείται να έχει ορισμένες βασικές γνώσεις στον τομέα της θεωρίας χαρτοφυλακίου κινητών αξιών.

Ας υποδηλώσουμε τις γνωστές παραμέτρους του προβλήματος:

n– αριθμός τύπων τίτλων· ΕΝΑ ι– πραγματικό κέρδος (τυχαίος αριθμός) από τον j-ο τύπο τίτλου. – αναμενόμενο κέρδος από ι-ο τύπος ασφάλειας.

Ας υποδηλώσουμε τις άγνωστες ποσότητες :

y ι - κεφάλαια που διατίθενται για την αγορά τίτλων του τύπου ι.

Χρησιμοποιώντας τη σημείωση μας, ολόκληρο το επενδυμένο ποσό εκφράζεται ως . Για να απλοποιήσουμε το μοντέλο, εισάγουμε νέες ποσότητες

Ετσι, Χ Εγώ- αυτό είναι το μερίδιο όλων των κεφαλαίων που διατίθενται για την απόκτηση τίτλων του είδους ι.

Είναι ξεκάθαρο ότι

Από τις συνθήκες του προβλήματος είναι σαφές ότι ο στόχος του επενδυτή είναι να επιτύχει ένα ορισμένο επίπεδο κέρδους με ελάχιστο κίνδυνο. Ουσιαστικά, ο κίνδυνος είναι ένα μέτρο της απόκλισης του πραγματικού κέρδους από το αναμενόμενο. Επομένως, μπορεί να ταυτιστεί με τη συνδιακύμανση των κερδών για τίτλους τύπου i και τύπου j. Εδώ το M είναι ο προσδιορισμός της μαθηματικής προσδοκίας.

Το μαθηματικό μοντέλο του αρχικού προβλήματος έχει τη μορφή:

υπό περιορισμούς

,
,
,
. (1.8)

Αποκτήσαμε το γνωστό μοντέλο Markowitz για τη βελτιστοποίηση της δομής ενός χαρτοφυλακίου χρεογράφων.

Το μοντέλο (1.8.) είναι ένα παράδειγμα μοντέλου βελτιστοποίησης στοχαστικού τύπου (με στοιχεία τυχαίας).

Παράδειγμα 1.5.4.

Με βάση μια εμπορική οργάνωση, υπάρχουν n τύποι ενός από τα προϊόντα της ελάχιστης ποικιλίας. Μόνο ένας τύπος συγκεκριμένου προϊόντος πρέπει να φέρεται στο κατάστημα. Πρέπει να επιλέξετε τον τύπο του προϊόντος που είναι κατάλληλο να φέρετε στο κατάστημα. Εάν ο τύπος προϊόντος ιθα έχει ζήτηση, το κατάστημα θα έχει κέρδος από την πώλησή του R ι, εάν δεν είναι σε ζήτηση - μια απώλεια q ι .

Πριν από τη μοντελοποίηση, θα συζητήσουμε ορισμένα βασικά σημεία. Σε αυτό το πρόβλημα, ο υπεύθυνος λήψης αποφάσεων (DM) είναι το κατάστημα. Ωστόσο, το αποτέλεσμα (μέγιστο κέρδος) εξαρτάται όχι μόνο από την απόφασή του, αλλά και από το αν το εισαγόμενο προϊόν θα έχει ζήτηση, δηλαδή αν θα αγοραστεί από τον πληθυσμό (υποτίθεται ότι για κάποιο λόγο το κατάστημα δεν έχουν την ευκαιρία να μελετήσουν τη ζήτηση του πληθυσμού ). Επομένως, ο πληθυσμός μπορεί να θεωρηθεί ως δεύτερος λήπτης αποφάσεων, επιλέγοντας το είδος του προϊόντος σύμφωνα με τις προτιμήσεις του. Η χειρότερη «απόφαση» του πληθυσμού για ένα κατάστημα είναι: «τα εισαγόμενα αγαθά δεν έχουν ζήτηση». Έτσι, για να ληφθούν υπόψη όλες οι πιθανές καταστάσεις, το κατάστημα πρέπει να θεωρεί τον πληθυσμό ως «εχθρό» του (υπό όρους), επιδιώκοντας τον αντίθετο στόχο - να ελαχιστοποιήσει το κέρδος του καταστήματος.

Έτσι, έχουμε πρόβλημα λήψης αποφάσεων με δύο συμμετέχοντες που επιδιώκουν αντίθετους στόχους. Ας διευκρινίσουμε ότι το κατάστημα επιλέγει έναν από τους τύπους αγαθών προς πώληση (υπάρχουν n επιλογές απόφασης) και ο πληθυσμός επιλέγει έναν από τους τύπους αγαθών που έχει τη μεγαλύτερη ζήτηση ( nεπιλογές λύσης).

Για να συντάξουμε ένα μαθηματικό μοντέλο, ας σχεδιάσουμε έναν πίνακα με nγραμμές και nστήλες (σύνολο n 2 κελιά) και συμφωνούν ότι οι σειρές αντιστοιχούν στην επιλογή του καταστήματος και οι στήλες στην επιλογή του πληθυσμού. Μετά το κελί (i, j)αντιστοιχεί στην κατάσταση που επιλέγει το κατάστημα Εγώο τύπος προϊόντος ( Εγώ-η γραμμή), και ο πληθυσμός επιλέγει ιο τύπος προϊόντος ( j-η στήλη). Σε κάθε κελί σημειώνουμε μια αριθμητική εκτίμηση (κέρδος ή ζημιά) της αντίστοιχης κατάστασης από την πλευρά του καταστήματος:

Αριθμοί q Εγώγραμμένο με ένα μείον για να αντικατοπτρίζει την απώλεια του καταστήματος. σε κάθε περίπτωση, το «κέρδος» του πληθυσμού (υπό όρους) ισούται με το «κέρδος» του καταστήματος, που λαμβάνεται με το αντίθετο πρόσημο.

Μια συντομευμένη μορφή αυτού του μοντέλου είναι:

(1.9)

Πήραμε το λεγόμενο παιχνίδι matrix. Το μοντέλο (1.9.) είναι ένα παράδειγμα μοντέλων λήψης αποφάσεων παιχνιδιών.