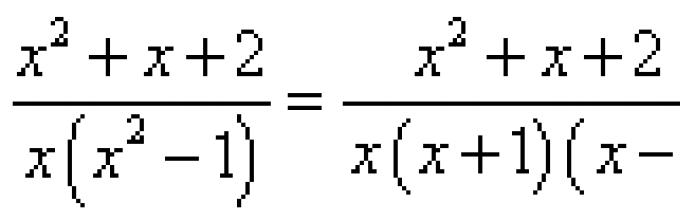Μια ορθολογική συνάρτηση είναι ένα κλάσμα της μορφής, ο αριθμητής και ο παρονομαστής της οποίας είναι πολυώνυμα ή γινόμενα πολυωνύμων.

Παράδειγμα 1. Βήμα 2.

.

Πολλαπλασιάζουμε τους απροσδιόριστους συντελεστές με πολυώνυμα που δεν βρίσκονται σε αυτό το μεμονωμένο κλάσμα, αλλά βρίσκονται σε άλλα κλάσματα που προκύπτουν:

Ανοίγουμε τις αγκύλες και εξισώνουμε τον αριθμητή του αρχικού ολοκληρώματος με την παράσταση που προκύπτει:

Και στις δύο πλευρές της ισότητας, αναζητούμε όρους με τις ίδιες δυνάμεις του x και συνθέτουμε ένα σύστημα εξισώσεων από αυτούς:

.

Ακυρώνουμε όλα τα x και παίρνουμε ένα ισοδύναμο σύστημα εξισώσεων:

.

Έτσι, η τελική επέκταση του ολοκληρώματος σε ένα άθροισμα απλών κλασμάτων είναι:

.

Παράδειγμα 2. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

.

Τώρα αρχίζουμε να ψάχνουμε για αβέβαιους συντελεστές. Για να γίνει αυτό, εξισώνουμε τον αριθμητή του αρχικού κλάσματος στην παράσταση της συνάρτησης με τον αριθμητή της παράστασης που λαμβάνεται μετά την αναγωγή του αθροίσματος των κλασμάτων σε έναν κοινό παρονομαστή:

Τώρα πρέπει να δημιουργήσετε και να λύσετε ένα σύστημα εξισώσεων. Για να γίνει αυτό, εξισώνουμε τους συντελεστές της μεταβλητής στον αντίστοιχο βαθμό στον αριθμητή της αρχικής έκφρασης της συνάρτησης και παρόμοιους συντελεστές στην παράσταση που λήφθηκε στο προηγούμενο βήμα:

Επιλύουμε το σύστημα που προκύπτει:

Λοιπόν, από εδώ

.

Παράδειγμα 3. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

Αρχίζουμε να ψάχνουμε για αβέβαιους συντελεστές. Για να γίνει αυτό, εξισώνουμε τον αριθμητή του αρχικού κλάσματος στην παράσταση της συνάρτησης με τον αριθμητή της παράστασης που λαμβάνεται μετά την αναγωγή του αθροίσματος των κλασμάτων σε έναν κοινό παρονομαστή:

Όπως και στα προηγούμενα παραδείγματα, συνθέτουμε ένα σύστημα εξισώσεων:

Μειώνουμε τα x και παίρνουμε ένα ισοδύναμο σύστημα εξισώσεων:

Λύνοντας το σύστημα, λαμβάνουμε τις ακόλουθες τιμές των αβέβαιων συντελεστών:

Λαμβάνουμε την τελική αποσύνθεση του ολοκληρώματος στο άθροισμα απλών κλασμάτων:

.

Παράδειγμα 4. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

.

Γνωρίζουμε ήδη από προηγούμενα παραδείγματα πώς να εξισώσουμε τον αριθμητή του αρχικού κλάσματος με την έκφραση στον αριθμητή που λαμβάνεται μετά την αποσύνθεση του κλάσματος στο άθροισμα απλών κλασμάτων και τη μεταφορά αυτού του αθροίσματος σε έναν κοινό παρονομαστή. Επομένως, μόνο για λόγους ελέγχου, παρουσιάζουμε το προκύπτον σύστημα εξισώσεων:

Λύνοντας το σύστημα, λαμβάνουμε τις ακόλουθες τιμές των αβέβαιων συντελεστών:

Λαμβάνουμε την τελική αποσύνθεση του ολοκληρώματος στο άθροισμα απλών κλασμάτων:

Παράδειγμα 5. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

.

Μειώνουμε ανεξάρτητα αυτό το άθροισμα σε έναν κοινό παρονομαστή, εξισώνοντας τον αριθμητή αυτής της παράστασης με τον αριθμητή του αρχικού κλάσματος. Το αποτέλεσμα θα πρέπει να είναι το ακόλουθο σύστημα εξισώσεων:

Λύνοντας το σύστημα, λαμβάνουμε τις ακόλουθες τιμές των αβέβαιων συντελεστών:

.

Λαμβάνουμε την τελική αποσύνθεση του ολοκληρώματος στο άθροισμα απλών κλασμάτων:

.

Παράδειγμα 6. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

Εκτελούμε τις ίδιες ενέργειες με αυτό το ποσό όπως στα προηγούμενα παραδείγματα. Το αποτέλεσμα θα πρέπει να είναι το ακόλουθο σύστημα εξισώσεων:

Λύνοντας το σύστημα, λαμβάνουμε τις ακόλουθες τιμές των αβέβαιων συντελεστών:

.

Λαμβάνουμε την τελική αποσύνθεση του ολοκληρώματος στο άθροισμα απλών κλασμάτων:

.

Παράδειγμα 7. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

.

Μετά από ορισμένες ενέργειες με το προκύπτον ποσό, θα πρέπει να ληφθεί το ακόλουθο σύστημα εξισώσεων:

Λύνοντας το σύστημα, λαμβάνουμε τις ακόλουθες τιμές των αβέβαιων συντελεστών:

Λαμβάνουμε την τελική αποσύνθεση του ολοκληρώματος στο άθροισμα απλών κλασμάτων:

.

Παράδειγμα 8. Βήμα 2.Στο βήμα 1, λάβαμε την ακόλουθη αποσύνθεση του αρχικού κλάσματος στο άθροισμα απλών κλασμάτων με απροσδιόριστους συντελεστές στους αριθμητές:

.

Ας κάνουμε μερικές αλλαγές στις ενέργειες που έχουν ήδη τεθεί σε αυτοματοποίηση για να αποκτήσουμε ένα σύστημα εξισώσεων. Υπάρχει μια τεχνητή τεχνική που σε ορισμένες περιπτώσεις βοηθά στην αποφυγή περιττών υπολογισμών. Φέρνοντας το άθροισμα των κλασμάτων σε έναν κοινό παρονομαστή, λαμβάνουμε και εξισώνοντας τον αριθμητή αυτής της παράστασης με τον αριθμητή του αρχικού κλάσματος, παίρνουμε.

Η μέθοδος είναι εφαρμόσιμη για την ελαχιστοποίηση συναρτήσεων λογικής άλγεβρας οποιουδήποτε αριθμού μεταβλητών.

Ας εξετάσουμε την περίπτωση τριών μεταβλητών. Μια Boolean συνάρτηση στο DNF μπορεί να αναπαρασταθεί με τη μορφή όλων των ειδών συνδετικών όρων που μπορούν να συμπεριληφθούν στο DNF:

όπου kО(0,1) είναι συντελεστές. Η μέθοδος συνίσταται στην επιλογή συντελεστών με τέτοιο τρόπο ώστε το DNF που προκύπτει να είναι ελάχιστο.

Αν τώρα ορίσουμε όλες τις πιθανές τιμές των μεταβλητών από το 000 έως το 111, παίρνουμε 2 n (2 3 = 8) εξισώσεις για τον προσδιορισμό των συντελεστών κ:

Λαμβάνοντας υπόψη τα σύνολα για τα οποία η συνάρτηση παίρνει μηδενική τιμή, προσδιορίστε τους συντελεστές που είναι ίσοι με 0 και διαγράψτε τους από τις εξισώσεις των οποίων η δεξιά πλευρά περιέχει 1. Από τους υπόλοιπους συντελεστές σε κάθε εξίσωση, ένας συντελεστής ισοδυναμεί με έναν, που καθορίζει ο σύνδεσμος της κατώτερης βαθμίδας. Οι υπόλοιποι συντελεστές είναι ίσοι με 0. Άρα, οι συντελεστές μονάδας κκαθορίσει την κατάλληλη ελάχιστη μορφή.

Παράδειγμα. Ελαχιστοποιήστε μια δεδομένη συνάρτηση

εάν οι τιμές είναι γνωστές: ; ; ; ; ; ; ; .

Λύση.

Αφού διαγράψουμε τους μηδενικούς συντελεστές παίρνουμε:

=1;

=1;

=1.

Ας εξισώσουμε σε ένα τον συντελεστή που αντιστοιχεί στον σύνδεσμο της χαμηλότερης κατάταξης και μετατρέποντας τις τελευταίες τέσσερις εξισώσεις σε 1, και στην πρώτη εξίσωση είναι σκόπιμο να εξισωθεί ο συντελεστής με 1. Οι υπόλοιποι συντελεστές ορίζονται στο 0.

Απάντηση: τύπος ελαχιστοποιημένης λειτουργίας.

Πρέπει να σημειωθεί ότι η μέθοδος των αόριστων συντελεστών είναι αποτελεσματική όταν ο αριθμός των μεταβλητών είναι μικρός και δεν ξεπερνά τις 5-6.

Πολυδιάστατος κύβος

Ας εξετάσουμε μια γραφική αναπαράσταση μιας συνάρτησης με τη μορφή πολυδιάστατου κύβου. Κάθε κορυφή n-ο διαστατικός κύβος μπορεί να τεθεί σε αντιστοιχία με το συστατικό της μονάδας.

Το υποσύνολο των επισημασμένων κορυφών είναι μια αντιστοίχιση n-διαστατικός κύβος μιας Boolean συνάρτησης από nμεταβλητές στο SDNF.

Για να εμφανίσετε τη λειτουργία από nμεταβλητές που παρουσιάζονται σε οποιοδήποτε DNF, είναι απαραίτητο να δημιουργηθεί μια αντιστοιχία μεταξύ των ελαχίστων και των στοιχείων του n-διαστατικός κύβος.

Μια ελάχιστη κατάταξη (n-1) μπορεί να θεωρηθεί ως το αποτέλεσμα της συγκόλλησης δύο ελαχίστων n-η βαθμίδα, δηλ.

Επί n-διάστατος κύβος που αντιστοιχεί στην αντικατάσταση δύο κορυφών που διαφέρουν μόνο σε τιμές συντεταγμένων x i, συνδέοντας αυτές τις κορυφές με μια ακμή (μια ακμή λέγεται ότι καλύπτει τις κορυφές που προσπίπτουν σε αυτήν).

Έτσι, ελάχιστα ( nΗ -1)η σειρά αντιστοιχεί στις άκρες ενός κύβου ν-διάστασης.

Ομοίως, η αντιστοιχία των ελάχιστων όρων ( n-2)η σειρά πρόσωπα n-διαστατικός κύβος, καθένας από τους οποίους καλύπτει τέσσερις κορυφές (και τέσσερις άκρες).

Στοιχεία n-διαστατικό κύβο, που χαρακτηρίζεται από μικρόονομάζονται μετρήσεις μικρό-κύβους

Άρα οι κορυφές είναι 0-κύβοι, οι ακμές είναι 1-κύβοι, οι όψεις είναι 2-κύβοι κ.λπ.

Συνοψίζοντας, μπορούμε να πούμε ότι η ελάχιστη ( n-S) κατάταξη στο DNF για τη συνάρτηση nμεταβλητές που εμφανίζονται μικρό-ένας κύβος, το καθένα μικρό-ο κύβος καλύπτει όλους εκείνους τους κύβους χαμηλότερης διάστασης που συνδέονται μόνο με τις κορυφές του.

Παράδειγμα. Στο Σχ. δεδομένης της χαρτογράφησης

Εδώ τα ελάχιστα και αντιστοιχούν σε 1-κύβους ( μικρό=3-2=1) και ελάχιστη x 3εμφανίζεται σε 2 κύβους ( μικρό=3-1=2).

Έτσι, οποιοδήποτε DNF αντιστοιχίζεται n-διαστατικός κύβος συνολικά μικρό-κύβους που καλύπτουν όλες τις κορυφές που αντιστοιχούν στις συνιστώσες μονάδες (0-κύβος).

Συστατικά. Για μεταβλητές x 1,x 2,…x nέκφραση ονομάζεται συστατικό της μονάδας, και - συστατικό του μηδέν (σημαίνει είτε είτε).

Αυτό το συστατικό του ενός (μηδέν) μετατρέπεται σε ένα (μηδέν) μόνο με ένα αντίστοιχο σύνολο τιμών μεταβλητών, το οποίο προκύπτει εάν όλες οι μεταβλητές ληφθούν ίσες με ένα (μηδέν) και οι άρνήσεις τους ίσες με μηδέν (ένα).

Για παράδειγμα: το συστατικό ένα αντιστοιχεί στο σύνολο (1011) και το συστατικό μηδέν - σετ (1001).

Δεδομένου ότι το SD(K)NF είναι μια διάσπαση (σύνδεση) των συστατικών του ενός (μηδέν), μπορεί να υποστηριχθεί ότι η συνάρτηση Boole που αντιπροσωπεύει φά(x 1 , x 2 ,…, x n) μετατρέπεται σε ένα (μηδέν) μόνο για σύνολα τιμών μεταβλητών x 1 , x 2 ,…, x n, που αντιστοιχεί σε αυτά τα αναπληρωματικά. Σε άλλα σύνολα αυτή η λειτουργία γίνεται 0 (ένα).

Ισχύει και η αντίθετη δήλωση, στην οποία βασίζεται τρόπο αναπαράστασης οποιουδήποτε Boolean συνάρτηση που καθορίζεται από τον πίνακα.

Για να γίνει αυτό, είναι απαραίτητο να γράψετε διαχωρισμούς (συνδέσεις) των συστατικών του ενός (μηδέν), που αντιστοιχούν σε σύνολα τιμών μεταβλητών στις οποίες η συνάρτηση παίρνει μια τιμή ίση με ένα (μηδέν).

Για παράδειγμα, μια συνάρτηση που δίνεται από έναν πίνακα

ανταποκρίνομαι

Οι εκφράσεις που προκύπτουν μπορούν να μετατραπούν σε άλλη μορφή με βάση τις ιδιότητες της άλγεβρας της λογικής.

Η αντίστροφη πρόταση ισχύει επίσης: αν κάποια συλλογή μικρό-Οι κύβοι καλύπτει το σύνολο όλων των κορυφών που αντιστοιχούν σε μοναδιαίες τιμές της συνάρτησης και στη συνέχεια τον διαχωρισμό που αντιστοιχεί σε αυτές μικρό-Κύβοι ελαχίστων είναι η έκφραση αυτής της συνάρτησης στο DNF.

Λένε ότι μια τέτοια συλλογή μικρό-Οι κύβοι (ή τα αντίστοιχά τους ελάχιστα) σχηματίζουν ένα κάλυμμα της συνάρτησης. Η επιθυμία για μια μινιμαλιστική φόρμα νοείται διαισθητικά ως αναζήτηση μιας τέτοιας κάλυψης, του αριθμού μικρό-από τα οποία θα υπήρχαν λιγότεροι κύβοι, και οι διαστάσεις τους μικρό- περισσότερο. Η κάλυψη που αντιστοιχεί στην ελάχιστη φόρμα ονομάζεται ελάχιστη κάλυψη.

Για παράδειγμα, για τη συνάρτηση στο= η επίστρωση συμμορφώνεται με ένα μη ελάχιστο σχήμα.

Η ισότητα (Ι) είναι ταυτότητα. Αναγωγή του σε ακέραια μορφή, λαμβάνουμε την ισότητα 2 πολυωνύμων. Αλλά αυτή η ισότητα ικανοποιείται πάντα μόνο υπό την προϋπόθεση της ισότητας κάθε όρου αυτών των πολυωνύμων.

Εξισώνοντας τους συντελεστές για τις ίδιες δυνάμεις του x στην αριστερή και τη δεξιά πλευρά της ισότητας, προκύπτει ένα σύστημα γραμμικών εξισώσεων για άγνωστους συντελεστές που πρέπει να λυθούν.

Εφόσον η επέκταση (Ι) υπάρχει πάντα για οποιοδήποτε σωστό ορθολογικό κλάσμα, το σύστημα που προκύπτει είναι πάντα συνεπές.

Αυτή η μέθοδος εύρεσης συντελεστών ονομάζεται μέθοδος αβέβαιων συντελεστών (μέθοδος σύγκρισης συντελεστών).

Ας δώσουμε ένα παράδειγμα αποσύνθεσης μιας λογικής συνάρτησης σε στοιχειώδη κλάσματα.

Παράδειγμα 6.6.27. Χωρίστε τα κλάσματα σε στοιχειώδη κλάσματα.

αντικαταστήστε την τελευταία εξίσωση με τη δεύτερη

Ετσι,
.

x=2 ;

x=3 .

Πρέπει; .

Η μέθοδος μερικής αξίας απαιτεί λιγότερη εργασία και επομένως αξίζει ιδιαίτερη προσοχή κατά την ολοκλήρωση ορθολογικών κλασμάτων.

Εάν οι ρίζες του παρονομαστή είναι μόνο πραγματικές, τότε είναι σκόπιμο να χρησιμοποιήσετε αυτήν τη μέθοδο για να καθορίσετε άγνωστους συντελεστές.

Σε άλλες περιπτώσεις, και οι δύο μέθοδοι μπορούν να συνδυαστούν για τον προσδιορισμό άγνωστων συντελεστών.

Σχόλιο. Η μέθοδος των μερικών τιμών χρησιμοποιείται επίσης σε άλλες περιπτώσεις, αλλά εδώ πρέπει να διαφοροποιηθεί η ταυτότητα.

Έτσι, για να ενσωματωθούν σωστά ρητά κλάσματα αρκεί να μπορούμε:

1) ενσωμάτωση στοιχειωδών κλασμάτων.

2) να αποσυνθέσετε τα ορθολογικά κλάσματα σε στοιχειώδη.

3. Ολοκλήρωση ορθολογικών κλασμάτων

Σχέδιο για την ολοκλήρωση ορθολογικών κλασμάτων:

Για να ενσωματώσετε ρητά κλάσματα ;

Όπου τα P(x) και Q(x) είναι πολυώνυμα με πραγματικούς συντελεστές, εκτελούνται τρία βήματα διαδοχικά.

Το πρώτο βήμα. Εάν το κλάσμα είναι ακατάλληλο, δηλαδή ο βαθμός του αριθμητή P(x) είναι μεγαλύτερος ή ίσος με τον βαθμό του παρονομαστή Q(x), απομονώστε ολόκληρο το τμήμα του ορθολογικού κλάσματος διαιρώντας τον αριθμητή με τον παρονομαστή σύμφωνα με στον κανόνα για τη διαίρεση ενός πολυωνύμου με ένα πολυώνυμο. Μετά από αυτό, το ορθολογικό κλάσμα μπορεί να γραφτεί ως άθροισμα:

1) το επιλεγμένο ακέραιο μέρος – το πολυώνυμο M(x);

2) σωστό υπολειπόμενο κλάσμα :

Δεύτερο βήμα.

Σωστό υπόλοιπο κλάσμα αποσυντίθεται σε επόμενα κλάσματα.

Για να το κάνετε αυτό, βρείτε τις ρίζες της εξίσωσης Q(x)=0 και αποσυνθέστε τον παρονομαστή Q(x) σε συντελεστές του πρώτου και δεύτερου βαθμού με πραγματικούς συντελεστές:

Σε αυτή την επέκταση του παρονομαστή, οι συντελεστές του 1ου βαθμού αντιστοιχούν σε πραγματικές ρίζες και οι συντελεστές του 2ου βαθμού αντιστοιχούν σε παράλληλες συζυγείς ρίζες.

Ο συντελεστής για μεγαλύτερο βαθμό x στον παρονομαστή Q(x) μπορεί να θεωρηθεί ίσος με 1, αφού αυτό μπορεί πάντα να επιτευχθεί διαιρώντας τα P(x) και Q(x) με αυτόν.

Μετά από αυτό, το κατάλληλο υπολειπόμενο κλάσμα αποσυντίθεται σε απλούστερα (στοιχειώδη) κλάσματα.

Τρίτο βήμα. Βρείτε τα ολοκληρώματα του επιλεγμένου ακέραιου μέρους και όλα τα στοιχειώδη κλάσματα (χρησιμοποιώντας τις μεθόδους που αναφέρθηκαν παραπάνω), τα οποία στη συνέχεια προστίθενται.

Παράδειγμα 6.6.28.

Κάτω από το ολοκλήρωμα υπάρχει ένα ακατάλληλο ορθολογικό κλάσμα, αφού ο βαθμός του αριθμητή είναι ίσος με τον βαθμό του παρονομαστή, οπότε επιλέγουμε το ακέραιο μέρος.

ΥΠΟΥΡΓΕΙΟ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΠΑΙΔΕΙΑΣ ΤΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΟΥ BASHKORTO STAN

SAOU SPO Bashkir College of Architecture and Civil Engineering

Khaliullin Askhat Adelzyanovich,

καθηγητής μαθηματικών στο Bashkirsky

Κολλέγιο Αρχιτεκτόνων και Πολιτικών Μηχανικών

UFA

2014

Εισαγωγή _________________________________________________3

Κεφάλαιο ΕΓΩ. Θεωρητικές όψεις της χρήσης της μεθόδου των αβέβαιων συντελεστών________________________________________________4

Κεφάλαιο II. Αναζητά λύσεις σε προβλήματα με πολυώνυμα χρησιμοποιώντας τη μέθοδο των αόριστων συντελεστών_________________________________7

2.1. Παραγοντοποίηση πολυωνύμου_____________________ 7

2.2. Προβλήματα με παραμέτρους________________________________ 10

2.3. Επίλυση εξισώσεων________________________________________________14

2.4. Λειτουργικές εξισώσεις________________________________19

Συμπέρασμα________________________________________________23

Κατάλογος χρησιμοποιημένης βιβλιογραφίας________________________________________________24

Εφαρμογή ________________________________________________25

Εισαγωγή.

Αυτή η εργασία είναι αφιερωμένη στις θεωρητικές και πρακτικές πτυχές της εισαγωγής της μεθόδου των αόριστων συντελεστών στο σχολικό μάθημα των μαθηματικών. Η συνάφεια αυτού του θέματος καθορίζεται από τις ακόλουθες συνθήκες.

Κανείς δεν θα υποστηρίξει ότι τα μαθηματικά ως επιστήμη δεν στέκονται σε ένα μέρος, εξελίσσονται συνεχώς, εμφανίζονται νέα καθήκοντα αυξημένης πολυπλοκότητας, τα οποία συχνά προκαλούν ορισμένες δυσκολίες, καθώς αυτές οι εργασίες συνήθως συνδέονται με την έρευνα. Τα τελευταία χρόνια, τέτοια προβλήματα έχουν προταθεί σε σχολικές, επαρχιακές και δημοκρατικές μαθηματικές Ολυμπιάδες, και είναι επίσης διαθέσιμα στις εκδόσεις του Unified State Exam. Ως εκ τούτου, απαιτήθηκε μια ειδική μέθοδος που θα επέτρεπε σε τουλάχιστον ορισμένες από αυτές να επιλυθούν πιο γρήγορα, αποτελεσματικά και οικονομικά. Αυτή η εργασία παρουσιάζει ξεκάθαρα το περιεχόμενο της μεθόδου των αόριστων συντελεστών, η οποία χρησιμοποιείται ευρέως σε μια μεγάλη ποικιλία τομέων των μαθηματικών, που κυμαίνονται από ερωτήσεις που περιλαμβάνονται στο μάθημα γενικής εκπαίδευσης έως τα πιο προχωρημένα μέρη του. Ειδικότερα, οι εφαρμογές της μεθόδου των αόριστων συντελεστών στην επίλυση προβλημάτων με παραμέτρους, κλασματικές ορθολογικές και συναρτησιακές εξισώσεις είναι ιδιαίτερα ενδιαφέρουσες και αποτελεσματικές. μπορούν εύκολα να ενδιαφέρουν όποιον ενδιαφέρεται για τα μαθηματικά. Ο κύριος σκοπός της προτεινόμενης εργασίας και της επιλογής προβλημάτων είναι η παροχή άφθονων ευκαιριών για τη βελτίωση και την ανάπτυξη της ικανότητας εύρεσης σύντομων και μη τυπικών λύσεων.

Η εργασία αυτή αποτελείται από δύο κεφάλαια. Το πρώτο συζητά τις θεωρητικές πτυχές της χρήσης

μέθοδος αβέβαιων συντελεστών, και δεύτερον, πρακτικές και μεθοδολογικές πτυχές αυτής της χρήσης.

Το παράρτημα της εργασίας παρέχει προϋποθέσεις για συγκεκριμένες εργασίες για ανεξάρτητη λύση.

Κεφάλαιο Εγώ . Θεωρητικές πτυχές χρήσηςμέθοδος αβέβαιων συντελεστών

«Ο άνθρωπος... γεννήθηκε για να γίνει κύριος,

κυβερνήτης, βασιλιάς της φύσης, αλλά σοφία,

με το οποίο πρέπει να κυβερνήσει δεν του δίνεται

από τη γέννηση: αποκτάται με τη μάθηση»

N.I.Lobachevsky

Υπάρχουν διάφοροι τρόποι και μέθοδοι επίλυσης προβλημάτων, αλλά ένας από τους πιο βολικούς, πιο αποτελεσματικούς, πρωτότυπους, κομψούς και ταυτόχρονα πολύ απλούς και κατανοητούς σε όλους είναι η μέθοδος των αόριστων συντελεστών. Η μέθοδος των απροσδιόριστων συντελεστών είναι μια μέθοδος που χρησιμοποιείται στα μαθηματικά για την εύρεση των συντελεστών των παραστάσεων των οποίων η μορφή είναι γνωστή εκ των προτέρων.

Πριν εξετάσουμε την εφαρμογή της μεθόδου των αόριστων συντελεστών στην επίλυση διαφόρων τύπων προβλημάτων, παρουσιάζουμε μια σειρά θεωρητικών πληροφοριών.

Ας δοθούν

ΕΝΑ n (Χ) = ένα 0 Χ n + ένα 1 Χ n-1 + ένα 2 Χ n-2 + ··· + ένα n-1 Χ + ένα n

σι Μ (Χ ) = σι 0 Χ Μ + σι 1 Χ Μ -1 + σι 2 Χ Μ -2 + ··· + σι m-1 Χ + σι Μ ,

πολυώνυμα σχετικά Χμε οποιεσδήποτε πιθανότητες.

Θεώρημα. Δύο πολυώνυμα ανάλογα με το ένα και το ίδιο όρισμα είναι πανομοιότυπα ίσα αν και μόνο ανn = Μ και οι αντίστοιχοι συντελεστές τους είναι ίσοιένα 0 = σι 0 , ένα 1 = σι 1 , ένα 2 = σι 2 ,··· , ένα n -1 = σι Μ -1 , ένα n = σι Μ Και Τ. ρε.

Προφανώς, ίσα πολυώνυμα παίρνουν όλες τις τιμές Χίδιες αξίες. Αντίθετα, αν οι τιμές δύο πολυωνύμων είναι ίσες για όλες τις τιμές Χ, μετά τα πολυώνυμα είναι ίσοι, δηλαδή οι συντελεστές τους στους ίδιους βαθμούςΧταιριάξει.

Επομένως, η ιδέα της εφαρμογής της μεθόδου των αόριστων συντελεστών για την επίλυση προβλημάτων είναι η εξής.

Ας γνωρίζουμε ότι ως αποτέλεσμα ορισμένων μετασχηματισμών προκύπτει μια έκφραση ενός συγκεκριμένου τύπου και μόνο οι συντελεστές σε αυτήν την παράσταση είναι άγνωστοι. Τότε αυτοί οι συντελεστές χαρακτηρίζονται με γράμματα και θεωρούνται άγνωστοι. Στη συνέχεια κατασκευάζεται ένα σύστημα εξισώσεων για τον προσδιορισμό αυτών των αγνώστων.

Για παράδειγμα, στην περίπτωση πολυωνύμων, αυτές οι εξισώσεις γίνονται από την προϋπόθεση ότι οι συντελεστές είναι ίσοι για τις ίδιες δυνάμεις Χγια δύο ίσα πολυώνυμα.

Θα δείξουμε αυτό που ειπώθηκε παραπάνω χρησιμοποιώντας τα ακόλουθα συγκεκριμένα παραδείγματα και ας ξεκινήσουμε με το πιο απλό.

Έτσι, για παράδειγμα, με βάση θεωρητικές εκτιμήσεις, το κλάσμα

μπορεί να αναπαρασταθεί ως άθροισμα

, Οπου ένα , σι Και ντο - συντελεστές που θα καθοριστούν. Για να τα βρούμε, εξισώνουμε τη δεύτερη έκφραση με την πρώτη:

=

και απελευθερώνοντας τον εαυτό μας από τον παρονομαστή και συλλέγοντας όρους με τις ίδιες δυνάμεις στα αριστερά Χ, παίρνουμε:

(ένα + σι + ντο )Χ 2 + ( σι - ντο )x - a = 2Χ 2 – 5 Χ– 1

Αφού η τελευταία ισότητα πρέπει να ισχύει για όλες τις αξίες Χ, τότε οι συντελεστές στους ίδιους βαθμούςΧδεξιά και αριστερά πρέπει να είναι ίδια. Έτσι, λαμβάνονται τρεις εξισώσεις για τον προσδιορισμό των τριών άγνωστων συντελεστών:

α+β+γ = 2

σι - ντο = - 5

ΕΝΑ= 1, από όπου ένα = 1 , σι = - 2 , ντο = 3

Ως εκ τούτου,

=
,

η εγκυρότητα αυτής της ισότητας είναι εύκολο να επαληθευτεί άμεσα.

Ας υποθέσουμε ότι πρέπει επίσης να αναπαραστήσετε ένα κλάσμα

όπως και ένα + σι
+ ντο
+ ρε
, Οπου ένα , σι , ντο Και ρε- άγνωστοι ορθολογικοί συντελεστές. Εξισώνουμε τη δεύτερη έκφραση με την πρώτη:

ένα + σι
+ ντο
+ ρε
=
ή, Απελευθερώνοντας τον εαυτό μας από τον παρονομαστή, αφαιρώντας, όπου είναι δυνατόν, λογικούς παράγοντες κάτω από τα σημάδια των ριζών και φέρνοντας παρόμοιους όρους στην αριστερή πλευρά, λαμβάνουμε:

(ένα- 2 σι + 3 ντο ) + (- α+β +3 ρε )
+ (α+γ - 2 ρε )
+

+ (προ ΧΡΙΣΤΟΥ + ρε )
= 1 +
-
.

Αλλά μια τέτοια ισότητα είναι δυνατή μόνο στην περίπτωση που οι ορθολογικοί όροι και των δύο μερών και οι συντελεστές των ίδιων ριζών είναι ίσοι. Έτσι, προκύπτουν τέσσερις εξισώσεις για την εύρεση των άγνωστων συντελεστών ένα , σι , ντο Και ρε :

ένα- 2β+ 3ντο = 1

- α+β +3 ρε = 1

α+γ - 2 ρε = - 1

σι - ντο + ρε= 0, εξ ου και ένα = 0 ; σι = - ; ντο = 0 ; ρε= , δηλαδή
= -
+
.

Κεφάλαιο II. Αναζητά λύσεις σε προβλήματα με πολυώνυμα μέθοδος απροσδιόριστων συντελεστών.

«Τίποτα δεν συμβάλλει στην κατάκτηση ενός θέματος καλύτερα από

τον τρόπο να ενεργείς μαζί του σε διαφορετικές καταστάσεις»

Ακαδημαϊκός B.V. Gnedenko

2. 1. Παραγοντοποίηση πολυωνύμου.

Μέθοδοι παραγοντοποίησης πολυωνύμων:

1) τοποθέτηση του κοινού παράγοντα εκτός παρενθέσεων, 2) μέθοδος ομαδοποίησης. 3) εφαρμογή βασικών τύπων πολλαπλασιασμού. 4) εισαγωγή βοηθητικών όρων 5) προκαταρκτικός μετασχηματισμός ενός δεδομένου πολυωνύμου χρησιμοποιώντας ορισμένους τύπους. 6) επέκταση με την εύρεση των ριζών ενός δεδομένου πολυωνύμου. 7) μέθοδος εισαγωγής της παραμέτρου. 8)μέθοδος απροσδιόριστων συντελεστών.

Πρόβλημα 1. Παράγοντας το πολυώνυμο σε πραγματικούς συντελεστές Χ 4 + Χ 2 + 1 .

Λύση. Δεν υπάρχουν ρίζες μεταξύ των διαιρετών του ελεύθερου όρου αυτού του πολυωνύμου. Δεν μπορούμε να βρούμε τις ρίζες του πολυωνύμου με άλλα στοιχειώδη μέσα. Επομένως, δεν είναι δυνατό να πραγματοποιηθεί η απαιτούμενη επέκταση βρίσκοντας πρώτα τις ρίζες αυτού του πολυωνύμου. Μένει να αναζητήσουμε λύση στο πρόβλημα είτε με την εισαγωγή βοηθητικών όρων είτε με τη μέθοδο των απροσδιόριστων συντελεστών. Είναι προφανές ότι Χ 4 + Χ 2 + 1 = Χ 4 + Χ 3 + Χ 2 - Χ 3 - Χ 2 - Χ + Χ 2 + Χ + 1 =

= Χ 2 (Χ 2 + Χ + 1) - Χ (Χ 2 + Χ + 1) + Χ 2 + Χ + 1 =

= (Χ 2 + Χ + 1)(Χ 2 - Χ + 1).

Τα προκύπτοντα τετραγωνικά τριώνυμα δεν έχουν ρίζες και επομένως είναι αδιάσπαστα σε πραγματικούς γραμμικούς παράγοντες.

Η περιγραφόμενη μέθοδος είναι τεχνικά απλή, αλλά δύσκολη λόγω της τεχνητότητάς της. Πράγματι, είναι πολύ δύσκολο να καταλήξουμε στους απαιτούμενους βοηθητικούς όρους. Μόνο μια εικασία μας βοήθησε να βρούμε αυτήν την αποσύνθεση. Αλλά

Υπάρχουν πιο αξιόπιστοι τρόποι επίλυσης τέτοιων προβλημάτων.

Θα μπορούσε κανείς να προχωρήσει ως εξής: να υποθέσουμε ότι το δεδομένο πολυώνυμο αποσυντίθεται στο γινόμενο

(Χ 2 + ΕΝΑ Χ + σι )(Χ 2 + ντο Χ + ρε )

δύο τετράγωνα τριώνυμα με ακέραιους συντελεστές.

Έτσι, θα το έχουμε

Χ 4 + Χ 2 + 1 = (Χ 2 + ΕΝΑ Χ + σι )(Χ 2 + ντο Χ + ρε )

Μένει να καθοριστούν οι συντελεστέςένα , σι , ντο Και ρε .

Πολλαπλασιάζοντας τα πολυώνυμα στη δεξιά πλευρά της τελευταίας ισότητας, παίρνουμε:Χ 4 + Χ 2 + 1 = Χ 4 +

+ (α + γ ) Χ 3 + (σι + ΕΝΑ ντο + ρε ) Χ 2 + (Ενα δ + προ ΧΡΙΣΤΟΥ ) x + βδ .

Αλλά επειδή χρειαζόμαστε τη δεξιά πλευρά αυτής της ισότητας να μετατραπεί στο ίδιο πολυώνυμο που βρίσκεται στην αριστερή πλευρά, θα απαιτήσουμε να πληρούνται οι ακόλουθες προϋποθέσεις:

α + γ = 0

σι + ΕΝΑ ντο + ρε = 1

Ενα δ + προ ΧΡΙΣΤΟΥ = 0

βδ = 1 .

Το αποτέλεσμα είναι ένα σύστημα τεσσάρων εξισώσεων με τέσσερις αγνώστουςένα , σι , ντο Και ρε . Είναι εύκολο να βρείτε τους συντελεστές από αυτό το σύστημαένα = 1 , σι = 1 , ντο = -1 Και ρε = 1.

Τώρα το πρόβλημα έχει λυθεί πλήρως. Πήραμε:

Χ 4 + Χ 2 + 1 = (Χ 2 + Χ + 1)(Χ 2 - Χ + 1).

Πρόβλημα 2. Παράγοντας το πολυώνυμο σε πραγματικούς συντελεστές Χ 3 – 6 Χ 2 + 14 Χ – 15 .

Λύση. Ας αναπαραστήσουμε αυτό το πολυώνυμο στη μορφή

Χ 3 – 6 Χ 2 + 14 Χ – 15 = (Χ + ΕΝΑ )(Χ 2 + bx + ντο) , Οπου ένα , σι Και Με - συντελεστές που δεν έχουν ακόμη καθοριστεί. Αφού δύο πολυώνυμα είναι πανομοιότυπα ίσα αν και μόνο αν οι συντελεστές των ίδιων δυνάμεωνΧ είναι ίσα, λοιπόν, εξισώνοντας τους συντελεστές αντίστοιχα γιαΧ 2 , Χ και ελεύθεροι όροι, λαμβάνουμε ένα σύστημα τριών εξισώσεων με τρεις αγνώστους:

α+β= - 6

αβ + γ = 14

μετα Χριστον = - 15 .

Η λύση σε αυτό το σύστημα θα απλοποιηθεί σημαντικά αν λάβουμε υπόψη ότι ο αριθμός 3 (διαιρέτης του ελεύθερου όρου) είναι η ρίζα αυτής της εξίσωσης και, επομένως,ένα = - 3 ,

σι = - 3 Και Με = 5 .

Επειτα Χ 3 – 6 Χ 2 + 14 Χ – 15 = (Χ – 3)(Χ 2 – 3 Χ + 5).

Η εφαρμοσμένη μέθοδος των αόριστων συντελεστών, σε σύγκριση με την παραπάνω μέθοδο εισαγωγής βοηθητικών όρων, δεν περιέχει τίποτα τεχνητό, αλλά απαιτεί την εφαρμογή πολλών θεωρητικών αρχών και συνοδεύεται από αρκετά μεγάλους υπολογισμούς. Για πολυώνυμα υψηλότερου βαθμού, αυτή η μέθοδος απροσδιόριστων συντελεστών οδηγεί σε δυσκίνητα συστήματα εξισώσεων.

2.2.Εργασίες και με παραμέτρους.

Τα τελευταία χρόνια, οι εκδόσεις του Unified State Exam προσφέρουν εργασίες με παραμέτρους. Η επίλυσή τους συχνά προκαλεί ορισμένες δυσκολίες. Κατά την επίλυση προβλημάτων με παραμέτρους, μαζί με άλλες μεθόδους, μπορείτε να χρησιμοποιήσετε αρκετά αποτελεσματικά τη μέθοδο των αόριστων συντελεστών. Είναι αυτή η μέθοδος που σας επιτρέπει να απλοποιήσετε σημαντικά τη λύση τους και να λάβετε γρήγορα μια απάντηση.

Εργασία 3. Προσδιορίστε σε ποιες τιμές της παραμέτρου ΕΝΑεξίσωση 2 Χ 3 – 3 Χ 2 – 36 Χ + ΕΝΑ – 3 = 0 έχει ακριβώς δύο ρίζες.

Λύση. 1 τρόπος. Χρησιμοποιώντας παράγωγο.

Ας αναπαραστήσουμε αυτή την εξίσωση με τη μορφή δύο συναρτήσεων

2 x 3 – 3 Χ 2 – 36 Χ – 3 = – ΕΝΑ .

φά (Χ) = 2x 3 – 3 Χ 2 – 36 Χ– 3 και φ( Χ ) = – ΕΝΑ .

Ας εξερευνήσουμε τη λειτουργίαφά (Χ) = 2x 3 – 3 Χ 2 – 36 Χ – 3 χρησιμοποιώντας την παράγωγο και να κατασκευάσετε σχηματικά τη γραφική παράσταση της (Εικ. 1.).

φά( – Χ )φά (Χ ) , φά (– Χ ) – φά (Χ ). Η συνάρτηση δεν είναι ούτε άρτια ούτε περιττή.

3. Ας βρούμε τα κρίσιμα σημεία της συνάρτησης, τα διαστήματα αύξησης και μείωσης της, ακρότατα. φά / (Χ ) = 6 Χ 2 – 6 Χ – 36. ρε (φά / ) = R , επομένως θα βρούμε όλα τα κρίσιμα σημεία της συνάρτησης λύνοντας την εξίσωση φά / (Χ ) = 0 .

6(Χ 2 – Χ– 6) = 0 ,

Χ 2 – Χ– 6 = 0 ,

Χ 1 = 3 , Χ 2 = – 2 από το θεώρημα αντίστροφο προς το θεώρημα του Vieta.

φά / (Χ ) = 6(Χ – 3)(Χ + 2).

+ Μέγιστη - ελάχ +

2 3 Χ

φά / (Χ) > 0 για όλα Χ< – 2 και Χ > 3 και η συνάρτηση είναι συνεχής σε σημείαx =– 2 και Χ = 3, επομένως, αυξάνεται σε κάθε ένα από τα διαστήματα (- ; - 2] και [ 3 ; ).

φά / (Χ ) < 0 σε - 2 < Χ< 3, επομένως, μειώνεται στο διάστημα [- 2; 3 ].

Χ = - 2ος μέγιστος βαθμός, επειδή σε αυτό το σημείο το πρόσημο της παραγώγου αλλάζει από"+" σε "-".

φά (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,

x = 3 ελάχιστος βαθμός, αφού σε αυτό το σημείο αλλάζει το πρόσημο της παραγώγου"-" σε "+".

φά (3) = 2·27 – 3,9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.

Γράφημα της συνάρτησης φ(Χ ) = – ΕΝΑ είναι μια ευθεία παράλληλη προς τον άξονα x και που διέρχεται από το σημείο με συντεταγμένες (0; – ΕΝΑ ). Τα γραφήματα έχουν δύο κοινά σημεία:ΕΝΑ= 41, δηλ. α =– 41 και – ΕΝΑ= – 84, δηλ. ΕΝΑ = 84 .

στο

41φ( Χ)

2 3 Χ

3 φά ( Χ ) = 2 x 3 – 3 Χ 2 – 36 Χ – 3

Μέθοδος 2. Μέθοδος απροσδιόριστων συντελεστών.

Εφόσον, σύμφωνα με τις συνθήκες του προβλήματος, αυτή η εξίσωση πρέπει να έχει μόνο δύο ρίζες, η ισότητα είναι προφανής:

2Χ 3 – 3 Χ 2 – 36 Χ + ΕΝΑ – 3 = (x + σι ) 2 (2 Χ + ντο ) ,

2Χ 3 – 3 Χ 2 – 36 Χ + ΕΝΑ – 3 = 2 Χ 3 + (4 σι + ντο ) Χ 2 + (2 σι 2 + +2 προ ΧΡΙΣΤΟΥ ) Χ + σι 2 ντο ,

Τώρα εξισώνοντας τους συντελεστές στις ίδιες μοίρες Χ, παίρνουμε ένα σύστημα εξισώσεων

4 β + γ = - 3

2σι 2 + 2π.Χ. = - 36

σι 2 ντο = ένα – 3 .

Από τις δύο πρώτες εξισώσεις του συστήματος βρίσκουμεσι 2 + σι – 6 = 0, εξ ου και σι 1 = - 3 ή σι 2 = 2. Αντίστοιχες τιμέςΜε 1 και Με 2 εύκολο να βρεθεί από την πρώτη εξίσωση του συστήματος:Με 1 = 9 ή Με 2 = - 11 . Τέλος, η επιθυμητή τιμή της παραμέτρου μπορεί να προσδιοριστεί από την τελευταία εξίσωση του συστήματος:

ΕΝΑ = σι 2 ντο + 3 , ένα 1 = - 41 ή ένα 2 = 84.

Απάντηση: αυτή η εξίσωση έχει ακριβώς δύο διαφορετικές

ρίζα σε ΕΝΑ= - 41 και ΕΝΑ= 84 .

Εργασία 4. Βρείτε τη μεγαλύτερη τιμή της παραμέτρουΕΝΑ , για το οποίο η εξίσωσηΧ 3 + 5 Χ 2 + Ω + σι = 0

με ακέραιους συντελεστές έχει τρεις διαφορετικές ρίζες, η μία από τις οποίες είναι ίση με – 2.

Λύση. 1 τρόπος. Αντικατάσταση Χ= - 2 στην αριστερή πλευρά της εξίσωσης, παίρνουμε

8 + 20 – 2 ΕΝΑ + σι= 0, που σημαίνει σι = 2 ένα – 12 .

Δεδομένου ότι ο αριθμός - 2 είναι ρίζα, μπορούμε να βγάλουμε τον κοινό παράγοντα Χ + 2:

Χ 3 + 5 Χ 2 + Ω + σι = Χ 3 + 2 Χ 2 + 3 Χ 2 + Ω + (2 ένα – 12) =

= Χ 2 (Χ + 2) + 3 Χ (Χ + 2) – 6 Χ + Ω + (2 ένα – 12) =

= Χ 2 (Χ + 2) + 3 Χ (Χ + 2) + (ένα – 6)(Χ +2) - 2(ένα – 6)+ (2 ένα - 12) =

= (Χ + 2)(Χ 2 + 3 Χ + (ένα – 6) ) .

Κατά συνθήκη, υπάρχουν δύο ακόμη ρίζες της εξίσωσης. Αυτό σημαίνει ότι η διάκριση του δεύτερου παράγοντα είναι θετική.

ρε =3 2 - 4 (ένα – 6) = 33 – 4 ένα > 0, δηλαδή ΕΝΑ < 8,25 .

Φαίνεται ότι η απάντηση θα ήταν α = 8 . Αλλά όταν αντικαταστήσουμε τον αριθμό 8 στην αρχική εξίσωση παίρνουμε:

Χ 3 + 5 Χ 2 + Ω + σι = Χ 3 + 5 Χ 2 + 8 Χ + 4 = (Χ + 2)(Χ 2 + 3 Χ + 2 ) =

= (Χ + 1) (Χ + 2) 2 ,

δηλαδή η εξίσωση έχει μόνο δύο διαφορετικές ρίζες. Αλλά όταν α =Το 7 παράγει στην πραγματικότητα τρεις διαφορετικές ρίζες.

Μέθοδος 2. Μέθοδος απροσδιόριστων συντελεστών.

Αν η εξίσωση Χ 3 + 5 Χ 2 + Ω + σι = 0 έχει ρίζα Χ = - 2, τότε μπορείτε πάντα να σηκώνετε τους αριθμούςντο Και ρε ώστε μπροστά σε όλουςΧ η ισότητα ήταν αληθινή

Χ 3 + 5 Χ 2 + Ω + σι = (Χ + 2)(Χ 2 + Με Χ + ρε ).

Για να βρείτε αριθμούςντο Και ρε Ας ανοίξουμε τις αγκύλες στη δεξιά πλευρά, ας προσθέσουμε παρόμοιους όρους και πάρουμε

Χ 3 + 5 Χ 2 + Ω + σι = Χ 3 + (2 + Με ) Χ 2 +(2 s + ρε ) Χ + 2 ρε

Εξίσωση των συντελεστών στις αντίστοιχες δυνάμεις Χέχουμε σύστημα

2 + Με = 5

2 Με + ρε = ένα

2 ρε = σι , που γ = 3 .

Ως εκ τούτου, Χ 2 + 3 Χ + ρε = 0 , ρε = 9 – 4 ρε > 0 ή

ρε < 2.25, άρα ρε (- ; 2 ].

Οι συνθήκες του προβλήματος ικανοποιούνται από την τιμή ρε = 1 . Η τελική επιθυμητή τιμή της παραμέτρουΕΝΑ = 7.

ΑΠΑΝΤΗΣΗ: πότε α = 7 αυτή η εξίσωση έχει τρεις διαφορετικές ρίζες.

2.3. Επίλυση εξισώσεων.

«Να θυμάστε ότι λύνοντας μικρά προβλήματα σας

προετοιμαστείτε για να αντιμετωπίσετε μεγάλα και δύσκολα

νέα καθήκοντα».

Ακαδημαϊκός S.L. Sobolev

Όταν λύνετε κάποιες εξισώσεις, μπορείτε και πρέπει να δείξετε επινοητικότητα και εξυπνάδα και να χρησιμοποιήσετε ειδικές τεχνικές. Η γνώση μιας ποικιλίας τεχνικών μετασχηματισμού και η ικανότητα εκτέλεσης λογικού συλλογισμού έχει μεγάλη σημασία στα μαθηματικά. Ένα από αυτά τα κόλπα είναι να προσθέσετε και να αφαιρέσετε κάποια καλά επιλεγμένη έκφραση ή αριθμό. Το ίδιο το δηλωμένο γεγονός, φυσικά, είναι γνωστό σε όλους - η κύρια δυσκολία είναι να δούμε σε μια συγκεκριμένη διαμόρφωση εκείνους τους μετασχηματισμούς των εξισώσεων στις οποίες είναι βολικό και σκόπιμο να το εφαρμόσουμε.

Χρησιμοποιώντας μια απλή αλγεβρική εξίσωση, θα παρουσιάσουμε μια μη τυπική τεχνική για την επίλυση εξισώσεων.

Πρόβλημα 5. Λύστε την εξίσωση

=
.

Λύση. Ας πολλαπλασιάσουμε και τις δύο πλευρές αυτής της εξίσωσης επί 5 και ας την ξαναγράψουμε ως εξής

= 0 ; Χ 0; -
;

= 0 ,

= 0 ,

= 0 ή
= 0

Ας λύσουμε τις εξισώσεις που προκύπτουν χρησιμοποιώντας τη μέθοδο των απροσδιόριστων συντελεστών

Χ 4 - Χ 3 –7 Χ – 3 = (Χ 2 + αχ + σι )(Χ 2 + cx + ρε ) = 0

Χ 4 - Χ 3 –7 Χ – 3 = Χ 4 + (α + γ ) Χ 3 + (σι + ΕΝΑ ντο + ρε ) Χ 2 + (Ενα δ + προ ΧΡΙΣΤΟΥ ) x+ + βδ

Εξίσωση των συντελεστών στο Χ 3 , Χ 2 , Χκαι δωρεάν όρους, παίρνουμε το σύστημα

α + γ = -1

σι + ΕΝΑ ντο + ρε = 0

Ενα δ + προ ΧΡΙΣΤΟΥ = -7

βδ = -3, από όπου βρίσκουμε:ΕΝΑ = -2 ; σι = - 1 ;

Με = 1 ; ρε = 3 .

Έτσι Χ 4 - Χ 3 –7Χ– 3 = (Χ 2 – 2 Χ – 1)(Χ 2 + Χ + 3) = 0 ,

Χ 2 – 2 Χ– 1 = 0 ή Χ 2 + Χ + 3 = 0

Χ 1,2 =
χωρίς ρίζες.

Παρόμοια έχουμε

Χ 4 – 12Χ – 5 = (Χ 2 – 2 Χ – 1)(Χ 2 + 2Χ + 5) = 0 ,

που Χ 2 + 2 Χ + 5 = 0 , ρε = - 16 < 0 , нет корней.

Απάντηση: Χ 1,2 =

Πρόβλημα 6. Λύστε την εξίσωση

= 10.

Λύση. Για να λύσετε αυτή την εξίσωση πρέπει να επιλέξετε αριθμούςΕΝΑΚαι σι ώστε οι αριθμητές και των δύο κλασμάτων να είναι ίδιοι. Επομένως, έχουμε το σύστημα:

= 0 , Χ 0; -1 ; -

= - 10

Έτσι, το καθήκον είναι να βρείτε τους αριθμούςΕΝΑΚαι σι , για την οποία ισχύει η ισότητα

(ένα + 6) Χ 2 + αχ - 5 = Χ 2 + (5 + 2 σι ) Χ + σι

Τώρα, σύμφωνα με το θεώρημα για την ισότητα των πολυωνύμων, είναι απαραίτητο η δεξιά πλευρά αυτής της ισότητας να μετατραπεί στο ίδιο πολυώνυμο που βρίσκεται στην αριστερή πλευρά.

Πρέπει δηλαδή να ικανοποιηθούν οι σχέσεις

ένα + 6 = 1

ΕΝΑ = 5 + 2 σι

– 5 = σι , από όπου βρίσκουμε τις τιμέςΕΝΑ = - 5 ;

σι = - 5 .

Σε αυτές τις αξίεςΕΝΑΚαι σι ισότητα ΕΝΑ + σι = - 10 είναι επίσης δίκαιο.

= 0 , Χ 0; -1 ; -

= 0 ,

= 0 ,

(Χ 2 – 5Χ– 5)(Χ 2 + 3Χ + 1) = 0 ,

Χ 2 – 5Χ– 5 = 0 ή Χ 2 + 3Χ + 1 = 0 ,

Χ 1,2 =
, Χ 3,4 =

Απάντηση: Χ 1,2 =
, Χ 3,4 =

Πρόβλημα 7. Λύστε την εξίσωση

= 4

Λύση. Αυτή η εξίσωση είναι πιο σύνθετη από τις προηγούμενες και επομένως θα την ομαδοποιήσουμε ως εξής: Χ 0;-1;3;-8;12

0 ,

= - 4.

Από την συνθήκη ισότητας δύο πολυωνύμων

Ω 2 + (ένα + 6) Χ + 12 = Χ 2 + (σι + 11) Χ – 3 σι ,

παίρνουμε και λύνουμε ένα σύστημα εξισώσεων για άγνωστους συντελεστέςΕΝΑΚαι σι :

ΕΝΑ = 1

ένα + 6 = σι + 11

12 = – 3 σι , που α = 1 , σι = - 4 .

Πολυώνυμα - 3 – 6Χ + cx 2 + 8 cxΚαι Χ 2 + 21 + 12 ρε – dx είναι ίσα μεταξύ τους πανομοιότυπα μόνο όταν

Με = 1

8 Με - 6 = - ρε

3 = 21 + 12 ρε , Με = 1 , ρε = - 2 .

Με αξίεςα = 1 , σι = - 4 , Με = 1 , ρε = - 2

ισότητα
= - 4 είναι σωστό.

Ως αποτέλεσμα, αυτή η εξίσωση παίρνει την ακόλουθη μορφή:

= 0 ή
= 0 ή
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

Από τα παραδείγματα που εξετάστηκαν, είναι σαφές πώς η επιδέξια χρήση της μεθόδου των αόριστων συντελεστών,

βοηθά στην απλοποίηση της λύσης μιας μάλλον περίπλοκης, ασυνήθιστης εξίσωσης.

2.4. Λειτουργικές εξισώσεις.

«Ο υψηλότερος σκοπός των μαθηματικών... είναι

είναι να βρείτε την κρυφή σειρά σε

χάος που μας περιβάλλει»

N. Viner

Οι συναρτησιακές εξισώσεις είναι μια πολύ γενική κατηγορία εξισώσεων στις οποίες η άγνωστη συνάρτηση είναι μια ορισμένη συνάρτηση. Μια συναρτησιακή εξίσωση με τη στενή έννοια της λέξης νοείται ως εξισώσεις στις οποίες οι επιθυμητές συναρτήσεις σχετίζονται με γνωστές συναρτήσεις μιας ή περισσότερων μεταβλητών χρησιμοποιώντας τη λειτουργία σχηματισμού μιγαδικής συνάρτησης. Μια συναρτησιακή εξίσωση μπορεί επίσης να θεωρηθεί ως έκφραση μιας ιδιότητας που χαρακτηρίζει μια συγκεκριμένη κατηγορία συναρτήσεων

[για παράδειγμα, συναρτητική εξίσωση φά ( Χ ) = φά (- Χ ) χαρακτηρίζει την κλάση των άρτιων συναρτήσεων, τη συναρτησιακή εξίσωσηφά (Χ + 1) = φά (Χ ) – κατηγορία συναρτήσεων με περίοδο 1, κ.λπ.].

Μία από τις απλούστερες συναρτησιακές εξισώσεις είναι η εξίσωσηφά (Χ + y ) = φά (Χ ) + φά (y ). Οι συνεχείς λύσεις αυτής της συναρτησιακής εξίσωσης έχουν τη μορφή

φά (Χ ) = ντοΧ . Ωστόσο, στην κατηγορία των ασυνεχών συναρτήσεων αυτή η συναρτησιακή εξίσωση έχει άλλες λύσεις. Συσχετίζονται με την εξεταζόμενη συναρτησιακή εξίσωση

φά (Χ + y ) = φά (Χ ) · φά (y ), φά (Χ y ) = φά (Χ ) + φά (y ), φά (Χ y ) = φά (Χ )· φά (y ),

συνεχείς λύσεις, που αντίστοιχα έχουν τη μορφή

μι cx , ΜΕlnΧ , Χ α (Χ > 0).

Έτσι, αυτές οι συναρτησιακές εξισώσεις μπορούν να χρησιμοποιηθούν για τον ορισμό εκθετικών, λογαριθμικών και συναρτήσεων ισχύος.

Οι πιο ευρέως χρησιμοποιούμενες εξισώσεις είναι αυτές σε μιγαδικές συναρτήσεις στις οποίες οι απαιτούμενες συναρτήσεις είναι εξωτερικές συναρτήσεις. Θεωρητικές και πρακτικές εφαρμογές

Αυτές ακριβώς οι εξισώσεις ώθησαν εξαιρετικούς μαθηματικούς να τις μελετήσουν.

Για παράδειγμα, στοευθυγραμμία

φά 2 (Χ) = φά (Χ - y)· φά (Χ + y)

N.I.Lobachevskyπου χρησιμοποιείται κατά τον προσδιορισμό της γωνίας παραλληλισμού στη γεωμετρία μου.

Τα τελευταία χρόνια, προβλήματα που σχετίζονται με την επίλυση συναρτησιακών εξισώσεων προσφέρονται αρκετά συχνά σε μαθηματικές Ολυμπιάδες. Η επίλυσή τους δεν απαιτεί γνώσεις πέρα ​​από το εύρος του προγράμματος σπουδών των μαθηματικών στη δευτεροβάθμια εκπαίδευση. Ωστόσο, η επίλυση συναρτησιακών εξισώσεων συχνά προκαλεί ορισμένες δυσκολίες.

Ένας από τους τρόπους εύρεσης λύσεων σε συναρτησιακές εξισώσεις είναι η μέθοδος των αόριστων συντελεστών. Μπορεί να χρησιμοποιηθεί όταν η γενική μορφή της επιθυμητής συνάρτησης μπορεί να προσδιοριστεί από την εμφάνιση της εξίσωσης. Αυτό ισχύει, πρώτα απ 'όλα, για εκείνες τις περιπτώσεις όπου οι λύσεις σε εξισώσεις πρέπει να αναζητηθούν μεταξύ ακέραιων ή κλασματικών ορθολογικών συναρτήσεων.

Ας περιγράψουμε την ουσία αυτής της τεχνικής λύνοντας τα ακόλουθα προβλήματα.

Εργασία 8. Λειτουργίαφά (Χ ) ορίζεται για όλα τα πραγματικά x και ικανοποιεί για όλαΧ R κατάσταση

3 φά(Χ) - 2 φά(1- Χ) = Χ 2 .

Εύρημαφά (Χ ).

Λύση. Αφού στην αριστερή πλευρά αυτής της εξίσωσης πάνω από την ανεξάρτητη μεταβλητή x και τις τιμές της συνάρτησηςφά Εκτελούνται μόνο γραμμικές πράξεις και η δεξιά πλευρά της εξίσωσης είναι μια τετραγωνική συνάρτηση, τότε είναι φυσικό να υποθέσουμε ότι η επιθυμητή συνάρτηση είναι επίσης τετραγωνική:

φά (Χ) = τσεκούρι 2 + bx + ντο , Οπουένα, σι, ντο – συντελεστές που θα καθοριστούν, δηλαδή αβέβαιοι συντελεστές.

Αντικαθιστώντας τη συνάρτηση στην εξίσωση, καταλήγουμε στην ταυτότητα:

3(τσεκούρι 2 + bx+ γ) – 2(ένα(1 – Χ) 2 + σι(1 – Χ) + ντο) = Χ 2 .

τσεκούρι 2 + (5 σι + 4 ένα) Χ + (ντο – 2 ένα – 2 σι) = Χ 2 .

Δύο πολυώνυμα θα είναι πανομοιότυπα ίσα αν είναι ίσα

συντελεστές για τις ίδιες δυνάμεις της μεταβλητής:

ένα = 1

5σι + 4ένα = 0

ντο– 2 ένα – 2 σι = 0.

Από αυτό το σύστημα βρίσκουμε τους συντελεστές

ένα = 1 , σι = - , γ = , Επίσηςικανοποιείισότητα

3 φά (Χ ) - 2 φά (1- Χ ) = Χ 2 στο σύνολο όλων των πραγματικών αριθμών. Ταυτόχρονα, υπάρχει και τέτοιοΧ 0 Εργασία 9. Λειτουργίαy =φά(Χ) για όλα το x ορίζεται, συνεχίζεται και ικανοποιεί την συνθήκηφά (φά (Χ)) – φά(Χ) = 1 + 2 Χ . Βρείτε δύο τέτοιες συναρτήσεις.

Λύση. Εκτελούνται δύο ενέργειες στην επιθυμητή συνάρτηση - η λειτουργία σύνθεσης μιας σύνθετης συνάρτησης και

αφαίρεση. Λαμβάνοντας υπόψη ότι η δεξιά πλευρά της εξίσωσης είναι μια γραμμική συνάρτηση, είναι φυσικό να υποθέσουμε ότι η επιθυμητή συνάρτηση είναι επίσης γραμμική:φά(Χ) = αχ +σι , ΟπουΕΝΑ Καισι – αβέβαιοι συντελεστές. Αντικατάσταση αυτής της συνάρτησης σεφά (φά ( (Χ ) = - Χ - 1 ;

φά 2 (Χ ) = 2 Χ+ , που είναι λύσεις της συναρτησιακής εξίσωσηςφά (φά (Χ)) – φά(Χ) = 1 + 2 Χ .

Συμπέρασμα.

Συμπερασματικά, θα πρέπει να σημειωθεί ότι αυτή η εργασία σίγουρα θα συμβάλει στην περαιτέρω μελέτη μιας πρωτότυπης και αποτελεσματικής μεθόδου επίλυσης ποικίλων μαθηματικών προβλημάτων, τα οποία είναι προβλήματα αυξημένης δυσκολίας και απαιτούν βαθιά γνώση του σχολικού μαθήματος των μαθηματικών και υψηλή λογική Όποιος θέλει να εμβαθύνει ανεξάρτητα τις γνώσεις του στα μαθηματικά, θα βρει επίσης Αυτή η εργασία περιέχει υλικό για προβληματισμό και ενδιαφέρουσες εργασίες, η λύση των οποίων θα φέρει όφελος και ικανοποίηση.

Η εργασία, στο πλαίσιο του υπάρχοντος σχολικού προγράμματος και σε μορφή προσβάσιμη για αποτελεσματική αντίληψη, καθορίζει τη μέθοδο των αόριστων συντελεστών, που βοηθά στην εμβάθυνση του σχολικού μαθήματος στα μαθηματικά.

Φυσικά, όλες οι δυνατότητες της μεθόδου των αόριστων συντελεστών δεν μπορούν να αποδειχθούν σε μια εργασία. Στην πραγματικότητα, η μέθοδος απαιτεί ακόμη περαιτέρω μελέτη και έρευνα.

Κατάλογος χρησιμοποιημένης βιβλιογραφίας.

Glazer G.I..Ιστορία των μαθηματικών στο σχολείο.-Μ.: Εκπαίδευση, 1983.

Gomonov S.A. Λειτουργικές εξισώσεις σε σχολικό μάθημα μαθηματικών // Τα μαθηματικά στο σχολείο. – 2000. –№10 .

Dorofeev G.V., Potapov M.K., Rozov N.H.. Εγχειρίδιο για τα μαθηματικά - M.: Nauka, 1972.

Kurosh A.G. Αλγεβρικές εξισώσεις αυθαίρετων βαθμών - M.: Nauka, 1983.

Likhtarnikov L.M.. Στοιχειώδης εισαγωγή στις συναρτησιακές εξισώσεις. - Αγία Πετρούπολη. : Lan, 1997.

Manturov O.V., Solntsev Yu.K., Sorokin Yu.I., Fedin N.G.. Επεξηγηματικό λεξικό μαθηματικών όρων.-Μ.: Εκπαίδευση, 1971

Modenov V.P.. Εγχειρίδιο για τα μαθηματικά. Μέρος 1.-Μ.: Κρατικό Πανεπιστήμιο της Μόσχας, 1977.

Modenov V.P.. Προβλήματα με παραμέτρους - M.: Εξέταση, 2006.

Potapov M.K., Aleksandrov V.V., Pasichenko P.I.. Άλγεβρα και ανάλυση στοιχειωδών συναρτήσεων - M.: Nauka, 1980.

Khaliullin A.A.. Μπορείτε να το λύσετε ευκολότερα // Μαθηματικά στο σχολείο. – 2003 . - №8 .

Χαλιούλιν.

4. Αναπτύξτε το πολυώνυμο 2Χ 4 – 5Χ 3 + 9Χ 2 – 5Χ+ 3 για πολλαπλασιαστές με ακέραιους συντελεστές.

5. Σε ποια τιμή ΕΝΑ Χ 3 + 6Χ 2 + Ω+ 12 ανά Χ+ 4 ?

6. Σε ποια τιμή της παραμέτρουΕΝΑ την εξίσωσηΧ 3 +5 Χ 2 + + Ω + σι = 0 με ακέραιους συντελεστές έχει δύο διαφορετικές ρίζες, η μία από τις οποίες είναι 1 ?

7. Μεταξύ των ριζών του πολυωνύμου Χ 4 + Χ 3 – 18Χ 2 + Ω + σι με ακέραιους συντελεστές υπάρχουν τρεις ίσοι ακέραιοι αριθμοί. Βρείτε την τιμή σι .

8. Βρείτε τη μεγαλύτερη ακέραια τιμή της παραμέτρου ΕΝΑ,στην οποία η εξίσωση Χ 3 – 8Χ 2 + αχ +σι = 0 με ακέραιους συντελεστές έχει τρεις διαφορετικές ρίζες, η μία από τις οποίες είναι ίση με 2.

9. Σε ποιες τιμές ΕΝΑΚαι σι διαίρεση γίνεται χωρίς υπόλοιπο Χ 4 + 3Χ 3 – 2Χ 2 + Ω + σι επί Χ 2 – 3Χ + 2 ?

10. Πολυώνυμα παραγόντων:

ΕΝΑ)Χ 4 + 2 Χ 2 – Χ + 2 V)Χ 4 – 4Χ 3 +9Χ 2 –8Χ + 5 ρε)Χ 4 + 12Χ – 5

σι)Χ 4 + 3Χ 2 + 2Χ + 3 ΣΟΛ)Χ 4 – 3Χ –2 μι)Χ 4 – 7Χ 2 + 1 .

11. Λύστε τις εξισώσεις:

ΕΝΑ)
= 2 = 2 φά (1 – Χ ) = Χ 2 .

Εύρημα φά (Χ) .

13. Λειτουργία στο= φά (Χ) μπροστά σε όλους Χορίζεται, συνεχίζει και ικανοποιεί την προϋπόθεση φά ( φά (Χ)) = φά (Χ) + Χ.Βρείτε δύο τέτοιες συναρτήσεις.

Ολοκλήρωση κλασματικής-ορθολογικής συνάρτησης.
Μέθοδος αβέβαιου συντελεστή

Συνεχίζουμε να εργαζόμαστε για την ολοκλήρωση κλασμάτων. Έχουμε ήδη εξετάσει ολοκληρώματα ορισμένων τύπων κλασμάτων στο μάθημα και αυτό το μάθημα, κατά μία έννοια, μπορεί να θεωρηθεί συνέχεια. Για να κατανοήσετε με επιτυχία το υλικό, απαιτούνται βασικές δεξιότητες ολοκλήρωσης, οπότε αν μόλις ξεκινήσατε να μελετάτε τα ολοκληρώματα, δηλαδή είστε αρχάριοι, τότε πρέπει να ξεκινήσετε με το άρθρο Αόριστο ολοκλήρωμα. Παραδείγματα λύσεων.

Παραδόξως, τώρα θα ασχοληθούμε όχι τόσο με την εύρεση ολοκληρωμάτων, αλλά... με την επίλυση συστημάτων γραμμικών εξισώσεων. Από αυτή την άποψη επειγόντωςΠροτείνω να παρακολουθήσετε το μάθημα, δηλαδή, πρέπει να είστε καλά γνώστες των μεθόδων αντικατάστασης (μέθοδος «σχολική» και μέθοδος πρόσθεσης (αφαίρεσης) εξισώσεων συστήματος ανά όρο).

Τι είναι μια κλασματική ορθολογική συνάρτηση; Με απλά λόγια, κλασματική-ορθολογική συνάρτηση είναι ένα κλάσμα του οποίου ο αριθμητής και ο παρονομαστής περιέχουν πολυώνυμα ή γινόμενα πολυωνύμων. Επιπλέον, τα κλάσματα είναι πιο εξελιγμένα από αυτά που συζητούνται στο άρθρο Ολοκλήρωση κάποιων κλασμάτων.

Ολοκλήρωση μιας σωστής κλασματικής-ορθολογικής συνάρτησης

Αμέσως ένα παράδειγμα και ένας τυπικός αλγόριθμος για την επίλυση του ολοκληρώματος μιας κλασματικής-ορθολογικής συνάρτησης.

Παράδειγμα 1

Βήμα 1.Το πρώτο πράγμα που κάνουμε ΠΑΝΤΑ όταν λύνουμε ένα ολοκλήρωμα μιας κλασματικής ορθολογικής συνάρτησης είναι να διευκρινίζουμε την ακόλουθη ερώτηση: είναι σωστό το κλάσμα;Αυτό το βήμα εκτελείται προφορικά και τώρα θα εξηγήσω πώς:

Αρχικά κοιτάμε τον αριθμητή και ανακαλύπτουμε ανώτερο πτυχίοπολυώνυμος:

Η κύρια δύναμη του αριθμητή είναι δύο.

Τώρα κοιτάμε τον παρονομαστή και ανακαλύπτουμε ανώτερο πτυχίοπαρονομαστής. Ο προφανής τρόπος είναι να ανοίξετε τις αγκύλες και να φέρετε παρόμοιους όρους, αλλά μπορείτε να το κάνετε πιο απλά, μέσα καθεβρείτε τον υψηλότερο βαθμό σε αγκύλες

και πολλαπλασιάζουμε νοερά: - έτσι, ο υψηλότερος βαθμός του παρονομαστή είναι ίσος με τρία. Είναι προφανές ότι αν ανοίξουμε πραγματικά τις αγκύλες, δεν θα πάρουμε βαθμό μεγαλύτερο από τρεις.

συμπέρασμα: Κύριος βαθμός αριθμητή ΑΥΣΤΗΡΑείναι μικρότερη από την υψηλότερη ισχύ του παρονομαστή, που σημαίνει ότι το κλάσμα είναι σωστό.

Αν σε αυτό το παράδειγμα ο αριθμητής περιείχε το πολυώνυμο 3, 4, 5 κ.λπ. μοίρες, τότε το κλάσμα θα ήταν λανθασμένος.

Τώρα θα εξετάσουμε μόνο τις σωστές κλασματικές ορθολογικές συναρτήσεις. Η περίπτωση που ο βαθμός του αριθμητή είναι μεγαλύτερος ή ίσος με τον βαθμό του παρονομαστή θα συζητηθεί στο τέλος του μαθήματος.

Βήμα 2.Ας παραγοντοποιήσουμε τον παρονομαστή. Ας δούμε τον παρονομαστή μας:

Σε γενικές γραμμές, αυτό είναι ήδη προϊόν παραγόντων, αλλά, ωστόσο, αναρωτιόμαστε: είναι δυνατόν να επεκτείνουμε κάτι άλλο; Το αντικείμενο του βασανισμού θα είναι αναμφίβολα το τετράγωνο τριώνυμο. Επίλυση της δευτεροβάθμιας εξίσωσης:

Η διάκριση είναι μεγαλύτερη από το μηδέν, πράγμα που σημαίνει ότι το τριώνυμο μπορεί πραγματικά να παραγοντοποιηθεί:

Γενικός κανόνας: ΟΛΑ στον παρονομαστή ΜΠΟΡΟΥΝ να συνυπολογιστούν - συντελεστές

Ας αρχίσουμε να διαμορφώνουμε μια λύση:

Βήμα 3.Χρησιμοποιώντας τη μέθοδο των αόριστων συντελεστών, επεκτείνουμε το ολοκλήρωμα σε ένα άθροισμα απλών (στοιχειωδών) κλασμάτων. Τώρα θα είναι πιο ξεκάθαρο.

Ας δούμε τη συνάρτηση ολοκλήρωσης:

Και, ξέρετε, με κάποιο τρόπο αναδύεται μια διαισθητική σκέψη ότι θα ήταν ωραίο να μετατρέψουμε το μεγάλο μας κλάσμα σε πολλά μικρά. Για παράδειγμα, όπως αυτό:

Γεννιέται το ερώτημα, είναι δυνατόν να γίνει αυτό; Ας αναπνεύσουμε με ανακούφιση, λέει το αντίστοιχο θεώρημα της μαθηματικής ανάλυσης – ΕΙΝΑΙ ΔΥΝΑΤΟ. Μια τέτοια αποσύνθεση υπάρχει και είναι μοναδική.

Υπάρχει μόνο ένα πιάσιμο, οι πιθανότητες είναι ΑντίοΔεν ξέρουμε, εξ ου και το όνομα - η μέθοδος των αόριστων συντελεστών.

Όπως μαντέψατε, οι επόμενες κινήσεις του σώματος είναι τέτοιες, μην γελάτε! θα έχει ως στόχο απλώς την ΑΝΑΓΝΩΡΙΣΗ τους - για να μάθετε με τι ισούνται.

Προσοχή, θα σας εξηγήσω αναλυτικά μόνο μια φορά!

Λοιπόν, ας αρχίσουμε να χορεύουμε από:

Στην αριστερή πλευρά μειώνουμε την έκφραση σε έναν κοινό παρονομαστή:

Τώρα μπορούμε με ασφάλεια να απαλλαγούμε από τους παρονομαστές (καθώς είναι οι ίδιοι):

Στην αριστερή πλευρά ανοίγουμε τις αγκύλες, αλλά μην αγγίξετε προς το παρόν τους άγνωστους συντελεστές:

Ταυτόχρονα επαναλαμβάνουμε τον σχολικό κανόνα για τον πολλαπλασιασμό των πολυωνύμων. Όταν ήμουν δάσκαλος, έμαθα να προφέρω αυτόν τον κανόνα με ίσιο πρόσωπο: Για να πολλαπλασιάσετε ένα πολυώνυμο με ένα πολυώνυμο, πρέπει να πολλαπλασιάσετε κάθε όρο ενός πολυωνύμου με κάθε όρο του άλλου πολυωνύμου.

Από την άποψη μιας ξεκάθαρης εξήγησης, είναι καλύτερο να βάλετε τους συντελεστές σε παρενθέσεις (αν και προσωπικά δεν το κάνω ποτέ για να εξοικονομήσω χρόνο):

Συνθέτουμε ένα σύστημα γραμμικών εξισώσεων.
Αρχικά ψάχνουμε για ανώτερα πτυχία:

Και γράφουμε τους αντίστοιχους συντελεστές στην πρώτη εξίσωση του συστήματος:

Θυμηθείτε καλά το ακόλουθο σημείο. Τι θα συνέβαινε αν δεν υπήρχαν καθόλου s στη δεξιά πλευρά; Ας πούμε, θα επιδεικνυόταν απλά χωρίς κανένα τετράγωνο; Στην περίπτωση αυτή, στην εξίσωση του συστήματος θα ήταν απαραίτητο να βάλουμε ένα μηδέν στα δεξιά: . Γιατί μηδέν; Αλλά επειδή στη δεξιά πλευρά μπορείτε πάντα να αντιστοιχίσετε αυτό το ίδιο τετράγωνο με μηδέν: Αν στη δεξιά πλευρά δεν υπάρχουν μεταβλητές ή/και ελεύθερος όρος, τότε βάζουμε μηδενικά στις δεξιές πλευρές των αντίστοιχων εξισώσεων του συστήματος.

Γράφουμε τους αντίστοιχους συντελεστές στη δεύτερη εξίσωση του συστήματος:

Και τέλος, μεταλλικό νερό, επιλέγουμε δωρεάν μέλη.

Ε...έκανα πλάκα. Τα αστεία στην άκρη - τα μαθηματικά είναι μια σοβαρή επιστήμη. Στην ομάδα του ινστιτούτου μας, κανείς δεν γέλασε όταν η επίκουρη καθηγήτρια είπε ότι θα σκορπίσει τους όρους στην αριθμητική γραμμή και θα διάλεγε τους μεγαλύτερους. Ας σοβαρευτούμε. Αν και... όποιος ζει για να δει το τέλος αυτού του μαθήματος, θα χαμογελά ακόμα ήσυχα.

Το σύστημα είναι έτοιμο:

Λύνουμε το σύστημα:

(1) Από την πρώτη εξίσωση εκφράζουμε και την αντικαθιστούμε στη 2η και 3η εξίσωση του συστήματος. Στην πραγματικότητα, ήταν δυνατό να εκφραστεί (ή άλλο γράμμα) από άλλη εξίσωση, αλλά σε αυτή την περίπτωση συμφέρει να εκφραστεί από την 1η εξίσωση, αφού υπάρχει τις μικρότερες πιθανότητες.

(2) Παρουσιάζουμε παρόμοιους όρους στη 2η και 3η εξίσωση.

(3) Προσθέτουμε τη 2η και 3η εξίσωση όρο προς όρο, λαμβάνοντας την ισότητα , από την οποία προκύπτει ότι

(4) Αντικαθιστούμε στη δεύτερη (ή τρίτη) εξίσωση, από όπου βρίσκουμε ότι

(5) Αντικαταστήστε και στην πρώτη εξίσωση, λαμβάνοντας .

Εάν αντιμετωπίζετε δυσκολίες με τις μεθόδους επίλυσης του συστήματος, εξασκήστε τις στην τάξη. Πώς να λύσετε ένα σύστημα γραμμικών εξισώσεων;

Μετά την επίλυση του συστήματος, είναι πάντα χρήσιμο να ελέγξετε - να αντικαταστήσετε τις τιμές που βρέθηκαν κάθεεξίσωση του συστήματος, με αποτέλεσμα όλα να «συγκλίνουν».

Σχεδόν έτοιμο. Βρέθηκαν οι συντελεστές και:

Η τελική εργασία θα πρέπει να μοιάζει κάπως έτσι:

Όπως μπορείτε να δείτε, η κύρια δυσκολία της εργασίας ήταν να συνθέσετε (σωστά!) και να λύσετε (σωστά!) ένα σύστημα γραμμικών εξισώσεων. Και στο τελικό στάδιο, όλα δεν είναι τόσο δύσκολα: χρησιμοποιούμε τις ιδιότητες γραμμικότητας του αόριστου ολοκληρώματος και ολοκληρώνουμε. Σημειώστε ότι κάτω από καθένα από τα τρία ολοκληρώματα έχουμε μια "δωρεάν" σύνθετη συνάρτηση· μίλησα για τα χαρακτηριστικά της ενσωμάτωσής της στο μάθημα Μέθοδος μεταβλητής μεταβολής σε αόριστο ολοκλήρωμα.

Έλεγχος: Διαφοροποιήστε την απάντηση:

Έχει ληφθεί η αρχική συνάρτηση ολοκλήρωσης, πράγμα που σημαίνει ότι το ολοκλήρωμα βρέθηκε σωστά.
Κατά την επαλήθευση, έπρεπε να μειώσουμε την έκφραση σε έναν κοινό παρονομαστή, και αυτό δεν είναι τυχαίο. Η μέθοδος των αόριστων συντελεστών και η αναγωγή μιας έκφρασης σε κοινό παρονομαστή είναι αμοιβαία αντίστροφες ενέργειες.

Παράδειγμα 2

Να βρείτε το αόριστο ολοκλήρωμα.

Ας επιστρέψουμε στο κλάσμα από το πρώτο παράδειγμα: . Είναι εύκολο να παρατηρήσετε ότι στον παρονομαστή όλοι οι παράγοντες είναι ΔΙΑΦΟΡΕΤΙΚΟΙ. Τίθεται το ερώτημα, τι πρέπει να κάνουμε εάν, για παράδειγμα, δοθεί το ακόλουθο κλάσμα: ? Εδώ έχουμε βαθμούς στον παρονομαστή ή, μαθηματικά, πολλαπλάσια. Επιπλέον, υπάρχει ένα τετραγωνικό τριώνυμο που δεν μπορεί να παραγοντοποιηθεί (είναι εύκολο να επαληθευτεί ότι η διάκριση της εξίσωσης είναι αρνητικό, επομένως το τριώνυμο δεν μπορεί να παραγοντοποιηθεί). Τι να κάνω? Η επέκταση σε ένα άθροισμα στοιχειωδών κλασμάτων θα μοιάζει κάπως με άγνωστους συντελεστές στην κορυφή ή κάτι άλλο;

Παράδειγμα 3

Εισαγάγετε μια συνάρτηση

Βήμα 1.Ελέγχοντας αν έχουμε σωστό κλάσμα
Κύριος αριθμητής: 2
Ανώτατος βαθμός παρονομαστή: 8
, που σημαίνει ότι το κλάσμα είναι σωστό.

Βήμα 2.Είναι δυνατόν να συνυπολογίσουμε κάτι στον παρονομαστή; Προφανώς όχι, όλα έχουν ήδη διαμορφωθεί. Το τετράγωνο τριώνυμο δεν μπορεί να επεκταθεί σε προϊόν για τους λόγους που αναφέρθηκαν παραπάνω. Κουκούλα. Λιγότερη δουλειά.

Βήμα 3.Ας φανταστούμε μια κλασματική-ορθολογική συνάρτηση ως άθροισμα στοιχειωδών κλασμάτων.
Σε αυτήν την περίπτωση, η επέκταση έχει την ακόλουθη μορφή:

Ας δούμε τον παρονομαστή μας:
Κατά την αποσύνθεση μιας κλασματικής-ορθολογικής συνάρτησης σε ένα άθροισμα στοιχειωδών κλασμάτων, μπορούν να διακριθούν τρία θεμελιώδη σημεία:

1) Εάν ο παρονομαστής περιέχει έναν παράγοντα «μοναχικό» στην πρώτη δύναμη (στην περίπτωσή μας), τότε βάζουμε έναν αόριστο συντελεστή στην κορυφή (στην περίπτωσή μας). Τα παραδείγματα Νο. 1, 2 αποτελούνταν μόνο από τέτοιους «μοναχικούς» παράγοντες.

2) Αν ο παρονομαστής έχει πολλαπλούςπολλαπλασιαστή, τότε πρέπει να τον αποσυνθέσεις ως εξής:
- δηλαδή, περάστε διαδοχικά όλες τις μοίρες του "Χ" από την πρώτη έως την nη μοίρα. Στο παράδειγμά μας υπάρχουν δύο πολλαπλοί παράγοντες: και , ρίξτε μια άλλη ματιά στην επέκταση που έδωσα και βεβαιωθείτε ότι επεκτείνονται ακριβώς σύμφωνα με αυτόν τον κανόνα.

3) Εάν ο παρονομαστής περιέχει ένα αδιάσπαστο πολυώνυμο του δεύτερου βαθμού (στην περίπτωσή μας), τότε κατά την αποσύνθεση στον αριθμητή πρέπει να γράψετε μια γραμμική συνάρτηση με απροσδιόριστους συντελεστές (στην περίπτωσή μας με απροσδιόριστους συντελεστές και ).

Μάλιστα, υπάρχει και άλλη 4η περίπτωση, αλλά θα το σιωπήσω, αφού στην πράξη είναι εξαιρετικά σπάνιο.

Παράδειγμα 4

Εισαγάγετε μια συνάρτηση ως άθροισμα στοιχειωδών κλασμάτων με άγνωστους συντελεστές.

Αυτό είναι ένα παράδειγμα για να το λύσετε μόνοι σας. Πλήρης λύση και απάντηση στο τέλος του μαθήματος.
Ακολουθήστε τον αλγόριθμο αυστηρά!

Εάν κατανοείτε τις αρχές με τις οποίες πρέπει να επεκτείνετε μια κλασματική-ορθολογική συνάρτηση σε άθροισμα, μπορείτε να μασήσετε σχεδόν οποιοδήποτε ολοκλήρωμα του υπό εξέταση τύπου.

Παράδειγμα 5

Να βρείτε το αόριστο ολοκλήρωμα.

Βήμα 1.Προφανώς το κλάσμα είναι σωστό:

Βήμα 2.Είναι δυνατόν να συνυπολογίσουμε κάτι στον παρονομαστή; Μπορώ. Εδώ είναι το άθροισμα των κύβων . Υπολογίστε τον παρονομαστή χρησιμοποιώντας τον συντομευμένο τύπο πολλαπλασιασμού

Βήμα 3.Χρησιμοποιώντας τη μέθοδο των αόριστων συντελεστών, επεκτείνουμε το ολοκλήρωμα σε ένα άθροισμα στοιχειωδών κλασμάτων:

Λάβετε υπόψη ότι το πολυώνυμο δεν μπορεί να παραγοντοποιηθεί (ελέγξτε ότι η διάκριση είναι αρνητική), οπότε στο επάνω μέρος βάζουμε μια γραμμική συνάρτηση με άγνωστους συντελεστές και όχι μόνο ένα γράμμα.

Φέρνουμε το κλάσμα σε κοινό παρονομαστή:

Ας συνθέσουμε και λύσουμε το σύστημα:

(1) Εκφράζουμε από την πρώτη εξίσωση και την αντικαθιστούμε στη δεύτερη εξίσωση του συστήματος (αυτός είναι ο πιο ορθολογικός τρόπος).

(2) Παρουσιάζουμε παρόμοιους όρους στη δεύτερη εξίσωση.

(3) Προσθέτουμε τη δεύτερη και την τρίτη εξίσωση του συστήματος όρο προς όρο.

Όλοι οι περαιτέρω υπολογισμοί είναι, κατ' αρχήν, προφορικοί, καθώς το σύστημα είναι απλό.

(1) Καταγράφουμε το άθροισμα των κλασμάτων σύμφωνα με τους συντελεστές που βρέθηκαν.

(2) Χρησιμοποιούμε τις ιδιότητες γραμμικότητας του αόριστου ολοκληρώματος. Τι έγινε στο δεύτερο ολοκλήρωμα; Μπορείτε να εξοικειωθείτε με αυτή τη μέθοδο στην τελευταία παράγραφο του μαθήματος. Ολοκλήρωση κάποιων κλασμάτων.

(3) Για άλλη μια φορά χρησιμοποιούμε τις ιδιότητες της γραμμικότητας. Στο τρίτο ολοκλήρωμα αρχίζουμε να απομονώνουμε το πλήρες τετράγωνο (προτελευταία παράγραφος του μαθήματος Ολοκλήρωση κάποιων κλασμάτων).

(4) Παίρνουμε το δεύτερο ολοκλήρωμα, στο τρίτο επιλέγουμε το πλήρες τετράγωνο.

(5) Πάρτε το τρίτο ολοκλήρωμα. Ετοιμος.