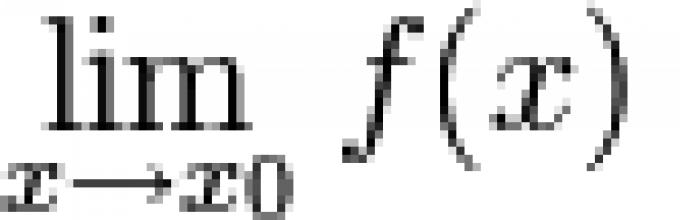Είναι η συνάρτηση απειροελάχιστη στο. Ορισμός μιας απείρως μεγάλης συνάρτησης. Καθορισμός περιορισμένης ακολουθίας

Λογισμός απειρομικρών και μεγάλων

Απειροελάχιστος λογισμός- υπολογισμοί που εκτελούνται με απειροελάχιστα μεγέθη, στους οποίους το παραγόμενο αποτέλεσμα θεωρείται ως άπειρο άθροισμα απειροελάχιστων. Ο λογισμός των απειροελάχιστων είναι μια γενική έννοια για διαφορικό και ολοκληρωτικό λογισμό, που αποτελεί τη βάση των σύγχρονων ανώτερων μαθηματικών. Η έννοια της απειροελάχιστης ποσότητας συνδέεται στενά με την έννοια του ορίου.

Απειροελάχιστος

Ακολουθία ένα nπου ονομάζεται απειροελάχιστος, Αν . Για παράδειγμα, μια ακολουθία αριθμών είναι απειροελάχιστη.

Η συνάρτηση καλείται απειροελάχιστο στην περιοχή ενός σημείου Χ 0 αν .

Η συνάρτηση καλείται απειροελάχιστο στο άπειρο, Αν ή .

Επίσης απειροελάχιστη είναι μια συνάρτηση που είναι η διαφορά μεταξύ μιας συνάρτησης και του ορίου της, δηλαδή αν , Οτι φά(Χ) − ένα = α( Χ) , .

Απεριόριστα μεγάλη ποσότητα

Σε όλους τους παρακάτω τύπους, το άπειρο στα δεξιά της ισότητας υπονοείται ότι έχει ένα ορισμένο πρόσημο (είτε «συν» ή «μείον»). Δηλαδή, για παράδειγμα, η συνάρτηση Χαμαρτία Χ, απεριόριστο και στις δύο πλευρές, δεν είναι απείρως μεγάλο στο .

Ακολουθία ένα nπου ονομάζεται απείρως μεγάλο, Αν .

Η συνάρτηση καλείται απείρως μεγάλος κοντά σε ένα σημείο Χ 0 αν .

Η συνάρτηση καλείται απείρως μεγάλο στο άπειρο, Αν ή .

Ιδιότητες απείρως μικρού και απείρως μεγάλου

Σύγκριση απειροελάχιστων

Πώς να συγκρίνετε απειροελάχιστες ποσότητες;
Ο λόγος των απειροελάχιστων μεγεθών σχηματίζει τη λεγόμενη αβεβαιότητα.

Ορισμοί

Ας υποθέσουμε ότι έχουμε απειροελάχιστες τιμές α( Χ) και β( Χ) (ή, που δεν είναι σημαντικό για τον ορισμό, απειροελάχιστες ακολουθίες).

Για τον υπολογισμό τέτοιων ορίων είναι βολικό να χρησιμοποιήσετε τον κανόνα του L'Hopital.

Παραδείγματα σύγκρισης

Χρησιμοποιώντας ΣΧΕΤΙΚΑ ΜΕ-συμβολισμός, τα αποτελέσματα που προκύπτουν μπορούν να γραφτούν με την ακόλουθη μορφή Χ 5 = ο(Χ 3). Σε αυτήν την περίπτωση, οι ακόλουθες καταχωρήσεις είναι αληθείς: 2Χ 2 + 6Χ = Ο(Χ) Και Χ = Ο(2Χ 2 + 6Χ).

Ισοδύναμες τιμές

Ορισμός

Αν , τότε λέγονται τα απειροελάχιστα μεγέθη α και β ισοδύναμος ().
Είναι προφανές ότι οι ισοδύναμες ποσότητες είναι μια ειδική περίπτωση απειροελάχιστων ποσοτήτων ίδιας τάξης μικρότητας.

Όταν ισχύουν οι ακόλουθες σχέσεις ισοδυναμίας (ως συνέπειες των λεγόμενων αξιοσημείωτων ορίων):

Θεώρημα

Το όριο του πηλίκου (λόγος) δύο απειροελάχιστων μεγεθών δεν θα αλλάξει εάν ένα από αυτά (ή και τα δύο) αντικατασταθεί από μια ισοδύναμη ποσότητα.

Αυτό το θεώρημα έχει πρακτική σημασία κατά την εύρεση ορίων (βλ. παράδειγμα).

Παράδειγμα χρήσης

Αντικατάσταση μικρόΕγώn 2Χ ισοδύναμη τιμή 2 Χ, παίρνουμε

Ιστορικό σκίτσο

Η έννοια του «απειροελάχιστου» συζητήθηκε στην αρχαιότητα σε σχέση με την έννοια των αδιαίρετων ατόμων, αλλά δεν συμπεριλήφθηκε στα κλασικά μαθηματικά. Αναβίωσε ξανά με την εμφάνιση της «μεθόδου των αδιαιρέτων» τον 16ο αιώνα - χωρίζοντας το υπό μελέτη σχήμα σε απειροελάχιστα τμήματα.

Τον 17ο αιώνα έγινε η αλγεβροποίηση του απειροελάχιστου λογισμού. Άρχισαν να ορίζονται ως αριθμητικά μεγέθη που είναι λιγότερα από οποιαδήποτε πεπερασμένη (μη μηδενική) ποσότητα και όμως δεν είναι ίσα με το μηδέν. Η τέχνη της ανάλυσης συνίστατο στη σύνταξη μιας σχέσης που περιέχει απειροελάχιστα (διαφορικά) και στη συνέχεια στην ολοκλήρωσή της.

Οι μαθηματικοί της παλιάς σχολής δοκίμασαν την έννοια απειροελάχιστοςσκληρή κριτική. Ο Michel Rolle έγραψε ότι ο νέος λογισμός είναι " σύνολο έξυπνων λαθών"; Ο Βολταίρος παρατήρησε καυστικά ότι ο λογισμός είναι η τέχνη του υπολογισμού και της ακριβούς μέτρησης πραγμάτων των οποίων η ύπαρξη δεν μπορεί να αποδειχθεί. Ακόμη και ο Huygens παραδέχτηκε ότι δεν καταλάβαινε την έννοια των διαφορικών ανώτερων τάξεων.

Ως ειρωνεία της μοίρας, μπορεί κανείς να θεωρήσει την εμφάνιση στα μέσα του αιώνα μιας μη τυπικής ανάλυσης, η οποία απέδειξε ότι η αρχική άποψη - τα πραγματικά απειροελάχιστα - ήταν επίσης συνεπής και θα μπορούσε να χρησιμοποιηθεί ως βάση για ανάλυση.

δείτε επίσης

Ίδρυμα Wikimedia. 2010.

Δείτε τι είναι η "Απειρομικρή ποσότητα" σε άλλα λεξικά:

ΑΠΕΙΡΩΣ ΜΙΚΡΗ ΠΟΣΟΤΗΤΑ- μια μεταβλητή ποσότητα σε μια συγκεκριμένη διαδικασία, αν σε αυτή τη διαδικασία πλησιάζει (τείνει) άπειρα στο μηδέν... Μεγάλη Πολυτεχνική Εγκυκλοπαίδεια

Απειροελάχιστος- ■ Κάτι άγνωστο, αλλά σχετικό με την ομοιοπαθητική... Λεξικό κοινών αληθειών

Λειτουργία y=f(x)που ονομάζεται απειροελάχιστοςστο x→aή πότε Χ→∞, εάν ή , δηλ. μια απειροελάχιστη συνάρτηση είναι μια συνάρτηση της οποίας το όριο σε ένα δεδομένο σημείο είναι μηδέν.

Παραδείγματα.

1. Λειτουργία f(x)=(Χ-1) Το 2 είναι απειροελάχιστο στο Χ→1, αφού (βλ. σχήμα).

2. Λειτουργία f(x)= tg Χ– απειροελάχιστο στο Χ→0.

3. f(x)= log(1+ Χ) – απειροελάχιστο στο Χ→0.

4. f(x) = 1/Χ– απειροελάχιστο στο Χ→∞.

Ας δημιουργήσουμε την ακόλουθη σημαντική σχέση:

Θεώρημα.Εάν η συνάρτηση y=f(x)αντιπροσωπεύσιμο με x→aως άθροισμα ενός σταθερού αριθμού σικαι απειροελάχιστο μέγεθος α(x): f (x)=b+ α(x)Οτι .

Αντίθετα, αν , τότε f (x)=b+α(x), Οπου τσεκούρι)– απειροελάχιστο στο x→a.

Απόδειξη.

1. Ας αποδείξουμε το πρώτο μέρος της δήλωσης. Από την ισότητα f(x)=b+α(x)πρέπει |f(x) – b|=| α|. Αλλά από τότε τσεκούρι)είναι απειροελάχιστο, τότε για το αυθαίρετο ε υπάρχει δ – μια γειτονιά του σημείου ένα,μπροστά σε όλους Χαπό το οποίο, αξίες τσεκούρι)ικανοποιήσει τη σχέση |α(x)|< ε. Επειτα |f(x) – b|< ε. Και αυτό σημαίνει ότι.

2. Αν , τότε για οποιαδήποτε ε >0 για όλα Χαπό κάποια δ – γειτονιά ενός σημείου έναθα |f(x) – b|< ε. Αν όμως υποδηλώσουμε f(x) – b= α, Οτι |α(x)|< ε, που σημαίνει ότι ένα– απειροελάχιστο.

Ας εξετάσουμε τις βασικές ιδιότητες των απειροελάχιστων συναρτήσεων.

Θεώρημα 1.Το αλγεβρικό άθροισμα δύο, τριών και γενικά οποιουδήποτε πεπερασμένου αριθμού απειροελάχιστων είναι απειροελάχιστη συνάρτηση.

Απόδειξη. Ας δώσουμε μια απόδειξη για δύο όρους. Αφήνω f(x)=α(x)+β(x), πού και . Πρέπει να αποδείξουμε ότι για αυθαίρετα αυθαίρετα μικρά ε > 0 βρέθηκαν δ> 0, έτσι ώστε για Χ, ικανοποιώντας την ανισότητα |x – a|<δ , εκτελέστηκε |f(x)|< ε.

Λοιπόν, ας διορθώσουμε έναν αυθαίρετο αριθμό ε > 0. Αφού σύμφωνα με τις προϋποθέσεις του θεωρήματος α(x)είναι μια απειροελάχιστη συνάρτηση, τότε υπάρχει μια τέτοια δ 1 > 0, που είναι |x – a|< δ 1 έχουμε |α(x)|< ε / 2. Ομοίως, από τότε β(x)είναι απειροελάχιστο, τότε υπάρχει τέτοιο δ 2 > 0, που είναι |x – a|< δ 2 έχουμε | β(x)|< ε / 2.

Ας πάρουμε δ=min(δ 1 , δ2 } .Στη συνέχεια στην περιοχή του σημείου έναακτίνα κύκλου δ καθεμία από τις ανισότητες θα ικανοποιηθεί |α(x)|< ε / 2 και | β(x)|< ε / 2. Επομένως, σε αυτή τη γειτονιά θα υπάρχουν

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

εκείνοι. |f(x)|< ε, που είναι αυτό που έπρεπε να αποδειχθεί.

Θεώρημα 2.Προϊόν μιας απειροελάχιστης συνάρτησης τσεκούρι)για περιορισμένη λειτουργία f(x)στο x→a(ή πότε x→∞) είναι μια απειροελάχιστη συνάρτηση.

Απόδειξη. Από τη λειτουργία f(x)είναι περιορισμένη, τότε υπάρχει αριθμός Μέτσι ώστε για όλες τις αξίες Χαπό κάποια γειτονιά ενός σημείου a|f(x)|≤M.Επιπλέον, από τότε τσεκούρι)είναι απειροελάχιστη συνάρτηση στο x→a, τότε για αυθαίρετο ε > 0 υπάρχει γειτονιά του σημείου ένα, στην οποία θα ισχύει η ανισότητα |α(x)|< ε /Μ. Τότε στη μικρότερη από αυτές τις γειτονιές έχουμε | αf|< ε /Μ= ε. Και αυτό σημαίνει ότι αφ– απειροελάχιστο. Για την περίσταση x→∞η απόδειξη γίνεται με παρόμοιο τρόπο.

Από το αποδεδειγμένο θεώρημα προκύπτει:

Συμπέρασμα 1.Αν και, τότε.

Συμπέρασμα 2.Αν c= const, τότε .

Θεώρημα 3.Λόγος απειροελάχιστης συνάρτησης α(x)ανά λειτουργία f(x), το όριο του οποίου είναι διαφορετικό από το μηδέν, είναι μια απειροελάχιστη συνάρτηση.

Απόδειξη. Αφήστε . Μετά 1 /f(x)υπάρχει περιορισμένη λειτουργία. Επομένως, ένα κλάσμα είναι το γινόμενο μιας απειροελάχιστης συνάρτησης και μιας περιορισμένης συνάρτησης, δηλ. η συνάρτηση είναι απειροελάχιστη.

Def:Η συνάρτηση καλείται απειροελάχιστοςστο , εάν .

Στη σημειογραφία " " θα υποθέσουμε ότι x 0μπορεί να λάβει ως τελική τιμή: x 0= Constκαι άπειρο: x 0= ∞.

Ιδιότητες απειροελάχιστων συναρτήσεων:

1) Το αλγεβρικό άθροισμα ενός πεπερασμένου αριθμού απειροελάχιστων συναρτήσεων είναι ένα απειροελάχιστο άθροισμα συναρτήσεων.

2) Το γινόμενο ενός πεπερασμένου αριθμού απειροελάχιστων συναρτήσεων είναι απειροελάχιστη συνάρτηση.

3) Το γινόμενο μιας περιορισμένης συνάρτησης και μιας απειροελάχιστης συνάρτησης είναι μια απειροελάχιστη συνάρτηση.

4) Το πηλίκο της διαίρεσης μιας απειροελάχιστης συνάρτησης με μια συνάρτηση της οποίας το όριο είναι μη μηδενικό είναι απειροελάχιστη συνάρτηση.

Παράδειγμα: Λειτουργία y = 2 + Χείναι απειροελάχιστο στο , επειδή .

Def:Η συνάρτηση καλείται απείρως μεγάλοστο , εάν .

Ιδιότητες απείρως μεγάλων συναρτήσεων:

1) Το άθροισμα των απείρως μεγάλων συναρτήσεων είναι μια απείρως μεγάλη συνάρτηση.

2) Το γινόμενο μιας απείρως μεγάλης συνάρτησης και μιας συνάρτησης της οποίας το όριο είναι μη μηδενικό είναι μια απείρως μεγάλη συνάρτηση.

3) Το άθροισμα μιας απείρως μεγάλης συνάρτησης και μιας περιορισμένης συνάρτησης είναι μια απείρως μεγάλη συνάρτηση.

4) Το πηλίκο της διαίρεσης μιας απείρως μεγάλης συνάρτησης με μια συνάρτηση που έχει πεπερασμένο όριο είναι μια απείρως μεγάλη συνάρτηση.

Παράδειγμα: Λειτουργία y= είναι απείρως μεγάλο στο , γιατί .

Θεώρημα.Σχέση μεταξύ απείρως μικρών και απείρως μεγάλων ποσοτήτων. Εάν μια συνάρτηση είναι απειροελάχιστη στο , τότε η συνάρτηση είναι απείρως μεγάλη στο . Και αντίστροφα, αν μια συνάρτηση είναι απείρως μεγάλη στο , τότε η συνάρτηση είναι απειροελάχιστη στο .

Η αναλογία δύο απειροελάχιστων συνήθως συμβολίζεται με το σύμβολο και η αναλογία δύο απειρομικρών με το σύμβολο. Και οι δύο σχέσεις είναι αόριστες με την έννοια ότι το όριό τους μπορεί να υπάρχει ή να μην υπάρχει, να είναι ίσο με έναν ορισμένο αριθμό ή να είναι άπειρες, ανάλογα με τον τύπο των συγκεκριμένων συναρτήσεων που περιλαμβάνονται στις αόριστες εκφράσεις.

Εκτός από τις αβεβαιότητες τύπου και τις αβεβαιότητες, οι ακόλουθες εκφράσεις είναι:

Διαφορά απείρως μεγάλων του ίδιου ζωδίου.

Το γινόμενο ενός απειροελάχιστου από ένα απείρως μεγάλο.

Μια εκθετική συνάρτηση της οποίας η βάση τείνει στο 1 και ο εκθέτης τείνει σε ;

Μια εκθετική συνάρτηση της οποίας η βάση είναι απειροελάχιστη και της οποίας ο εκθέτης είναι απείρως μεγάλος.

Μια εκθετική συνάρτηση της οποίας η βάση και ο εκθέτης είναι απειροελάχιστοι.

Μια εκθετική συνάρτηση της οποίας η βάση είναι απείρως μεγάλη και της οποίας ο εκθέτης είναι απειροελάχιστος.

Λέγεται ότι υπάρχει αβεβαιότητα του αντίστοιχου τύπου. Ο υπολογισμός ορίου καλείται σε αυτές τις περιπτώσεις αποκαλύπτοντας την αβεβαιότητα. Για να αποκαλυφθεί η αβεβαιότητα, η έκφραση κάτω από το πρόσημο ορίου μετατρέπεται σε μια μορφή που δεν περιέχει αβεβαιότητα.

Κατά τον υπολογισμό των ορίων, χρησιμοποιούνται οι ιδιότητες των ορίων, καθώς και οι ιδιότητες των απειροελάχιστων και απείρως μεγάλων συναρτήσεων.

Ας δούμε παραδείγματα υπολογισμών διαφόρων ορίων.

1) . 2) .

4) , επειδή γινόμενο μιας απειροελάχιστης συνάρτησης στο και μιας περιορισμένης συνάρτησης είναι απειροελάχιστο.

5) . 6) .

7) = =

. Σε αυτή την περίπτωση, υπήρχε μια αβεβαιότητα τύπου, η οποία επιλύθηκε με την παραγοντοποίηση των πολυωνύμων και την αναγωγή τους σε έναν κοινό παράγοντα.

= .

Σε αυτήν την περίπτωση, υπήρχε μια αβεβαιότητα τύπου , η οποία επιλύθηκε πολλαπλασιάζοντας τον αριθμητή και τον παρονομαστή με την παράσταση, χρησιμοποιώντας τον τύπο και στη συνέχεια μειώνοντας το κλάσμα κατά (+1).

9)
. Σε αυτό το παράδειγμα, η αβεβαιότητα τύπου αποκαλύφθηκε διαιρώντας τον αριθμητή και τον παρονομαστή του κλάσματος με την κύρια ισχύ.

Υπέροχα όρια

Το πρώτο υπέροχο όριο : .

Απόδειξη.Ας εξετάσουμε τον μοναδιαίο κύκλο (Εικ. 3).

Εικ.3. Κύκλος μονάδας

Αφήνω Χ– ακτινικό μέτρο της κεντρικής γωνίας MOA(), Επειτα ΟΑ = R= 1, MK= αμαρτία Χ, ΣΤΟ= tg Χ. Συγκρίνοντας τα εμβαδά των τριγώνων ΟΜΑ, ΟΤΑκαι κλάδους ΟΜΑ, παίρνουμε:

Διαιρέστε την τελευταία ανισότητα με την αμαρτία Χ, παίρνουμε:

Αφού στο , τότε κατά ιδιότητα 5) όρια

Από εδώ προέρχεται η αντίστροφη τιμή, η οποία έπρεπε να αποδειχθεί.

Σχόλιο:Αν η συνάρτηση είναι απειροελάχιστη στο , δηλ. , τότε το πρώτο αξιοσημείωτο όριο έχει τη μορφή:

Ας δούμε παραδείγματα υπολογισμών ορίων χρησιμοποιώντας το πρώτο αξιοσημείωτο όριο.

Κατά τον υπολογισμό αυτού του ορίου, χρησιμοποιήσαμε τον τριγωνομετρικό τύπο: .

Ας δούμε παραδείγματα υπολογισμών ορίων χρησιμοποιώντας το δεύτερο αξιοσημείωτο όριο.

2) .

3) . Υπάρχει αβεβαιότητα τύπου. Ας κάνουμε μια αντικατάσταση, τότε? στο .

Λογισμός απειρομικρών και μεγάλων

Απειροελάχιστος

Η συνάρτηση καλείται απειροελάχιστο στην περιοχή ενός σημείου Χ 0 αν .

Η συνάρτηση καλείται απειροελάχιστο στο άπειρο, Αν ή .

Απεριόριστα μεγάλη ποσότητα

Ακολουθία ένα nπου ονομάζεται απείρως μεγάλο, Αν .

Η συνάρτηση καλείται απείρως μεγάλος κοντά σε ένα σημείο Χ 0 αν .

Η συνάρτηση καλείται απείρως μεγάλο στο άπειρο, Αν ή .

Σε όλες τις περιπτώσεις, το άπειρο προς τα δεξιά της ισότητας υπονοείται ότι έχει ένα ορισμένο πρόσημο (είτε «συν» ή «πλην»). Δηλαδή, για παράδειγμα, η συνάρτηση Χαμαρτία Χδεν είναι απείρως μεγάλο στο .

Ιδιότητες απείρως μικρού και απείρως μεγάλου

Σύγκριση απειροελάχιστων

Ορισμοί

Για τον υπολογισμό τέτοιων ορίων είναι βολικό να χρησιμοποιήσετε τον κανόνα του L'Hopital.

Παραδείγματα σύγκρισης

Ισοδύναμες τιμές

Ορισμός

Όταν ισχύουν οι ακόλουθες σχέσεις ισοδυναμίας: , , .

Θεώρημα

Αυτό το θεώρημα έχει πρακτική σημασία κατά την εύρεση ορίων (βλ. παράδειγμα).

Παράδειγμα χρήσης

Αντικατάσταση μικρόΕγώn 2Χ ισοδύναμη τιμή 2 Χ, παίρνουμε

Ιστορικό σκίτσο

δείτε επίσης

Ίδρυμα Wikimedia. 2010.

Δείτε τι είναι το "Infinitely large" σε άλλα λεξικά:

Η μεταβλητή ποσότητα Υ είναι το αντίστροφο της απειροελάχιστης ποσότητας Χ, δηλαδή Υ = 1/Χ... Μεγάλο Εγκυκλοπαιδικό Λεξικό

Η μεταβλητή y είναι το αντίστροφο του απειροελάχιστου x, δηλαδή y = 1/x. * * * ΑΠΕΙΡΑ ΜΕΓΑΛΟ ΑΠΕΙΡΑ ΜΕΓΑΛΟ, μεταβλητή ποσότητα Υ, αντίστροφη προς την απειροελάχιστη ποσότητα Χ, δηλαδή Υ = 1/Χ ... εγκυκλοπαιδικό λεξικό

Στα μαθηματικά, μια μεταβλητή ποσότητα που, σε μια δεδομένη διαδικασία αλλαγής, γίνεται και παραμένει μεγαλύτερη σε απόλυτη τιμή από οποιονδήποτε προκαθορισμένο αριθμό. Μελέτη Β. β. Οι ποσότητες μπορούν να μειωθούν στη μελέτη των απειροελάχιστων (Βλ.... ... Μεγάλη Σοβιετική Εγκυκλοπαίδεια

Η συνάρτηση καλείται απειροελάχιστο στο
ή πότε
, Αν
ή
.

Για παράδειγμα: λειτουργία
απειροελάχιστο στο
; λειτουργία
απειροελάχιστο στο
.

Σημείωση 1. Χωρίς να υποδεικνύεται η κατεύθυνση αλλαγής του ορίσματος, καμία συνάρτηση δεν μπορεί να ονομαστεί απειροελάχιστη. Ναι, η λειτουργία
στο
είναι απειροελάχιστο, και πότε
δεν είναι πλέον απειροελάχιστο (
).

Σημείωση 2. Από τον ορισμό του ορίου μιας συνάρτησης σε ένα σημείο, για απειροελάχιστες συναρτήσεις ισχύει η ακόλουθη ανισότητα:
Θα χρησιμοποιήσουμε αυτό το γεγονός περισσότερες από μία φορές στο μέλλον.

Ας καθορίσουμε μερικά σημαντικά ιδιότητες απειροελάχιστων συναρτήσεων.

Θεώρημα (σχετικά με τη σύνδεση μιας συνάρτησης, το όριό της και το απειροελάχιστο): Αν η συνάρτηση
μπορεί να αναπαρασταθεί ως άθροισμα ενός σταθερού αριθμού ΕΝΑκαι απειροελάχιστη συνάρτηση
στο
, μετά τον αριθμό

Απόδειξη:

Από τις συνθήκες του θεωρήματος προκύπτει ότι η συνάρτηση
.

Ας εκφραστούμε από εδώ
:
. Από τη λειτουργία
απειροελάχιστη, ισχύει η ανισότητα
, μετά για την έκφραση (
) ισχύει επίσης η ανισότητα

Και αυτό σημαίνει ότι
.

Θεώρημα (αντίστροφα): αν
, μετά η συνάρτηση
μπορεί να αναπαρασταθεί ως το άθροισμα ενός αριθμού ΕΝΑκαι απειροελάχιστο στο
λειτουργίες
, δηλ.
.

Απόδειξη:

Επειδή
, στη συνέχεια για
η ανισότητα ισχύει
(*) Εξετάστε τη συνάρτηση
ως ενιαίο και ξαναγράψτε την ανισότητα (*) στη μορφή

Από την τελευταία ανισότητα προκύπτει ότι η τιμή (
) είναι απειροελάχιστο στο
. Ας το χαρακτηρίσουμε
.

Οπου
. Το θεώρημα είναι αποδεδειγμένο.

Θεώρημα 1 . Το αλγεβρικό άθροισμα ενός πεπερασμένου αριθμού απειροελάχιστων συναρτήσεων είναι μια απειροελάχιστη συνάρτηση.

Απόδειξη:

Ας εκτελέσουμε την απόδειξη για δύο όρους, αφού για κάθε πεπερασμένο αριθμό όρων δίνεται με παρόμοιο τρόπο.

Αφήνω
Και
απειροελάχιστο στο
λειτουργίες και
– το άθροισμα αυτών των συναρτήσεων. Ας το αποδείξουμε για
, υπάρχει κάτι τέτοιο
αυτό είναι για όλους Χ, ικανοποιώντας την ανισότητα
, ισχύει η ανισότητα
.

Από τη λειτουργία
απειροελάχιστη συνάρτηση
αυτό είναι για όλους
η ανισότητα ισχύει
.

Από τη λειτουργία
απειροελάχιστη συνάρτηση
, και επομένως υπάρχει τέτοιο αυτό είναι για όλους
η ανισότητα ισχύει
.

Ας πάρουμε ίσο με τον μικρότερο αριθμό Και , μετά μέσα – γειτονιά του σημείου ΕΝΑοι ανισότητες θα ικανοποιηθούν
,
.

Ας δημιουργήσουμε μια λειτουργική μονάδα
και να αξιολογήσει τη σημασία του.

Αυτό είναι
, τότε η συνάρτηση είναι απειροελάχιστη, κάτι που έπρεπε να αποδειχθεί.

Θεώρημα 2. Προϊόν μιας απειροελάχιστης συνάρτησης
στο
για περιορισμένη λειτουργία
είναι μια απειροελάχιστη συνάρτηση.

Απόδειξη:

Από τη λειτουργία
οριοθετημένο, τότε υπάρχει ένας θετικός αριθμός
αυτό είναι για όλους η ανισότητα ισχύει
.

Από τη λειτουργία
απειροελάχιστο στο
, τότε υπάρχει τέτοιο – γειτονιά ενός σημείου αυτό είναι για όλους σε αυτή τη γειτονιά ισχύει η ανισότητα
.

Εξετάστε τη συνάρτηση
και αξιολογήστε την ενότητα του

Έτσι
, και μετά
– απειροελάχιστο.

Το θεώρημα είναι αποδεδειγμένο.

Θεωρήματα για τα όρια.

Θεώρημα 1. Το όριο ενός αλγεβρικού αθροίσματος ενός πεπερασμένου αριθμού συναρτήσεων είναι ίσο με το αλγεβρικό άθροισμα των ορίων αυτών των συναρτήσεων

Απόδειξη:

Για να το αποδείξουμε, αρκεί να εξετάσουμε δύο λειτουργίες, αυτό δεν θα παραβιάζει τη γενικότητα του συλλογισμού.

Αφήνω
,
.

Σύμφωνα με το θεώρημα για τη σύνδεση μιας συνάρτησης, του ορίου της και μιας απειροελάχιστης συνάρτησης
Και
μπορεί να αναπαρασταθεί στη μορφή
Οπου
Και
– απειροελάχιστο στο
.

Ας βρούμε το άθροισμα των συναρτήσεων
Και

Μέγεθος
υπάρχει σταθερή τιμή
– η ποσότητα είναι απειροελάχιστη. Η συνάρτηση λοιπόν
παρουσιάζεται ως το άθροισμα μιας σταθερής τιμής και μιας απειροελάχιστης συνάρτησης.

Μετά ο αριθμός
είναι το όριο της συνάρτησης
, δηλ.

Το θεώρημα είναι αποδεδειγμένο.

Θεώρημα 2 . Το όριο του γινομένου ενός πεπερασμένου αριθμού συναρτήσεων είναι ίσο με το γινόμενο των ορίων αυτών των συναρτήσεων

Απόδειξη:

Χωρίς να χάσουμε τη γενικότητα του συλλογισμού, θα πραγματοποιήσουμε την απόδειξη για δύο λειτουργίες
Και
.

Ας είναι τότε
,

Ας βρούμε το γινόμενο των συναρτήσεων
Και

Μέγεθος
υπάρχει μια σταθερή ποσότητα, μια απειροελάχιστη συνάρτηση. Επομένως, ο αριθμός
είναι το όριο της συνάρτησης
, δηλαδή η ισότητα είναι αληθινή

Συνέπεια:
.

Θεώρημα 3. Το όριο του πηλίκου δύο συναρτήσεων είναι ίσο με το πηλίκο των ορίων αυτών των συναρτήσεων αν το όριο του παρονομαστή είναι μη μηδενικό

Απόδειξη: Αφήστε
,

Επειτα
,
.

Ας βρούμε το πηλίκο και να εκτελέσετε μερικούς πανομοιότυπους μετασχηματισμούς σε αυτό

Μέγεθος σταθερό, κλάσμα
απείρως μικρό. Επομένως, η συνάρτηση παριστάνεται ως το άθροισμα ενός σταθερού αριθμού και μιας απειροελάχιστης συνάρτησης.

Επειτα
.

Σχόλιο. Τα θεωρήματα 1-3 έχουν αποδειχθεί για την περίπτωση
. Ωστόσο, μπορεί να ισχύουν όταν
, αφού η απόδειξη των θεωρημάτων σε αυτή την περίπτωση πραγματοποιείται ομοίως.

Για παράδειγμα. Βρείτε όρια:

Το πρώτο και το δεύτερο είναι υπέροχα όρια.

Λειτουργία δεν ορίζεται στο
. Ωστόσο, οι τιμές του κοντά στο σημείο μηδέν υπάρχουν. Επομένως, μπορούμε να θεωρήσουμε το όριο αυτής της συνάρτησης στο
. Αυτό το όριο ονομάζεται πρώτα εκπληκτικός όριο .

Μοιάζει:
.

Για παράδειγμα . Βρείτε όρια: 1.
. Ορίζω
, Αν
, Οτι
.
; 2.
. Ας μετατρέψουμε αυτήν την έκφραση έτσι ώστε το όριο να μειωθεί στο πρώτο αξιοσημείωτο όριο.
; 3..

Ας εξετάσουμε μια μεταβλητή της φόρμας
, όπου παίρνει τις τιμές των φυσικών αριθμών με αύξουσα σειρά. Ας δώσουμε διαφορετικές έννοιες: αν

Δίνοντας τις ακόλουθες τιμές από το σετ
, είναι εύκολο να δει κανείς ότι η έκφραση
στο
θα
. Επιπλέον, είναι αποδεδειγμένο ότι
έχει ένα όριο. Αυτό το όριο υποδεικνύεται με το γράμμα :
.

Αριθμός παράλογος:
.

Τώρα εξετάστε το όριο της συνάρτησης
στο
. Αυτό το όριο ονομάζεται δεύτερο αξιοσημείωτο όριο

Μοιάζει
.

Για παράδειγμα.

ΕΝΑ)
. Εκφραση
αντικαταστήστε το με το προϊόν πανομοιότυποι παράγοντες
, εφαρμόζουμε το θεώρημα ορίου προϊόντος και το δεύτερο αξιοσημείωτο όριο. σι)
. Ας βάλουμε
, Επειτα
,
.

Το δεύτερο αξιοσημείωτο όριο χρησιμοποιείται σε πρόβλημα συνεχούς σύνθεσης

Κατά τον υπολογισμό του εισοδήματος σε μετρητά από καταθέσεις, χρησιμοποιείται συχνά ο τύπος του σύνθετου τόκου, ο οποίος μοιάζει με:

Οπου - αρχική συνεισφορά,

- ετήσιοι τραπεζικοί τόκοι,

- αριθμός δεδουλευμένων τόκων ανά έτος,

- χρόνος, σε χρόνια.

Ωστόσο, στις θεωρητικές μελέτες, όταν αιτιολογούν επενδυτικές αποφάσεις, χρησιμοποιούν συχνά τον τύπο του νόμου της εκθετικής (εκθετικής) ανάπτυξης

Ο τύπος για τον νόμο της εκθετικής αύξησης προκύπτει ως αποτέλεσμα της εφαρμογής του δεύτερου αξιοσημείωτου ορίου στον τύπο σύνθετου ενδιαφέροντος

Συνέχεια λειτουργιών.

Εξετάστε τη συνάρτηση
ορίζεται κάποια στιγμή και κάποια γειτονιά του σημείου . Αφήστε τη συνάρτηση να έχει την τιμή στο υποδεικνυόμενο σημείο
.

Ορισμός 1. Λειτουργία
που ονομάζεται συνεχής σε ένα σημείο , εάν ορίζεται σε μια γειτονιά ενός σημείου, συμπεριλαμβανομένου του ίδιου του σημείου και
.

Ο ορισμός της συνέχειας μπορεί να διατυπωθεί διαφορετικά.

Αφήστε τη λειτουργία
ορίζεται σε κάποια τιμή ,
. Αν το επιχείρημα δώστε μια προσαύξηση
, τότε η συνάρτηση θα λάβει μια αύξηση

Αφήστε τη συνάρτηση στο σημείο συνεχής (από τον πρώτο ορισμό της συνέχειας μιας συνάρτησης σε ένα σημείο),

Αν δηλαδή η συνάρτηση είναι συνεχής στο σημείο , τότε μια απειροελάχιστη αύξηση του ορίσματος
σε αυτό το σημείο αντιστοιχεί μια απειροελάχιστη αύξηση της συνάρτησης.

Το αντίστροφο ισχύει επίσης: αν μια απειροελάχιστη αύξηση στο όρισμα αντιστοιχεί σε μια απειροελάχιστη αύξηση στη συνάρτηση, τότε η συνάρτηση είναι συνεχής.

Ορισμός 2. Λειτουργία
ονομάζεται συνεχής στο
(στο σημείο ), αν ορίζεται σε αυτό το σημείο και κάποιο από τα περίχωρά του και αν
.

Λαμβάνοντας υπόψη τον πρώτο και τον δεύτερο ορισμό της συνέχειας μιας συνάρτησης σε ένα σημείο, μπορούμε να λάβουμε την ακόλουθη δήλωση:

ή
, Αλλά
, Επειτα
.

Επομένως, για να βρεθεί το όριο μιας συνεχούς συνάρτησης στο
αρκεί να χρησιμοποιήσουμε μια έκφραση αναλυτικής συνάρτησης αντί για όρισμα αντικαταστήσει την αξία του .

Ορισμός 3. Μια συνάρτηση που είναι συνεχής σε κάθε σημείο μιας συγκεκριμένης περιοχής ονομάζεται συνεχής σε αυτήν την περιοχή.

Για παράδειγμα:

Παράδειγμα 1. Να αποδείξετε ότι η συνάρτηση
είναι συνεχής σε όλα τα σημεία του πεδίου ορισμού.

Ας χρησιμοποιήσουμε τον δεύτερο ορισμό της συνέχειας μιας συνάρτησης σε ένα σημείο. Για να το κάνετε αυτό, λάβετε οποιαδήποτε τιμή του επιχειρήματος και δώστε του μια αύξηση
. Ας βρούμε την αντίστοιχη αύξηση της συνάρτησης

Παράδειγμα 2. Να αποδείξετε ότι η συνάρτηση
συνεχής σε όλα τα σημεία από
.

Ας δώσουμε το επιχείρημα αύξηση
, τότε η συνάρτηση θα αυξηθεί

Ας βρούμε από τη συνάρτηση
, δηλαδή περιορισμένη.

Ομοίως, μπορεί να αποδειχθεί ότι όλες οι βασικές στοιχειώδεις συναρτήσεις είναι συνεχείς σε όλα τα σημεία του πεδίου ορισμού τους, δηλαδή το πεδίο ορισμού μιας στοιχειώδους συνάρτησης συμπίπτει με το πεδίο συνέχειάς της.

Ορισμός 4. Αν η συνάρτηση
συνεχής σε κάθε σημείο κάποιου διαστήματος
, τότε λέμε ότι η συνάρτηση είναι συνεχής σε αυτό το διάστημα.