Ο Νικολάι αγόρασε ένα γενικό σημειωματάριο 96 φύλλων. Μαθηματικές Ολυμπιάδες και Ολυμπιάδες προβλήματα. Σας ευχόμαστε επιτυχία

Ενότητες: Μαθηματικά

Αγαπητέ συμμετέχοντες στην Ολυμπιάδα!

Η Σχολική Μαθηματική Ολυμπιάδα διεξάγεται σε ένα γύρο.
Προσφέρονται 5 προβλήματα διαφόρων επιπέδων δυσκολίας.
Δεν έχετε ιδιαίτερες απαιτήσεις για το σχεδιασμό της εργασίας. Η μορφή παρουσίασης της λύσης προβλημάτων, καθώς και οι μέθοδοι επίλυσης, μπορεί να είναι οποιαδήποτε. Εάν έχετε συγκεκριμένες ιδέες για ένα συγκεκριμένο πρόβλημα, αλλά δεν μπορείτε να φέρετε τη λύση στο τέλος, μη διστάσετε να εκφράσετε όλες τις σκέψεις σας. Ακόμη και μερικώς λυμένα προβλήματα θα αξιολογηθούν με τον αντίστοιχο αριθμό μορίων.
Ξεκινήστε να λύνετε εργασίες που είναι πιο εύκολες κατά τη γνώμη σας και μετά προχωρήστε στις υπόλοιπες. Αυτό θα σας εξοικονομήσει χρόνο εργασίας.

Σας ευχόμαστε επιτυχία!

Σχολικό στάδιο της Πανρωσικής Ολυμπιάδας για μαθητές στα μαθηματικά

Βαθμός 5.

Ασκηση 1. Στην έκφραση 1 * 2 * 3 * 4 * 5, αντικαταστήστε το "*" με τα σημάδια δράσης και τοποθετήστε τις αγκύλες ως εξής. Για να πάρετε μια παράσταση της οποίας η τιμή είναι 100.

Εργασία 2. Απαιτείται η αποκρυπτογράφηση της εγγραφής της αριθμητικής ισότητας, στην οποία οι αριθμοί αντικαθίστανται από γράμματα και διαφορετικοί αριθμοί αντικαθίστανται από διαφορετικά γράμματα, τα ίδια - τα ίδια.

ΠΕΝΤΕ - ΤΡΙΑ = ΔΥΟΕίναι γνωστό ότι αντί για το γράμμα ΕΝΑπρέπει να αντικαταστήσετε τον αριθμό 2.

Εργασία 3. Πώς να χωρίσετε 80 κιλά καρφιά σε δύο μέρη - 15 κιλά και 65 κιλά χρησιμοποιώντας μια ζυγαριά χωρίς βάρη;

Εργασία 4. Κόψτε τη φιγούρα που φαίνεται στην εικόνα σε δύο ίσα μέρη έτσι ώστε να υπάρχει ένα αστέρι σε κάθε μέρος. Μπορείτε να κόψετε μόνο κατά μήκος των γραμμών του πλέγματος.

Εργασία 5. Ένα φλιτζάνι και ένα πιατάκι μαζί κοστίζουν 25 ρούβλια και 4 φλιτζάνια και 3 πιατάκια κοστίζουν 88 ρούβλια. Βρείτε την τιμή του φλιτζανιού και την τιμή του πιατιού.

6η τάξη.

Ασκηση 1. Συγκρίνετε κλάσματα χωρίς να τα φέρετε σε κοινό παρονομαστή.

Εργασία 2. Απαιτείται η αποκρυπτογράφηση της εγγραφής της αριθμητικής ισότητας, στην οποία οι αριθμοί αντικαθίστανται από γράμματα και διαφορετικοί αριθμοί αντικαθίστανται από διαφορετικά γράμματα, τα ίδια - τα ίδια. Υποτίθεται ότι η αρχική ισότητα είναι σωστή και γράφεται σύμφωνα με τους συνήθεις κανόνες της αριθμητικής.

ΔΟΥΛΕΙΑ
+ ΘΑ
ΤΥΧΗ

Εργασία 3. Τρεις φίλοι ήρθαν στην καλοκαιρινή κατασκήνωση για να ξεκουραστούν: ο Misha, ο Volodya και ο Petya. Είναι γνωστό ότι καθένας από αυτούς έχει ένα από τα ακόλουθα επώνυμα: Ivanov, Semenov, Gerasimov. Ο Misha δεν είναι ο Gerasimov. Ο πατέρας της Volodya είναι μηχανικός. Ο Volodya είναι μαθητής της 6ης τάξης. Ο Gerasimov είναι μαθητής της 5ης τάξης. Ο πατέρας του Ιβάνοφ είναι δάσκαλος. Ποιο είναι το επίθετο καθενός από τους τρεις φίλους;

Εργασία 4. Χωρίστε το σχήμα κατά μήκος των γραμμών του πλέγματος σε τέσσερα ίσα μέρη έτσι ώστε να υπάρχει ένα σημείο σε κάθε μέρος.

Εργασία 5. Η λιβελούλα που πηδούσε κοιμόταν τη μισή ώρα κάθε μέρας του κόκκινου καλοκαιριού, το ένα τρίτο της ώρας κάθε μέρας χόρευε και το ένα έκτο της ώρας τραγουδούσε. Τον υπόλοιπο χρόνο αποφάσισε να αφιερώσει στην προετοιμασία για το χειμώνα. Πόσες ώρες την ημέρα προετοιμαζόταν το Dragonfly για τον χειμώνα;

7η τάξη.

Ασκηση 1. Λύστε το rebus εάν είναι γνωστό ότι το μεγαλύτερο ψηφίο στον αριθμό STRENGTH είναι το 5:

ΑΠΟΦΑΣΙΖΩ
ΑΝ
Ισχυρός

Εργασία 2. Λύστε την εξίσωση│7 - x│ = 9,3

Εργασία 3. Μετά από επτά πλύσεις, το μήκος, το πλάτος και το πάχος του σαπουνιού μειώθηκαν στο μισό. Πόσες από τις ίδιες πλύσεις θα διαρκέσει το υπόλοιπο σαπούνι;

Εργασία 4 ... Διαχωρίστε ένα ορθογώνιο 4 × 9 κελιών κατά μήκος των πλευρών των κελιών σε δύο ίσα μέρη, ώστε στη συνέχεια να δημιουργήσετε ένα τετράγωνο από αυτά.

Εργασία 5. Ο ξύλινος κύβος βάφτηκε με λευκή μπογιά σε όλες τις πλευρές και στη συνέχεια κόπηκε σε 64 ίδιους κύβους. Πόσοι κύβοι είναι χρωματισμένοι στις τρεις πλευρές; Και στις δύο πλευρές?
Από τη μία πλευρά; Πόσοι κύβοι δεν είναι χρωματισμένοι;

8η τάξη.

Ασκηση 1. Σε ποια διψήφια τελειώνει ο αριθμός 13!

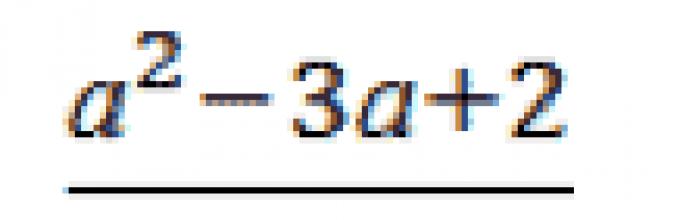
Εργασία 2. Μειώστε το κλάσμα:

Εργασία 3. Σχολική δραματική λέσχη, ετοιμάζεται για την ανάρτηση αποσπάσματος από τον Α.Σ. Ο Πούσκιν για τον Τσάρο Σαλτάν, αποφάσισε να διανείμει τους ρόλους μεταξύ των συμμετεχόντων.
- Θα είμαι Τσερνομόρ, - είπε ο Γιούρα.
- Όχι, θα είμαι Τσερνομόρ, - είπε ο Κόλια.
- Εντάξει, - του παραδέχτηκε η Γιούρα, - μπορώ να παίξω τον Guidon.
- Λοιπόν, μπορώ να γίνω Saltan, - ο Κόλια έδειξε επίσης συμμόρφωση.
- Συμφωνώ να είμαι μόνο ο Guidon! - είπε ο Μίσα.
Οι επιθυμίες των αγοριών ικανοποιήθηκαν. Πώς κατανεμήθηκαν οι ρόλοι;

Εργασία 4. Η διάμεσος ΑΔ σχεδιάζεται σε ισοσκελές τρίγωνο ΑΒΓ με βάση ΑΒ = 8m. Η περίμετρος του τριγώνου АСD είναι μεγαλύτερη από την περίμετρο του τριγώνου ABD κατά 2 m. Βρείτε AU.

Εργασία 5. Ο Νικολάι αγόρασε ένα γενικό σημειωματάριο 96 φύλλων και αριθμημένες σελίδες από το 1 έως το 192. Ο ανιψιός του Άρθουρ έσκισε 35 φύλλα από αυτό το σημειωματάριο και συγκέντρωσε και τους 70 αριθμούς που είναι γραμμένοι σε αυτά. Θα μπορούσε να ήταν το 2010.

Βαθμός 9.

Ασκηση 1. Βρείτε το τελευταίο ψηφίο του 1989 1989.

Εργασία 2. Το άθροισμα των ριζών κάποιας δευτεροβάθμιας εξίσωσης είναι ίσο με 1 και το άθροισμα των τετραγώνων τους ίσο με 2. Ποιο είναι το άθροισμα των κύβων τους;

Εργασία 3. Χρησιμοποιώντας τις τρεις διάμεσους m a, m b και m c ∆ ABC, βρείτε το μήκος της πλευράς AC = b.

Εργασία 4. Μειώστε το κλάσμα .

Εργασία 5. Με πόσους τρόπους μπορείτε να επιλέξετε τα φωνήεντα και τα σύμφωνα στη λέξη "καμισόλα";

Βαθμός 10.

Ασκηση 1. Επί του παρόντος, υπάρχουν νομίσματα των 1, 2, 5, 10 ρούβλια. Υποδείξτε όλα τα χρηματικά ποσά που μπορούν να πληρωθούν τόσο με ζυγό όσο και με μονό αριθμό νομισμάτων.

Εργασία 2. Αποδείξτε ότι το 5 + 5 2 + 5 3 +… + 5 2010 διαιρείται με το 6.

Εργασία 3. Σε ένα τετράγωνο Α Β Γ Δοι διαγώνιοι συναντώνται στο σημείο Μ... Είναι γνωστό ότι ΠΜ = 1,
VM = 2, CM = 4... Σε ποιες αξίες DMτετράπλευρο Α Β Γ Δείναι τραπεζοειδές;

Εργασία 4. Λύστε το σύστημα των εξισώσεων

Εργασία 5. Τριάντα μαθητές - δέκατη και ενδέκατη τάξη - έδωσαν τα χέρια. Αποδείχθηκε ότι κάθε μαθητής της δέκατης τάξης έσφιξε τα χέρια με οκτώ μαθητές της ενδέκατης τάξης και κάθε μαθητής της ενδέκατης τάξης έσφιξε τα χέρια με μαθητές της επτά δέκατης τάξης. Πόσοι ήταν οι μαθητές της δέκατης τάξης και πόσοι οι μαθητές της ενδέκατης τάξης;

Πρόβλημα 16:

Είναι δυνατόν να αλλάξετε 25 ρούβλια με δέκα λογαριασμούς 1, 3 και 5 ρούβλια; Λύση:

Απάντηση: Όχι

Η Petya αγόρασε ένα γενικό σημειωματάριο με όγκο 96 φύλλων και αρίθμησε όλες τις σελίδες του με τη σειρά με αριθμούς από το 1 έως το 192. Ο Βάσια έσκισε 25 φύλλα αυτού του σημειωματάριου και πρόσθεσε και τους 50 αριθμούς που είναι γραμμένοι σε αυτά. Θα μπορούσε να ήταν το 1990; Λύση:

Σε κάθε φύλλο, το άθροισμα των αριθμών σελίδων είναι περιττό και το άθροισμα 25 περιττών αριθμών είναι περιττό.

Το γινόμενο 22 ακεραίων είναι 1. Να αποδείξετε ότι το άθροισμά τους δεν είναι μηδέν. Λύση:

Μεταξύ αυτών των αριθμών υπάρχει ένας ζυγός αριθμός "μείον ένα", και για να είναι το άθροισμα ίσο με μηδέν, πρέπει να υπάρχουν ακριβώς 11 από αυτούς.

Είναι δυνατόν να φτιάξουμε ένα μαγικό τετράγωνο από τους πρώτους 36 πρώτους; Λύση:

Μεταξύ αυτών των αριθμών, ο ένας (2) είναι άρτιος και οι υπόλοιποι είναι περιττοί. Επομένως, στην ευθεία όπου είναι το δύο, το άθροισμα των αριθμών είναι περιττό και στις άλλες είναι άρτιος.

Οι αριθμοί από το 1 έως το 10 είναι γραμμένοι στη σειρά. Είναι δυνατόν να τοποθετηθούν τα σημάδια "+" και "-" μεταξύ τους έτσι ώστε η τιμή της παράστασης που προκύπτει να είναι ίση με μηδέν;

Σημείωση: Σημειώστε ότι οι αρνητικοί αριθμοί μπορεί επίσης να είναι άρτιοι και περιττοί. Λύση:

Πράγματι, το άθροισμα των αριθμών από το 1 έως το 10 είναι 55 και αλλάζοντας τα σημάδια σε αυτό, αλλάζουμε ολόκληρη την έκφραση σε ζυγό αριθμό.

Η ακρίδα πηδά σε ευθεία γραμμή και την πρώτη φορά πήδηξε 1 cm προς μία κατεύθυνση, τη δεύτερη φορά - 2 cm και ούτω καθεξής. Αποδείξτε ότι μετά τα άλματα του 1985 δεν μπορεί να επιστρέψει εκεί που ξεκίνησε. Λύση:

Σημείωση: Το άθροισμα 1 + 2 +… + 1985 είναι περιττό.

Στον πίνακα γράφονται οι αριθμοί 1, 2, 3,…, 1984, 1985. Επιτρέπεται η διαγραφή δύο αριθμών από τον πίνακα και η καταγραφή της απόλυτης τιμής της διαφοράς τους. Στο τέλος, ένας αριθμός θα παραμείνει στον πίνακα. Μπορεί να είναι μηδέν; Λύση:

Ελέγξτε ότι οι παραπάνω πράξεις δεν αλλάζουν την ισοτιμία του αθροίσματος όλων των αριθμών που είναι γραμμένοι στον πίνακα.

Είναι δυνατόν να καλύψουμε μια σκακιέρα με 1 × 2 ντόμινο έτσι ώστε μόνο τα κελιά a1 και h8 να παραμείνουν ελεύθερα; Λύση:

Κάθε ντόμινο καλύπτει ένα μαύρο και ένα άσπρο τετράγωνο και όταν αφαιρεθούν τα τετράγωνα a1 και h8, τα μαύρα τετράγωνα παραμένουν 2 λιγότερα από τα λευκά τετράγωνα.

Στον 17ψήφιο αριθμό προστέθηκε ο αριθμός που γράφτηκε με τα ίδια ψηφία, αλλά με αντίστροφη σειρά. Να αποδείξετε ότι τουλάχιστον ένα ψηφίο του ληφθέντος αθροίσματος είναι άρτιο. Λύση:

Εξετάστε δύο περιπτώσεις: το άθροισμα του πρώτου και του τελευταίου ψηφίου του αριθμού είναι μικρότερο από 10 και το άθροισμα του πρώτου και του τελευταίου ψηφίου του αριθμού δεν είναι μικρότερο από 10. Αν υποθέσουμε ότι όλα τα ψηφία του αθροίσματος είναι περιττά , τότε στην πρώτη περίπτωση δεν πρέπει να υπάρχει ένας ενιαίος παύλας στα ψηφία (που, προφανώς, οδηγεί σε αντίφαση), και στη δεύτερη περίπτωση, η παρουσία μεταφοράς κατά τη μετακίνηση από δεξιά προς τα αριστερά ή από τα αριστερά προς τα δεξιά εναλλάσσεται με η απουσία μεταφοράς, και ως αποτέλεσμα παίρνουμε ότι το αθροιστικό ψηφίο στο ένατο ψηφίο είναι αναγκαστικά άρτιο.

Στη λαϊκή ομάδα είναι 100 άτομα και κάθε απόγευμα τρεις από αυτούς πηγαίνουν σε υπηρεσία. Θα μπορούσε μετά από λίγο να αποδειχτεί ότι όλοι είχαν εφημερία ακριβώς μια φορά; Λύση:

Εφόσον σε κάθε ρολόι στο οποίο συμμετέχει αυτό το άτομο, εφημερεύει με άλλους δύο, τότε όλα τα υπόλοιπα μπορούν να χωριστούν σε ζευγάρια. Ωστόσο, το 99 είναι ένας περιττός αριθμός.

Υπάρχουν 45 σημεία στην ευθεία που βρίσκονται έξω από το τμήμα ΑΒ. Να αποδείξετε ότι το άθροισμα των αποστάσεων από αυτά τα σημεία στο σημείο Α δεν είναι ίσο με το άθροισμα των αποστάσεων από αυτά τα σημεία στο σημείο Β. Λύση:

Για οποιοδήποτε σημείο Χ που βρίσκεται έξω από το ΑΒ, έχουμε ΑΧ - ΒΧ = ± ΑΒ. Αν υποθέσουμε ότι τα αθροίσματα των αποστάσεων είναι ίσα, τότε παίρνουμε ότι η έκφραση ± AB ± AB ±… ± AB, στην οποία εμπλέκονται 45 όροι, είναι ίση με μηδέν. Αλλά αυτό είναι εξωπραγματικό.

Υπάρχουν 9 αριθμοί σε έναν κύκλο - 4 ένα και 5 μηδενικά. Κάθε δευτερόλεπτο, εκτελείται η ακόλουθη πράξη στους αριθμούς: το μηδέν τοποθετείται μεταξύ γειτονικών αριθμών εάν είναι διαφορετικοί και ένα εάν είναι ίσοι. μετά από αυτό διαγράφονται οι παλιοί αριθμοί. Μπορούν όλοι οι αριθμοί να γίνουν ίδιοι μετά από λίγο; Λύση:

Είναι σαφές ότι δεν μπορεί να επιτευχθεί συνδυασμός εννέα μονάδων νωρίτερα από εννέα μηδενικά. Αν υπήρχαν εννέα μηδενικά, τότε στην προηγούμενη κίνηση τα μηδενικά και τα ένα έπρεπε να εναλλάσσονται, κάτι που είναι αδύνατο, αφού υπάρχει μόνο ένας περιττός αριθμός.

25 αγόρια και 25 κορίτσια κάθονται σε ένα στρογγυλό τραπέζι. Αποδείξτε ότι ένας από αυτούς που κάθονται στο τραπέζι έχει και τα δύο αγόρια. Λύση:

Ας πραγματοποιήσουμε την απόδειξή μας με αντίφαση. Ας αριθμήσουμε όλους στο τραπέζι με τη σειρά, ξεκινώντας από κάποιο σημείο. Εάν ένα αγόρι κάθεται στην kη θέση, τότε είναι σαφές ότι τα κορίτσια κάθονται στις (k - 2) -η και (k + 2) -η θέση. Αλλά επειδή υπάρχουν ίσοι αριθμοί αγοριών και κοριτσιών, τότε για κάθε κορίτσι που κάθεται στην ντη θέση, είναι αλήθεια ότι τα αγόρια κάθονται στις (n - 2) και (n + 2) θέσεις. Αν τώρα λάβουμε υπόψη μόνο αυτά τα 25 άτομα που κάθονται σε «ζυγές» θέσεις, τότε παίρνουμε ότι μεταξύ αυτών αγόρια και κορίτσια εναλλάσσονται αν πάμε γύρω από το τραπέζι προς κάποια κατεύθυνση. Αλλά το 25 είναι μονός αριθμός.

Το σαλιγκάρι σέρνεται κατά μήκος του αεροπλάνου με σταθερή ταχύτητα, γυρνώντας σε ορθή γωνία κάθε 15 λεπτά. Αποδείξτε ότι μπορεί να επιστρέψει στο σημείο εκκίνησης μόνο μετά από έναν ακέραιο αριθμό ωρών. Λύση:

Είναι σαφές ότι ο αριθμός α των τμημάτων στα οποία το σαλιγκάρι σύρθηκε προς τα πάνω ή προς τα κάτω είναι ίσο με τον αριθμό των τμημάτων στα οποία σύρθηκε προς τα δεξιά ή προς τα αριστερά. Μένει μόνο να σημειωθεί ότι το α είναι άρτιο.

Τρεις ακρίδες παίζουν άλμα σε ευθεία γραμμή. Κάθε φορά ο ένας από αυτούς πηδάει πάνω από τον άλλον (αλλά όχι δύο ταυτόχρονα!). Θα μπορούσαν, μετά το άλμα του 1991, να βρίσκονται στα ίδια σημεία; Λύση:

Ας ονομάσουμε τις ακρίδες A, B και C. Καλέστε τις ακρίδες ABC, BCA και CAB (από αριστερά προς τα δεξιά) σωστές και ACB, BAC και CBA λανθασμένες. Είναι εύκολο να δει κανείς ότι το είδος της τοποθέτησης αλλάζει με οποιοδήποτε άλμα.

Υπάρχουν 101 νομίσματα, εκ των οποίων τα 50 είναι πλαστά, που διαφέρουν σε βάρος κατά 1 γραμμάριο από τα πραγματικά. Ο Petya πήρε ένα νόμισμα και σε ένα που ζυγίζει στη ζυγαριά με ένα βέλος που δείχνει τη διαφορά στα βάρη στα κύπελλα, θέλει να προσδιορίσει αν είναι ψεύτικο. Μπορεί να το κάνει; Λύση:

Πρέπει να αφήσετε αυτό το νόμισμα στην άκρη και, στη συνέχεια, να χωρίσετε τα υπόλοιπα 100 νομίσματα σε δύο στοίβες των 50 νομισμάτων το καθένα και να συγκρίνετε τα βάρη αυτών των στοίβων. Αν διαφέρουν κατά ζυγό αριθμό γραμμαρίων, τότε το νόμισμα που μας ενδιαφέρει είναι πραγματικό. Αν η διαφορά στα βάρη είναι περιττή, τότε το κέρμα είναι πλαστό.

Είναι δυνατόν να γράψετε αριθμούς από το 1 έως το 9 στη σειρά μία φορά, έτσι ώστε να υπάρχει ένας περιττός αριθμός ψηφίων μεταξύ ενός και δύο, δύο και τριών, ..., οκτώ και εννέα; Λύση:

Διαφορετικά, όλα τα ψηφία στη σειρά θα βρίσκονται σε σημεία της ίδιας ισοτιμίας.

Αυτό το έργο Petya αγόρασε ένα γενικό σημειωματάριο με όγκο 96 φύλλων και αρίθμησε όλες τις σελίδες του με τη σειρά με αριθμούς από το 1 έως το 192. Η Vasya έβγαλε (Έλεγχος) στο θέμα (AHD και οικονομική ανάλυση), ήταν προσαρμοσμένη από ειδικούς του η εταιρεία μας και πέρασε την επιτυχημένη υπεράσπισή του. Εργασία - Ο Petya αγόρασε ένα γενικό σημειωματάριο 96 φύλλων και αρίθμησε όλες τις σελίδες του με αριθμούς από το 1 έως το 192. Ο Vasya έβγαλε το θέμα του AHD και η οικονομική ανάλυση αντικατοπτρίζει το θέμα του και τη λογική συνιστώσα της αποκάλυψής του, την ουσία του θέμα υπό μελέτη αποκαλύπτεται, οι κύριες διατάξεις και οι κύριες ιδέες επισημαίνονται αυτό το θέμα.
Εργασία - Η Petya αγόρασε ένα γενικό σημειωματάριο με όγκο 96 φύλλων και αρίθμησε όλες τις σελίδες του με αριθμούς από το 1 έως το 192. Ο Vasya έβγαλε, περιέχει: πίνακες, σχέδια, τις πιο πρόσφατες λογοτεχνικές πηγές, το έτος παράδοσης και υπεράσπισης του εργασία - 2017. Στο έργο, η Petya αγόρασε έναν κοινό όγκο σημειωματάριων 96 φύλλων και αρίθμησε όλες τις σελίδες του με τη σειρά από το 1 έως το 192. Ο Vasya έβγαλε (AHD και οικονομική ανάλυση) αποκαλύπτεται η συνάφεια του ερευνητικού θέματος, ο βαθμός Η ανάπτυξη του προβλήματος αντικατοπτρίζεται, με βάση μια βαθιά αξιολόγηση και ανάλυση της επιστημονικής και μεθοδολογικής βιβλιογραφίας, σε εργασίες για το θέμα της AHD και της χρηματοοικονομικής ανάλυσης, το αντικείμενο της ανάλυσης και τα ζητήματά του εξετάζονται διεξοδικά, τόσο από θεωρητική όσο και από πρακτική πλευρά, διατυπώνονται ο στόχος και οι συγκεκριμένες εργασίες του θέματος που εξετάζουμε, υπάρχει η λογική της παρουσίασης του υλικού και η διαδοχή του.