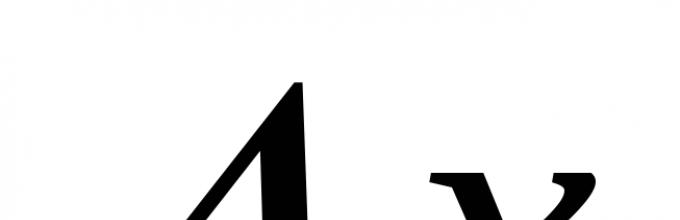Αφήνω Χ– όρισμα (ανεξάρτητη μεταβλητή). y=y(x)- λειτουργία.
Ας πάρουμε μια σταθερή τιμή ορίσματος x=x 0 και να υπολογίσετε την τιμή της συνάρτησης y 0 =y(x 0 ) . Τώρα ας ορίσουμε αυθαίρετα αύξηση (αλλαγή) του επιχειρήματος και να το δηλώσετε Χ ( Χμπορεί να είναι οποιουδήποτε σημείου).
Το όρισμα αύξησης είναι μια τελεία Χ 0 + Χ. Ας υποθέσουμε ότι περιέχει επίσης μια τιμή συνάρτησης y=y(x 0 + Χ)(βλέπε εικόνα).
Έτσι, με μια αυθαίρετη αλλαγή στην τιμή του ορίσματος, προκύπτει μια αλλαγή στη συνάρτηση, η οποία καλείται αύξηση τιμές συνάρτησης:
και δεν είναι αυθαίρετο, αλλά εξαρτάται από τον τύπο της συνάρτησης και την τιμή 
.
Αυξήσεις ορισμάτων και συναρτήσεων μπορεί να είναι τελικός, δηλ. εκφράζονται ως σταθεροί αριθμοί, οπότε μερικές φορές ονομάζονται πεπερασμένες διαφορές.
Στα οικονομικά, οι πεπερασμένες προσαυξήσεις θεωρούνται αρκετά συχνά. Για παράδειγμα, ο πίνακας δείχνει δεδομένα για το μήκος του σιδηροδρομικού δικτύου μιας συγκεκριμένης πολιτείας. Προφανώς, η αύξηση στο μήκος του δικτύου υπολογίζεται αφαιρώντας την προηγούμενη τιμή από την επόμενη.
Θα θεωρήσουμε το μήκος του σιδηροδρομικού δικτύου ως συνάρτηση, το επιχείρημα της οποίας θα είναι ο χρόνος (έτη).
|
Μήκος σιδηροδρόμου από τις 31 Δεκεμβρίου, χιλιάδες χιλιόμετρα. |
Αύξηση |
Μέση ετήσια ανάπτυξη |
|
Από μόνη της, μια αύξηση σε μια συνάρτηση (σε αυτή την περίπτωση, το μήκος του σιδηροδρομικού δικτύου) δεν χαρακτηρίζει καλά την αλλαγή στη λειτουργία. Στο παράδειγμά μας, από το γεγονός ότι 2,5>0,9 δεν μπορεί να συναχθεί το συμπέρασμα ότι το δίκτυο αναπτύχθηκε ταχύτερα 2000-2003 χρόνια παρά σε 2004 ζ., επειδή η προσαύξηση 2,5 αναφέρεται σε περίοδο τριών ετών και 0,9 - σε ένα μόνο χρόνο. Επομένως, είναι πολύ φυσικό μια αύξηση σε μια συνάρτηση να οδηγεί σε αλλαγή μονάδας στο όρισμα. Η αύξηση του επιχειρήματος εδώ είναι περίοδοι: 1996-1993=3; 2000-1996=4; 2003-2000=3; 2004-2003=1 .
Παίρνουμε αυτό που λέγεται στην οικονομική βιβλιογραφία μέση ετήσια ανάπτυξη.
Μπορείτε να αποφύγετε τη λειτουργία μείωσης της προσαύξησης στη μονάδα αλλαγής ορίσματος εάν λάβετε τις τιμές συνάρτησης για τιμές ορίσματος που διαφέρουν κατά μία, κάτι που δεν είναι πάντα δυνατό.
Στη μαθηματική ανάλυση, ιδιαίτερα στον διαφορικό λογισμό, λαμβάνονται υπόψη απειροελάχιστες (IM) αυξήσεις ορίσματος και συνάρτησης.
Διαφοροποίηση συνάρτησης μιας μεταβλητής (παράγωγος και διαφορικός) Παράγωγος συνάρτησης
Αυξήσεις ορίσματος και συνάρτησης σε ένα σημείο Χ 0 μπορούν να θεωρηθούν ως συγκρίσιμα απειροελάχιστα μεγέθη (βλ. θέμα 4, σύγκριση ΒΜ), δηλ. ΒΜ ίδιας τάξης.
Τότε ο λόγος τους θα έχει ένα πεπερασμένο όριο, το οποίο ορίζεται ως η παράγωγος της συνάρτησης στο t Χ 0 .
Όριο του λόγου της αύξησης μιας συνάρτησης προς την αύξηση BM του ορίσματος σε ένα σημείο x=x 0 που ονομάζεται παράγωγο λειτουργεί σε ένα δεδομένο σημείο.
Ο συμβολικός προσδιορισμός ενός παραγώγου με ένα εγκεφαλικό επεισόδιο (ή μάλλον, με τον ρωμαϊκό αριθμό I) εισήχθη από τον Newton. Μπορείτε επίσης να χρησιμοποιήσετε έναν δείκτη, ο οποίος δείχνει με ποια μεταβλητή υπολογίζεται η παράγωγος, για παράδειγμα, 
. Ένας άλλος συμβολισμός που προτάθηκε από τον ιδρυτή του λογισμού των παραγώγων, τον Γερμανό μαθηματικό Leibniz, χρησιμοποιείται επίσης ευρέως: 
. Θα μάθετε περισσότερα σχετικά με την προέλευση αυτού του χαρακτηρισμού στην ενότητα Διαφορικό συνάρτησης και διαφορικό ορίσματος.
Αυτός ο αριθμός υπολογίζεται Ταχύτητααλλαγές στη συνάρτηση που διέρχεται από ένα σημείο 
.
Ας εγκαταστήσουμε γεωμετρική σημασίαπαράγωγος συνάρτησης σε σημείο. Για το σκοπό αυτό, θα σχεδιάσουμε τη συνάρτηση y=y(x)και σημειώστε πάνω του τα σημεία που καθορίζουν την αλλαγή y(x)στο ενδιάμεσο 
Εφαπτομένη στη γραφική παράσταση μιας συνάρτησης σε ένα σημείο Μ 0
θα εξετάσουμε την οριακή θέση του τμήματος Μ 0
Μδεδομένου ότι 
(τελεία Μολισθαίνει κατά μήκος της γραφικής παράστασης μιας συνάρτησης σε ένα σημείο Μ 0
).
Ας σκεφτούμε 
. Προφανώς, 
.
Αν το σημείο Μκατευθύνουν κατά μήκος της γραφικής παράστασης της συνάρτησης προς το σημείο Μ 0
, μετά την τιμή 
θα τείνει σε ένα ορισμένο όριο, το οποίο συμβολίζουμε 
. Εν.
Οριακή γωνία
συμπίπτει με τη γωνία κλίσης της εφαπτομένης που σύρεται στη γραφική παράσταση της συνάρτησης συμπ. Μ 0
, άρα το παράγωγο 
αριθμητικά ίσο εφαπτομένη κλίση
στο καθορισμένο σημείο.
-
γεωμετρική σημασία της παραγώγου μιας συνάρτησης σε ένα σημείο.
Έτσι, μπορούμε να γράψουμε τις εφαπτομενικές και κανονικές εξισώσεις ( κανονικός - αυτή είναι μια ευθεία κάθετη στην εφαπτομένη) στη γραφική παράσταση της συνάρτησης σε κάποιο σημείο Χ 0 :
Εφαπτομένη - .
Κανονικό - 
.
Ενδιαφέρον παρουσιάζουν οι περιπτώσεις που αυτές οι γραμμές βρίσκονται οριζόντια ή κάθετα (βλ. Θέμα 3, ειδικές περιπτώσεις θέσης γραμμής σε επίπεδο). Επειτα,
Αν 
;
Αν 
.
Ο ορισμός της παραγώγου λέγεται ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση λειτουργίες.
Αν η συνάρτηση στο σημείο Χ 0 έχει πεπερασμένη παράγωγο, τότε λέγεται διαφοροποιήσιμοσε αυτό το σημείο. Μια συνάρτηση που είναι διαφορίσιμη σε όλα τα σημεία ενός συγκεκριμένου διαστήματος ονομάζεται διαφοροποιήσιμη σε αυτό το διάστημα.
Θεώρημα . Εάν η συνάρτηση y=y(x)διαφοροποιήσιμο συμπ. Χ 0 , τότε είναι συνεχής σε αυτό το σημείο.
Ετσι, συνέχεια– απαραίτητη (αλλά όχι επαρκής) προϋπόθεση για τη διαφοροποίηση μιας συνάρτησης.
Ορισμός 1
Εάν για κάθε ζεύγος $(x,y)$ τιμών δύο ανεξάρτητων μεταβλητών από κάποιο τομέα συσχετίζεται μια συγκεκριμένη τιμή $z$, τότε το $z$ λέγεται ότι είναι συνάρτηση δύο μεταβλητών $(x,y) $. Σημείωση: $z=f(x,y)$.
Σε σχέση με τη συνάρτηση $z=f(x,y)$, ας εξετάσουμε τις έννοιες γενικών (συνολικών) και μερικών προσαυξήσεων μιας συνάρτησης.
Έστω μια συνάρτηση $z=f(x,y)$ δύο ανεξάρτητων μεταβλητών $(x,y)$.
Σημείωση 1
Εφόσον οι μεταβλητές $(x,y)$ είναι ανεξάρτητες, η μία από αυτές μπορεί να αλλάξει, ενώ η άλλη παραμένει σταθερή.
Ας δώσουμε στη μεταβλητή $x$ μια αύξηση $\Delta x$, διατηρώντας την τιμή της μεταβλητής $y$ αμετάβλητη.
Τότε η συνάρτηση $z=f(x,y)$ θα λάβει μια αύξηση, η οποία θα ονομάζεται μερική αύξηση της συνάρτησης $z=f(x,y)$ σε σχέση με τη μεταβλητή $x$. Ονομασία:
Ομοίως, θα δώσουμε στη μεταβλητή $y$ μια αύξηση $\Delta y$, διατηρώντας την τιμή της μεταβλητής $x$ αμετάβλητη.
Τότε η συνάρτηση $z=f(x,y)$ θα λάβει μια αύξηση, η οποία θα ονομάζεται μερική αύξηση της συνάρτησης $z=f(x,y)$ σε σχέση με τη μεταβλητή $y$. Ονομασία:
Εάν στο όρισμα $x$ δοθεί μια αύξηση $\Delta x$ και στο όρισμα $y$ προσαυξηθεί $\Delta y$, τότε προκύπτει η συνολική αύξηση δεδομένη λειτουργία$z=f(x,y)$. Ονομασία:
Έτσι έχουμε:
$\Delta _(x) z=f(x+\Delta x,y)-f(x,y)$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ πάνω από $x$;
$\Delta _(y) z=f(x,y+\Delta y)-f(x,y)$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ κατά $y$;
$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$ - συνολική αύξηση της συνάρτησης $z=f(x,y)$.
Παράδειγμα 1
Λύση:
$\Delta _(x) z=x+\Delta x+y$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ κατά $x$;
$\Delta _(y) z=x+y+\Delta y$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ σε σχέση με το $y$.
$\Delta z=x+\Delta x+y+\Delta y$ - συνολική αύξηση της συνάρτησης $z=f(x,y)$.
Παράδειγμα 2
Υπολογίστε τη μερική και ολική αύξηση της συνάρτησης $z=xy$ στο σημείο $(1;2)$ για $\Delta x=0,1;\, \, \Delta y=0,1$.
Λύση:
Με τον ορισμό της μερικής αύξησης βρίσκουμε:
$\Delta _(x) z=(x+\Delta x)\cdot y$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ πάνω από $x$
$\Delta _(y) z=x\cdot (y+\Delta y)$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ κατά $y$;
Με τον ορισμό της συνολικής αύξησης βρίσκουμε:
$\Delta z=(x+\Delta x)\cdot (y+\Delta y)$ - συνολική αύξηση της συνάρτησης $z=f(x,y)$.
Ως εκ τούτου,
\[\Δέλτα _(x) z=(1+0,1)\cdot 2=2,2\] \[\Δέλτα _(y) z=1\cdot (2+0,1)=2,1 \] \[\Δέλτα z= (1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]
Σημείωση 2
Η συνολική αύξηση μιας δεδομένης συνάρτησης $z=f(x,y)$ δεν είναι ίση με το άθροισμα των μερικών της αυξήσεων $\Delta _(x) z$ και $\Delta _(y) z$. Μαθηματικός συμβολισμός: $\Delta z\ne \Delta _(x) z+\Delta _(y) z$.
Παράδειγμα 3
Ελέγξτε τις παρατηρήσεις ισχυρισμών για λειτουργία
Λύση:
$\Delta _(x) z=x+\Delta x+y$; $\Delta _(y) z=x+y+\Delta y$; $\Delta z=x+\Delta x+y+\Delta y$ (που λαμβάνεται στο παράδειγμα 1)
Ας βρούμε το άθροισμα των μερικών αυξήσεων μιας δεδομένης συνάρτησης $z=f(x,y)$
\[\Delta _(x) z+\Delta _(y) z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]
\[\Delta _(x) z+\Delta _(y) z\ne \Delta z.\]
Ορισμός 2
Εάν για κάθε τριπλό $(x,y,z)$ τιμών τριών ανεξάρτητων μεταβλητών από κάποιο τομέα συσχετίζεται μια συγκεκριμένη τιμή $w$, τότε το $w$ λέγεται ότι είναι συνάρτηση τριών μεταβλητών $(x, y,z)$ σε αυτήν την περιοχή.
Σημείωση: $w=f(x,y,z)$.
Ορισμός 3
Εάν για κάθε σύνολο $(x,y,z,...,t)$ τιμών ανεξάρτητων μεταβλητών από μια συγκεκριμένη περιοχή συσχετίζεται μια συγκεκριμένη τιμή $w$, τότε το $w$ λέγεται ότι είναι συνάρτηση του οι μεταβλητές $(x,y, z,...,t)$ σε αυτήν την περιοχή.
Σημείωση: $w=f(x,y,z,...,t)$.
Για μια συνάρτηση τριών ή περισσότερων μεταβλητών, με τον ίδιο τρόπο όπως για μια συνάρτηση δύο μεταβλητών, προσδιορίζονται μερικές προσαυξήσεις για καθεμία από τις μεταβλητές:
$\Delta _(z) w=f(x,y,z+\Delta z)-f(x,y,z)$ - μερική αύξηση της συνάρτησης $w=f(x,y,z,... ,t )$ κατά $z$;
$\Delta _(t) w=f(x,y,z,...,t+\Delta t)-f(x,y,z,...,t)$ - μερική αύξηση της συνάρτησης $w =f (x,y,z,...,t)$ επί $t$.
Παράδειγμα 4
Γράψτε συναρτήσεις μερικής και ολικής αύξησης
Λύση:
Με τον ορισμό της μερικής αύξησης βρίσκουμε:
$\Delta _(x) w=((x+\Delta x)+y)\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $x$
$\Delta _(y) w=(x+(y+\Delta y))\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $y$;
$\Delta _(z) w=(x+y)\cdot (z+\Delta z)$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $z$;
Με τον ορισμό της συνολικής αύξησης βρίσκουμε:
$\Delta w=((x+\Delta x)+(y+\Delta y))\cdot (z+\Delta z)$ - συνολική αύξηση της συνάρτησης $w=f(x,y,z)$.
Παράδειγμα 5
Υπολογίστε τη μερική και ολική αύξηση της συνάρτησης $w=xyz$ στο σημείο $(1;2;1)$ για $\Delta x=0,1;\, \, \Delta y=0,1;\, \, \Δέλτα z=0,1$.
Λύση:
Με τον ορισμό της μερικής αύξησης βρίσκουμε:
$\Delta _(x) w=(x+\Delta x)\cdot y\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $x$
$\Delta _(y) w=x\cdot (y+\Delta y)\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ κατά $y$;
$\Delta _(z) w=x\cdot y\cdot (z+\Delta z)$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $z$;
Με τον ορισμό της συνολικής αύξησης βρίσκουμε:
$\Delta w=(x+\Delta x)\cdot (y+\Delta y)\cdot (z+\Delta z)$ - συνολική αύξηση της συνάρτησης $w=f(x,y,z)$.
Ως εκ τούτου,
\[\Δέλτα _(x) w=(1+0,1)\cdot 2\cdot 1=2,2\] \[\Delta _(y) w=1\cdot (2+0,1)\ cdot 1=2,1\] \[\Δέλτα _(y) w=1\cdot 2\cdot (1+0,1)=2,2\] \[\Delta z=(1+0,1) \cdot (2+0,1)\cdot (1+0,1) =1,1\cdot 2,1\cdot 1,1=2,541.\]
ΜΕ γεωμετρικό σημείοΑπό άποψη προβολής, η συνολική αύξηση της συνάρτησης $z=f(x,y)$ (εξ ορισμού $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$) ισούται με την αύξηση της εφαρμογής της γραφικής παράστασης της συνάρτησης $z =f(x,y)$ όταν μετακινείται από το σημείο $M(x,y)$ στο σημείο $M_(1) (x+\Delta x,y+ \Δέλτα y)$ (Εικ. 1).
Εικόνα 1.
Έστω x ένα αυθαίρετο σημείο σε κάποια γειτονιά ενός σταθερού σημείου x 0 . η διαφορά x – x 0 ονομάζεται συνήθως προσαύξηση της ανεξάρτητης μεταβλητής (ή προσαύξηση ορίσματος) στο σημείο x 0 και συμβολίζεται Δx. Ετσι,
Δx = x –x 0 ,
απ' όπου προκύπτει ότι
Αύξηση συνάρτησης –τη διαφορά μεταξύ δύο τιμών συνάρτησης.
Αφήστε τη συνάρτηση να δοθεί στο = f(x), που ορίζεται με την τιμή του ορίσματος ίση με Χ 0 . Ας δώσουμε στο επιχείρημα μια αύξηση D Χ, ᴛ.ᴇ. θεωρήστε την τιμή του επιχειρήματος ίση με Χ 0+D Χ. Ας υποθέσουμε ότι αυτή η τιμή ορίσματος είναι επίσης εντός του πεδίου εφαρμογής αυτής της συνάρτησης. Τότε η διαφορά Δ y = f(x 0+D Χ) – f(x 0)Συνήθως ονομάζεται αύξηση μιας συνάρτησης. Αύξηση συνάρτησης φά(Χ) στο σημείο Χ- συνάρτηση που συνήθως συμβολίζεται Δ x σταπό τη νέα μεταβλητή Δ Χοριζεται ως
Δ x στ(Δ Χ) = φά(Χ + Δ Χ) − φά(Χ).
Να βρείτε την αύξηση του ορίσματος και την αύξηση της συνάρτησης στο σημείο x 0 αν
Παράδειγμα 2. Να βρείτε την αύξηση της συνάρτησης f(x) = x 2 αν x = 1, ∆x = 0,1
Λύση: f(x) = x 2, f(x+∆x) = (x+∆x) 2
Ας βρούμε την αύξηση της συνάρτησης ∆f = f(x+∆x) - f(x) = (x+∆x) 2 - x 2 = x 2 +2x*∆x+∆x 2 - x 2 = 2x*∆x + ∆x 2 /
Αντικαταστήστε τις τιμές x=1 και ∆x= 0,1, παίρνουμε Δf = 2*1*0,1 + (0,1) 2 = 0,2+0,01 = 0,21
Βρείτε την αύξηση του ορίσματος και την αύξηση της συνάρτησης στο σημείο x 0
2.f(x) = 2x 3. x 0 =3 x=2,4
3. f(x) = 2x 2 +2 x 0 =1 x=0,8
4. f(x) = 3x+4 x 0 =4 x=3,8
Ορισμός: Παράγωγομιας συνάρτησης σε ένα σημείο, συνηθίζεται να καλούμε το όριο (αν υπάρχει και είναι πεπερασμένο) του λόγου της αύξησης της συνάρτησης προς την αύξηση του ορίσματος, με την προϋπόθεση ότι το τελευταίο τείνει στο μηδέν.
Οι πιο συχνά χρησιμοποιούμενοι συμβολισμοί παραγώγων είναι:
Ετσι,
Η εύρεση της παραγώγου συνήθως ονομάζεται ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση . Εισήχθη ορισμός μιας διαφοροποιήσιμης συνάρτησης: Μια συνάρτηση f που έχει μια παράγωγο σε κάθε σημείο ενός συγκεκριμένου διαστήματος συνήθως ονομάζεται διαφοροποιήσιμη σε αυτό το διάστημα.
Έστω μια συνάρτηση που ορίζεται σε μια συγκεκριμένη γειτονιά ενός σημείου.Η παράγωγος μιας συνάρτησης συνήθως ονομάζεται αριθμός έτσι ώστε η συνάρτηση στη γειτονιά U(Χ 0) μπορεί να αναπαρασταθεί ως
φά(Χ 0 + η) = φά(Χ 0) + Αχ + ο(η)
αν υπάρχει.
Προσδιορισμός της παραγώγου μιας συνάρτησης σε ένα σημείο.
Αφήστε τη λειτουργία f(x)που ορίζεται στο διάστημα (α; β), και είναι τα σημεία αυτού του διαστήματος.
Ορισμός. Παράγωγος συνάρτησης f(x)σε ένα σημείο συνηθίζεται να ονομάζουμε το όριο του λόγου της αύξησης μιας συνάρτησης προς την αύξηση του ορίσματος στο . Συμβολίζεται με .
Όταν το τελευταίο όριο παίρνει μια συγκεκριμένη τελική τιμή, μιλάμε για ύπαρξη πεπερασμένη παράγωγος στο σημείο. Αν το όριο είναι άπειρο, τότε το λέμε η παράγωγος είναι άπειρη σε ένα δεδομένο σημείο. Αν το όριο δεν υπάρχει, τότε η παράγωγος της συνάρτησης σε αυτό το σημείο δεν υπάρχει.
Λειτουργία f(x)λέγεται ότι είναι διαφορίσιμο σε ένα σημείο που έχει μια πεπερασμένη παράγωγο σε αυτό.
Σε περίπτωση που η συνάρτηση f(x)διαφοροποιήσιμο σε κάθε σημείο κάποιου διαστήματος (α; β), τότε η συνάρτηση ονομάζεται διαφοροποιήσιμη σε αυτό το διάστημα. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, οποιοδήποτε σημείο Χαπό το ενδιάμεσο (α; β)μπορούμε να ταιριάξουμε την τιμή της παραγώγου της συνάρτησης σε αυτό το σημείο, δηλαδή έχουμε την ευκαιρία να ορίσουμε μια νέα συνάρτηση, η οποία ονομάζεται παράγωγος της συνάρτησης f(x)στο διάστημα (α; β).
Η λειτουργία εύρεσης της παραγώγου συνήθως ονομάζεται διαφοροποίηση.
Στη ζωή δεν μας ενδιαφέρουν πάντα οι ακριβείς τιμές οποιωνδήποτε ποσοτήτων. Μερικές φορές είναι ενδιαφέρον να γνωρίζουμε την αλλαγή αυτής της ποσότητας, για παράδειγμα, τη μέση ταχύτητα του λεωφορείου, την αναλογία της ποσότητας κίνησης προς τη χρονική περίοδο κ.λπ. Για να συγκρίνετε την τιμή μιας συνάρτησης σε ένα συγκεκριμένο σημείο με τις τιμές της ίδιας συνάρτησης σε άλλα σημεία, είναι βολικό να χρησιμοποιήσετε έννοιες όπως "αύξηση συνάρτησης" και "αύξηση ορίσματος".
Οι έννοιες της «αύξησης συνάρτησης» και της «αύξησης επιχειρήματος»
Ας πούμε ότι το x είναι κάποιο αυθαίρετο σημείο που βρίσκεται σε κάποια γειτονιά του σημείου x0. Η αύξηση του ορίσματος στο σημείο x0 είναι η διαφορά x-x0. Η προσαύξηση ορίζεται ως εξής: ∆x.
- ∆x=x-x0.
Μερικές φορές αυτή η ποσότητα ονομάζεται επίσης αύξηση της ανεξάρτητης μεταβλητής στο σημείο x0. Από τον τύπο προκύπτει: x = x0+∆x. Σε τέτοιες περιπτώσεις, λένε ότι η αρχική τιμή της ανεξάρτητης μεταβλητής x0 έλαβε μια αύξηση Δx.
Αν αλλάξουμε το όρισμα, τότε θα αλλάξει και η τιμή της συνάρτησης.
- f(x) - f(x0) = f(x0 + ∆х) - f(x0).
Αύξηση της συνάρτησης f στο σημείο x0,η αντίστοιχη αύξηση ∆х είναι η διαφορά f(x0 + ∆х) - f(x0). Η αύξηση μιας συνάρτησης συμβολίζεται ως εξής: ∆f. Έτσι παίρνουμε εξ ορισμού:
- ∆f= f(x0 +∆x) - f(x0).
Μερικές φορές, η ∆f ονομάζεται επίσης η αύξηση της εξαρτημένης μεταβλητής και η Δу χρησιμοποιείται για αυτόν τον προσδιορισμό εάν η συνάρτηση ήταν, για παράδειγμα, y=f(x).
Γεωμετρική έννοια της προσαύξησης
Κοιτάξτε την παρακάτω εικόνα.
Όπως μπορείτε να δείτε, η προσαύξηση δείχνει την αλλαγή της τεταγμένης και της τετμημένης ενός σημείου. Και ο λόγος της αύξησης της συνάρτησης προς την αύξηση του ορίσματος καθορίζει τη γωνία κλίσης της τομής που διέρχεται από την αρχική και την τελική θέση του σημείου.
Ας δούμε παραδείγματα αύξησης συνάρτησης και ορίσματος
Παράδειγμα 1.Να βρείτε την αύξηση του ορίσματος ∆x και την αύξηση της συνάρτησης ∆f στο σημείο x0, αν f(x) = x 2, x0=2 α) x=1,9 β) x =2,1
Ας χρησιμοποιήσουμε τους τύπους που δίνονται παραπάνω:
α) ∆х=х-х0 = 1,9 - 2 = -0,1;
- ∆f=f(1,9) - f(2) = 1,9 2 - 2 2 = -0,39;
β) ∆x=x-x0=2,1-2=0,1;
- ∆f=f(2,1) - f(2) = 2,1 2 - 2 2 = 0,41.
Παράδειγμα 2.Υπολογίστε την αύξηση ∆f για τη συνάρτηση f(x) = 1/x στο σημείο x0 αν η αύξηση του ορίσματος είναι ίση με Δx.
Και πάλι, θα χρησιμοποιήσουμε τους τύπους που ελήφθησαν παραπάνω.
- ∆f = f(x0 + ∆x) - f(x0) =1/(x0-∆x) - 1/x0 = (x0 - (x0+∆x))/(x0*(x0+∆x)) = - ∆x/((x0*(x0+∆x)).
Ορισμός 1
Εάν για κάθε ζεύγος $(x,y)$ τιμών δύο ανεξάρτητων μεταβλητών από κάποιο τομέα συσχετίζεται μια συγκεκριμένη τιμή $z$, τότε το $z$ λέγεται ότι είναι συνάρτηση δύο μεταβλητών $(x,y) $. Σημείωση: $z=f(x,y)$.
Σε σχέση με τη συνάρτηση $z=f(x,y)$, ας εξετάσουμε τις έννοιες γενικών (συνολικών) και μερικών προσαυξήσεων μιας συνάρτησης.
Έστω μια συνάρτηση $z=f(x,y)$ δύο ανεξάρτητων μεταβλητών $(x,y)$.
Σημείωση 1
Εφόσον οι μεταβλητές $(x,y)$ είναι ανεξάρτητες, η μία από αυτές μπορεί να αλλάξει, ενώ η άλλη παραμένει σταθερή.
Ας δώσουμε στη μεταβλητή $x$ μια αύξηση $\Delta x$, διατηρώντας την τιμή της μεταβλητής $y$ αμετάβλητη.
Τότε η συνάρτηση $z=f(x,y)$ θα λάβει μια αύξηση, η οποία θα ονομάζεται μερική αύξηση της συνάρτησης $z=f(x,y)$ σε σχέση με τη μεταβλητή $x$. Ονομασία:
Ομοίως, θα δώσουμε στη μεταβλητή $y$ μια αύξηση $\Delta y$, διατηρώντας την τιμή της μεταβλητής $x$ αμετάβλητη.
Τότε η συνάρτηση $z=f(x,y)$ θα λάβει μια αύξηση, η οποία θα ονομάζεται μερική αύξηση της συνάρτησης $z=f(x,y)$ σε σχέση με τη μεταβλητή $y$. Ονομασία:
Εάν στο όρισμα $x$ δοθεί μια αύξηση $\Delta x$ και στο όρισμα $y$ δοθεί μια αύξηση $\Delta y$, τότε η πλήρης αύξηση της δεδομένης συνάρτησης $z=f(x,y)$ λαμβάνεται. Ονομασία:
Έτσι έχουμε:
$\Delta _(x) z=f(x+\Delta x,y)-f(x,y)$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ πάνω από $x$;
$\Delta _(y) z=f(x,y+\Delta y)-f(x,y)$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ κατά $y$;
$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$ - συνολική αύξηση της συνάρτησης $z=f(x,y)$.
Παράδειγμα 1
Λύση:
$\Delta _(x) z=x+\Delta x+y$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ κατά $x$;
$\Delta _(y) z=x+y+\Delta y$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ σε σχέση με το $y$.
$\Delta z=x+\Delta x+y+\Delta y$ - συνολική αύξηση της συνάρτησης $z=f(x,y)$.
Παράδειγμα 2
Υπολογίστε τη μερική και ολική αύξηση της συνάρτησης $z=xy$ στο σημείο $(1;2)$ για $\Delta x=0,1;\, \, \Delta y=0,1$.
Λύση:
Με τον ορισμό της μερικής αύξησης βρίσκουμε:
$\Delta _(x) z=(x+\Delta x)\cdot y$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ πάνω από $x$
$\Delta _(y) z=x\cdot (y+\Delta y)$ - μερική αύξηση της συνάρτησης $z=f(x,y)$ κατά $y$;
Με τον ορισμό της συνολικής αύξησης βρίσκουμε:
$\Delta z=(x+\Delta x)\cdot (y+\Delta y)$ - συνολική αύξηση της συνάρτησης $z=f(x,y)$.
Ως εκ τούτου,
\[\Δέλτα _(x) z=(1+0,1)\cdot 2=2,2\] \[\Δέλτα _(y) z=1\cdot (2+0,1)=2,1 \] \[\Δέλτα z= (1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]
Σημείωση 2
Η συνολική αύξηση μιας δεδομένης συνάρτησης $z=f(x,y)$ δεν είναι ίση με το άθροισμα των μερικών της αυξήσεων $\Delta _(x) z$ και $\Delta _(y) z$. Μαθηματικός συμβολισμός: $\Delta z\ne \Delta _(x) z+\Delta _(y) z$.
Παράδειγμα 3
Ελέγξτε τις παρατηρήσεις ισχυρισμών για λειτουργία
Λύση:
$\Delta _(x) z=x+\Delta x+y$; $\Delta _(y) z=x+y+\Delta y$; $\Delta z=x+\Delta x+y+\Delta y$ (που λαμβάνεται στο παράδειγμα 1)
Ας βρούμε το άθροισμα των μερικών αυξήσεων μιας δεδομένης συνάρτησης $z=f(x,y)$
\[\Delta _(x) z+\Delta _(y) z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]
\[\Delta _(x) z+\Delta _(y) z\ne \Delta z.\]
Ορισμός 2
Εάν για κάθε τριπλό $(x,y,z)$ τιμών τριών ανεξάρτητων μεταβλητών από κάποιο τομέα συσχετίζεται μια συγκεκριμένη τιμή $w$, τότε το $w$ λέγεται ότι είναι συνάρτηση τριών μεταβλητών $(x, y,z)$ σε αυτήν την περιοχή.
Σημείωση: $w=f(x,y,z)$.
Ορισμός 3
Εάν για κάθε σύνολο $(x,y,z,...,t)$ τιμών ανεξάρτητων μεταβλητών από μια συγκεκριμένη περιοχή συσχετίζεται μια συγκεκριμένη τιμή $w$, τότε το $w$ λέγεται ότι είναι συνάρτηση του οι μεταβλητές $(x,y, z,...,t)$ σε αυτήν την περιοχή.
Σημείωση: $w=f(x,y,z,...,t)$.
Για μια συνάρτηση τριών ή περισσότερων μεταβλητών, με τον ίδιο τρόπο όπως για μια συνάρτηση δύο μεταβλητών, προσδιορίζονται μερικές προσαυξήσεις για καθεμία από τις μεταβλητές:
$\Delta _(z) w=f(x,y,z+\Delta z)-f(x,y,z)$ - μερική αύξηση της συνάρτησης $w=f(x,y,z,... ,t )$ κατά $z$;
$\Delta _(t) w=f(x,y,z,...,t+\Delta t)-f(x,y,z,...,t)$ - μερική αύξηση της συνάρτησης $w =f (x,y,z,...,t)$ επί $t$.
Παράδειγμα 4
Γράψτε συναρτήσεις μερικής και ολικής αύξησης
Λύση:
Με τον ορισμό της μερικής αύξησης βρίσκουμε:
$\Delta _(x) w=((x+\Delta x)+y)\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $x$
$\Delta _(y) w=(x+(y+\Delta y))\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $y$;
$\Delta _(z) w=(x+y)\cdot (z+\Delta z)$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $z$;
Με τον ορισμό της συνολικής αύξησης βρίσκουμε:
$\Delta w=((x+\Delta x)+(y+\Delta y))\cdot (z+\Delta z)$ - συνολική αύξηση της συνάρτησης $w=f(x,y,z)$.
Παράδειγμα 5
Υπολογίστε τη μερική και ολική αύξηση της συνάρτησης $w=xyz$ στο σημείο $(1;2;1)$ για $\Delta x=0,1;\, \, \Delta y=0,1;\, \, \Δέλτα z=0,1$.
Λύση:
Με τον ορισμό της μερικής αύξησης βρίσκουμε:
$\Delta _(x) w=(x+\Delta x)\cdot y\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $x$
$\Delta _(y) w=x\cdot (y+\Delta y)\cdot z$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ κατά $y$;
$\Delta _(z) w=x\cdot y\cdot (z+\Delta z)$ - μερική αύξηση της συνάρτησης $w=f(x,y,z)$ πάνω από $z$;
Με τον ορισμό της συνολικής αύξησης βρίσκουμε:
$\Delta w=(x+\Delta x)\cdot (y+\Delta y)\cdot (z+\Delta z)$ - συνολική αύξηση της συνάρτησης $w=f(x,y,z)$.
Ως εκ τούτου,
\[\Δέλτα _(x) w=(1+0,1)\cdot 2\cdot 1=2,2\] \[\Delta _(y) w=1\cdot (2+0,1)\ cdot 1=2,1\] \[\Δέλτα _(y) w=1\cdot 2\cdot (1+0,1)=2,2\] \[\Delta z=(1+0,1) \cdot (2+0,1)\cdot (1+0,1) =1,1\cdot 2,1\cdot 1,1=2,541.\]
Από γεωμετρική άποψη, η συνολική αύξηση της συνάρτησης $z=f(x,y)$ (εξ ορισμού $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y) $) ισούται με την αύξηση της εφαρμογής της συνάρτησης γραφήματος $z=f(x,y)$ όταν μετακινείται από το σημείο $M(x,y)$ στο σημείο $M_(1) (x+\Delta x,y+ \Δέλτα y)$ (Εικ. 1).
Εικόνα 1.
