1. Τα δύο πρώτα σημάδια ισότητας ορθογωνίων τριγώνων.
Για να είναι ίσα δύο τρίγωνα, αρκεί τρία στοιχεία του ενός τριγώνου να είναι ίσα με τα αντίστοιχα στοιχεία του άλλου τριγώνου και τα στοιχεία αυτά πρέπει οπωσδήποτε να περιλαμβάνουν τουλάχιστον τη μία πλευρά.
Δεδομένου ότι όλες οι ορθές γωνίες είναι ίσες μεταξύ τους, τα ορθογώνια τρίγωνα έχουν ήδη ένα ίσο στοιχείο, δηλαδή μια ορθή γωνία.

Από αυτό προκύπτει ότι τα ορθογώνια τρίγωνα είναι ίσα:
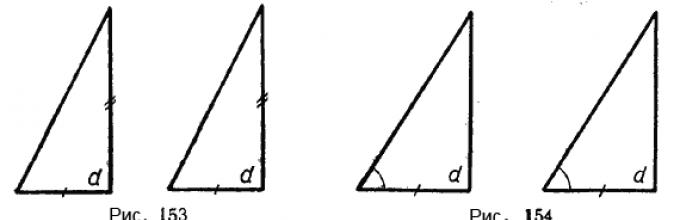
αν τα σκέλη ενός τριγώνου είναι αντίστοιχα ίσα με τα σκέλη ενός άλλου τριγώνου (Εικ. 153);
αν το σκέλος και η παρακείμενη οξεία γωνία ενός τριγώνου είναι αντίστοιχα ίσα με το σκέλος και την παρακείμενη οξεία γωνία του άλλου τριγώνου (Εικ. 154).
Ας αποδείξουμε τώρα δύο θεωρήματα που θεσπίζουν δύο ακόμη κριτήρια για την ισότητα των ορθογωνίων τριγώνων.
Θεωρήματα σε τεστ ισότητας ορθογωνίων τριγώνων
Θεώρημα 1. Αν η υποτείνουσα και η οξεία γωνία ενός τριγώνου είναι αντίστοιχα ίσες με την υποτείνουσα και την οξεία γωνία ενός άλλου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα.Για να αποδείξουμε αυτό το θεώρημα, ας κατασκευάσουμε δύο ορθογώνιες γωνίες ΑΒΓ και Α'Β'Γ', στις οποίες οι γωνίες Α και Α' είναι ίσες, οι υποτείνουσες ΑΒ και Α'Β' επίσης ίσες και οι γωνίες Γ και Γ'. έχουν δίκιο (Εικ. 157) .

Ας υπερθέσουμε το τρίγωνο A’B’C’ στο τρίγωνο ABC έτσι ώστε η κορυφή A’ να συμπίπτει με την κορυφή A, η υποτείνουσα A’B’ να συμπίπτει με την ίση υποτείνουσα AB. Στη συνέχεια, λόγω της ισότητας των γωνιών Α και Α', η πλευρά A'C' θα πάει κατά μήκος της πλευράς AC. Το σκέλος B’C’ θα συμπίπτει με το πόδι BC: και τα δύο είναι κάθετοι που σύρονται σε μια ευθεία γραμμή AC από ένα σημείο B. Αυτό σημαίνει ότι οι κορυφές C και C’ θα συμπίπτουν.
Το τρίγωνο ABC συμπίπτει με το τρίγωνο A'B'C'.
Επομένως, \(\Delta\)ABC = \(\Delta\)A'B'C'.
Το θεώρημα αυτό δίνει το 3ο κριτήριο για την ισότητα των ορθογωνίων τριγώνων (με την υποτείνουσα και την οξεία γωνία).
Θεώρημα 2. Αν η υποτείνουσα και το σκέλος ενός τριγώνου είναι αντίστοιχα ίσα με την υποτείνουσα και το σκέλος ενός άλλου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα.
Για να το αποδείξουμε αυτό, ας κατασκευάσουμε δύο ορθογώνια τρίγωνο ABCκαι A'B'C', όπου οι γωνίες C και C' είναι ορθές, τα σκέλη AC και A'C' ίσα, οι υποτείνουσες ΑΒ και A'B' είναι επίσης ίσες (Εικ. 158).

Ας σχεδιάσουμε μια ευθεία γραμμή MN και σημαδέψουμε το σημείο C πάνω της, από αυτό το σημείο σχεδιάζουμε μια κάθετη SC στην ευθεία MN. Στη συνέχεια, θα υπερθέσουμε τη σωστή γωνία του τριγώνου ABC στη σωστή γωνία KSM, έτσι ώστε οι κορυφές τους να ευθυγραμμίζονται και το πόδι AC να πηγαίνει κατά μήκος της ακτίνας SC, μετά το σκέλος BC να πηγαίνει κατά μήκος της ακτίνας CM. Η ορθή γωνία του τριγώνου A'B'C' θα υπερτεθεί στη σωστή γωνία KCN έτσι ώστε οι κορυφές τους να είναι ευθυγραμμισμένες και το πόδι A'C' να πηγαίνει κατά μήκος της ακτίνας SK, μετά το σκέλος C'B' να πηγαίνει κατά μήκος της ακτίνας ΣΟ. Οι κορυφές Α και Α' θα συμπέσουν λόγω της ισότητας των σκελών AC και A'C'.
Τα τρίγωνα ABC και A'B'C' θα σχηματιστούν μαζί ισοσκελές τρίγωνο BAB’, στο οποίο AC θα είναι το ύψος και η διχοτόμος, και επομένως ο άξονας συμμετρίας του τριγώνου BAB’. Από αυτό προκύπτει ότι \(\Delta\)ABC = \(\Delta\)A’B’C’.
Αυτό το θεώρημα δίνει το 4ο κριτήριο για την ισότητα των ορθογωνίων τριγώνων (κατά υποτείνουσα και σκέλος).
Έτσι, όλα τα σημάδια της ισότητας των ορθογωνίων τριγώνων:
1. Αν δύο σκέλη ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με δύο σκέλη ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα2. Αν το σκέλος και η παρακείμενη οξεία γωνία ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με το σκέλος και την παρακείμενη οξεία γωνία ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα
3. Εάν το σκέλος και η αντίθετη οξεία γωνία ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με το σκέλος και την αντίθετη οξεία γωνία ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα
4. Αν η υποτείνουσα και η οξεία γωνία ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσες με την υποτείνουσα και την οξεία γωνία ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα
5. Αν το σκέλος και η υποτείνουσα ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με το σκέλος και την υποτείνουσα ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια ορθογώνια τρίγωνα είναι ίσα
Για να διαπιστωθεί η ισότητα των ορθογωνίων τριγώνων, αρκεί να γνωρίζουμε ότι δύο στοιχεία ενός τριγώνου είναι αντίστοιχα ίσα με δύο στοιχεία ενός άλλου τριγώνου (εξαιρουμένης της ορθής γωνίας). Αυτό, φυσικά, δεν ισχύει για την ισότητα δύο γωνιών ενός τριγώνου με δύο γωνίες ενός άλλου τριγώνου.
Από μέσα ορθογώνιο τρίγωνοη γωνία μεταξύ δύο σκελών είναι μια ευθεία γραμμή και οποιεσδήποτε δύο ορθές γωνίες είναι ίσες, τότε από το πρώτο σημάδι ισότητας των τριγώνων προκύπτει:
Εάν τα σκέλη ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με τα σκέλη ενός άλλου, τότε τέτοια τρίγωνα είναι ίσα (Εικ. 5).
Εάν το σκέλος και η γειτονική οξεία γωνία ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με το σκέλος και τη γειτονική γωνία ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα (Εικ. 6).

Ας εξετάσουμε δύο ακόμη σημάδια ισότητας ορθογωνίων τριγώνων.

ΘΕΩΡΗΜΑ . Εάν η υποτείνουσα και η οξεία γωνία ενός ορθογωνίου τριγώνου είναι ίσες με την υπότενουσα και την οξεία γωνία ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα (Εικ. 7).
ΑΠΟΔΕΙΞΗ. Από την ιδιότητα 1є § προκύπτει ότι σε τέτοια τρίγωνα οι άλλες δύο οξείες γωνίες είναι επίσης ίσες, επομένως τα τρίγωνα είναι ίσα σύμφωνα με το δεύτερο πρόσημο της ισότητας των τριγώνων, δηλαδή κατά μήκος της πλευράς (υποτείνουσα) και δύο γειτονικών γωνιών.
Q.E.D.
ΘΕΩΡΗΜΑ . Αν η υποτείνουσα και το σκέλος ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με την υποτείνουσα και το σκέλος ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.
ΑΠΟΔΕΙΞΗ. Ας σκεφτούμε τρίγωνα ABCκαι A 1 B 1 C 1 , των οποίων οι γωνίες C και C 1 είναι ορθές, AB = A 1 B 1 , BC = B 1 C 1 (Εικ. 8).

Επειδή< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с οξεία γωνίαΒ 1 Α 1 Γ 1). Αλλά αυτό είναι αδύνατο, επομένως οι κορυφές Α και Α 1 θα συμπέσουν. Επομένως, τα τρίγωνα ABC A 1 B 1 C 1 θα είναι απολύτως συμβατά, δηλαδή είναι ίσα.
Q.E.D.
Πυθαγόρειο θεώρημα
Η σημασία του έγκειται στο γεγονός ότι τα περισσότερα από τα θεωρήματα της γεωμετρίας μπορούν να συναχθούν από αυτό ή με τη βοήθειά του. Ένα από τα θεωρήματα καθιστά δυνατή την επαλήθευση ότι εάν μια κάθετη και κεκλιμένη ευθεία τραβιέται σε αυτήν από ένα σημείο εκτός ευθείας, τότε: α) οι κεκλιμένες ευθείες είναι ίσες εάν οι προβολές τους είναι ίσες. β) αυτό που είναι κεκλιμένο είναι μεγαλύτερο, που έχει μεγαλύτερη προβολή.
Το Πυθαγόρειο θεώρημα ήταν η πρώτη δήλωση που συσχέτισε τα μήκη των πλευρών των τριγώνων. Στη συνέχεια μάθαμε πώς να βρίσκουμε μήκη πλευρών και γωνίες οξείας και αμβλεία τρίγωνα. Αναπτύχθηκε όλη η επιστήμη της τριγωνομετρίας («τρίγωνο» σημαίνει «τρίγωνο» στα ελληνικά). Αυτή η επιστήμη έχει βρει εφαρμογή στην τοπογραφία. Αλλά και νωρίτερα, με τη βοήθειά του, έμαθαν να μετρούν φανταστικά τρίγωνα στον ουρανό, οι κορυφές των οποίων ήταν αστέρια. Τώρα η τριγωνομετρία χρησιμοποιείται ακόμη και για τη μέτρηση των αποστάσεων μεταξύ των διαστημικών σκαφών.
Χρησιμοποιώντας τις ιδιότητες των εμβαδών των πολυγώνων, θα δημιουργήσουμε τώρα μια αξιοσημείωτη σχέση μεταξύ της υποτείνουσας και των σκελών ενός ορθογωνίου τριγώνου. Το θεώρημα που θα αποδείξουμε ονομάζεται Πυθαγόρειο θεώρημα, το οποίο είναι το σημαντικότερο θεώρημα στη γεωμετρία.
Αν μας δοθεί ένα τρίγωνο,
Και με ορθή γωνία σε αυτό,
Αυτό είναι το τετράγωνο της υποτείνουσας
Μπορούμε πάντα εύκολα να βρούμε:
Τετράγωνουμε τα πόδια,
Βρίσκουμε το άθροισμα των δυνάμεων
Και μάλιστα με τόσο απλό τρόπο
Θα φτάσουμε στο αποτέλεσμα.
ΘΕΩΡΗΜΑ. Σε ένα ορθογώνιο τρίγωνο, το τετράγωνο της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των σκελών.
ΑΠΟΔΕΙΞΗ. Θεωρήστε ένα ορθογώνιο τρίγωνο με σκέλη a, b και c (Εικ. 9 α).

Ας αποδείξουμε ότι c 2 = a 2 + b 2 . Ας χτίσουμε το τρίγωνο σε τετράγωνο με πλευρά a+b, όπως φαίνεται στο σχήμα (Εικ. 9 β).
Το εμβαδόν ενός τέτοιου τετραγώνου με πλευρά a + b είναι ίσο με (a + b) 2. Από την άλλη πλευρά, αυτό το τετράγωνο αποτελείται από τέσσερα ίσα ορθογώνια τρίγωνα με εμβαδόν ab και ένα τετράγωνο με πλευρά c, άρα
Έτσι, (a + b) 2 =2ab + c 2, από όπου c 2 = a 2 + b 2.
Q.E.D.
ΣΥΜΠΕΡΑΣΜΑ 1 . Σε ένα ορθογώνιο τρίγωνο, οποιοδήποτε από τα σκέλη είναι μικρότερο από την υποτείνουσα.
ΑΠΟΔΕΙΞΗ. Σύμφωνα με το Πυθαγόρειο θεώρημα AB 2 = AC 2 + BC 2 . Αφού BC 2 >0, τότε AC 2<АВ, То есть АС<АВ.
ΣΥΜΠΕΡΑΣΜΑ 2. Για οποιαδήποτε οξεία γωνία β cosb<1.
ΑΠΟΔΕΙΞΗ. Εξ ορισμού του συνημιτόνου cosб = . Αλλά στο συμπέρασμα 1 αποδείχθηκε ότι το AC<АВ, Αυτό σημαίνει ότι το κλάσμα είναι μικρότερο από 1.
Τα ορθογώνια τρίγωνα των οποίων οι πλευρές εκφράζονται ως ακέραιοι ονομάζονται πυθαγόρεια τρίγωνα.
Μπορεί να αποδειχθεί ότι τα σκέλη a, b και η υποτείνουσα c τέτοιων τριγώνων εκφράζονται με τους τύπους a=2kmn. b=k(m2-n2); c=k(m 2 +n 2), όπου k, m και n είναι φυσικοί αριθμοί τέτοιοι ώστε m>n. Τα τρίγωνα με πλευρές των οποίων το μήκος είναι 3, 4, 5 ονομάζονται αιγυπτιακά τρίγωνα, επειδή ήταν γνωστά στους αρχαίους Αιγύπτιους.
Συνομιλία με το Πυθαγόρειο θεώρημα.
Αν το τετράγωνο της μιας πλευράς ενός τριγώνου είναι ίσο με το άθροισμα των τετραγώνων των άλλων δύο πλευρών, τότε το τρίγωνο είναι ορθογώνιο (σημάδι ορθογωνίου τριγώνου).
ΑΠΟΔΕΙΞΗ.
Έστω τρίγωνο ABC AB 2 = AC 2 + BC 2. Ας αποδείξουμε ότι η γωνία C είναι ορθή. Θεωρήστε ένα ορθογώνιο τρίγωνο A 1 B 1 C 1 με ορθή γωνία C 1, στο οποίο A 1 C 1 = AC και B 1 C 1 = BC. Με το Πυθαγόρειο θεώρημα A 1 B 1 2 =A 1 C 1 2 +B 1 C 1 2, και επομένως A 1 B 1 2 = AC 2 +BC 2. Αλλά AC 2 + BC 2 = AB 2 σύμφωνα με το θεώρημα. Επομένως, A 1 B 1 2 = AB 2, από όπου A 1 B 1 = AB. Επομένως, τα τρίγωνα ABC και A 1 B 1 C 1 είναι ίσα σε τρεις πλευρές< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.
Q.E.D.
Τα ορθογώνια τρίγωνα, μαζί με τα ισοσκελή και τα ισόπλευρα τρίγωνα, παίρνουν τη θέση τους ανάμεσα στα τρίγωνα, κατέχοντας ένα ειδικό σύνολο ειδικών ιδιοτήτων που χαρακτηρίζουν μόνο αυτόν τον τύπο τριγώνων. Ας εξετάσουμε αρκετά θεωρήματα για την ισότητα των ορθογωνίων τριγώνων, τα οποία θα απλοποιήσουν σημαντικά τη λύση ορισμένων προβλημάτων.
Το πρώτο σημάδι ισότητας ορθογωνίων τριγώνων
Τα σημάδια της ισότητας των ορθογωνίων τριγώνων προέρχονται από τα τρία σημάδια της ισότητας των τριγώνων, αλλά μια ορθή γωνία τα παραμορφώνει, διευρύνοντάς τα ενώ τα κάνει απλούστερα. Οποιοδήποτε από τα σημάδια ισότητας ορθογωνίων τριγώνων μπορεί να αντικατασταθεί από ένα από τα τρία κύρια, αλλά αυτό θα πάρει πολύ χρόνο, επομένως έχουν εντοπιστεί 5 ιδιότητες και σημάδια ισότητας ορθογωνίων τριγώνων.
Πολύ συχνά, αντί να χρησιμοποιούνται τα βασικά σημάδια της ισότητας των τριγώνων, χρησιμοποιείται η μέθοδος υπέρθεσης, όταν δύο σχήματα υπερτίθενται νοερά το ένα πάνω στο άλλο. Δεν μπορεί να ειπωθεί ότι αυτό είναι αλήθεια ή ψευδές. Απλά μια άλλη μέθοδος απόδειξης που πρέπει να εξετάσετε. Αλλά δεν μπορεί κανείς να σκεφτεί ότι οποιοδήποτε σημάδι μπορεί να αποδειχθεί με συνηθισμένη υπέρθεση. Γι' αυτό θα εξετάσουμε την απόδειξη των σημείων ισότητας ορθογωνίων τριγώνων μέσω των τριών βασικών πρόσημων ισότητας τριγώνων.
Το πρώτο σημάδι ισότητας ορθογωνίων τριγώνων λέει: δύο ορθογώνια τρίγωνα είναι ίσα αν δύο σκέλη ενός τριγώνου είναι ίσα με δύο σκέλη ενός άλλου τριγώνου. Εν ολίγοις, αυτό το χαρακτηριστικό ονομάζεται ισότητα σε δύο πλευρές.

Ρύζι. 1. Ισότητα σε δύο πλευρές
Η απόδειξη αυτού του σημείου είναι πολύ απλή. Δίνονται: δύο σκέλη ενός ορθογωνίου τριγώνου είναι ίσα. Μεταξύ των ποδιών υπάρχει μια ορθή γωνία, η οποία είναι ίση με 90 μοίρες, που σημαίνει ότι η γωνία των τριγώνων συμπίπτει. Επομένως, δύο τρίγωνα είναι ίσα σε δύο πλευρές και τη γωνία μεταξύ τους.
Δεύτερο σημάδι
Το δεύτερο σημάδι έχει ως εξής: δύο ορθογώνια τρίγωνα είναι ίσα αν το σκέλος και η παρακείμενη οξεία γωνία ενός τριγώνου είναι ίσα με το σκέλος και η γειτονική γωνία του άλλου τριγώνου.
Το δεύτερο πρόσημο αποδεικνύεται με βάση την ίδια δήλωση σχετικά με την ισότητα των ορθών γωνιών μεταξύ τους. Εάν τα τρίγωνα έχουν ίσα σκέλη, οι οξείες γωνίες τους είναι ίσες και οι ορθές γωνίες είναι εξ ορισμού ίσες, τότε τέτοια τρίγωνα είναι ίσα σύμφωνα με το δεύτερο πρόσημο ισότητας (πλευρές και δύο παρακείμενες γωνίες).
Τρίτο σημάδι
Δύο ορθογώνια τρίγωνα είναι ίσα αν η πλευρά και η απέναντι οξεία γωνία είναι ίσες.

Ρύζι. 2. Σχέδιο για απόδειξη
Το άθροισμα των οξειών γωνιών σε ένα τρίγωνο είναι 90 μοίρες. Ας υποδηλώσουμε τις γωνίες με μικρά λατινικά γράμματα για απλότητα απόδειξης. Η μία γωνία είναι ορθή και οι άλλες δύο χαρακτηρίζονται από τα γράμματα a και b στο πρώτο τρίγωνο. γ και δ στο δεύτερο τρίγωνο.
Οι γωνίες a και d είναι ίσες μεταξύ τους σύμφωνα με τις συνθήκες του προβλήματος.
Αφαιρέστε τη γωνία α και από τις δύο πλευρές της παράστασης
Δηλαδή, αν σε δύο ορθογώνια τρίγωνα δύο οξείες γωνίες είναι ίσες μεταξύ τους, τότε και οι άλλες δύο οξείες γωνίες θα είναι επίσης ίσες και μπορούμε να χρησιμοποιήσουμε το δεύτερο πρόσημο.
Στο δεύτερο και το τρίτο ζώδιο, πρέπει να εστιάσετε ιδιαίτερα στην οξεία γωνία, καθώς οι ορθές γωνίες είναι πάντα ίσες μεταξύ τους.
Τέταρτο σημάδι
Αν η υποτείνουσα και μια οξεία γωνία ενός ορθογωνίου τριγώνου είναι ίσες με την υποτείνουσα και μια οξεία γωνία ενός άλλου ορθογωνίου τριγώνου, τότε τα τρίγωνα είναι ίσα.
Όπως αναφέρθηκε στο προηγούμενο σημάδι: εάν μια οξεία γωνία ενός ορθογωνίου τριγώνου είναι ίση με την αντίστοιχη οξεία γωνία ενός άλλου ορθογωνίου τριγώνου, τότε το άλλο ζεύγος οξειών γωνιών τριγώνων θα είναι ίσο μεταξύ τους.
Αυτό σημαίνει ότι, σύμφωνα με τις συνθήκες αυτού του κριτηρίου, έχουμε ισότητα της υποτείνουσας και δύο οξείες γωνίες τριγώνων, που σημαίνει ότι τέτοια τρίγωνα θα είναι ίσα σε πλευρές και δύο παρακείμενες γωνίες (2ο πρόσημο ισότητας τριγώνων)
Πέμπτο σημάδι
Αν η υποτείνουσα και το σκέλος ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με την υποτείνουσα και το σκέλος ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.
Εάν η υποτείνουσα και το σκέλος δύο τριγώνων είναι αντίστοιχα ίσα, τότε τα δεύτερα σκέλη τέτοιων τριγώνων θα είναι ίσα μεταξύ τους. Αυτό πηγάζει από το Πυθαγόρειο θεώρημα.

Ρύζι. 3. Ισότητα κατά μήκος του ποδιού και της υποτείνουσας
Το τετράγωνο της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των ποδιών. Οι υποτείνουσες είναι ίσες μεταξύ τους, το σκέλος του ενός τριγώνου είναι ίσο με το τετράγωνο του άλλου τριγώνου, που σημαίνει ότι το άθροισμα παραμένει αληθές και τα άλλα δύο σκέλη θα είναι ίσα μεταξύ τους.
Τι μάθαμε;
Εξετάσαμε την απόδειξη των πέντε τεστ για την ισότητα των τριγώνων μέσα από τα βασικά τεστ για την ισότητα των τριγώνων. Καταλάβαμε γιατί μια τέτοια απόδειξη είναι προτιμότερη από μια επικάλυψη και καθορίσαμε μια διαδρομή απόδειξης που θα σας επιτρέψει να επαναφέρετε τις βασικές έννοιες του θέματος στη μνήμη ανά πάσα στιγμή, χωρίς περιττή απομνημόνευση.
Δοκιμή για το θέμα
Βαθμολογία άρθρου
Μέση βαθμολογία: 4.6. Συνολικές βαθμολογίες που ελήφθησαν: 100.
Ας θυμηθούμε από την ύλη του προηγούμενου μαθήματος ότι ένα τρίγωνο ονομάζεται ορθογώνιο τρίγωνο εάν τουλάχιστον μία από τις γωνίες του είναι ορθή (δηλαδή ίση με 90°).
Ας σκεφτούμε πρώτο σημάδιΙσότητα τριγώνων: αν δύο σκέλη ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με δύο σκέλη ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.
Ας δείξουμε αυτή την περίπτωση:
Ρύζι. 1. Ίσα ορθογώνια τρίγωνα
Απόδειξη:
Ας θυμηθούμε την πρώτη ισότητα αυθαίρετων τριγώνων.

Ρύζι. 2
Αν δύο πλευρές και η γωνία μεταξύ τους ενός τριγώνου και των αντίστοιχων δύο πλευρών και η μεταξύ τους γωνία του δεύτερου τριγώνου είναι ίσες, τότε αυτά τα τρίγωνα είναι ίσα. Αυτό υποδεικνύεται από το πρώτο σημάδι ισότητας τριγώνων, δηλαδή:

Μια παρόμοια απόδειξη ακολουθεί για τα ορθογώνια τρίγωνα:
 .
.
Τα τρίγωνα είναι ίσα σύμφωνα με το πρώτο κριτήριο.
Ας εξετάσουμε το δεύτερο πρόσημο της ισότητας των ορθογωνίων τριγώνων. Εάν το σκέλος και η παρακείμενη οξεία γωνία ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσα με το σκέλος και την παρακείμενη οξεία γωνία ενός άλλου ορθογωνίου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.

Ρύζι. 3
Απόδειξη:

Ρύζι. 4
Ας χρησιμοποιήσουμε το δεύτερο κριτήριο για την ισότητα των τριγώνων:

Παρόμοια απόδειξη για ορθογώνια τρίγωνα:

Τα τρίγωνα είναι ίσα σύμφωνα με το δεύτερο κριτήριο.
Ας εξετάσουμε το τρίτο κριτήριο για την ισότητα των ορθογωνίων τριγώνων: αν η υποτείνουσα και η γειτονική γωνία ενός ορθογωνίου τριγώνου είναι αντίστοιχα ίσες με την υποτείνουσα και τη διπλανή γωνία ενός άλλου τριγώνου, τότε τέτοια τρίγωνα είναι ίσα.
Απόδειξη:

Ρύζι. 5
Ας θυμηθούμε το δεύτερο κριτήριο για την ισότητα των τριγώνων:

Ρύζι. 6
Αυτά τα τρίγωνα είναι ίσα αν:

Εφόσον είναι γνωστό ότι ένα ζεύγος οξειών γωνιών σε ορθογώνια τρίγωνα είναι ίσο με (∠A = ∠A 1), τότε η ισότητα του άλλου ζεύγους γωνιών (∠B = ∠B 1) αποδεικνύεται ως εξής:
Αφού AB = A 1 B 1 (κατά συνθήκη), ∠B = ∠B 1, ∠A = ∠A 1. Επομένως, τα τρίγωνα ABC και A 1 B 1 C 1 είναι ίσα σύμφωνα με το δεύτερο κριτήριο.
Εξετάστε το ακόλουθο κριτήριο για την ισότητα των τριγώνων:
Αν το σκέλος και η υποτείνουσα ενός τριγώνου είναι αντίστοιχα ίσα με το σκέλος και την υποτείνουσα ενός άλλου τριγώνου, αυτά τα ορθογώνια τρίγωνα είναι ίσα.

Ρύζι. 7
Απόδειξη:
Ας συνδυάσουμε τα τρίγωνα ABC και A 1 B 1 C 1 επικαλύπτοντας. Ας υποθέσουμε ότι οι κορυφές A και A 1, καθώς και C και C 1 υπερτίθενται, αλλά η κορυφή B και το σημείο B 1 δεν συμπίπτουν. Αυτή ακριβώς είναι η περίπτωση που φαίνεται στο παρακάτω σχήμα:

Ρύζι. 8
Σε αυτή την περίπτωση, μπορούμε να παρατηρήσουμε το ισοσκελές τρίγωνο ABV 1 (εξ ορισμού - από τη συνθήκη AB = AB 1). Επομένως, σύμφωνα με την ιδιότητα, ∠AB 1 B = ∠ABV 1. Ας δούμε τον ορισμό της εξωτερικής γωνίας. Εξωτερική γωνίαενός τριγώνου είναι η γωνία που γειτνιάζει με οποιαδήποτε γωνία του τριγώνου. Το μέτρο της μοίρας του είναι ίσο με το άθροισμα δύο γωνιών ενός τριγώνου που δεν γειτνιάζουν με αυτό. Το σχήμα δείχνει αυτή την αναλογία:

Ρύζι. 9
Η γωνία 5 είναι η εξωτερική γωνία του τριγώνου και ισούται με ∠5 = ∠1 + ∠2. Επομένως, μια εξωτερική γωνία είναι μεγαλύτερη από καθεμία από τις γωνίες που δεν γειτνιάζουν με αυτήν.
Έτσι, ∠ABB 1 είναι η εξωτερική γωνία για το τρίγωνο ABC και ισούται με το άθροισμα ∠ABB 1 = ∠CAB + ∠ACB = ∠ABC = ∠CAB + 90 o. Έτσι, η ∠AB 1 B (που είναι οξεία γωνία στο ορθογώνιο τρίγωνο ABC 1) δεν μπορεί να είναι ίση με τη γωνία ∠ABB 1, επειδή αυτή η γωνία είναι αμβλεία σύμφωνα με όσα έχουν αποδειχθεί.
Αυτό σημαίνει ότι η υπόθεσή μας σχετικά με τη θέση των σημείων Β και Β 1 αποδείχθηκε λανθασμένη, επομένως αυτά τα σημεία συμπίπτουν. Αυτό σημαίνει ότι τα τρίγωνα ABC και A 1 B 1 C 1 υπερτίθενται. Επομένως είναι ίσοι (εξ ορισμού).
Έτσι, αυτά τα χαρακτηριστικά δεν εισάγονται μάταια, επειδή μπορούν να χρησιμοποιηθούν για την επίλυση ορισμένων προβλημάτων.
- Κρατικό Πανεπιστήμιο του Ομσκ ().
- Πύλη βοήθειας calc.ru ().
- Πύλη δασκάλων ().
1. Αρ. 38. Butuzov V.F., Kadomtsev S.B., Prasolov V.V., επιμέλεια Sadovnichy V.A. Geometry 7. Μ.: Εκπαίδευση. 2010
2. Με βάση τα δεδομένα που υποδεικνύονται στο σχήμα, υποδείξτε ίσα τρίγωνα, εάν υπάρχουν.

3. Με βάση τα δεδομένα που υποδεικνύονται στο σχήμα, υποδείξτε ίσα τρίγωνα, εάν υπάρχουν. Λάβετε υπόψη ότι AC = AF.

4. Σε ένα ορθογώνιο τρίγωνο, η διάμεσος και το υψόμετρο σύρονται στην υποτείνουσα. Η γωνία μεταξύ τους είναι 20 o. Προσδιορίστε το μέγεθος καθεμιάς από τις οξείες γωνίες αυτού του ορθογωνίου τριγώνου.
Ενότητες: Μαθηματικά
Θέμα: «Σήματα για την ισότητα των ορθογωνίων τριγώνων»
Στόχος: εμπέδωση γνώσεων (ιδιότητες ορθογωνίων τριγώνων), εξοικείωση με κάποια σημάδια ισότητας ορθογωνίων τριγώνων.
Κατά τη διάρκεια των μαθημάτων:
Ι. Οργανωτική στιγμή.II. Προφορικά.
1. Απαντήστε στις ερωτήσεις:
- Ονομάστε τα στοιχεία ενός ορθογώνιου τριγώνου.
- Ποιες ιδιότητες έχουν τα στοιχεία ενός ορθογωνίου τριγώνου;
- Να αποδείξετε ότι το σκέλος ενός ορθογωνίου τριγώνου που βρίσκεται απέναντι από μια γωνία 30 0 είναι ίσο με το μισό της υποτείνουσας.
- Αποδείξτε ότι αν ένα σκέλος ενός ορθογωνίου τριγώνου είναι ίσο με το μισό της υποτείνουσας, τότε η γωνία απέναντι από αυτό το σκέλος είναι ίση με 30 0.
- Βρείτε το x. Επιλέξτε την απάντηση από το τρίγωνο. Τα γράμματα μιας λέξης βρίσκονται στους τομείς του τριγώνου. Συζήτηση σε ζευγάρια (3 λεπτά).
Εικόνα 1.
Έφτιαξαν τη λέξη «σημάδι».
III. Εκμάθηση νέου υλικούΜελετώντας τα τρίγωνα λέμε ότι έχει ορισμένες ιδιότητες και χαρακτηριστικά. Ποια σημάδια ισότητας τριγώνων γνωρίζετε; Διατυπώσαμε και αποδείξαμε τις ιδιότητες των ορθογωνίων τριγώνων και σήμερα θα δούμε τα σημάδια ισότητας των ορθογωνίων τριγώνων και θα λύσουμε προβλήματα χρησιμοποιώντας τα.
Κατά την απόδειξη της ισότητας των τριγώνων, πόσα ζεύγη αντίστοιχα ίσων στοιχείων βρέθηκαν; Είναι δυνατόν να αποδειχθεί η ισότητα των ορθογωνίων τριγώνων κατά μήκος δύο πλευρών;
Μπροστά σας υπάρχουν δύο ορθογώνια τρίγωνα ABC και A 1 B 1 C 1, τα πόδια τους είναι αντίστοιχα ίσα. Αποδείξτε, αν είναι δυνατόν, την ισότητα τους.
Νο 1. (Σε δύο πλευρές)

Σχήμα 2.
Δίνονται: ABC και A 1 B 1 C 1, B=B 1 =90 0, AB = A 1 B 1, BC = B 1 C 1
Απόδειξη: ABC = A 1 B 1 C 1
Πώς θα ακούγεται η πινακίδα; (Στη συνέχεια, εργασία Νο. 1)
Νο 2. (Σύμφωνα με το πόδι και την οξεία γωνία που γειτνιάζει)

Εικόνα 3.
Δίνονται: ABC και A 1 B 1 C 1, B=B 1 =90 0, BC = B 1 C 1, C= C 1
Απόδειξη: ABC = A 1 B 1 C 1
Πώς θα ακούγεται η πινακίδα; (Στη συνέχεια, εργασία Νο. 2)
Νο. 3. (Με υποτείνουσα και οξεία γωνία)

Εικόνα 4.
Δίνονται: ABC και A 1 B 1 C 1, B=B 1 =90 0, AC = A 1 C 1, A= A 1
Απόδειξη: ABC = A 1 B 1 C 1
Πώς θα ακούγεται η πινακίδα; (Στη συνέχεια, εργασία Νο. 3)
Καθήκοντα. Να βρείτε ίσα τρίγωνα και να αποδείξετε την ισότητά τους.

Εικόνα 5.
IV. Ενίσχυση όσων μάθαμε στο μάθημα.Λύστε το παρακάτω πρόβλημα.

Εικόνα 6.
Δίνονται: ABC, A 1 B 1 C 1, DAB=CBA=90 0, AD = BD
Απόδειξη: CAB=DBA.
Συζήτηση σε ομάδες των τεσσάρων (3 λεπτά).
Γιατί πρόβλημα από το σχολικό βιβλίο Νο 261 με ηχογράφηση.

Εικόνα 7.
Δίνονται: ABC – ισοσκελές, AD και CE – ύψος του ABC
Απόδειξη: AD = CE
Απόδειξη:
V. Ανάθεση εργασίας για το σπίτι.
Π.35 (τρία ζώδια), Νο. 261 (αποδείξετε ότι το AOS είναι ισοσκελές), Νο. 268 (δοκιμή ισότητας ορθογωνίων τριγώνων κατά μήκος σκέλους και αντίθετης γωνίας).
Στο επόμενο μάθημα γεωμετρίας θα συνεχίσουμε τη γνωριμία μας με τα σημάδια ισότητας ορθογωνίων τριγώνων. Θα βαθμολογήσω και την επόμενη φορά με βάση τα αποτελέσματα για 2 μαθήματα.
Επιπροσθέτως. Βρείτε ίσα τρίγωνα.