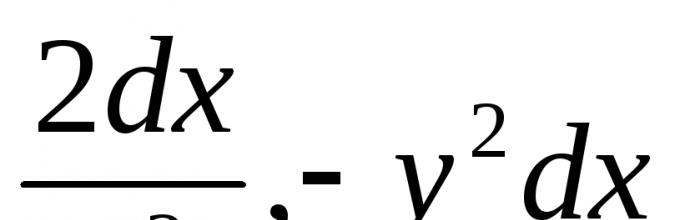Η εξίσωση Μ(Χ, y) dx+ Ν(Χ, y) dy=0 ονομάζεται γενικευμένη ομοιογενής εάν είναι δυνατόν να επιλεγεί ένας τέτοιος αριθμός κ, ότι η αριστερή πλευρά αυτής της εξίσωσης γίνεται ομοιογενής συνάρτηση κάποιου βαθμού Μ σχετικά Χ, y, dx Και dy υπό την προϋπόθεση ότι Χ θεωρείται η τιμή της πρώτης διάστασης, y – κ‑ ου μετρήσεις , dx Και dy – αντίστοιχα μηδέν και (κ-1) ου μετρήσεις. Για παράδειγμα, αυτή θα ήταν η εξίσωση. (6.1)

Ισχύει σύμφωνα με τις παραδοχές που έγιναν σχετικά με τις μετρήσεις

Χ, y, dx Και dy μέλη της αριστερής πλευράς
Και dy θα έχει διαστάσεις -2, 2 αντίστοιχα κΚαι κ-1. Εξισώνοντάς τα, λαμβάνουμε μια συνθήκη που πρέπει να ικανοποιεί ο απαιτούμενος αριθμός κ: -2 = 2κ = κ-1. Αυτή η προϋπόθεση ικανοποιείται όταν κ = -1 (με αυτό κόλοι οι όροι στην αριστερή πλευρά της εξίσωσης που εξετάζουμε θα έχουν διάσταση -2). Κατά συνέπεια, η εξίσωση (6.1) είναι γενικευμένη ομοιογενής.

Η γενικευμένη ομοιογενής εξίσωση ανάγεται σε μια εξίσωση με χωριστές μεταβλητές χρησιμοποιώντας αντικατάσταση
, Οπου z– νέα άγνωστη λειτουργία. Ας ολοκληρώσουμε την εξίσωση (6.1) χρησιμοποιώντας την υποδεικνυόμενη μέθοδο. Επειδή κ = -1, λοιπόν
, μετά την οποία παίρνουμε την εξίσωση.

Ενσωματώνοντάς το, βρίσκουμε
, που
. Αυτή είναι μια γενική λύση της εξίσωσης (6.1).

§ 7. Γραμμικές διαφορικές εξισώσεις 1ης τάξης.

Μια γραμμική εξίσωση 1ης τάξης είναι μια εξίσωση που είναι γραμμική ως προς την επιθυμητή συνάρτηση και την παράγωγό της. Μοιάζει:

, (7.1)

Οπου Π(Χ) Και Q(Χ) – δίνονται συνεχείς συναρτήσεις του Χ. Εάν η συνάρτηση
, τότε η εξίσωση (7.1) έχει τη μορφή:
(7.2)

και ονομάζεται γραμμική ομοιογενής εξίσωση, αλλιώς
ονομάζεται γραμμική ανομοιογενής εξίσωση.

Η γραμμική ομοιογενής διαφορική εξίσωση (7.2) είναι μια εξίσωση με χωριστές μεταβλητές:

(7.3)

Η έκφραση (7.3) είναι η γενική λύση της εξίσωσης (7.2). Να βρεθεί μια γενική λύση της εξίσωσης (7.1), στην οποία η συνάρτηση Π(Χ) δηλώνει την ίδια συνάρτηση με την εξίσωση (7.2), εφαρμόζουμε μια τεχνική που ονομάζεται μέθοδος μεταβολής μιας αυθαίρετης σταθεράς και αποτελείται από τα εξής: θα προσπαθήσουμε να επιλέξουμε τη συνάρτηση C=C(Χ) έτσι ώστε η γενική λύση της γραμμικής ομογενούς εξίσωσης (7.2) να είναι λύση της ανομοιογενούς γραμμικής εξίσωσης (7.1). Τότε για την παράγωγο της συνάρτησης (7.3) λαμβάνουμε:

.

Αντικαθιστώντας την ευρεθείσα παράγωγο στην εξίσωση (7.1), θα έχουμε:

ή
.

Οπου
, Οπου - αυθαίρετη σταθερά. Ως αποτέλεσμα, η γενική λύση στην ανομοιογενή γραμμική εξίσωση (7.1) θα είναι (7.4)

Ο πρώτος όρος σε αυτόν τον τύπο αντιπροσωπεύει τη γενική λύση (7.3) της γραμμικής ομοιογενούς διαφορικής εξίσωσης (7.2) και ο δεύτερος όρος του τύπου (7.4) είναι μια συγκεκριμένη λύση της γραμμικής ανομοιογενούς εξίσωσης (7.1), που προκύπτει από τη γενική ( 7.4) με
. Τονίζουμε αυτό το σημαντικό συμπέρασμα με τη μορφή ενός θεωρήματος.

Θεώρημα.Εάν είναι γνωστή μια συγκεκριμένη λύση μιας γραμμικής ανομοιογενούς διαφορικής εξίσωσης
, τότε όλες οι άλλες λύσεις έχουν τη μορφή
, Οπου
- γενική λύση της αντίστοιχης γραμμικής ομογενούς διαφορικής εξίσωσης.

Ωστόσο, πρέπει να σημειωθεί ότι για την επίλυση της γραμμικής ανομοιογενούς διαφορικής εξίσωσης της 1ης τάξης (7.1), χρησιμοποιείται συχνότερα μια άλλη μέθοδος, που μερικές φορές ονομάζεται μέθοδος Bernoulli. Θα αναζητήσουμε τη λύση της εξίσωσης (7.1) στη μορφή
. Επειτα
. Ας αντικαταστήσουμε την ευρεθείσα παράγωγο στην αρχική εξίσωση:
.

Ας συνδυάσουμε, για παράδειγμα, τον δεύτερο και τον τρίτο όρο της τελευταίας παράστασης και ας εξαγάγουμε τη συνάρτηση u(Χ) πίσω από την αγκύλη:
(7.5)

Απαιτούμε να ακυρωθεί η παρένθεση:
.

Ας λύσουμε αυτήν την εξίσωση θέτοντας μια αυθαίρετη σταθερά ντο ίσο με μηδέν:
. Με τη συνάρτηση που βρέθηκε v(Χ) Ας επιστρέψουμε στην εξίσωση (7.5):
.

Λύνοντάς το, παίρνουμε:
.

Συνεπώς, η γενική λύση της εξίσωσης (7.1) έχει τη μορφή.

def 1 Τύπος DU

που ονομάζεται ομοιογενής διαφορική εξίσωση πρώτης τάξης(ODU).

Θ 1 Ας πληρούνται οι ακόλουθες προϋποθέσεις για τη συνάρτηση:

1) συνεχής στο

Τότε η ODE (1) έχει ένα γενικό ολοκλήρωμα, το οποίο δίνεται από τον τύπο:

όπου υπάρχει κάποιο αντιπαράγωγο της συνάρτησης Μεείναι μια αυθαίρετη σταθερά.

Σημείωση 1Εάν για κάποιους ικανοποιείται η προϋπόθεση, τότε κατά τη διαδικασία επίλυσης του ODE (1) μπορεί να χαθούν λύσεις της φόρμας· τέτοιες περιπτώσεις πρέπει να αντιμετωπίζονται πιο προσεκτικά και καθεμία από αυτές πρέπει να ελεγχθεί ξεχωριστά.

Έτσι από το θεώρημα Θ1πρέπει γενικός αλγόριθμος για την επίλυση ODE (1):

1) Κάντε μια αντικατάσταση:

2) Έτσι, θα προκύψει μια διαφορική εξίσωση με χωριστές μεταβλητές, οι οποίες θα πρέπει να ενσωματωθούν.

3) Επιστροφή στις παλιές gvariables.

4) Ελέγξτε τις τιμές για τη συμμετοχή τους στη λύση γνήσιο τηλεχειριστήριο, υπό την οποία θα πληρούται η προϋπόθεση

5) Γράψτε την απάντηση.

Παράδειγμα 1Λύστε ΔΕ (4).

Λύση:Η DE (4) είναι μια ομοιογενής διαφορική εξίσωση, αφού έχει τη μορφή (1). Ας κάνουμε μια αλλαγή (3), αυτό θα φέρει την εξίσωση (4) στη μορφή:

Η εξίσωση (5) είναι το γενικό ολοκλήρωμα του DE (4).

Σημειώστε ότι κατά το διαχωρισμό μεταβλητών και τη διαίρεση με, οι λύσεις θα μπορούσαν να χαθούν, αλλά αυτή δεν είναι μια λύση στο DE (4), η οποία επαληθεύεται εύκολα με άμεση αντικατάσταση στην ισότητα (4), καθώς αυτή η τιμή δεν περιλαμβάνεται στον τομέα ορισμού της αρχικής ΔΕ.

Απάντηση:

Σημείωση 2Μερικές φορές μπορείτε να γράψετε ODE με όρους διαφορών μεταβλητών ΧΚαι u.Συνιστάται να μετακινηθείτε από αυτή τη σημείωση του τηλεχειριστηρίου στην έκφραση μέσω της παραγώγου και μόνο τότε να πραγματοποιήσετε την αντικατάσταση (3).

Διαφορικές εξισώσεις ανάγονται σε ομοιογενείς.

def 2 Η συνάρτηση καλείται ομοιογενής συνάρτηση βαθμού κ στην περιοχή, για την οποία θα ικανοποιηθεί η ισότητα:

Εδώ είναι οι πιο συνηθισμένοι τύποι διαφορικών εξισώσεων που μπορούν να αναχθούν σε σχηματισμό (1) μετά από διάφορους μετασχηματισμούς.

1) πού είναι η συνάρτηση είναι ομοιογενής, βαθμός μηδέν, δηλαδή ισχύει η ισότητα: Η DE (6) ανάγεται εύκολα στη μορφή (1), αν βάλουμε , η οποία ενσωματώνεται περαιτέρω χρησιμοποιώντας την αντικατάσταση (3).

2) (7), όπου οι συναρτήσεις είναι ομοιογενείς του ίδιου βαθμού κ . Η DE της μορφής (7) ενσωματώνεται επίσης χρησιμοποιώντας την αντικατάσταση (3).

Παράδειγμα 2Λύστε ΔΕ (8).

Λύση:Ας δείξουμε ότι η DE (8) είναι ομοιογενής. Ας διαιρέσουμε με το τι είναι δυνατό, αφού δεν είναι λύση στο ΔΕ (8).

Ας κάνουμε μια αλλαγή (3), αυτή θα φέρει την εξίσωση (9) στη μορφή:

Η εξίσωση (10) είναι το γενικό ολοκλήρωμα του DE (8).

Σημειώστε ότι κατά τον διαχωρισμό μεταβλητών και τη διαίρεση με, θα μπορούσαν να χαθούν λύσεις που αντιστοιχούν στις τιμές των και. Ας ελέγξουμε αυτές τις εκφράσεις. Ας τα αντικαταστήσουμε σε DE (8):



Απάντηση:

Είναι ενδιαφέρον να σημειωθεί ότι κατά την επίλυση αυτού του παραδείγματος, εμφανίζεται μια συνάρτηση που ονομάζεται "σύμβολο" του αριθμού Χ(διαβάζει " signum x"), που ορίζεται από την έκφραση:

Σημείωση 3Η μείωση του DE (6) ή (7) στη μορφή (1) δεν είναι απαραίτητη· εάν είναι προφανές ότι το DE είναι ομοιογενές, τότε μπορείτε να κάνετε αμέσως την αντικατάσταση

3) Ένα DE της μορφής (11) ενσωματώνεται ως ODE εάν , και η αντικατάσταση εκτελείται αρχικά:

(12), πού είναι η λύση του συστήματος: (13) και στη συνέχεια χρησιμοποιήστε την αντικατάσταση (3) για τη συνάρτηση. Αφού λάβουν το γενικό ολοκλήρωμα, επιστρέφουν στις μεταβλητές ΧΚαι στο.

Εάν , τότε, υποθέτοντας στην εξίσωση (11), λαμβάνουμε μια διαφορική εξίσωση με χωριστές μεταβλητές.

Παράδειγμα 3Λύστε το πρόβλημα Cauchy (14).

Λύση:Ας δείξουμε ότι το DE (14) ανάγεται σε ένα ομοιογενές DE και ενσωματώνεται σύμφωνα με το παραπάνω σχήμα:

Ας λύσουμε το ανομοιογενές σύστημα γραμμικών αλγεβρικών εξισώσεων (15) χρησιμοποιώντας τη μέθοδο Cramer:

Ας κάνουμε μια αλλαγή μεταβλητών και ας ενσωματώσουμε την εξίσωση που προκύπτει:

(16) – Γενικό ολοκλήρωμα ΔΕ (14). Κατά τον διαχωρισμό μεταβλητών, οι λύσεις θα μπορούσαν να χαθούν κατά τη διαίρεση με μια παράσταση, η οποία θα μπορούσε να ληφθεί ρητά μετά την επίλυση της τετραγωνικής εξίσωσης. Ωστόσο, λαμβάνονται υπόψη στο γενικό ολοκλήρωμα (16) στο

Ας βρούμε μια λύση στο πρόβλημα Cauchy: αντικαταστήστε τις τιμές και στο γενικό ολοκλήρωμα (16) και βρείτε Με.

Έτσι, το μερικό ολοκλήρωμα θα δοθεί από τον τύπο:

Απάντηση:

4) Είναι δυνατό να αναχθούν ορισμένες διαφορικές εξισώσεις σε ομοιογενείς για μια νέα, ακόμη άγνωστη συνάρτηση, εάν εφαρμόσουμε μια αντικατάσταση της μορφής:

Σε αυτή την περίπτωση ο αριθμός Μεπιλέγεται από την προϋπόθεση ότι η εξίσωση που προκύπτει, αν είναι δυνατόν, γίνεται ομοιογενής σε κάποιο βαθμό. Ωστόσο, εάν αυτό δεν μπορεί να γίνει, τότε η υπό εξέταση ΔΕ δεν μπορεί να αναχθεί σε ομοιογενή με αυτόν τον τρόπο.

Παράδειγμα 4Λύστε DE. (18)

Λύση:Ας δείξουμε ότι το DE (18) ανάγεται σε ένα ομοιογενές DE χρησιμοποιώντας την υποκατάσταση (17) και ενσωματώνεται περαιτέρω χρησιμοποιώντας την υποκατάσταση (3):

Ας βρούμε Με:

Έτσι, μια συγκεκριμένη λύση της ΔΕ (24) έχει τη μορφή

.
Διαφορικές εξισώσεις.

§ 1. Βασικές έννοιες για συνηθισμένες διαφορικές εξισώσεις.

Ορισμός 1.Συνήθης διαφορική εξίσωση n– η σειρά για τη συνάρτηση yδιαφωνία Χονομάζεται σχέση της μορφής

Οπου φά– μια δεδομένη συνάρτηση των επιχειρημάτων του. Στο όνομα αυτής της κατηγορίας μαθηματικών εξισώσεων, ο όρος «διαφορικό» τονίζει ότι περιλαμβάνουν παράγωγα
(συναρτήσεις που σχηματίζονται ως αποτέλεσμα διαφοροποίησης). Ο όρος «συνήθης» υποδηλώνει ότι η επιθυμητή συνάρτηση εξαρτάται μόνο από ένα πραγματικό όρισμα.

Μια συνηθισμένη διαφορική εξίσωση μπορεί να μην περιέχει ρητό όρισμα Χ, την απαιτούμενη λειτουργία
και οποιοδήποτε από τα παράγωγά του, αλλά το υψηλότερο παράγωγο
πρέπει να περιλαμβάνεται στην εξίσωση n- η σειρά. Για παράδειγμα

ΕΝΑ)
– εξίσωση πρώτης τάξης.

σι)
– εξίσωση τρίτης τάξης.

Κατά τη σύνταξη συνηθισμένων διαφορικών εξισώσεων, χρησιμοποιείται συχνά ο συμβολισμός των παραγώγων ως προς τα διαφορικά:

V)
– εξίσωση δεύτερης τάξης.

ΣΟΛ)
– εξίσωση πρώτης τάξης,

γεννήτρια μετά από διαίρεση με dxισοδύναμη μορφή προσδιορισμού της εξίσωσης:
.

Λειτουργία
ονομάζεται λύση μιας συνηθισμένης διαφορικής εξίσωσης εάν, κατά την αντικατάστασή της, μετατρέπεται σε ταυτότητα.

Για παράδειγμα, μια εξίσωση 3ης τάξης

Έχει λύση
.

Η εύρεση με τη μία ή την άλλη μέθοδο, για παράδειγμα, επιλογή, μιας συνάρτησης που ικανοποιεί την εξίσωση δεν σημαίνει και επίλυσή της. Για να λύσετε μια συνηθισμένη διαφορική εξίσωση σημαίνει να βρείτε Ολασυναρτήσεις που σχηματίζουν ταυτότητα όταν αντικαθίστανται σε εξίσωση. Για την εξίσωση (1.1), μια οικογένεια τέτοιων συναρτήσεων σχηματίζεται χρησιμοποιώντας αυθαίρετες σταθερές και ονομάζεται γενική λύση μιας συνηθισμένης διαφορικής εξίσωσης n-η τάξη, και ο αριθμός των σταθερών συμπίπτει με τη σειρά της εξίσωσης: Η γενική λύση μπορεί να είναι, αλλά δεν επιλύεται ρητά σε σχέση με y(Χ) : Στην περίπτωση αυτή, η λύση ονομάζεται συνήθως γενικό ολοκλήρωμα της εξίσωσης (1.1).

Για παράδειγμα, η γενική λύση της διαφορικής εξίσωσης
είναι η ακόλουθη έκφραση: , και ο δεύτερος όρος μπορεί επίσης να γραφτεί ως
, αφού μια αυθαίρετη σταθερά , διαιρούμενο με 2, μπορεί να αντικατασταθεί από μια νέα αυθαίρετη σταθερά .

Εκχωρώντας ορισμένες αποδεκτές τιμές σε όλες τις αυθαίρετες σταθερές στη γενική λύση ή στο γενικό ολοκλήρωμα, λαμβάνουμε μια συγκεκριμένη συνάρτηση που δεν περιέχει πλέον αυθαίρετες σταθερές. Αυτή η συνάρτηση ονομάζεται μερική λύση ή μερικό ολοκλήρωμα της εξίσωσης (1.1). Για την εύρεση των τιμών των αυθαίρετων σταθερών, και επομένως μιας συγκεκριμένης λύσης, χρησιμοποιούνται διάφορες πρόσθετες συνθήκες στην εξίσωση (1.1). Για παράδειγμα, οι λεγόμενες αρχικές συνθήκες μπορούν να καθοριστούν στο (1.2)

Στη δεξιά πλευρά των αρχικών συνθηκών (1.2) καθορίζονται οι αριθμητικές τιμές της συνάρτησης και των παραγώγων και ο συνολικός αριθμός των αρχικών συνθηκών είναι ίσος με τον αριθμό των καθορισμένων αυθαίρετων σταθερών.

Το πρόβλημα της εύρεσης μιας συγκεκριμένης λύσης στην εξίσωση (1.1) με βάση τις αρχικές συνθήκες ονομάζεται πρόβλημα Cauchy.

§ 2. Συνήθεις διαφορικές εξισώσεις 1ης τάξης - βασικές έννοιες.

Συνήθης διαφορική εξίσωση 1ης τάξης ( n=1) έχει τη μορφή:
ή, εάν μπορεί να επιλυθεί σε σχέση με το παράγωγο:
. Κοινή απόφαση y= y(Χ,ΜΕ)ή γενικό ολοκλήρωμα
Οι εξισώσεις 1ης τάξης περιέχουν μια αυθαίρετη σταθερά. Η μόνη αρχική προϋπόθεση για μια εξίσωση 1ης τάξης
σας επιτρέπει να προσδιορίσετε την τιμή μιας σταθεράς από μια γενική λύση ή από ένα γενικό ολοκλήρωμα. Έτσι, θα βρεθεί μια συγκεκριμένη λύση ή, που είναι το ίδιο, θα λυθεί το πρόβλημα Cauchy. Το ζήτημα της ύπαρξης και της μοναδικότητας μιας λύσης στο πρόβλημα Cauchy είναι ένα από τα κεντρικά στη γενική θεωρία των συνηθισμένων διαφορικών εξισώσεων. Για μια εξίσωση 1ης τάξης, ειδικότερα, ισχύει το θεώρημα, το οποίο γίνεται δεκτό εδώ χωρίς απόδειξη.

Θεώρημα 2.1.Αν στην εξίσωση η συνάρτηση
και το μερικό παράγωγό του
συνεχής σε κάποια περιοχή ρεεπίπεδο XOY, και σε αυτήν την περιοχή καθορίζεται ένα σημείο
, τότε υπάρχει μια μοναδική λύση που ικανοποιεί τόσο την εξίσωση όσο και την αρχική συνθήκη
.

Γεωμετρικά, η γενική λύση μιας εξίσωσης 1ης τάξης είναι μια οικογένεια καμπυλών στο επίπεδο XOY, που δεν έχουν κοινά σημεία και διαφέρουν μεταξύ τους σε μία παράμετρο - την τιμή της σταθεράς ντο. Αυτές οι καμπύλες ονομάζονται ολοκληρωμένες καμπύλες για μια δεδομένη εξίσωση. Οι καμπύλες ολοκληρωτικών εξισώσεων έχουν μια προφανή γεωμετρική ιδιότητα: σε κάθε σημείο, η εφαπτομένη της εφαπτομένης στην καμπύλη είναι ίση με την τιμή της δεξιάς πλευράς της εξίσωσης σε αυτό το σημείο:
. Με άλλα λόγια, η εξίσωση δίνεται στο επίπεδο XOYπεδίο των κατευθύνσεων των εφαπτομένων σε ακέραιες καμπύλες. Σχόλιο:Θα πρέπει να σημειωθεί ότι στην εξ.
η εξίσωση και η λεγόμενη εξίσωση δίνονται σε συμμετρική μορφή
.

§ 3. Διαφορικές εξισώσεις 1ης τάξης με διαχωρίσιμες μεταβλητές.

Ορισμός.Μια διαφορική εξίσωση με χωριστές μεταβλητές είναι μια εξίσωση της μορφής
(3.1)

ή μια εξίσωση της μορφής (3.2)

Για να διαχωριστούν οι μεταβλητές της εξίσωσης (3.1), δηλ. μειώστε αυτήν την εξίσωση στη λεγόμενη εξίσωση διαχωρισμένης μεταβλητής, κάντε τα εξής:

;

Τώρα πρέπει να λύσουμε την εξίσωση σολ(y)= 0 . Αν έχει πραγματική λύση y= ένα, Οτι y= έναθα είναι επίσης λύση στην εξίσωση (3.1).

Η εξίσωση (3.2) ανάγεται σε μια διαχωρισμένη μεταβλητή εξίσωση διαιρώντας με το γινόμενο
:

, που μας επιτρέπει να λάβουμε το γενικό ολοκλήρωμα της εξίσωσης (3.2):
. (3.3)

Οι ολοκληρωτικές καμπύλες (3.3) θα συμπληρωθούν με λύσεις
, εάν υπάρχουν τέτοιες λύσεις.

Λύστε την εξίσωση: .

Διαχωρίζουμε τις μεταβλητές:


.

Ενσωματώνοντας, παίρνουμε

Περαιτέρω από τις εξισώσεις
Και
βρίσκουμε Χ=1, y=-1. Αυτές οι λύσεις είναι ιδιωτικές λύσεις.

§ 4. Ομογενείς διαφορικές εξισώσεις 1ης τάξης.

Ορισμός 1.Μια εξίσωση 1ης τάξης ονομάζεται ομοιογενής εάν για τη δεξιά πλευρά της για οποιαδήποτε
ισχύει η αναλογία
, που ονομάζεται συνθήκη ομοιογένειας μιας συνάρτησης δύο μεταβλητών μηδενικής διάστασης.

Παράδειγμα 1.Δείξτε αυτή τη λειτουργία
- ομοιογενής μηδενική διάσταση.

Λύση.

,

Q.E.D.

Θεώρημα.Οποιαδήποτε λειτουργία
- ομοιογενής και, αντιστρόφως, οποιαδήποτε ομοιογενής συνάρτηση
η μηδενική διάσταση μειώνεται στη μορφή
.

Απόδειξη.

Η πρώτη δήλωση του θεωρήματος είναι προφανής, γιατί
. Ας αποδείξουμε τη δεύτερη δήλωση. Ας βάλουμε
, τότε για μια ομοιογενή συνάρτηση
, που ήταν αυτό που έπρεπε να αποδειχθεί.

Ορισμός 2.Εξίσωση (4.1)

στο οποίο ΜΚαι Ν– ομοιογενείς συναρτήσεις ίδιου βαθμού, δηλ. έχουν την ιδιοκτησία για όλους , ονομάζεται ομοιογενής.

Προφανώς, αυτή η εξίσωση μπορεί πάντα να αναχθεί στη μορφή
(4.2), αν και για να το λύσετε δεν χρειάζεται να το κάνετε αυτό.

Μια ομοιογενής εξίσωση ανάγεται σε μια εξίσωση με χωριστές μεταβλητές αντικαθιστώντας την επιθυμητή συνάρτηση yσύμφωνα με τον τύπο y= zx, Οπου z(Χ) – νέα απαιτούμενη λειτουργία. Έχοντας πραγματοποιήσει αυτή την αντικατάσταση στην εξίσωση (4.2), λαμβάνουμε:
ή
ή
.

Ολοκληρώνοντας, λαμβάνουμε το γενικό ολοκλήρωμα της εξίσωσης ως προς τη συνάρτηση z(Χ)
, το οποίο μετά από επανειλημμένη αντικατάσταση
δίνει το γενικό ολοκλήρωμα της αρχικής εξίσωσης. Επιπλέον, εάν - ρίζες της εξίσωσης
, μετά τις συναρτήσεις
- επίλυση ομοιογενούς δεδομένης εξίσωσης. Αν
, τότε η εξίσωση (4.2) παίρνει τη μορφή

και γίνεται εξίσωση με χωριστές μεταβλητές. Οι λύσεις του είναι ημιάμεσες:
.

Σχόλιο.Μερικές φορές συνιστάται η χρήση της αντικατάστασης αντί της παραπάνω αντικατάστασης Χ= zy.

§ 5. Διαφορικές εξισώσεις ανάγονται σε ομοιογενείς.

Θεωρήστε μια εξίσωση της μορφής
. (5.1)

Αν
, τότε αυτή είναι η εξίσωση με χρήση αντικατάστασης, όπου Και - νέες μεταβλητές και - ορισμένοι σταθεροί αριθμοί που προσδιορίζονται από το σύστημα

Ανάγεται σε ομοιογενή εξίσωση

Αν
, τότε η εξίσωση (5.1) παίρνει τη μορφή

.

πιστεύοντας z= τσεκούρι+ με, φτάνουμε σε μια εξίσωση που δεν περιέχει ανεξάρτητη μεταβλητή.

Ας δούμε παραδείγματα.

Παράδειγμα 1.

Ολοκληρώστε την εξίσωση

και επισημάνετε την ολοκληρωτική καμπύλη που διέρχεται από τα σημεία: α) (2;2); β) (1;-1).

Λύση.

Ας βάλουμε y= zx. Επειτα dy= xdz+ zdxΚαι

Ας το συντομεύσουμε και συγκεντρώνουν μέλη στο dxΚαι dz:

Ας διαχωρίσουμε τις μεταβλητές:

.

Ενσωματώνοντας, παίρνουμε ;

ή
,
.

Αντικατάσταση εδώ zεπί , λαμβάνουμε το γενικό ολοκλήρωμα της δεδομένης εξίσωσης με τη μορφή (5.2)
ή

.

Αυτή είναι μια οικογένεια κύκλων
, του οποίου τα κέντρα βρίσκονται στην ευθεία γραμμή y = Χκαι τα οποία στην αρχή εφάπτονται στη γραμμή y + Χ = 0. Αυτή η γραμμήy = - Χ με τη σειρά του, μια συγκεκριμένη λύση της εξίσωσης.

Τώρα ο τρόπος του προβλήματος Cauchy:

Α) βάζοντας στο γενικό ολοκλήρωμα Χ=2, y=2, βρίσκουμε C=2,επομένως η απαιτούμενη λύση θα είναι
.

Β) κανένας από τους κύκλους (5.2) δεν διέρχεται από το σημείο (1;-1). Αλλά είναι ημι-ίσιο y = - Χ,
διέρχεται από το σημείο και δίνει την απαιτούμενη λύση.

Παράδειγμα 2.Λύστε την εξίσωση: .

Λύση.

Η εξίσωση είναι μια ειδική περίπτωση της εξίσωσης (5.1).

Καθοριστικός
σε αυτό το παράδειγμα
, οπότε πρέπει να λύσουμε το παρακάτω σύστημα

Λύνοντας, το καταλαβαίνουμε
. Εκτελώντας μια αντικατάσταση σε μια δεδομένη εξίσωση
, παίρνουμε μια ομοιογενή εξίσωση. Ενσωμάτωσή του με χρήση αντικατάστασης
, βρίσκουμε
.

Επιστροφή στις παλιές μεταβλητές ΧΚαι yσύμφωνα με τους τύπους
, έχουμε .

§ 6. Γενικευμένη ομοιογενής εξίσωση.

Η εξίσωση Μ(Χ, y) dx+ Ν(Χ, y) dy=0 ονομάζεται γενικευμένη ομοιογενής εάν είναι δυνατόν να επιλεγεί ένας τέτοιος αριθμός κ, ότι η αριστερή πλευρά αυτής της εξίσωσης γίνεται ομοιογενής συνάρτηση κάποιου βαθμού Μσχετικά Χ, y, dxΚαι dyυπό την προϋπόθεση ότι Χθεωρείται η τιμή της πρώτης διάστασης, y – κου μετρήσεις , dxΚαι dy – αντίστοιχα μηδέν και (κ-1) ου μετρήσεις. Για παράδειγμα, αυτή θα ήταν η εξίσωση
. (6.1)

Ισχύει σύμφωνα με τις παραδοχές που έγιναν σχετικά με τις μετρήσεις

Χ, y, dxΚαι dyμέλη της αριστερής πλευράς
Και dyθα έχει διαστάσεις -2, 2 αντίστοιχα κΚαι κ-1. Εξισώνοντάς τα, λαμβάνουμε μια συνθήκη που πρέπει να ικανοποιεί ο απαιτούμενος αριθμός κ: -2 = 2κ=κ-1. Αυτή η προϋπόθεση ικανοποιείται όταν κ= -1 (με αυτό κόλοι οι όροι στην αριστερή πλευρά της εξίσωσης που εξετάζουμε θα έχουν διάσταση -2). Κατά συνέπεια, η εξίσωση (6.1) είναι γενικευμένη ομοιογενής.

Η γενικευμένη ομοιογενής εξίσωση ανάγεται σε μια εξίσωση με χωριστές μεταβλητές χρησιμοποιώντας αντικατάσταση
, Οπου z– νέα άγνωστη λειτουργία. Ας ολοκληρώσουμε την εξίσωση (6.1) χρησιμοποιώντας την υποδεικνυόμενη μέθοδο. Επειδή κ= -1, λοιπόν
, μετά την οποία παίρνουμε την εξίσωση .

Ενσωματώνοντάς το, βρίσκουμε
, που
. Αυτή είναι μια γενική λύση της εξίσωσης (6.1).

§ 7. Γραμμικές διαφορικές εξισώσεις 1ης τάξης.

Μια γραμμική εξίσωση 1ης τάξης είναι μια εξίσωση που είναι γραμμική ως προς την επιθυμητή συνάρτηση και την παράγωγό της. Μοιάζει:

, (7.1)

Οπου Π(Χ) Και Q(Χ) – δίνονται συνεχείς συναρτήσεις του Χ. Εάν η συνάρτηση
, τότε η εξίσωση (7.1) έχει τη μορφή:
(7.2)

και ονομάζεται γραμμική ομοιογενής εξίσωση, αλλιώς
ονομάζεται γραμμική ανομοιογενής εξίσωση.

Η γραμμική ομοιογενής διαφορική εξίσωση (7.2) είναι μια εξίσωση με χωριστές μεταβλητές:

(7.3)

Η έκφραση (7.3) είναι η γενική λύση της εξίσωσης (7.2). Να βρεθεί μια γενική λύση της εξίσωσης (7.1), στην οποία η συνάρτηση Π(Χ) δηλώνει την ίδια συνάρτηση με την εξίσωση (7.2), εφαρμόζουμε μια τεχνική που ονομάζεται μέθοδος μεταβολής μιας αυθαίρετης σταθεράς και αποτελείται από τα εξής: θα προσπαθήσουμε να επιλέξουμε τη συνάρτηση C=C(Χ) έτσι ώστε η γενική λύση της γραμμικής ομογενούς εξίσωσης (7.2) να είναι λύση της ανομοιογενούς γραμμικής εξίσωσης (7.1). Τότε για την παράγωγο της συνάρτησης (7.3) λαμβάνουμε:

.

Αντικαθιστώντας την ευρεθείσα παράγωγο στην εξίσωση (7.1), θα έχουμε:

ή
.

Οπου
, όπου είναι μια αυθαίρετη σταθερά. Ως αποτέλεσμα, η γενική λύση στην ανομοιογενή γραμμική εξίσωση (7.1) θα είναι (7.4)

Ο πρώτος όρος σε αυτόν τον τύπο αντιπροσωπεύει τη γενική λύση (7.3) της γραμμικής ομοιογενούς διαφορικής εξίσωσης (7.2) και ο δεύτερος όρος του τύπου (7.4) είναι μια συγκεκριμένη λύση της γραμμικής ανομοιογενούς εξίσωσης (7.1), που προκύπτει από τη γενική ( 7.4) με
. Τονίζουμε αυτό το σημαντικό συμπέρασμα με τη μορφή ενός θεωρήματος.

Θεώρημα.Εάν είναι γνωστή μια συγκεκριμένη λύση μιας γραμμικής ανομοιογενούς διαφορικής εξίσωσης
, τότε όλες οι άλλες λύσεις έχουν τη μορφή
, Οπου
- γενική λύση της αντίστοιχης γραμμικής ομογενούς διαφορικής εξίσωσης.

Ωστόσο, πρέπει να σημειωθεί ότι για την επίλυση της γραμμικής ανομοιογενούς διαφορικής εξίσωσης της 1ης τάξης (7.1), χρησιμοποιείται συχνότερα μια άλλη μέθοδος, που μερικές φορές ονομάζεται μέθοδος Bernoulli. Θα αναζητήσουμε τη λύση της εξίσωσης (7.1) στη μορφή
. Επειτα
. Ας αντικαταστήσουμε την ευρεθείσα παράγωγο στην αρχική εξίσωση:
.

Ας συνδυάσουμε, για παράδειγμα, τον δεύτερο και τον τρίτο όρο της τελευταίας παράστασης και ας εξαγάγουμε τη συνάρτηση u(Χ) πίσω από την αγκύλη:
(7.5)

Απαιτούμε να ακυρωθεί η παρένθεση:
.

Ας λύσουμε αυτήν την εξίσωση θέτοντας μια αυθαίρετη σταθερά ντοίσο με μηδέν:
. Με τη συνάρτηση που βρέθηκε v(Χ) Ας επιστρέψουμε στην εξίσωση (7.5):
.

Λύνοντάς το, παίρνουμε:
.

Επομένως, η γενική λύση της εξίσωσης (7.1) έχει τη μορφή:

§ 8. Εξίσωση Bernoulli.

Ορισμός.

Διαφορική εξίσωση της φόρμας
, Οπου
, ονομάζεται εξίσωση του Bernoulli.

Υποθέτοντας ότι
, διαιρέστε και τις δύο πλευρές της εξίσωσης Bernoulli με . Ως αποτέλεσμα παίρνουμε:
(8.1)

Ας εισαγάγουμε μια νέα λειτουργία
. Επειτα
. Ας πολλαπλασιάσουμε την εξίσωση (8.1) επί
και πάμε στη συνάρτηση z(Χ) :
, δηλ. για λειτουργία z(Χ) έλαβε μια γραμμική ανομοιογενή εξίσωση 1ης τάξης. Αυτή η εξίσωση λύνεται χρησιμοποιώντας τις μεθόδους που συζητήθηκαν στην προηγούμενη παράγραφο. Ας αντικαταστήσουμε τη γενική του λύση z(Χ) έκφραση
, παίρνουμε το γενικό ολοκλήρωμα της εξίσωσης Bernoulli, το οποίο επιλύεται εύκολα σε σχέση με y. Στο
προστίθεται διάλυμα y(Χ)=0 . Η εξίσωση του Bernoulli μπορεί επίσης να λυθεί χωρίς να γίνει η μετάβαση σε μια γραμμική εξίσωση με αντικατάσταση
, και χρησιμοποιώντας τη μέθοδο Bernoulli, που συζητήθηκε λεπτομερώς στο § 7. Ας εξετάσουμε τη χρήση αυτής της μεθόδου για την επίλυση της εξίσωσης Bernoulli χρησιμοποιώντας ένα συγκεκριμένο παράδειγμα.

Παράδειγμα.Βρείτε τη γενική λύση της εξίσωσης:
(8.2)

Λύση.

Επομένως, η γενική λύση αυτής της εξίσωσης έχει τη μορφή:
, y(Χ)=0.

§ 9. Διαφορικές εξισώσεις σε ολικά διαφορικά.

Ορισμός.Αν στην Εξ. Μ(Χ, y) dx+ Ν(Χ, y) dy=0 (9.1) η αριστερή πλευρά είναι το συνολικό διαφορικό κάποιας συνάρτησης U(Χ, y) , τότε ονομάζεται ολική διαφορική εξίσωση. Αυτή η εξίσωση μπορεί να ξαναγραφτεί ως du(Χ, y)=0 , επομένως, το γενικό του ολοκλήρωμα είναι u(Χ, y)= ντο.

Για παράδειγμα, η εξίσωση xdy+ Υδξ=0 υπάρχει μια εξίσωση στα συνολικά διαφορικά, αφού μπορεί να ξαναγραφτεί στη μορφή ρε(xy)=0. Το γενικό ολοκλήρωμα θα είναι xy= ντο- αυθαίρετη διαφοροποιήσιμη συνάρτηση. Ας διαφοροποιήσουμε το (9.3) σε σχέση με το u
§ 10. Συντελεστής ολοκλήρωσης.

Αν η εξίσωση Μ(Χ, y) dx + Ν(Χ, y) dy = 0 δεν είναι συνολική διαφορική εξίσωση και υπάρχει συνάρτηση µ = µ(Χ, y) , έτσι ώστε αφού πολλαπλασιάσουμε και τις δύο πλευρές της εξίσωσης με αυτό, να προκύψει η εξίσωση

μ(Mdx + Ndy) = 0στα συνολικά διαφορικά, δηλ. μ(Mdx + Ndy)du, μετά η συνάρτηση µ(Χ, y) ονομάζεται συντελεστής ολοκλήρωσης της εξίσωσης. Στην περίπτωση που η εξίσωση είναι ήδη μια εξίσωση σε ολικά διαφορικά, υποθέτουμε μ = 1.

Εάν βρεθεί ο συντελεστής ολοκλήρωσης µ , τότε η ολοκλήρωση αυτής της εξίσωσης ανάγεται στον πολλαπλασιασμό και των δύο πλευρών της επί µ και εύρεση του γενικού ολοκληρώματος της εξίσωσης που προκύπτει σε ολικά διαφορικά.

Αν µ είναι μια συνεχώς διαφοροποιήσιμη συνάρτηση του ΧΚαι y, Οτι
.

Από αυτό προκύπτει ότι ο παράγοντας ολοκλήρωσης µ ικανοποιεί την ακόλουθη μερική διαφορική εξίσωση 1ης τάξης:

(10.1).

Αν είναι εκ των προτέρων γνωστό ότι µ= µ(ω) , Οπου ω – δεδομένη συνάρτηση από ΧΚαι y, τότε η εξίσωση (10.1) ανάγεται σε μια συνηθισμένη (και, επιπλέον, γραμμική) εξίσωση με άγνωστη συνάρτηση µ σε ανεξάρτητη μεταβλητή ω :

(10.2),

Οπου
, δηλαδή το κλάσμα είναι συνάρτηση μόνο του ω .

Επιλύοντας την εξίσωση (10.2), βρίσκουμε τον συντελεστή ολοκλήρωσης

, Με = 1.

Ειδικότερα, η εξίσωση Μ(Χ, y) dx + Ν(Χ, y) dy = 0 έχει έναν παράγοντα ολοκλήρωσης που εξαρτάται μόνο από Χ(ω = Χ) ή μόνο από y(ω = y), εάν πληρούνται αναλόγως οι ακόλουθες προϋποθέσεις:

,

,
.

Κάνοντας κλικ στο κουμπί «Λήψη αρχείου», θα κατεβάσετε το αρχείο που χρειάζεστε εντελώς δωρεάν.
Προτού κατεβάσετε αυτό το αρχείο, σκεφτείτε εκείνα τα καλά δοκίμια, τεστ, εργασίες όρου, διατριβές, άρθρα και άλλα έγγραφα που βρίσκονται αζήτητα στον υπολογιστή σας. Αυτή είναι η δουλειά σας, θα πρέπει να συμμετέχει στην ανάπτυξη της κοινωνίας και να ωφελεί τους ανθρώπους. Βρείτε αυτά τα έργα και υποβάλετέ τα στη βάση γνώσεων.
Εμείς και όλοι οι φοιτητές, μεταπτυχιακοί φοιτητές, νέοι επιστήμονες που χρησιμοποιούν τη βάση γνώσεων στις σπουδές και την εργασία τους θα σας είμαστε πολύ ευγνώμονες.

Για λήψη ενός αρχείου με ένα έγγραφο, εισαγάγετε έναν πενταψήφιο αριθμό στο παρακάτω πεδίο και κάντε κλικ στο κουμπί "Λήψη αρχείου"

Παρόμοια έγγραφα

    Προβλήματα Cauchy για διαφορικές εξισώσεις. Γράφημα της λύσης μιας διαφορικής εξίσωσης πρώτης τάξης. Εξισώσεις με χωριστές μεταβλητές και αναγωγή σε ομοιογενή εξίσωση. Ομογενείς και ανομοιογενείς γραμμικές εξισώσεις πρώτης τάξης. εξίσωση Bernoulli.

    διάλεξη, προστέθηκε 18/08/2012

    Βασικές έννοιες της θεωρίας των συνηθισμένων διαφορικών εξισώσεων. Πρόσημο εξίσωσης σε ολικά διαφορικά, κατασκευή γενικού ολοκληρώματος. Οι απλούστερες περιπτώσεις εύρεσης του συντελεστή ολοκλήρωσης. Η περίπτωση ενός πολλαπλασιαστή που εξαρτάται μόνο από το X και μόνο από το Y.

    εργασία μαθήματος, προστέθηκε 24/12/2014

    Χαρακτηριστικά των διαφορικών εξισώσεων ως σχέσεις μεταξύ συναρτήσεων και παραγώγων τους. Απόδειξη του θεωρήματος ύπαρξης και μοναδικότητας της λύσης. Παραδείγματα και αλγόριθμος επίλυσης εξισώσεων σε ολικά διαφορικά. Συντελεστής ολοκλήρωσης σε παραδείγματα.

    εργασία μαθήματος, προστέθηκε 02/11/2014

    Διαφορικές εξισώσεις Riccati. Γενική λύση γραμμικής εξίσωσης. Εύρεση όλων των πιθανών λύσεων στη διαφορική εξίσωση του Bernoulli. Επίλυση εξισώσεων με χωριστές μεταβλητές. Γενικές και ειδικές λύσεις της διαφορικής εξίσωσης Clairaut.

    εργασία μαθήματος, προστέθηκε 26/01/2015

    Εξίσωση με διαχωρίσιμες μεταβλητές. Ομογενείς και γραμμικές διαφορικές εξισώσεις. Γεωμετρικές ιδιότητες ολοκληρωτικών καμπυλών. Πλήρες διαφορικό συνάρτησης δύο μεταβλητών. Προσδιορισμός του ολοκληρώματος με μεθόδους Bernoulli και μεταβολές μιας αυθαίρετης σταθεράς.

    περίληψη, προστέθηκε 24/08/2015

    Έννοιες και λύσεις των απλούστερων διαφορικών εξισώσεων και διαφορικών εξισώσεων αυθαίρετης τάξης, συμπεριλαμβανομένων εκείνων με σταθερούς αναλυτικούς συντελεστές. Συστήματα γραμμικών εξισώσεων. Ασυμπτωτική συμπεριφορά λύσεων ορισμένων γραμμικών συστημάτων.

    διατριβή, προστέθηκε 06/10/2010

    Γενικό ολοκλήρωμα εξίσωσης, εφαρμογή της μεθόδου Lagrange για την επίλυση ανομοιογενούς γραμμικής εξίσωσης με άγνωστη συνάρτηση. Επίλυση διαφορικής εξίσωσης σε παραμετρική μορφή. Συνθήκη Euler, εξίσωση πρώτης τάξης σε ολικά διαφορικά.

    δοκιμή, προστέθηκε στις 11/02/2011