Χρησιμοποιώντας την αριθμομηχανή

Για να αξιολογήσετε μια έκφραση, πρέπει να εισαγάγετε μια συμβολοσειρά για αξιολόγηση. Κατά την εισαγωγή αριθμών, το διαχωριστικό μεταξύ του ακέραιου και του κλασματικού μέρους είναι μια τελεία. Μπορείτε να χρησιμοποιήσετε παρενθέσεις. Πράξεις σε μιγαδικούς αριθμούς είναι ο πολλαπλασιασμός (*), η διαίρεση (/), η πρόσθεση (+), η αφαίρεση (-), η εκτίμηση (^) και άλλες. Μπορείτε να χρησιμοποιήσετε εκθετικές και αλγεβρικές μορφές για να γράψετε μιγαδικούς αριθμούς. Εισαγάγετε τη φανταστική μονάδα Εγώείναι δυνατό χωρίς το σύμβολο του πολλαπλασιασμού σε άλλες περιπτώσεις, το πρόσημο πολλαπλασιασμού απαιτείται, για παράδειγμα, μεταξύ παρενθέσεων ή μεταξύ ενός αριθμού και μιας σταθεράς. Μπορούν επίσης να χρησιμοποιηθούν σταθερές: ο αριθμός π εισάγεται ως pi, εκθέτης μι, οποιεσδήποτε εκφράσεις στην ένδειξη πρέπει να περιβάλλονται από παρενθέσεις.

Παράδειγμα γραμμής υπολογισμού: (4,5+i12)*(3,2i-2,5)/e^(i1,25*pi), που αντιστοιχεί στην έκφραση \[\frac((4(,)5 + i12)(3(,)2i-2(,)5))(e^(i1(,)25\pi))\]

Η αριθμομηχανή μπορεί να χρησιμοποιεί σταθερές, μαθηματικές συναρτήσεις, πρόσθετες πράξεις και πιο σύνθετες εκφράσεις, μπορείτε να εξοικειωθείτε με αυτές τις δυνατότητες στη σελίδα των γενικών κανόνων για τη χρήση αριθμομηχανών σε αυτόν τον ιστότοπο.

Ο ιστότοπος είναι υπό κατασκευή, ορισμένες σελίδες ενδέχεται να μην είναι διαθέσιμες.

Νέα

07.07.2016
Προστέθηκε αριθμομηχανή για την επίλυση συστημάτων μη γραμμικών αλγεβρικών εξισώσεων: .

30.06.2016
Ο ιστότοπος έχει αποκριτικό σχεδιασμό, οι σελίδες εμφανίζονται επαρκώς τόσο σε μεγάλες οθόνες όσο και σε κινητές συσκευές.

Ανάδοχος

RGRONline.ru – άμεση λύση για ηλεκτρολογικές εργασίες στο διαδίκτυο.

Τάξη 12 . Μιγαδικοί αριθμοί.

12.1. Ορισμός μιγαδικών αριθμών σε αλγεβρική μορφή. Σύγκριση και αναπαράσταση μιγαδικών αριθμών στο μιγαδικό επίπεδο. Σύνθετη σύζευξη. Πρόσθεση, πολλαπλασιασμός, διαίρεση μιγαδικών αριθμών.

12.2. Συντελεστής, όρισμα μιγαδικού αριθμού.

12.3. Τριγωνομετρικές και εκθετικές μορφές γραφής μιγαδικού αριθμού.

12.4. Αύξηση σε ακέραιο αριθμό και εξαγωγή της ρίζας ενός μιγαδικού αριθμού.

Ορισμός μιγαδικών αριθμών σε αλγεβρική μορφή. Σύγκριση και αναπαράσταση μιγαδικών αριθμών στο μιγαδικό επίπεδο. Σύνθετη σύζευξη. Πρόσθεση, πολλαπλασιασμός, διαίρεση μιγαδικών αριθμών.

Ένας μιγαδικός αριθμός σε αλγεβρική μορφή είναι ο αριθμός

Οπου
που ονομάζεται φανταστική μονάδαΚαι
- πραγματικοί αριθμοί:
που ονομάζεται πραγματικό (πραγματικό) μέρος;
- φανταστικό μέροςμιγαδικός αριθμός . Μιγαδικοί αριθμοί της φόρμας
λέγονται καθαρά φανταστικούς αριθμούς. Το σύνολο όλων των μιγαδικών αριθμών συμβολίζεται με το γράμμα .

Α-προπατορικό,

Το σύνολο όλων των πραγματικών αριθμών είναι μέρος του σετ
: . Από την άλλη, υπάρχουν μιγαδικοί αριθμοί που δεν ανήκουν στο σύνολο . Για παράδειγμα,
Και
, επειδή
.

Οι μιγαδικοί αριθμοί σε αλγεβρική μορφή προκύπτουν φυσικά κατά την επίλυση τετραγωνικών εξισώσεων με αρνητική διάκριση.

Παράδειγμα 1. Λύστε την εξίσωση
.

Λύση. ,

Επομένως, η δεδομένη τετραγωνική εξίσωση έχει σύνθετες ρίζες

,
.

Παράδειγμα 2. Βρείτε τα πραγματικά και τα φανταστικά μέρη των μιγαδικών αριθμών

,

,
.

Αντίστοιχα, τα πραγματικά και τα φανταστικά μέρη του αριθμού ,

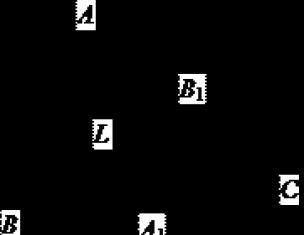
Οποιοσδήποτε μιγαδικός αριθμός
που αντιπροσωπεύεται από ένα διάνυσμα στο μιγαδικό επίπεδο , που αντιπροσωπεύει ένα επίπεδο με καρτεσιανό σύστημα συντεταγμένων
. Η αρχή του διανύσματος βρίσκεται στο σημείο , και το τέλος είναι στο σημείο με συντεταγμένες
(Εικόνα 1.) Άξονας
ονομάζεται πραγματικός άξονας, και ο άξονας
- νοητός άξονας του μιγαδικού επιπέδου .

Οι μιγαδικοί αριθμοί συγκρίνονται μεταξύ τους μόνο με πρόσημα
. . Εάν τουλάχιστον μία από τις ισότητες:
παραβιάζεται λοιπόν
. Εγγραφές τύπου
δεν έχει νόημα.

Εξ ορισμού, σύνθετο αριθμός
ονομάζεται το μιγαδικό συζυγές ενός αριθμού
. Σε αυτή την περίπτωση γράφουν
. Είναι προφανές ότι
. Παντού κάτω, μια υπερμπάρα πάνω από έναν μιγαδικό αριθμό θα σημαίνει σύνθετη σύζευξη.

Για παράδειγμα, .

Μπορείτε να εκτελέσετε πράξεις σε μιγαδικούς αριθμούς όπως πρόσθεση (αφαίρεση), πολλαπλασιασμό και διαίρεση.

1. Πρόσθεση μιγαδικών αριθμώνγίνεται ως εξής:

Ιδιότητες της πράξης προσθήκης:

- ιδιότητα ανταλλαγής.

- ιδιοκτησία της συνειρμικότητας.

Είναι εύκολο να δούμε ότι γεωμετρικά η πρόσθεση μιγαδικών αριθμών
σημαίνει την προσθήκη εκείνων που τους αντιστοιχούν στο αεροπλάνο διανύσματα σύμφωνα με τον κανόνα του παραλληλογράμμου.

Λειτουργία αφαίρεσης αριθμών από τον αριθμό γίνεται ως εξής:

2. Πολλαπλασιασμός μιγαδικών αριθμώνγίνεται ως εξής:

Ιδιότητες της πράξης πολλαπλασιασμού:

- ιδιότητα ανταλλαγής.

- ιδιοκτησία της συνειρμικότητας.

- ο νόμος της κατανομής.

3. Διαίρεση μιγαδικών αριθμών εφικτό μόνο με
και γίνεται ως εξής:

.

Παράδειγμα 3. Εύρημα
, Αν .

Παράδειγμα 4. Υπολογίζω
, Αν .

z, επειδή
.

.(Ωχ!)

Δεν είναι δύσκολο να ελέγξετε (προτείνεται να το κάνετε μόνοι σας) την εγκυρότητα των παρακάτω δηλώσεων:

Συντελεστής, όρισμα μιγαδικού αριθμού.

Μέτρο ενός μιγαδικού αριθμού
(μονάδα μέτρησης συμβολίζεται με ) είναι ένας μη αρνητικός αριθμός
, δηλ.
.

Γεωμετρική σημασία - μήκος του διανύσματος που αντιπροσωπεύει τον αριθμό στο σύνθετο επίπεδο . Η εξίσωση
ορίζει το σύνολο όλων των αριθμών (διανύσματα ανά ), του οποίου τα άκρα βρίσκονται στον μοναδιαίο κύκλο
.

Επιχείρημα μιγαδικού αριθμού
(διαφωνία συμβολίζεται με
) αυτή είναι μια γωνία σε ακτίνια μεταξύ του πραγματικού άξονα
και αριθμός στο σύνθετο επίπεδο , και θετικό εάν υπολογίζεται από
πριν αριστερόστροφα, και αρνητικό εάν μετρηθεί από τον άξονα
πριν δεξιόστροφος.

Άρα το επιχείρημα του αριθμού καθορίζεται διφορούμενα, μέχρι έναν όρο
, Οπου
. Σίγουρα ένα επιχείρημα αριθμών καθορίζεται εντός ενός γύρου του κύκλου μονάδας
στην επιφάνεια . Συνήθως πρέπει να βρείτε
εντός του διαστήματος
,αυτή η τιμή ονομάζεται κύρια τιμή του ορίσματος αριθμού και ορίζεται
.

Και
αριθμοί μπορεί να βρεθεί από την εξίσωση
, όπου Αναγκαίως πρέπει να ληφθούν υπόψη, σε ποιο τέταρτο του αεροπλάνου βρίσκεται το τέλος του διανύσματος - τελεία
:

Αν
(1ο τέταρτο του αεροπλάνου ), Οτι ;

Αν
(2ο τέταρτο του αεροπλάνου ), Οτι;

Αν
(3ο τέταρτο του αεροπλάνου ), Οτι ;

Αν
(4ο τέταρτο του αεροπλάνου ), Οτι .

Στην πραγματικότητα, ο συντελεστής και το όρισμα του αριθμού
, αυτές είναι πολικές συντεταγμένες
σημεία
- τέλος του διανύσματος στην επιφάνεια .

Παράδειγμα 5. Βρείτε το μέτρο και την κύρια τιμή του ορίσματος των αριθμών:

.

Επιχειρήματα αριθμών που βρίσκονται σε άξονες
, που χωρίζει τα τέταρτα 1,2,3,4 του μιγαδικού επιπέδου , μπορεί να βρεθεί αμέσως από τις γραφικές αναπαραστάσεις αυτών των αριθμών στο επίπεδο .

Τριγωνομετρικές και εκθετικές μορφές γραφής μιγαδικού αριθμού. Πολλαπλασιασμός και διαίρεση μιγαδικών αριθμών σε τριγωνομετρικό και εκθετικό συμβολισμό.

Τριγωνομετρική σημειογραφίαμιγαδικός αριθμός
έχει τη μορφή:

, (2)

Οπου - ενότητα, - όρισμα μιγαδικού αριθμού . Αυτή η αναπαράσταση μιγαδικών αριθμών προκύπτει από τις ισότητες.

Εκδηλωτικός(εκθετικός) μορφή γραφής μιγαδικού αριθμού
έχει τη μορφή:

, (3)

Οπου - ενότητα, - επιχείρημα αριθμού . Η δυνατότητα αναπαράστασης μιγαδικών αριθμών σε εκθετική μορφή (3) προκύπτει από την τριγωνομετρική μορφή (2) και τον τύπο του Euler:

. (4)

Αυτός ο τύπος αποδεικνύεται στο μάθημα του TFKP (Θεωρία των συναρτήσεων μιας μιγαδικής μεταβλητής).

Παράδειγμα 6. Βρείτε τριγωνομετρικές και εκθετικές μορφές για μιγαδικούς αριθμούς: από το παράδειγμα 5.

Λύση. Ας χρησιμοποιήσουμε τα αποτελέσματα του Παραδείγματος 5, στο οποίο βρίσκονται οι μονάδες και τα ορίσματα όλων των καθορισμένων αριθμών.

,

.

- τριγωνομετρική μορφή γραφής αριθμού ,

- εκθετική μορφή γραφής αριθμού .

3)

- τριγωνομετρική μορφή γραφής αριθμού ,

- εκθετική μορφή γραφής αριθμού .

Τριγωνομετρική μορφή γραφής αριθμού ,

- εκθετική μορφή γραφής αριθμού .

5)

- τριγωνομετρική μορφή γραφής αριθμού ,

- εκθετική μορφή γραφής αριθμού .

Τριγωνομετρική μορφή αριθμού ,

.

7)

- τριγωνομετρική μορφή γραφής αριθμού ,

- εκθετική μορφή αριθμού .

- τριγωνομετρική μορφή γραφής αριθμού ,

- εκθετική μορφή γραφής αριθμού .

Η εκθετική μορφή γραφής μιγαδικών αριθμών οδηγεί στην ακόλουθη γεωμετρική ερμηνεία των πράξεων πολλαπλασιασμού και διαίρεσης μιγαδικών αριθμών. Αφήνω
- εκθετικές μορφές αριθμών
.

1. Κατά τον πολλαπλασιασμό μιγαδικών αριθμών, οι ενότητες τους πολλαπλασιάζονται και προστίθενται τα ορίσματά τους.

2. Κατά τη διαίρεση ενός μιγαδικού αριθμού ανά αριθμό αποδεικνύεται σύνθετος αριθμός , ενότητα που ισούται με την αναλογία των ενοτήτων , και το επιχείρημα - διαφορές
αριθμητικά επιχειρήματα
.

Αύξηση σε ακέραιο αριθμό και εξαγωγή της ρίζας ενός μιγαδικού αριθμού.

Α-προπατορικό,

Όταν ανυψωθεί σε μια ολόκληρη δύναμη μιγαδικός αριθμός
, θα πρέπει να προχωρήσετε ως εξής: πρώτα βρείτε τη μονάδα και επιχείρημα αυτός ο αριθμός; παρουσιάζω σε παραστατική μορφή
; εύρημα
εκτελώντας την ακόλουθη σειρά ενεργειών

Οπου . (5)

Σχόλιο.Διαφωνία
αριθμοί
μπορεί να μην ανήκει στο διάστημα
. Σε αυτή την περίπτωση, σύμφωνα με την λαμβανόμενη τιμή βρείτε το κύριο νόημα διαφωνία

αριθμοί
, προσθέτοντας (ή αφαιρώντας) έναν αριθμό
με αυτή τη σημασία
, προς την

ανήκε στο μεσοδιάστημα
. Μετά από αυτό, πρέπει να αντικαταστήσετε στους τύπους (5) επί .

Παράδειγμα 7. Εύρημα Και
, Αν
.

1)
=
(βλέπε αριθμό από το παράδειγμα 6).

2)
, Οπου
.
.
.

Ως εκ τούτου, μπορεί να αντικατασταθεί από και, που σημαίνει

Οπου
.

3)
, Οπου
.
.

Θα αντικαταστήσουμε επί . Ως εκ τούτου,

Εξαγωγή ριζών ου βαθμού
από έναν μιγαδικό αριθμό
πραγματοποιείται σύμφωνα με τον τύπο Moivre-Laplace

Μιγαδικοί αριθμοί

Φανταστικο Και μιγαδικοί αριθμοί. τετμημένη και τεταγμένη

μιγαδικός αριθμός. Σύζευξη μιγαδικών αριθμών.

Πράξεις με μιγαδικούς αριθμούς. Γεωμετρικός

αναπαράσταση μιγαδικών αριθμών. Σύνθετο αεροπλάνο.

Συντελεστής και όρισμα μιγαδικού αριθμού. Τριγωνομετρικό

μορφή μιγαδικού αριθμού. Λειτουργίες με σύνθετο

αριθμοί σε τριγωνομετρική μορφή. Η φόρμουλα του Moivre.

Βασικές πληροφορίες για φανταστικο Και μιγαδικοί αριθμοί δίνονται στην ενότητα «Φανταστικοί και μιγαδικοί αριθμοί». Η ανάγκη για αυτούς τους αριθμούς νέου τύπου προέκυψε κατά την επίλυση τετραγωνικών εξισώσεων για την περίπτωσηρε< 0 (здесь ρε– διάκριση τετραγωνικής εξίσωσης). Για πολύ καιρό, αυτοί οι αριθμοί δεν έβρισκαν φυσική εφαρμογή, γι' αυτό και ονομάζονταν «φανταστικοί» αριθμοί. Ωστόσο, τώρα χρησιμοποιούνται πολύ ευρέως σε διάφορους τομείς της φυσικής

και τεχνολογία: ηλεκτρολογική μηχανική, υδρο- και αεροδυναμική, θεωρία ελαστικότητας κ.λπ.

Μιγαδικοί αριθμοί γράφονται με τη μορφή:a+bi. Εδώ έναΚαι σι – πραγματικούς αριθμούς , ΕΝΑ Εγώ – φανταστική μονάδα, δηλ.μι. Εγώ 2 = –1. Αριθμός έναπου ονομάζεται τετμημένη, ένα β – τεταγμένημιγαδικός αριθμόςα + δι.Δύο μιγαδικοί αριθμοίa+biΚαι a–bi λέγονται κλίνωμιγαδικοί αριθμοί.

Βασικές συμφωνίες:

1. Πραγματικός αριθμόςΕΝΑμπορεί επίσης να γραφτεί στη φόρμαμιγαδικός αριθμός:ένα + 0 Εγώή ένα - 0 Εγώ. Για παράδειγμα, εγγραφές 5 + 0Εγώκαι 5-0 Εγώσημαίνει τον ίδιο αριθμό 5 .

2. Μιγαδικός αριθμός 0 + διπου ονομάζεται καθαρά φανταστικό αριθμός. Ρεκόρδισημαίνει το ίδιο με το 0 + δι.

3. Δύο μιγαδικοί αριθμοίa+bi Καιγ + διθεωρούνται ίσα ανα = γΚαι b = d. Σε διαφορετική περίπτωση οι μιγαδικοί αριθμοί δεν είναι ίσοι.

Πρόσθεση. Άθροισμα μιγαδικών αριθμώνa+biΚαι γ + διονομάζεται μιγαδικός αριθμός (α+γ ) + (β+δ ) Εγώ.Ετσι, κατά την προσθήκη οι μιγαδικοί αριθμοί, τα τετμημένα και οι τεταγμένες τους προστίθενται χωριστά.

Αυτός ο ορισμός αντιστοιχεί στους κανόνες για πράξεις με συνηθισμένα πολυώνυμα.

Αφαίρεση. Η διαφορά δύο μιγαδικών αριθμώνa+bi(μειώθηκε) και γ + δι(υπόδρομος) ονομάζεται μιγαδικός αριθμός (μετα Χριστον ) + (β–δ ) Εγώ.

Ετσι, Κατά την αφαίρεση δύο μιγαδικών αριθμών, τα τετμημένα και οι τεταγμένες τους αφαιρούνται χωριστά.

Πολλαπλασιασμός. Γινόμενο μιγαδικών αριθμώνa+biΚαι γ + δι ονομάζεται μιγαδικός αριθμός:

(ac–bd ) + (ad+bc ) Εγώ.Αυτός ο ορισμός προκύπτει από δύο απαιτήσεις:

1) αριθμοί a+biΚαι γ + διπρέπει να πολλαπλασιάζονται σαν αλγεβρικάδιώνυμα,

2) αριθμός Εγώέχει την κύρια ιδιοκτησία:Εγώ 2 = – 1.

ΠΑΡΑΔΕΙΓΜΑ ( α+ δι )(a–bi) = α 2 +β 2 . Ως εκ τούτου, δουλειά

δύο συζευγμένοι μιγαδικοί αριθμοί είναι ίσος με τον πραγματικό

θετικό νούμερο.

Διαίρεση. Διαιρέστε έναν μιγαδικό αριθμόa+bi (διαιρείται) με άλλονγ + δι(διαιρών) - σημαίνει να βρεις τον τρίτο αριθμόe + f i(συνομιλία), η οποία όταν πολλαπλασιάζεται με διαιρέτηγ + δι, έχει ως αποτέλεσμα το μέρισμαα + δι.

Εάν ο διαιρέτης δεν είναι μηδέν, η διαίρεση είναι πάντα δυνατή.

ΠΑΡΑΔΕΙΓΜΑ Εύρεση (8 +Εγώ ) : (2 – 3 Εγώ) .

Λύση Ας ξαναγράψουμε αυτόν τον λόγο ως κλάσμα:

Πολλαπλασιάζοντας τον αριθμητή και τον παρονομαστή του με 2 + 3Εγώ

ΚΑΙ Έχοντας πραγματοποιήσει όλους τους μετασχηματισμούς, παίρνουμε:

Γεωμετρική αναπαράσταση μιγαδικών αριθμών. Οι πραγματικοί αριθμοί αντιπροσωπεύονται από σημεία στην αριθμητική γραμμή:

Εδώ είναι η ουσία ΕΝΑσημαίνει τον αριθμό –3, τελείασι– αριθμός 2, και Ο- μηδέν. Αντίθετα, οι μιγαδικοί αριθμοί αντιπροσωπεύονται από σημεία στο επίπεδο συντεταγμένων. Για το σκοπό αυτό επιλέγουμε ορθογώνιες (καρτεσιανές) συντεταγμένες με τις ίδιες κλίμακες και στους δύο άξονες. Στη συνέχεια ο μιγαδικός αριθμόςa+bi θα παριστάνεται με μια τελεία Π με τετμημένη α και τεταγμένη β (βλέπε εικόνα). Αυτό το σύστημα συντεταγμένων ονομάζεται σύνθετο επίπεδο .

Μονάδα μέτρησης μιγαδικός αριθμός είναι το μήκος του διανύσματοςΕΠ, που αντιπροσωπεύει έναν μιγαδικό αριθμό στη συντεταγμένη ( περιεκτικός) αεροπλάνο. Μέτρο ενός μιγαδικού αριθμούa+biσυμβολίζεται | a+bi| ή επιστολή r

Για να λύσετε προβλήματα με μιγαδικούς αριθμούς, πρέπει να κατανοήσετε τους βασικούς ορισμούς. Ο κύριος στόχος αυτού του άρθρου ανασκόπησης είναι να εξηγήσει τι είναι οι μιγαδικοί αριθμοί και να παρουσιάσει μεθόδους για την επίλυση βασικών προβλημάτων με μιγαδικούς αριθμούς. Έτσι, ένας μιγαδικός αριθμός θα ονομάζεται αριθμός της φόρμας z = a + bi, Οπου α, β- πραγματικοί αριθμοί, οι οποίοι ονομάζονται τα πραγματικά και φανταστικά μέρη ενός μιγαδικού αριθμού, αντίστοιχα, και δηλώνουν a = Re(z), b=Im(z).
Εγώονομάζεται η φανταστική μονάδα. i 2 = -1. Συγκεκριμένα, οποιοσδήποτε πραγματικός αριθμός μπορεί να θεωρηθεί σύνθετος: a = a + 0i, όπου το α είναι πραγματικό. Αν a = 0Και b ≠ 0, τότε ο αριθμός συνήθως ονομάζεται καθαρά φανταστικός.

Τώρα ας εισαγάγουμε πράξεις σε μιγαδικούς αριθμούς.
Θεωρήστε δύο μιγαδικούς αριθμούς z 1 = a 1 + b 1 iΚαι z 2 = a 2 + b 2 i.

Ας σκεφτούμε z = a + bi.

Το σύνολο των μιγαδικών αριθμών επεκτείνει το σύνολο των πραγματικών αριθμών, το οποίο με τη σειρά του επεκτείνει το σύνολο των ρητών αριθμών κ.λπ. Αυτή η αλυσίδα επενδύσεων φαίνεται στο σχήμα: N – φυσικοί αριθμοί, Z – ακέραιοι, Q – ορθολογικοί, R – πραγματικοί, C – μιγαδικοί.

Αναπαράσταση μιγαδικών αριθμών

Αλγεβρική σημειογραφία.

Θεωρήστε έναν μιγαδικό αριθμό z = a + bi, αυτή η μορφή γραφής ενός μιγαδικού αριθμού ονομάζεται αλγεβρικός. Έχουμε ήδη συζητήσει λεπτομερώς αυτήν τη μορφή εγγραφής στην προηγούμενη ενότητα. Το παρακάτω οπτικό σχέδιο χρησιμοποιείται αρκετά συχνά

Τριγωνομετρική μορφή.

Από το σχήμα φαίνεται ότι ο αριθμός z = a + biμπορεί να γραφτεί διαφορετικά. Είναι προφανές ότι a = rcos(φ), b = rsin(φ), r=|z|, ως εκ τούτου z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π) ονομάζεται όρισμα ενός μιγαδικού αριθμού. Αυτή η αναπαράσταση ενός μιγαδικού αριθμού ονομάζεται τριγωνομετρική μορφή. Η τριγωνομετρική μορφή σημειογραφίας είναι μερικές φορές πολύ βολική. Για παράδειγμα, είναι βολικό να το χρησιμοποιήσετε για να αυξήσετε έναν μιγαδικό αριθμό σε μια ακέραια δύναμη, δηλαδή, εάν z = rcos(φ) + rsin(φ)i, Οτι z n = r n cos(nφ) + r n sin(nφ)i, αυτός ο τύπος ονομάζεται Η φόρμουλα του Moivre.

Επιδεικτική μορφή.

Ας σκεφτούμε z = rcos(φ) + rsin(φ)i- έναν μιγαδικό αριθμό σε τριγωνομετρική μορφή, γράψτε τον με άλλη μορφή z = r(cos(φ) + sin(φ)i) = re iφ, η τελευταία ισότητα προκύπτει από τον τύπο του Euler, έτσι έχουμε αποκτήσει μια νέα μορφή γραφής ενός μιγαδικού αριθμού: z = reiφ, η οποία ονομάζεται ενδεικτικός. Αυτή η μορφή σημειογραφίας είναι επίσης πολύ βολική για την αύξηση ενός μιγαδικού αριθμού σε μια δύναμη: z n = r n e inφ, Εδώ nόχι απαραίτητα ακέραιος, αλλά μπορεί να είναι ένας αυθαίρετος πραγματικός αριθμός. Αυτή η μορφή σημειογραφίας χρησιμοποιείται αρκετά συχνά για την επίλυση προβλημάτων.

Θεμελιώδες θεώρημα ανώτερης άλγεβρας

Ας φανταστούμε ότι έχουμε μια τετραγωνική εξίσωση x 2 + x + 1 = 0. Προφανώς, η διάκριση αυτής της εξίσωσης είναι αρνητική και δεν έχει πραγματικές ρίζες, αλλά αποδεικνύεται ότι αυτή η εξίσωση έχει δύο διαφορετικές μιγαδικές ρίζες. Έτσι, το θεμελιώδες θεώρημα της ανώτερης άλγεβρας δηλώνει ότι οποιοδήποτε πολυώνυμο βαθμού n έχει τουλάχιστον μία σύνθετη ρίζα. Από αυτό προκύπτει ότι οποιοδήποτε πολυώνυμο βαθμού n έχει ακριβώς n μιγαδικές ρίζες, λαμβάνοντας υπόψη την πολλαπλότητά τους. Αυτό το θεώρημα είναι ένα πολύ σημαντικό αποτέλεσμα στα μαθηματικά και χρησιμοποιείται ευρέως. Ένα απλό συμπέρασμα αυτού του θεωρήματος είναι ότι υπάρχουν ακριβώς n διαφορετικές ρίζες του βαθμού n της ενότητας.

Κύριοι τύποι εργασιών

Αυτή η ενότητα θα εξετάσει τους κύριους τύπους απλών προβλημάτων που περιλαμβάνουν μιγαδικούς αριθμούς. Συμβατικά, τα προβλήματα που αφορούν μιγαδικούς αριθμούς μπορούν να χωριστούν στις ακόλουθες κατηγορίες.

• Εκτέλεση απλών αριθμητικών πράξεων σε μιγαδικούς αριθμούς.
• Εύρεση των ριζών πολυωνύμων σε μιγαδικούς αριθμούς.
• Αύξηση μιγαδικών αριθμών σε δυνάμεις.
• Εξαγωγή ριζών από μιγαδικούς αριθμούς.
• Χρήση μιγαδικών αριθμών για την επίλυση άλλων προβλημάτων.

Τώρα ας δούμε γενικές μεθόδους για την επίλυση αυτών των προβλημάτων.

Οι απλούστερες αριθμητικές πράξεις με μιγαδικούς αριθμούς εκτελούνται σύμφωνα με τους κανόνες που περιγράφονται στην πρώτη ενότητα, αλλά εάν οι μιγαδικοί αριθμοί παρουσιάζονται σε τριγωνομετρικές ή εκθετικές μορφές, τότε σε αυτήν την περίπτωση μπορείτε να τους μετατρέψετε σε αλγεβρική μορφή και να εκτελέσετε πράξεις σύμφωνα με γνωστούς κανόνες.

Η εύρεση των ριζών των πολυωνύμων συνήθως καταλήγει στην εύρεση των ριζών μιας τετραγωνικής εξίσωσης. Ας υποθέσουμε ότι έχουμε μια τετραγωνική εξίσωση, αν η διάκρισή της είναι μη αρνητική, τότε οι ρίζες της θα είναι πραγματικές και μπορούν να βρεθούν σύμφωνα με έναν γνωστό τύπο. Εάν η διάκριση είναι αρνητική, δηλαδή, D = -1∙a 2, Οπου έναείναι ένας ορισμένος αριθμός, τότε το διακριτικό μπορεί να αναπαρασταθεί ως D = (ia) 2, ως εκ τούτου √D = i|a|, και στη συνέχεια μπορείτε να χρησιμοποιήσετε τον ήδη γνωστό τύπο για τις ρίζες μιας τετραγωνικής εξίσωσης.

Παράδειγμα. Ας επιστρέψουμε στην τετραγωνική εξίσωση που αναφέρθηκε παραπάνω x 2 + x + 1 = 0.
Διακριτικός - D = 1 - 4 ∙ 1 = -3 = -1(√3) 2 = (i√3) 2.
Τώρα μπορούμε εύκολα να βρούμε τις ρίζες:

Η αύξηση των μιγαδικών αριθμών σε δυνάμεις μπορεί να γίνει με διάφορους τρόπους. Εάν πρέπει να αυξήσετε έναν μιγαδικό αριθμό σε αλγεβρική μορφή σε μια μικρή δύναμη (2 ή 3), τότε μπορείτε να το κάνετε με άμεσο πολλαπλασιασμό, αλλά εάν η ισχύς είναι μεγαλύτερη (στα προβλήματα είναι συχνά πολύ μεγαλύτερη), τότε πρέπει να γράψτε αυτόν τον αριθμό σε τριγωνομετρικές ή εκθετικές μορφές και χρησιμοποιήστε ήδη γνωστές μεθόδους.

Παράδειγμα. Θεωρήστε z = 1 + i και ανεβάστε το στη δέκατη δύναμη.
Ας γράψουμε το z σε εκθετική μορφή: z = √2 e iπ/4.
Επειτα z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4.
Ας επιστρέψουμε στην αλγεβρική μορφή: z 10 = -32i.

Η εξαγωγή ριζών από μιγαδικούς αριθμούς είναι η αντίστροφη πράξη της εκθέσεως και επομένως εκτελείται με παρόμοιο τρόπο. Για την εξαγωγή ριζών, χρησιμοποιείται συχνά η εκθετική μορφή γραφής ενός αριθμού.

Παράδειγμα. Ας βρούμε όλες τις ρίζες του βαθμού 3 της ενότητας. Για να γίνει αυτό, θα βρούμε όλες τις ρίζες της εξίσωσης z 3 = 1, θα αναζητήσουμε τις ρίζες σε εκθετική μορφή.
Ας αντικαταστήσουμε στην εξίσωση: r 3 e 3iφ = 1 ή r 3 e 3iφ = e 0 .
Επομένως: r = 1, 3φ = 0 + 2πk, επομένως φ = 2πk/3.
Διαφορετικές ρίζες λαμβάνονται σε φ = 0, 2π/3, 4π/3.
Επομένως 1, e i2π/3, e i4π/3 είναι ρίζες.
Ή σε αλγεβρική μορφή:

Ο τελευταίος τύπος προβλημάτων περιλαμβάνει μια τεράστια ποικιλία προβλημάτων και δεν υπάρχουν γενικές μέθοδοι επίλυσής τους. Ας δώσουμε ένα απλό παράδειγμα μιας τέτοιας εργασίας:

Βρείτε το ποσό sin(x) + sin(2x) + sin(2x) + … + sin(nx).

Αν και η διατύπωση αυτού του προβλήματος δεν περιλαμβάνει μιγαδικούς αριθμούς, μπορεί εύκολα να λυθεί με τη βοήθειά τους. Για την επίλυσή του χρησιμοποιούνται οι ακόλουθες παραστάσεις:


Εάν τώρα αντικαταστήσουμε αυτήν την αναπαράσταση με το άθροισμα, τότε το πρόβλημα περιορίζεται στο άθροισμα της συνήθους γεωμετρικής προόδου.

συμπέρασμα

Οι μιγαδικοί αριθμοί χρησιμοποιούνται ευρέως στα μαθηματικά χρησιμοποιήστε εξειδικευμένη βιβλιογραφία.

Βιβλιογραφία

§ 1. Μιγαδικοί αριθμοί: ορισμοί, γεωμετρική ερμηνεία, ενέργειες σε αλγεβρικές, τριγωνομετρικές και εκθετικές μορφές

Ορισμός μιγαδικού αριθμού

Σύνθετες ισότητες

Γεωμετρική αναπαράσταση μιγαδικών αριθμών

Συντελεστής και όρισμα μιγαδικού αριθμού

Αλγεβρικές και τριγωνομετρικές μορφές μιγαδικού αριθμού

Εκθετική μορφή μιγαδικού αριθμού

Οι τύποι του Euler

§ 2. Ολόκληρες συναρτήσεις (πολυώνυμα) και οι βασικές τους ιδιότητες. Επίλυση αλγεβρικών εξισώσεων στο σύνολο των μιγαδικών αριθμών

Ορισμός αλγεβρικής εξίσωσης ου βαθμού

Βασικές ιδιότητες πολυωνύμων

Παραδείγματα επίλυσης αλγεβρικών εξισώσεων στο σύνολο των μιγαδικών αριθμών

Ερωτήσεις αυτοδιαγνωστικού ελέγχου

Γλωσσάριο

§ 1. Μιγαδικοί αριθμοί: ορισμοί, γεωμετρική ερμηνεία, ενέργειες σε αλγεβρικές, τριγωνομετρικές και εκθετικές μορφές

Ορισμός μιγαδικού αριθμού ( Να αναφέρετε τον ορισμό ενός μιγαδικού αριθμού)

Ένας μιγαδικός αριθμός z είναι μια έκφραση της ακόλουθης μορφής:

Μιγαδικός αριθμός σε αλγεβρική μορφή,(1)

Όπου x, y Î;

- σύνθετος συζευγμένος αριθμός αριθμός z ;

- αντίθετος αριθμός αριθμός z ;

- μιγαδικό μηδέν ;

– έτσι συμβολίζεται το σύνολο των μιγαδικών αριθμών.

1)z = 1 + ΕγώÞ Re z= 1, Im z = 1, = 1 – Εγώ, = –1 – Εγώ ;

2)z = –1 + ΕγώÞ Re z= –1, Im z = , = –1 – Εγώ, = –1 –Εγώ ;

3)z = 5 + 0Εγώ= 5 Þ Re z= 5, Im z = 0, = 5 – 0Εγώ = 5, = –5 – 0Εγώ = –5

Þ αν Im z= 0, λοιπόν z = Χ- πραγματικός αριθμός;

4)z = 0 + 3Εγώ = 3ΕγώÞ Re z= 0, Im z = 3, = 0 – 3Εγώ = –3Εγώ , = –0 – 3Εγώ = – 3Εγώ

Þ εάν Re z= 0, λοιπόν z = iy - καθαρά φανταστικός αριθμός.

Σύνθετες ισότητες (Διατυπώστε την έννοια της σύνθετης ισότητας)

1) ;

2) .

Μία σύνθετη ισότητα ισοδυναμεί με ένα σύστημα δύο πραγματικών ισοτήτων. Αυτές οι πραγματικές ισότητες λαμβάνονται από τη σύνθετη ισότητα διαχωρίζοντας το πραγματικό και το φανταστικό μέρος.

1) ;

2) .

Γεωμετρική αναπαράσταση μιγαδικών αριθμών ( Ποια είναι η γεωμετρική αναπαράσταση των μιγαδικών αριθμών;)

Μιγαδικός αριθμός zαντιπροσωπεύεται από μια τελεία ( Χ , y) στο μιγαδικό επίπεδο ή στο διάνυσμα ακτίνας αυτού του σημείου.

Σημάδι zστο δεύτερο τρίμηνο σημαίνει ότι το καρτεσιανό σύστημα συντεταγμένων θα χρησιμοποιηθεί ως σύνθετο επίπεδο.

Μέτρο και όρισμα μιγαδικού αριθμού ( Ποιο είναι το μέτρο και το όρισμα ενός μιγαδικού αριθμού;)

Το μέτρο ενός μιγαδικού αριθμού είναι ένας μη αρνητικός πραγματικός αριθμός

.(2)

Γεωμετρικά, το μέτρο συντελεστή ενός μιγαδικού αριθμού είναι το μήκος του διανύσματος που αντιπροσωπεύει τον αριθμό z, ή πολική ακτίνα ενός σημείου ( Χ , y).

Σχεδιάστε τους παρακάτω αριθμούς στο μιγαδικό επίπεδο και γράψτε τους σε τριγωνομετρική μορφή.

1)z = 1 + Εγώ Þ

,

Þ

Þ ;

,

Þ

Þ ;

,

5),

δηλαδή για z = 0 θα είναι

, ιαπροσδιόριστο.

Αριθμητικές πράξεις σε μιγαδικούς αριθμούς (Δώστε ορισμούς και απαριθμήστε τις κύριες ιδιότητες των αριθμητικών πράξεων σε μιγαδικούς αριθμούς.)

Πρόσθεση (αφαίρεση) μιγαδικών αριθμών

z 1 ± z 2 = (Χ 1 + iy 1) ± ( Χ 2 + iy 2) = (Χ 1 ± Χ 2) + Εγώ (y 1 ± y 2),(5)

δηλαδή κατά την πρόσθεση (αφαίρεση) μιγαδικών αριθμών προστίθενται (αφαιρούνται) τα πραγματικά και τα φανταστικά μέρη τους.

1)(1 + Εγώ) + (2 – 3Εγώ) = 1 + Εγώ + 2 –3Εγώ = 3 – 2Εγώ ;

2)(1 + 2Εγώ) – (2 – 5Εγώ) = 1 + 2Εγώ – 2 + 5Εγώ = –1 + 7Εγώ .

Βασικές ιδιότητες της προσθήκης

1)z 1 + z 2 = z 2 + z 1;

2)z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3);

3)z 1 – z 2 = z 1 + (– z 2);

4)z + (–z) = 0;

Πολλαπλασιασμός μιγαδικών αριθμών σε αλγεβρική μορφή

z 1∙z 2 = (Χ 1 + iy 1)∙(Χ 2 + iy 2) = Χ 1Χ 2 + Χ 1iy 2 + iy 1Χ 2 + Εγώ 2y 1y 2 = (6)

= (Χ 1Χ 2 – y 1y 2) + Εγώ (Χ 1y 2 + y 1Χ 2),

Δηλαδή, ο πολλαπλασιασμός μιγαδικών αριθμών σε αλγεβρική μορφή πραγματοποιείται σύμφωνα με τον κανόνα του αλγεβρικού πολλαπλασιασμού ενός διωνύμου με ένα διώνυμο, ακολουθούμενο από αντικατάσταση και αναγωγή παρόμοιων σε πραγματικούς και φανταστικούς όρους.

1)(1 + Εγώ)∙(2 – 3Εγώ) = 2 – 3Εγώ + 2Εγώ – 3Εγώ 2 = 2 – 3Εγώ + 2Εγώ + 3 = 5 – Εγώ ;

2)(1 + 4Εγώ)∙(1 – 4Εγώ) = 1 – 42 Εγώ 2 = 1 + 16 = 17;

3)(2 + Εγώ)2 = 22 + 4Εγώ + Εγώ 2 = 3 + 4Εγώ .

Πολλαπλασιασμός μιγαδικών αριθμών σε τριγωνομετρική μορφή

z 1∙z 2 = r 1 (συν ι 1 + Εγώαμαρτία ι 1)× r 2 (συν ι 2 + Εγώαμαρτία ι 2) =

= r 1r 2 (συν ι 1cos ι 2 + Εγώ cos ι 1 αμαρτία ι 2 + Εγώαμαρτία ι 1cos ι 2 + Εγώ 2 αμαρτία ι 1 αμαρτία ι 2) =

= r 1r 2 ((συν ι 1cos ι 2 – αμαρτία ι 1 αμαρτία ι 2) + Εγώ(συν ι 1 αμαρτία ι 2 + αμαρτία ι 1cos ι 2))

Το γινόμενο μιγαδικών αριθμών σε τριγωνομετρική μορφή, δηλαδή κατά τον πολλαπλασιασμό των μιγαδικών αριθμών σε τριγωνομετρική μορφή, οι ενότητες τους πολλαπλασιάζονται και προστίθενται τα ορίσματά τους.

Βασικές ιδιότητες του πολλαπλασιασμού

1)z 1× z 2 = z 2× z 1 - ανταλλαγή.

2)z 1× z 2× z 3 = (z 1× z 2)× z 3 = z 1×( z 2× z 3) - συνειρμικότητα.

3)z 1×( z 2 + z 3) = z 1× z 2 + z 1× z 3 - Κατανομή σε σχέση με την προσθήκη.

4)z×0 = 0; z×1 = z ;

Διαίρεση μιγαδικών αριθμών

Η διαίρεση είναι η αντίστροφη πράξη του πολλαπλασιασμού, άρα

Αν z × z 2 = z 1 και z 2 ¹ 0, τότε .

Όταν εκτελείτε διαίρεση σε αλγεβρική μορφή, ο αριθμητής και ο παρονομαστής του κλάσματος πολλαπλασιάζονται με το μιγαδικό συζυγές του παρονομαστή:

Διαίρεση μιγαδικών αριθμών σε αλγεβρική μορφή.(7)

Όταν εκτελείτε διαίρεση σε τριγωνομετρική μορφή, οι μονάδες διαιρούνται και αφαιρούνται τα ορίσματα:

Διαίρεση μιγαδικών αριθμών σε τριγωνομετρική μορφή.(8)

2)
.

Αύξηση μιγαδικού αριθμού σε φυσική δύναμη

Είναι πιο βολικό να εκτελείτε την εκθέτηση σε τριγωνομετρική μορφή:

Ο τύπος του Moivre, (9)

Δηλαδή, όταν ένας μιγαδικός αριθμός αυξάνεται σε μια φυσική ισχύ, το μέτρο του αυξάνεται σε αυτή τη δύναμη και το όρισμα πολλαπλασιάζεται με τον εκθέτη.

Υπολογίστε (1 + Εγώ)10.

Σημειώσεις

1. Κατά την εκτέλεση των πράξεων πολλαπλασιασμού και αύξησης σε φυσική ισχύ σε τριγωνομετρική μορφή, μπορούν να ληφθούν τιμές γωνίας πέρα ​​από μία πλήρη περιστροφή. Αλλά μπορούν πάντα να μειωθούν σε γωνίες ή ρίχνοντας έναν ακέραιο αριθμό πλήρους περιστροφών χρησιμοποιώντας τις ιδιότητες περιοδικότητας των συναρτήσεων και .

2. Έννοια ονομάζεται η κύρια τιμή του ορίσματος ενός μιγαδικού αριθμού.

Στην περίπτωση αυτή, οι τιμές όλων των πιθανών γωνιών συμβολίζονται με ;

είναι προφανές ότι, .

Εξαγωγή της ρίζας ενός φυσικού βαθμού από έναν μιγαδικό αριθμό

Οι τύποι του Euler (16)

για τις οποίες οι τριγωνομετρικές συναρτήσεις και μια πραγματική μεταβλητή εκφράζονται μέσω μιας εκθετικής συνάρτησης (εκθέτης) με έναν καθαρά φανταστικό εκθέτη.

§ 2. Ολόκληρες συναρτήσεις (πολυώνυμα) και οι βασικές τους ιδιότητες. Επίλυση αλγεβρικών εξισώσεων στο σύνολο των μιγαδικών αριθμών

Δύο πολυώνυμα του ίδιου βαθμού nείναι πανομοιότυπα ίσα μεταξύ τους αν και μόνο αν οι συντελεστές τους συμπίπτουν για τις ίδιες δυνάμεις της μεταβλητής Χ, αυτό είναι

Απόδειξη

w Η ταυτότητα (3) ισχύει για "xО (ή "xО)

Þ ισχύει για ; αντικαθιστώντας , παίρνουμε ένα = bn .

Ας ακυρώσουμε αμοιβαία τους όρους στο (3) έναΚαι bnκαι διαιρέστε και τα δύο μέρη με Χ :

Αυτή η ταυτότητα ισχύει επίσης για " Χ, συμπεριλαμβανομένου του πότε Χ = 0

Þ υποθέτοντας Χ= 0, παίρνουμε ένα – 1 = bn – 1.

Ας ακυρώσουμε αμοιβαία τους όρους στο (3") ένα– 1 και ένα n– 1 και χωρίζουμε και τις δύο πλευρές κατά Χ, ως αποτέλεσμα παίρνουμε

Συνεχίζοντας το επιχείρημα παρομοίως, λαμβάνουμε ότι ένα – 2 = bn –2, …, ΕΝΑ 0 = σι 0.

Έτσι, έχει αποδειχθεί ότι η πανομοιότυπη ισότητα των 2-x πολυωνύμων συνεπάγεται τη σύμπτωση των συντελεστών τους στις ίδιες μοίρες Χ .

Η αντίστροφη δήλωση είναι δικαίως προφανής, δηλ. εάν δύο πολυώνυμα έχουν τους ίδιους συντελεστές, τότε είναι πανομοιότυπες συναρτήσεις, επομένως, οι τιμές τους συμπίπτουν για όλες τις τιμές του ορίσματος, πράγμα που σημαίνει ότι είναι πανομοιότυπα ίσες. Η ιδιότητα 1 έχει αποδειχθεί πλήρως. v

Κατά τη διαίρεση ενός πολυωνύμου Πν (Χ) με τη διαφορά ( Χ – Χ 0) το υπόλοιπο είναι ίσο με Πν (Χ 0), δηλαδή

Θεώρημα Bezout, (4)

Οπου Qn – 1(Χ) - το ακέραιο μέρος της διαίρεσης, είναι ένα πολυώνυμο βαθμού ( n – 1).

Απόδειξη

w Ας γράψουμε τον τύπο διαίρεσης με υπόλοιπο:

Πν (Χ) = (Χ – Χ 0)∙Qn – 1(Χ) + ΕΝΑ ,

Οπου Qn – 1(Χ) - πολυώνυμο βαθμού ( n – 1),

ΕΝΑ- το υπόλοιπο, που είναι ένας αριθμός που οφείλεται στον γνωστό αλγόριθμο για τη διαίρεση ενός πολυωνύμου με ένα διώνυμο «σε στήλη».

Αυτή η ισότητα ισχύει για " Χ, συμπεριλαμβανομένου του πότε Χ = Χ 0 Þ

Πν (Χ 0) = (Χ 0 – Χ 0)× Qn – 1(Χ 0) + ΕΝΑ Þ

ΕΝΑ = Πν (Χ 0), κ.λπ. v

Συμπέρασμα του θεωρήματος του Bezout. Σχετικά με τη διαίρεση ενός πολυωνύμου με ένα διώνυμο χωρίς υπόλοιπο

Εάν ο αριθμός Χ 0 είναι το μηδέν ενός πολυωνύμου, τότε αυτό το πολυώνυμο διαιρείται με τη διαφορά ( Χ – Χ 0) χωρίς υπόλοιπο, δηλαδή

Þ .(5)

1), αφού Π 3(1) º 0

2) επειδή Π 4(–2) º 0

3) επειδή Π 2(–1/2) º 0

Διαίρεση πολυωνύμων σε διώνυμα "σε στήλη":

_

_

_

_

_

Κάθε πολυώνυμο βαθμού n ³ 1 έχει τουλάχιστον ένα μηδέν, πραγματικό ή μιγαδικό

Η απόδειξη αυτού του θεωρήματος ξεφεύγει από το εύρος της πορείας μας. Επομένως, δεχόμαστε το θεώρημα χωρίς απόδειξη.

Ας δουλέψουμε αυτό το θεώρημα και το θεώρημα του Bezout με το πολυώνυμο Πν (Χ).

Μετά n-πολλαπλή εφαρμογή αυτών των θεωρημάτων προκύπτει ότι

Οπου ένα 0 είναι ο συντελεστής στο Χ n V Πν (Χ).

Συμπέρασμα στο θεμελιώδες θεώρημα της άλγεβρας. Σχετικά με την αποσύνθεση ενός πολυωνύμου σε γραμμικούς παράγοντες

Οποιοδήποτε πολυώνυμο βαθμού στο σύνολο των μιγαδικών αριθμών μπορεί να αποσυντεθεί σε nγραμμικούς παράγοντες, δηλαδή

Επέκταση ενός πολυωνύμου σε γραμμικούς παράγοντες, (6)

όπου x1, x2, ... xn είναι τα μηδενικά του πολυωνύμου.

Επιπλέον, εάν καριθμοί από το σετ Χ 1, Χ 2, … xnσυμπίπτουν μεταξύ τους και με τον αριθμό α, μετά στο γινόμενο (6) ο πολλαπλασιαστής ( Χ- ένα) κ. Μετά ο αριθμός Χ= α λέγεται k-πλάση μηδέν του πολυωνύμου Πν ( Χ) . Αν κ= 1, τότε καλείται το μηδέν απλό μηδέν του πολυωνύμου Πν ( Χ) .

1)Π 4(Χ) = (Χ – 2)(Χ– 4)3 Þ Χ 1 = 2 - απλό μηδέν, Χ 2 = 4 - τριπλό μηδέν.

2)Π 4(Χ) = (Χ – Εγώ)4 Þ Χ = Εγώ- μηδενική πολλαπλότητα 4.

Ιδιότητα 4 (σχετικά με τον αριθμό των ριζών μιας αλγεβρικής εξίσωσης)

Οποιαδήποτε αλγεβρική εξίσωση Pn(x) = 0 του βαθμού n έχει ακριβώς n ρίζες στο σύνολο των μιγαδικών αριθμών, αν μετρήσουμε κάθε ρίζα τόσες φορές όση η πολλαπλότητα της.

1)Χ 2 – 4Χ+ 5 = 0 - αλγεβρική εξίσωση δεύτερου βαθμού

Þ Χ 1,2 = 2 ± = 2 ± Εγώ- δύο ρίζες.

2)Χ 3 + 1 = 0 - αλγεβρική εξίσωση τρίτου βαθμού

Þ Χ 1,2,3 = - τρεις ρίζες.

3)Π 3(Χ) = Χ 3 + Χ 2 – Χ– 1 = 0 Þ Χ 1 = 1, γιατί Π 3(1) = 0.

Διαιρέστε το πολυώνυμο Π 3(Χ) επί ( Χ – 1):

Χ 3	+	Χ 2	–	Χ	–	1	Χ – 1
Χ 3	–	Χ 2	Χ 2 + 2Χ +1
2Χ 2	–	Χ
2Χ 2	–	2Χ
Χ	–	1
Χ	–	1
0

Αρχική εξίσωση

Π 3(Χ) = Χ 3 + Χ 2 – Χ– 1 = 0 Û( Χ – 1)(Χ 2 + 2Χ+ 1) = 0 Û( Χ – 1)(Χ + 1)2 = 0

Þ Χ 1 = 1 - απλή ρίζα, Χ 2 = –1 - διπλή ρίζα.

1) – ζευγαρωμένες σύνθετες συζυγείς ρίζες.

Οποιοδήποτε πολυώνυμο με πραγματικούς συντελεστές διασπάται στο γινόμενο γραμμικών και τετραγωνικών συναρτήσεων με πραγματικούς συντελεστές.

Απόδειξη

w Αφήστε Χ 0 = ένα + δι- μηδέν πολυωνύμου Πν (Χ). Αν όλοι οι συντελεστές αυτού του πολυωνύμου είναι πραγματικοί αριθμοί, τότε είναι επίσης μηδέν (με την ιδιότητα 5).

Ας υπολογίσουμε το γινόμενο των διωνύμων :

πολυωνυμική εξίσωση μιγαδικών αριθμών

Πήρα ( Χ – ένα)2 + σι 2 - τετράγωνο τριώνυμο με πραγματικούς συντελεστές.

Έτσι, οποιοδήποτε ζεύγος διωνύμων με σύνθετες συζυγείς ρίζες στον τύπο (6) οδηγεί σε ένα τετραγωνικό τριώνυμο με πραγματικούς συντελεστές. v

1)Π 3(Χ) = Χ 3 + 1 = (Χ + 1)(Χ 2 – Χ + 1);

2)Π 4(Χ) = Χ 4 – Χ 3 + 4Χ 2 – 4Χ = Χ (Χ –1)(Χ 2 + 4).

Παραδείγματα επίλυσης αλγεβρικών εξισώσεων στο σύνολο μιγαδικών αριθμών ( Δώστε παραδείγματα επίλυσης αλγεβρικών εξισώσεων στο σύνολο των μιγαδικών αριθμών)

1. Αλγεβρικές εξισώσεις πρώτου βαθμού:

, είναι η μόνη απλή ρίζα.

2. Τετραγωνικές εξισώσεις:

, – έχει πάντα δύο ρίζες (διαφορετικές ή ίσες).

1) .

3. Διωνυμικές εξισώσεις βαθμού:

, – έχει πάντα διαφορετικές ρίζες.

,

Απάντηση:, .

4. Λύστε την κυβική εξίσωση.

Μια εξίσωση τρίτου βαθμού έχει τρεις ρίζες (πραγματικές ή μιγαδικές) και πρέπει να μετρήσετε κάθε ρίζα τόσες φορές όση η πολλαπλότητα της. Εφόσον όλοι οι συντελεστές αυτής της εξίσωσης είναι πραγματικοί αριθμοί, οι μιγαδικές ρίζες της εξίσωσης, εάν υπάρχουν, θα είναι μιγαδικές συζυγείς ζεύγους.

Με επιλογή βρίσκουμε την πρώτη ρίζα της εξίσωσης, αφού .

Συνεπεία του θεωρήματος του Bezout. Υπολογίζουμε αυτή τη διαίρεση "σε στήλη":

_
_
_

Τώρα αντιπροσωπεύοντας το πολυώνυμο ως γινόμενο ενός γραμμικού και ενός τετραγώνου παράγοντα, παίρνουμε:

.

Βρίσκουμε άλλες ρίζες ως ρίζες μιας τετραγωνικής εξίσωσης:

Απάντηση:, .

5. Κατασκευάστε αλγεβρική εξίσωση μικρότερου βαθμού με πραγματικούς συντελεστές, αν είναι γνωστό ότι οι αριθμοί Χ 1 = 3 και Χ 2 = 1 + Εγώείναι οι ρίζες του, και ΧΤο 1 είναι διπλή ρίζα και Χ 2 - απλό.

Ο αριθμός είναι και η ρίζα της εξίσωσης, γιατί οι συντελεστές της εξίσωσης πρέπει να είναι πραγματικοί.

Συνολικά, η απαιτούμενη εξίσωση έχει 4 ρίζες: Χ 1, Χ 1,Χ 2, . Άρα ο βαθμός του είναι 4. Συνθέτουμε πολυώνυμο 4ου βαθμού με μηδενικά Χ

11. Τι είναι το μιγαδικό μηδέν;

13. Να διατυπώσετε την έννοια της σύνθετης ισότητας.

15. Ποιο είναι το μέτρο και το όρισμα ενός μιγαδικού αριθμού;

17. Ποιο είναι το όρισμα ενός μιγαδικού αριθμού;

18. Ποιο είναι το όνομα ή η έννοια του τύπου;

19. Εξηγήστε την έννοια του συμβολισμού σε αυτόν τον τύπο:

27. Δώστε ορισμούς και απαριθμήστε τις κύριες ιδιότητες των αριθμητικών πράξεων σε μιγαδικούς αριθμούς.

28. Ποιο είναι το όνομα ή η έννοια του τύπου;

29. Εξηγήστε την έννοια του συμβολισμού σε αυτόν τον τύπο:

31. Ποιο είναι το όνομα ή η έννοια του τύπου;

32. Εξηγήστε την έννοια του συμβολισμού σε αυτόν τον τύπο:

34. Ποιο είναι το όνομα ή η έννοια του τύπου;

35. Εξηγήστε την έννοια του συμβολισμού σε αυτόν τον τύπο:

61. Να αναφέρετε τις κύριες ιδιότητες των πολυωνύμων.

63. Να αναφέρετε την ιδιότητα για τη διαίρεση ενός πολυωνύμου με τη διαφορά (x – x0).

65. Ποιο είναι το όνομα ή η σημασία του τύπου;

66. Εξηγήστε την έννοια του συμβολισμού σε αυτόν τον τύπο:

67. ⌂ .

69. Να αναφέρετε το θεώρημα: το βασικό θεώρημα της άλγεβρας.

70. Ποιο είναι το όνομα ή η έννοια του τύπου;

71. Εξηγήστε την έννοια του συμβολισμού σε αυτόν τον τύπο:

75. Να δηλώσετε την ιδιότητα για τον αριθμό των ριζών μιας αλγεβρικής εξίσωσης.

78. Να αναφέρετε την ιδιότητα για την αποσύνθεση πολυωνύμου με πραγματικούς συντελεστές σε γραμμικούς και τετραγωνικούς συντελεστές.

Γλωσσάριο

Το k-πτυχίο μηδέν ενός πολυωνύμου είναι... (σελ. 18)

ένα αλγεβρικό πολυώνυμο λέγεται... (σελ. 14)

μια αλγεβρική εξίσωση n ου βαθμού λέγεται... (σελ. 14)

η αλγεβρική μορφή ενός μιγαδικού αριθμού ονομάζεται... (σελ. 5)

το όρισμα ενός μιγαδικού αριθμού είναι... (σελίδα 4)

το πραγματικό μέρος ενός μιγαδικού αριθμού z είναι... (σελίδα 2)

ένας σύνθετος συζευγμένος αριθμός είναι... (σελίδα 2)

Το μιγαδικό μηδέν είναι... (σελίδα 2)

ένας μιγαδικός αριθμός ονομάζεται... (σελίδα 2)

μια ρίζα του βαθμού n ενός μιγαδικού αριθμού ονομάζεται... (σελ. 10)

η ρίζα της εξίσωσης είναι... (σελ. 14)

οι συντελεστές του πολυωνύμου είναι... (σελ. 14)

η φανταστική μονάδα είναι... (σελίδα 2)

το φανταστικό μέρος ενός μιγαδικού αριθμού z είναι... (σελίδα 2)

το μέτρο ενός μιγαδικού αριθμού ονομάζεται... (σελ. 4)

το μηδέν μιας συνάρτησης λέγεται... (σελ. 14)

η εκθετική μορφή ενός μιγαδικού αριθμού ονομάζεται... (σελ. 11)

ένα πολυώνυμο λέγεται... (σελ. 14)

ένα απλό μηδέν ενός πολυωνύμου λέγεται... (σελ. 18)

ο αντίθετος αριθμός είναι... (σελίδα 2)

ο βαθμός ενός πολυωνύμου είναι... (σελ. 14)

η τριγωνομετρική μορφή ενός μιγαδικού αριθμού ονομάζεται... (σελ. 5)

Ο τύπος του Moivre είναι... (σελ. 9)

Οι τύποι του Euler είναι... (σελίδα 13)

μια ολόκληρη συνάρτηση ονομάζεται... (σελ. 14)

ένας καθαρά φανταστικός αριθμός είναι... (σελ. 2)