Προσδιορισμός τομής ευθείας και επιπέδου. Επιστημονική ηλεκτρονική βιβλιοθήκη. Ειδικές περιπτώσεις αμοιβαίου παραλληλισμού και καθετότητας ευθείας και επιπέδου. ειδικές περιπτώσεις αμοιβαίας καθετότητας δύο επιπέδων

Η γραμμή τομής δύο επιπέδων είναι ευθεία. Ας εξετάσουμε πρώτα την ειδική περίπτωση (Εικ. 3.9), όταν ένα από τα τεμνόμενα επίπεδα είναι παράλληλο στο οριζόντιο επίπεδο των προεξοχών (α π 1, f 0 α X). Στην περίπτωση αυτή, η γραμμή τομής a, που ανήκει στο αεροπλάνοα, θα είναι επίσης παράλληλο στο επίπεδο π 1, (Εικ. 3.9. α), δηλαδή θα συμπίπτει με την οριζόντια των επιπέδων που τέμνονται (a ≡ h).

Εάν ένα από τα επίπεδα είναι παράλληλο στο μετωπικό επίπεδο των προεξοχών (Εικ. 3.9. β), τότε η γραμμή τομής a που ανήκει σε αυτό το επίπεδο θα είναι παράλληλη με το επίπεδο π 2 και θα συμπίπτει με το μετωπικό των τεμνόμενων επιπέδων (α ≡ στ).

.

.

Ρύζι. 3.9. Ειδική περίπτωσητομή του επιπέδου γενικής θέσης με τα επίπεδα: α - οριζόντιο επίπεδο. β - μετωπικό επίπεδο

Ένα παράδειγμα κατασκευής του σημείου τομής (K) της ευθείας γραμμής a (AB) με το επίπεδο α (DEF) φαίνεται στο Σχ. 3.10. Για να γίνει αυτό, η ευθεία α περικλείεται σε ένα αυθαίρετο επίπεδο β και προσδιορίζεται η γραμμή τομής των επιπέδων α και β.

Στο υπό εξέταση παράδειγμα, οι ευθείες γραμμές ΑΒ και ΜΝ ανήκουν στο ίδιο επίπεδο β και τέμνονται στο σημείο Κ, και εφόσον η ευθεία ΜΝ ανήκει σε ένα δεδομένο επίπεδο α (DEF), το σημείο Κ είναι επίσης το σημείο τομής της ευθείας α. (ΑΒ) με επίπεδο α. (Εικ. 3.11).

.

Ρύζι. 3.10. Κατασκευή του σημείου τομής μιας ευθείας και ενός επιπέδου

Για να λύσετε ένα τέτοιο πρόβλημα σε ένα σύνθετο σχέδιο, πρέπει να είστε σε θέση να βρείτε το σημείο τομής μιας ευθείας γραμμής σε γενική θέση με ένα επίπεδο σε γενική θέση.

Ας εξετάσουμε ένα παράδειγμα εύρεσης του σημείου τομής της ευθείας ΑΒ με το επίπεδο του τριγώνου DEF που φαίνεται στο Σχ. 3.11.

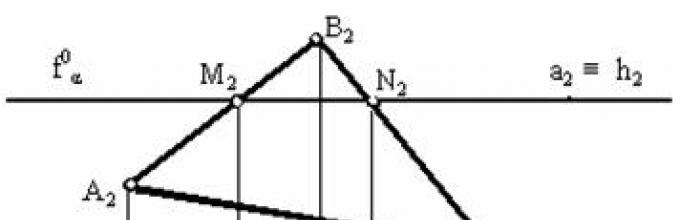
Για να βρεθεί το σημείο τομής μέσω της μετωπικής προβολής της ευθείας γραμμής A 2 B 2, σχεδιάστηκε ένα μετωπικά προεξέχον επίπεδο β το οποίο τέμνει το τρίγωνο στα σημεία M και N. Στο μετωπικό επίπεδο προβολής (π 2), αυτά τα σημεία αντιπροσωπεύονται από προεξοχές Μ 2, Ν 2. Από την συνθήκη να ανήκεις σε ευθύ επίπεδο στο οριζόντιο επίπεδο προεξοχών (π 1), βρίσκονται οριζόντιες προεξοχές των σημείων που προκύπτουν M 1 N 1. Στη διασταύρωση των οριζόντιων προεξοχών των ευθειών Α 1 Β 1 και Μ 1 Ν 1 σχηματίζεται οριζόντια προβολή του σημείου τομής τους (Κ 1). Σύμφωνα με τη γραμμή επικοινωνίας και τις συνθήκες ένταξης στο μετωπικό επίπεδο των προβολών, υπάρχει μετωπική προβολή του σημείου τομής (Κ 2).

.

Ρύζι. 3.11. Ένα παράδειγμα προσδιορισμού του σημείου τομής μιας ευθείας και ενός επιπέδου

Η ορατότητα του τμήματος ΑΒ σε σχέση με το τρίγωνο DEF προσδιορίζεται με τη μέθοδο του ανταγωνιστικού σημείου.

Στο επίπεδο π 2 θεωρούνται δύο σημεία NEF και 1AB. Από τις οριζόντιες προβολές αυτών των σημείων, μπορεί να διαπιστωθεί ότι το σημείο N βρίσκεται πιο κοντά στον παρατηρητή (Y N >Y 1) από το σημείο 1 (η κατεύθυνση της οπτικής γραμμής είναι παράλληλη προς το S). Κατά συνέπεια, η ευθεία ΑΒ, δηλαδή μέρος της ευθείας ΑΒ (Κ 1) καλύπτεται από το επίπεδο DEF στο επίπεδο π 2 (η προβολή της Κ 2 1 2 φαίνεται από τη διακεκομμένη γραμμή). Η ορατότητα στο επίπεδο π 1 καθορίζεται ομοίως.

Ερωτήσεις για αυτοέλεγχο

1) Ποια είναι η ουσία της μεθόδου ανταγωνιστικών σημείων;

2) Ποιες ιδιότητες μιας ευθείας γνωρίζετε;

3) Ποιος είναι ο αλγόριθμος για τον προσδιορισμό του σημείου τομής μιας ευθείας και ενός επιπέδου;

4) Ποιες εργασίες ονομάζονται θέσεις;

5) Διατυπώστε τις προϋποθέσεις για να ανήκεις σε ευθύ επίπεδο.

Φέρνουμε στην προσοχή σας περιοδικά που εκδίδονται από τον εκδοτικό οίκο "Ακαδημία Φυσικών Επιστημών"

Είναι γνωστό ότι μια ευθεία τέμνει ένα επίπεδο εάν δεν ανήκει σε αυτό το επίπεδο και δεν είναι παράλληλη με αυτό. Ακολουθώντας τον παρακάτω αλγόριθμο, βρίσκουμε το σημείο τομής της ευθείας έναμε ένα γενικό επίπεδο α που ορίζεται από τα ίχνη h 0α , f 0α .

Αλγόριθμος

1. Μέσω απευθείας ένασχεδιάζουμε ένα βοηθητικό μετωπικά προεξέχον επίπεδο γ. Το σχήμα δείχνει τα ίχνη του h 0γ, f 0γ.
2. Κατασκευάζουμε προβολές ευθείας ΑΒ κατά μήκος της οποίας τέμνονται τα επίπεδα α και γ. Σε αυτό το πρόβλημα, το σημείο B" = h 0α ∩ h 0γ, A"" = f 0α ∩ f 0γ. Τα σημεία A" και B"" βρίσκονται στον άξονα x, η θέση τους καθορίζεται από τις γραμμές επικοινωνίας.
3. Απευθείας ένακαι ΑΒ τέμνονται στο επιθυμητό σημείο Κ. Η οριζόντια προβολή του K" = a" ∩ A"B". Η μετωπική προβολή Κ"" βρίσκεται στην ευθεία α"".

Ο αλγόριθμος επίλυσης θα παραμείνει ίδιος εάν το pl. Το α θα δίνεται με παράλληλες, διασταυρούμενες γραμμές, ένα τμήμα ενός σχήματος ή άλλα πιθανά μέσα.

Ορατότητα ευθείας α σε σχέση με το επίπεδο α. Μέθοδος Ανταγωνιστικών Πόντων

1. Ας σημειώσουμε τα μετωπικά ανταγωνιστικά σημεία Α και Γ στο σχέδιο (Εικ. παρακάτω). Θα υποθέσουμε ότι το σημείο Α ανήκει στην περιοχή. Το α, και το C βρίσκεται στην ευθεία a. Οι μετωπικές προεξοχές Α"" και Γ"" συμπίπτουν, αλλά ταυτόχρονα τα σημεία Α και Γ απομακρύνονται από το επίπεδο των προβολών P 2 σε διαφορετικές αποστάσεις.
2. Ας βρούμε τις οριζόντιες προβολές Α" και Γ". Όπως φαίνεται στο σχήμα, το σημείο C" αφαιρείται από το επίπεδο P 2 σε μεγαλύτερη απόσταση από το σημείο Α", που ανήκει στο τετράγωνο. α. Κατά συνέπεια, θα είναι ορατό ένα τμήμα της ευθείας α"", που βρίσκεται στα αριστερά του σημείου Κ"". Το τμήμα α"" στα δεξιά του Κ"" είναι αόρατο. Το σημειώνουμε με διακεκομμένη γραμμή.
3. Ας σημειώσουμε οριζόντια ανταγωνιστικά σημεία Δ και Ε στο σχέδιο. Θα υποθέσουμε ότι το σημείο Δ ανήκει στο τετράγωνο. Το α, και το Ε βρίσκεται στη γραμμή α. Οι οριζόντιες προβολές D" και E" συμπίπτουν, αλλά ταυτόχρονα τα σημεία D και E αφαιρούνται από το επίπεδο P 1 σε διαφορετικές αποστάσεις.
4. Ας προσδιορίσουμε τη θέση των μετωπικών προεξοχών D"" και E"". Όπως φαίνεται στο σχήμα, το σημείο Δ"», που βρίσκεται στο τετράγωνο. α, αφαιρείται από το επίπεδο P 1 σε απόσταση μεγαλύτερη από το σημείο Ε "", που ανήκει στην ευθεία α. Κατά συνέπεια, το τμήμα α" που βρίσκεται στα δεξιά του σημείου Κ" θα είναι αόρατο. Το σημειώνουμε με διακεκομμένη γραμμή. Το τμήμα α" στα αριστερά του Κ" είναι ορατό.

Δίνεται ευθεία: (1) και επίπεδο: Ax + By + Cz + D = 0 (2).

Ας βρούμε τις συντεταγμένες του σημείου τομής της ευθείας και του επιπέδου. Εάν η ευθεία (1) και το επίπεδο (2) τέμνονται, τότε οι συντεταγμένες του σημείου τομής ικανοποιούν τις εξισώσεις (1) και (2):

, .

Αντικαθιστώντας την ευρεθείσα τιμή του t σε (1), λαμβάνουμε τις συντεταγμένες του σημείου τομής.

1) Αν Am + Bn + Cp = 0, και Ax 0 + By 0 + Cz 0 + D ≠ 0, τότε το t δεν υπάρχει, δηλ. μια ευθεία και ένα επίπεδο δεν έχουν ένα κοινό σημείο. Είναι παράλληλοι.

2) Am + Bn + Cp = 0 και Ax 0 + By 0 + Cz 0 + D = 0. Σε αυτήν την περίπτωση, το t μπορεί να πάρει οποιεσδήποτε τιμές και, δηλ. μια ευθεία είναι παράλληλη με το επίπεδο και έχει κοινό σημέιο, δηλ. βρίσκεται σε ένα αεροπλάνο.

Παράδειγμα 1. Βρείτε το σημείο τομής μιας ευθείας με επίπεδο 3x – 3y + 2z – 5 = 0.

3(2t – 1) – 3(4t + 3) + 2 3t – 5 = 0 => -17=0, που είναι αδύνατο για οποιοδήποτε t, δηλ. μια ευθεία και ένα επίπεδο δεν τέμνονται.

Παράδειγμα 2. Να βρείτε το σημείο τομής μιας ευθείας και επίπεδα: x + 2y – 4z + 1 = 0.

8t + 13 + 2(2t + 1) – 4(3t + 4) + 1 = 0, 0 + 0 = 0. Αυτό ισχύει για οποιαδήποτε τιμή του t, δηλ. η ευθεία βρίσκεται στο επίπεδο.

Παράδειγμα 3. Να βρείτε το σημείο τομής μιας ευθείας και επίπεδο 3x – y + 2z – 5 = 0.

3(5t + 7) – t – 4 + 2(4t + 5) – 5 = 0, 22t + 22 = 0, t = -1, x = 5(-1) + 7 = 2, y = -1 + 4 = 3, z = 4(-1) + 5 = 1, M(2, 3, 1) – το σημείο τομής της ευθείας και του επιπέδου.

Η γωνία μεταξύ ευθείας γραμμής και επιπέδου. Προϋποθέσεις παραλληλισμού και καθετότητας ευθείας και επιπέδου.

Η γωνία μεταξύ ευθείας γραμμής και επιπέδου ονομάζεται αιχμηρή γωνία q μεταξύ μιας ευθείας γραμμής και της προβολής της σε ένα επίπεδο.

Έστω μια ευθεία γραμμή και ένα επίπεδο:

Και .

Αφήστε την ευθεία να τέμνει το επίπεδο και να σχηματίσει μια γωνία μ () με αυτήν. Τότε b = 90 0 – q ή b = 90 0 + q είναι η γωνία μεταξύ του κανονικού διανύσματος του επιπέδου και του κατευθυντικού διανύσματος της ευθείας. Αλλά . Που σημαίνει

(3).

α) Αν L P, τότε - η συνθήκη της καθετότητας μιας ευθείας και ενός επιπέδου.

β) Αν L||P, τότε είναι η προϋπόθεση για τον παραλληλισμό της ευθείας και του επιπέδου.

γ) Αν η ευθεία είναι L||P και ταυτόχρονα το σημείο M0(x0, y0, z0) P, τότε η ευθεία βρίσκεται σε αυτό το επίπεδο. Αναλυτικά:

- προϋποθέσεις για να ανήκεις σε ευθεία γραμμή και επίπεδο.

Παράδειγμα. Δίνεται ευθεία γραμμή και σημείο M 0 (1, 0, –2). Μέσα από το σημείο M 0 σχεδιάστε ένα επίπεδο κάθετο σε αυτή την ευθεία. Αναζητούμε την εξίσωση του επιθυμητού επιπέδου με τη μορφή: A(x – 1) + B(y – 0) + C(z + 2) = 0. Στην περίπτωση αυτή , ,

5(x – 1) – 5y + 5(z + 2) = 0, - x – y + z + 3 = 0.

Ένα μάτσο αεροπλάνα.

Μια δέσμη επιπέδων είναι το σύνολο όλων των επιπέδων που διέρχονται από μια δεδομένη ευθεία - τον άξονα της δέσμης.

Για να ορίσετε μια δέσμη επιπέδων, αρκεί να καθορίσετε τον άξονά της. Έστω η εξίσωση αυτής της γραμμής σε γενική μορφή:

.

Για να συνθέσετε μια εξίσωση δέσμης σημαίνει να συνθέσετε μια εξίσωση από την οποία μπορεί κανείς να λάβει πρόσθετη προϋπόθεσηεξίσωση οποιουδήποτε επιπέδου της δοκού, εκτός από το β.μ. ένας. Ας πολλαπλασιάσουμε την εξίσωση II επί l και ας την προσθέσουμε στην εξίσωση I:

A 1 x + B 1 y + C 1 z + D 1 + l(A 2 x + B 2 y + C 2 z + D 2) = 0 (1) ή

(A 1 + lA 2)x + (B 1 + lB 2)y + (C 1 + lC 2)z + (D 1 + lD 2) = 0 (2).

l – παράμετρος – αριθμός που μπορεί να πάρει πραγματικές τιμές. Για οποιαδήποτε επιλεγμένη τιμή του l, οι εξισώσεις (1) και (2) είναι γραμμικές, δηλ. αυτές είναι οι εξισώσεις ενός συγκεκριμένου επιπέδου.

1. Ας δείξουμε ότι αυτό το επίπεδο διέρχεται από τον άξονα δέσμης L. Πάρτε ένα αυθαίρετο σημείο M 0 (x 0, y 0, z 0) L. Κατά συνέπεια, M 0 P 1 και M 0 P 2. Που σημαίνει:

3x – y + 2z + 9 + 17x + 17z – 51 = 0; 20x – y + 19z – 42 = 0.

Παράδειγμα 3 (Ε). Γράψτε μια εξίσωση για ένα επίπεδο που διέρχεται από μια ευθεία κάθετη στο επίπεδο x – 2y + z + 5 = 0. ; 3x – 2y + z – 3 + l(x – 2z) = 0; (3 + l)x – 2y + (1 – 2 l)z – 3 = 0; ; ; l = 8; 11x – 2y – 15z – 3 = 0.

77*. Βρείτε το σημείο τομής της ευθείας ΑΒ με το επίπεδο που ορίζεται από το τρίγωνο CDE (Εικ. 75, α).

Λύση. Όπως είναι γνωστό, για να βρεθεί το σημείο τομής μιας ευθείας με ένα γενικό επίπεδο, πρέπει να σχεδιάσουμε ένα βοηθητικό επίπεδο (R) μέσω της ευθείας γραμμής, να κατασκευάσουμε μια γραμμή τομής αυτού του επιπέδου με μια δεδομένη (1-2) και βρείτε

το σημείο τομής (Κ) των δεδομένων και κατασκευασμένων ευθειών. Το σημείο Κ είναι το επιθυμητό σημείο τομής της ευθείας με το επίπεδο (Εικ. 75, β). Ένα οριζόντιο ή μετωπικό επίπεδο προβολής χρησιμοποιείται συνήθως ως βοηθητικό επίπεδο.

Στο Σχ. 75, στο c, ένα μετωπικά προεξέχον επίπεδο R τραβιέται μέσω της ευθείας AB, το ίχνος του R ϑ συμπίπτει με ένα "c". ορίζοντας. Το ίχνος του αεροπλάνου δεν χρειάζεται σε αυτό το πρόβλημα και επομένως δεν φαίνεται.

Κατασκευάζουμε τη γραμμή τομής του επιπέδου R και του επιπέδου που ορίζεται από το τρίγωνο CDE (για παράδειγμα τέτοιας κατασκευής, βλ. Πρόβλημα 67). Έχοντας κατασκευάσει τη γραμμή 1-2 (Εικ. 75, γ), βρίσκουμε το σημείο τομής του με την ευθεία ΑΒ - σημείο Κ (k, k").

Για να προσδιορίσετε τα τμήματα της ευθείας ΑΒ που θα καλύπτονται από ένα τρίγωνο, θα πρέπει να χρησιμοποιήσετε μια ανάλυση της θέσης των σημείων στις τεμνόμενες ευθείες.

Για παράδειγμα, τα σημεία 1 και 3 βρίσκονται στις τεμνόμενες ευθείες (αντίστοιχα) ΕΔ και ΑΒ. Οι μετωπικές προβολές αυτών των σημείων συμπίπτουν, δηλαδή τα σημεία 1 και 3 απέχουν εξίσου από το τετράγωνο. Ν. Αλλά οι αποστάσεις τους από την πλατεία. V είναι διαφορετικά: το σημείο 3 είναι πιο μακριά από το τετράγωνο. V παρά σημείο 1. Επομένως, σε σχέση με την πλ. Το σημείο V 3 καλύπτει το σημείο 1 (η κατεύθυνση θέασης υποδεικνύεται με το βέλος S). Κατά συνέπεια, η ευθεία ΑΒ περνά μπροστά από το τρίγωνο CDE στο σημείο Κ. Ξεκινώντας από το σημείο Κ προς τα αριστερά, η ευθεία ΑΒ καλύπτεται από ένα τρίγωνο και επομένως αυτό το τμήμα της ευθείας εμφανίζεται με μια διακεκομμένη γραμμή.

Να προσδιορίσει μια αόρατη περιοχή στον ορίζοντα. προβολές της ευθείας ΑΒ, θεωρήστε τα σημεία 4 και 5, που βρίσκονται αντίστοιχα στις ευθείες ΑΒ και ΓΔ.

Αν κοιτάξουμε αυτά τα σημεία προς την κατεύθυνση s 1, βλέπουμε πρώτα το σημείο 5. Το σημείο 4 καλύπτεται από το σημείο 5. Συνεπώς, η ευθεία ΑΒ σε αυτό το σημείο καλύπτεται από το τρίγωνο CDE και το τμήμα της προβολής του από το σημείο k στο σημείο Το 4 πρέπει να εμφανίζεται με διακεκομμένη γραμμή. Σε αυτή την περίπτωση, το σημείο Κ ήταν μέσα στο περίγραμμα του τριγώνου CDE.

Εάν η σχετική θέση των τεμνόμενων στοιχείων είναι διαφορετική, είναι πιθανό το σημείο Κ να βρίσκεται εκτός του τριγώνου (Εικ. 75, δ). Αυτό σημαίνει ότι η ευθεία ΑΒ τέμνει το επίπεδο που ορίζεται από το τρίγωνο CDE έξω από το περίγραμμα αυτού του τριγώνου. Το ΑΒ γίνεται αόρατο πίσω από το σημείο Κ (στα αριστερά).

78. Να βρείτε τα σημεία τομής της ευθείας ΑΒ με τις όψεις της πυραμίδας (Εικ. 76). Οι όψεις της πυραμίδας πρέπει να θεωρούνται ως επίπεδα που ορίζονται από τρίγωνα.

79. Να βρείτε τα σημεία τομής της ευθείας ΑΒ με τις όψεις του πρίσματος (Εικ. 77). Οι όψεις του πρίσματος πρέπει να θεωρούνται ως επίπεδα που ορίζονται από παράλληλες ευθείες γραμμές.

80*. Βρείτε τα σημεία τομής της ευθείας ΑΒ με το επίπεδο Ρ (Εικ. 78, α).

Λύση. Σχεδιάζουμε το μετωπικά προεξέχον επίπεδο R μέσω της ευθείας γραμμής AB (Εικ. 78, β) (το ίχνος του R ϑ συμπίπτει με ένα "b") και κατασκευάζουμε την ευθεία MN της τομής και των δύο επιπέδων - δεδομένη και διαγραμμένη μέσω AB (το η κατασκευή είναι παρόμοια με αυτή που εκτελέστηκε στο πρόβλημα 70). Το απαιτούμενο σημείο Κ(κ, κ") τομής της ευθείας ΑΒ με το επίπεδο Ρ βρίσκεται στο σημείο τομής της ΜΝ με την ΑΒ.

Σε αυτό το πρόβλημα, η ορατότητα του ευθύγραμμου τμήματος από το σημείο Α έως το Κ είναι προφανής. ωστόσο, περισσότερο δύσκολες περιπτώσειςτο ορατό τμήμα της ευθείας πρέπει να προσδιορίζεται με βάση

ανάλυση της θέσης των σημείων. Για παράδειγμα, λαμβάνοντας το σημείο 1 (στη γραμμή AB) και το σημείο N (στο ίχνος P ϑ). βλέπουμε ότι το σημείο 1 βρίσκεται περισσότερο σε σχέση με το τετράγωνο. V από το σημείο N. Επομένως, η ευθεία ΑΒ στο σημείο Κ είναι ορατή. Πέρα από το σημείο Κ, η ευθεία εμφανίζεται ως διακεκομμένη γραμμή και είναι αόρατη. Η ορατότητα στον ορίζοντα προσδιορίζεται με παρόμοιο τρόπο. προβολές.

81. Να βρείτε το σημείο τομής της ευθείας ΑΒ με το επίπεδο Ρ (Εικ. 79).

82*. Βρείτε το σημείο τομής της ευθείας ΑΒ με το επίπεδο Ρ (Εικ. 80, α).

Λύση. Μέσω της ευθείας AB σχεδιάζουμε ένα οριζόντια προεξέχον επίπεδο R (το ίχνος του R h συμπίπτει με το ab) και κατασκευάζουμε τη γραμμή τομής των επιπέδων P και R,

χρησιμοποιώντας τα σημεία Μ και Ν της τομής των ομώνυμων τροχιών τους (Εικ. 80, β και γ). Το επιθυμητό σημείο (k", k) βρίσκεται στο σημείο τομής του MN με το AB. Στο Σχ. 80, d, το σημείο K κατασκευάζεται χρησιμοποιώντας το διάγραμμα W. Εφόσον το διάγραμμα P είναι προεξέχον προφίλ (Εικ. 80, b).

τότε η προβολή προφίλ k" βρίσκεται στο σημείο τομής του ίχνους P ω με το a"b". Γνωρίζοντας το k", κατασκευάζουμε το k" στο a"b" και το k στο ab. Τα ορατά τμήματα της ευθείας ΑΒ είναι προσδιορίζεται με τον ίδιο τρόπο όπως στα προβλήματα 77 και 80.

83. Να βρείτε το σημείο τομής της ευθείας ΑΒ με το επίπεδο Ρ (Εικ. 81).

84*. Βρείτε το σημείο τομής της ευθείας ΑΒ με το επίπεδο που ορίζεται από το τρίγωνο CDE (Εικ. 82, α).

Λύση. Μέσω της ευθείας ΑΒ σχεδιάζουμε (Εικ. 82, β και γ) τετράγωνο. R, παράλληλα με το τετράγωνο W. Διασχίζει δεδομένο αεροπλάνοκατά μήκος της ευθείας MN (σημεία m", n", m και n βρίσκονται στη τομή των ιχνών R ϑ και R h με τις ίδιες προεξοχές των αντίστοιχων πλευρών

τρίγωνο CDE). Εφόσον οι ευθείες ΑΒ και ΜΝ είναι προφίλ, τότε για να βρούμε το σημείο (Κ) της τομής τους κατασκευάζουμε προβολές προφίλ a"b" και m"n". Η προβολή k" βρίσκεται στη διασταύρωση των a"b" και m"m". Χρησιμοποιώντας k" κατασκευάζουμε το k" στο a"b" και το k στο ab.

85. Να βρείτε το σημείο τομής της ευθείας EF με το επίπεδο που ορίζεται από το τετράπλευρο ABCD (Εικ. 83).