When solving many mathematical problems , especially those that occur before grade 10, the order of actions performed that will lead to the goal is clearly defined. Such problems include, for example, linear and quadratic equations, linear and quadratic inequalities, fractional equations and equations that reduce to quadratic. The principle of successfully solving each of the mentioned problems is as follows: it is necessary to establish what type of problem is being solved, remember the necessary sequence of actions that will lead to the desired result, i.e. answer and follow these steps.
It is obvious that success or failure in solving a particular problem depends mainly on how correctly the type of equation being solved is determined, how correctly the sequence of all stages of its solution is reproduced. Of course, it is necessary to have the skills to perform identity transformations and computing.
The situation is different with trigonometric equations. It is not at all difficult to establish the fact that the equation is trigonometric. Difficulties arise when determining the sequence of actions that would lead to the correct answer.
By appearance equation, it is sometimes difficult to determine its type. And without knowing the type of equation, it is almost impossible to choose the right one from several dozen trigonometric formulas.
To solve a trigonometric equation, you need to try:
1. bring all functions included in the equation to “the same angles”;
2. bring the equation to “identical functions”;
3. factor the left side of the equation, etc.
Let's consider basic methods for solving trigonometric equations.
I. Reduction to the simplest trigonometric equations
Solution diagram
Step 1. Express a trigonometric function in terms of known components.
Step 2. Find the function argument using the formulas:
cos x = a; x = ±arccos a + 2πn, n ЄZ.
sin x = a; x = (-1) n arcsin a + πn, n Є Z.
tan x = a; x = arctan a + πn, n Є Z.
ctg x = a; x = arcctg a + πn, n Є Z.
Step 3. Find the unknown variable.
Example.
2 cos(3x – π/4) = -√2.
Solution.
1) cos(3x – π/4) = -√2/2.
2) 3x – π/4 = ±(π – π/4) + 2πn, n Є Z;
3x – π/4 = ±3π/4 + 2πn, n Є Z.
3) 3x = ±3π/4 + π/4 + 2πn, n Є Z;
x = ±3π/12 + π/12 + 2πn/3, n Є Z;
x = ±π/4 + π/12 + 2πn/3, n Є Z.
Answer: ±π/4 + π/12 + 2πn/3, n Є Z.
II. Variable replacement
Solution diagram
Step 1. Reduce the equation to algebraic form with respect to one of the trigonometric functions.
Step 2. Denote the resulting function by the variable t (if necessary, introduce restrictions on t).
Step 3. Write down and solve the result algebraic equation.
Step 4. Make a reverse replacement.
Step 5. Solve the simplest trigonometric equation.
Example.
2cos 2 (x/2) – 5sin (x/2) – 5 = 0.
Solution.
1) 2(1 – sin 2 (x/2)) – 5sin (x/2) – 5 = 0;
2sin 2 (x/2) + 5sin (x/2) + 3 = 0.
2) Let sin (x/2) = t, where |t| ≤ 1.
3) 2t 2 + 5t + 3 = 0;
t = 1 or e = -3/2, does not satisfy the condition |t| ≤ 1.
4) sin(x/2) = 1.
5) x/2 = π/2 + 2πn, n Є Z;
x = π + 4πn, n Є Z.
Answer: x = π + 4πn, n Є Z.
III. Equation order reduction method
Solution diagram
Step 1. Replace this equation with a linear one, using the formula for reducing the degree:
sin 2 x = 1/2 · (1 – cos 2x);
cos 2 x = 1/2 · (1 + cos 2x);
tg 2 x = (1 – cos 2x) / (1 + cos 2x).
Step 2. Solve the resulting equation using methods I and II.
Example.
cos 2x + cos 2 x = 5/4.
Solution.
1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.
2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;
3/2 cos 2x = 3/4;
2x = ±π/3 + 2πn, n Є Z;
x = ±π/6 + πn, n Є Z.
Answer: x = ±π/6 + πn, n Є Z.
IV. Homogeneous equations
Solution diagram
Step 1. Reduce this equation to the form
a) a sin x + b cos x = 0 ( homogeneous equation first degree)
or to the view
b) a sin 2 x + b sin x · cos x + c cos 2 x = 0 (homogeneous equation of the second degree).
Step 2. Divide both sides of the equation by
a) cos x ≠ 0;
b) cos 2 x ≠ 0;
and get the equation for tan x:
a) a tan x + b = 0;
b) a tan 2 x + b arctan x + c = 0.
Step 3. Solve the equation using known methods.
Example.
5sin 2 x + 3sin x cos x – 4 = 0.
Solution.
1) 5sin 2 x + 3sin x · cos x – 4(sin 2 x + cos 2 x) = 0;
5sin 2 x + 3sin x · cos x – 4sin² x – 4cos 2 x = 0;
sin 2 x + 3sin x · cos x – 4cos 2 x = 0/cos 2 x ≠ 0.
2) tg 2 x + 3tg x – 4 = 0.
3) Let tg x = t, then
t 2 + 3t – 4 = 0;
t = 1 or t = -4, which means
tg x = 1 or tg x = -4.
From the first equation x = π/4 + πn, n Є Z; from the second equation x = -arctg 4 + πk, k Є Z.
Answer: x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.
V. Method of transforming an equation using trigonometric formulas
Solution diagram
Step 1. Using all sorts of trigonometric formulas, reduce this equation to an equation solved by methods I, II, III, IV.
Step 2. Solve the resulting equation using known methods.
Example.
sin x + sin 2x + sin 3x = 0.
Solution.
1) (sin x + sin 3x) + sin 2x = 0;
2sin 2x cos x + sin 2x = 0.
2) sin 2x (2cos x + 1) = 0;
sin 2x = 0 or 2cos x + 1 = 0;
From the first equation 2x = π/2 + πn, n Є Z; from the second equation cos x = -1/2.
We have x = π/4 + πn/2, n Є Z; from the second equation x = ±(π – π/3) + 2πk, k Є Z.
As a result, x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Answer: x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Solving skills and abilities trigonometric equations are very  important, their development requires significant effort, both on the part of the student and on the part of the teacher.
important, their development requires significant effort, both on the part of the student and on the part of the teacher.
Many problems of stereometry, physics, etc. are associated with the solution of trigonometric equations. The process of solving such problems embodies many of the knowledge and skills that are acquired by studying the elements of trigonometry.
Trigonometric equations occupy an important place in the process of learning mathematics and personal development in general.
Still have questions? Don't know how to solve trigonometric equations?
To get help from a tutor, register.
The first lesson is free!
website, when copying material in full or in part, a link to the source is required.
The main methods for solving trigonometric equations are: reducing the equations to the simplest (using trigonometric formulas), introducing new variables, and factoring. Let's look at their use with examples. Pay attention to the format of writing solutions to trigonometric equations.
A necessary condition for successfully solving trigonometric equations is knowledge of trigonometric formulas (topic 13 of work 6).
Examples.
1. Equations reduced to the simplest.
1) Solve the equation
Solution:
Answer:
2) Find the roots of the equation
(sinx + cosx) 2 = 1 – sinxcosx, belonging to the segment.
Solution:
Answer:
2. Equations that reduce to quadratic.
1) Solve the equation 2 sin 2 x – cosx –1 = 0.
Solution: Using the formula sin 2 x = 1 – cos 2 x, we get
Answer:
2) Solve the equation cos 2x = 1 + 4 cosx.
Solution: Using the formula cos 2x = 2 cos 2 x – 1, we get
Answer:
3) Solve the equation tgx – 2ctgx + 1 = 0
Solution:
Answer:
3. Homogeneous equations
1) Solve the equation 2sinx – 3cosx = 0
Solution: Let cosx = 0, then 2sinx = 0 and sinx = 0 – a contradiction with the fact that sin 2 x + cos 2 x = 1. This means cosx ≠ 0 and we can divide the equation by cosx. We get
Answer:
2) Solve the equation 1 + 7 cos 2 x = 3 sin 2x
Solution:
We use the formulas 1 = sin 2 x + cos 2 x and sin 2x = 2 sinxcosx, we get
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Let cosx = 0, then sin 2 x = 0 and sinx = 0 – a contradiction with the fact that sin 2 x + cos 2 x = 1.
This means cosx ≠ 0 and we can divide the equation by cos 2 x .
We get
tg 2 x – 6 tgx + 8 = 0
Let us denote tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2 = 2
a) tgx = 4, x= arctan4 + 2 k, k
b) tgx = 2, x= arctan2 + 2 k, k .
Answer: arctg4 + 2 k, arctan2 + 2 k, k
4. Equations of the form a sinx + b cosx = s, s≠ 0.
1) Solve the equation.
Solution:
Answer:
5. Equations solved by factorization.
1) Solve sin equation 2x – sinx = 0.
Root of the equation f (X) = φ ( X) can only serve as the number 0. Let's check this:
cos 0 = 0 + 1 – the equality is true.
The number 0 is the only root of this equation.
Answer: 0.
Concept of solving trigonometric equations.
- To solve a trigonometric equation, convert it into one or more basic trigonometric equations. Solving a trigonometric equation ultimately comes down to solving the four basic trigonometric equations.
Solving basic trigonometric equations.
- There are 4 types of basic trigonometric equations:
- sin x = a; cos x = a
- tan x = a; ctg x = a
- Solving basic trigonometric equations involves considering the different "x" positions on unit circle, and using a conversion table (or calculator).
- Example 1. sin x = 0.866. Using a conversion table (or calculator) you will get the answer: x = π/3. The unit circle gives another answer: 2π/3. Remember: everything trigonometric functions are periodic, that is, their values repeat. For example, the periodicity of sin x and cos x is 2πn, and the periodicity of tg x and ctg x is πn. Therefore the answer is written as follows:
- x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
- Example 2. cos x = -1/2. Using a conversion table (or calculator) you will get the answer: x = 2π/3. The unit circle gives another answer: -2π/3.
- x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
- Example 3. tg (x - π/4) = 0.
- Answer: x = π/4 + πn.
- Example 4. ctg 2x = 1.732.
- Answer: x = π/12 + πn.
Transformations used in solving trigonometric equations.
- To transform trigonometric equations, algebraic transformations are used (factorization, reduction homogeneous members etc.) and trigonometric identities.
- Example 5: Using trigonometric identities, the equation sin x + sin 2x + sin 3x = 0 is converted to the equation 4cos x*sin (3x/2)*cos (x/2) = 0. Thus, the following basic trigonometric equations need to be solved: cos x = 0; sin(3x/2) = 0; cos(x/2) = 0.
-
Finding angles using known function values.
- Before learning how to solve trigonometric equations, you need to learn how to find angles using known function values. This can be done using a conversion table or calculator.
- Example: cos x = 0.732. The calculator will give the answer x = 42.95 degrees. The unit circle will give additional angles, the cosine of which is also 0.732.
-
Set aside the solution on the unit circle.
- You can plot solutions to a trigonometric equation on the unit circle. Solutions to a trigonometric equation on the unit circle are the vertices of a regular polygon.
- Example: The solutions x = π/3 + πn/2 on the unit circle represent the vertices of the square.
- Example: The solutions x = π/4 + πn/3 on the unit circle represent the vertices of a regular hexagon.
-
Methods for solving trigonometric equations.
- If a given trigonometric equation contains only one trigonometric function, solve that equation as a basic trigonometric equation. If a given equation includes two or more trigonometric functions, then there are 2 methods for solving such an equation (depending on the possibility of its transformation).
- Method 1.
- Transform this equation into an equation of the form: f(x)*g(x)*h(x) = 0, where f(x), g(x), h(x) are the basic trigonometric equations.
- Example 6. 2cos x + sin 2x = 0. (0< x < 2π)
- Solution. Using the double formula angle sin 2x = 2*sin x*cos x, replace sin 2x.
- 2cos x + 2*sin x*cos x = 2cos x*(sin x + 1) = 0. Now solve the two basic trigonometric equations: cos x = 0 and (sin x + 1) = 0.
- Example 7. cos x + cos 2x + cos 3x = 0. (0< x < 2π)
- Solution: Using trigonometric identities, transform this equation into an equation of the form: cos 2x(2cos x + 1) = 0. Now solve the two basic trigonometric equations: cos 2x = 0 and (2cos x + 1) = 0.
- Example 8. sin x - sin 3x = cos 2x. (0< x < 2π)
- Solution: Using trigonometric identities, transform this equation into an equation of the form: -cos 2x*(2sin x + 1) = 0. Now solve the two basic trigonometric equations: cos 2x = 0 and (2sin x + 1) = 0.
- Method 2.
- Convert the given trigonometric equation into an equation containing only one trigonometric function. Then replace this trigonometric function with some unknown one, for example, t (sin x = t; cos x = t; cos 2x = t, tan x = t; tg (x/2) = t, etc.).
- Example 9. 3sin^2 x - 2cos^2 x = 4sin x + 7 (0< x < 2π).
- Solution. In this equation, replace (cos^2 x) with (1 - sin^2 x) (according to the identity). The transformed equation is:
- 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Replace sin x with t. Now the equation is: 5t^2 - 4t - 9 = 0. This is quadratic equation, having two roots: t1 = -1 and t2 = 9/5. The second root t2 does not satisfy the function range (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
- Example 10. tg x + 2 tg^2 x = ctg x + 2
- Solution. Replace tg x with t. Rewrite the original equation as follows: (2t + 1)(t^2 - 1) = 0. Now find t and then find x for t = tan x.
- If a given trigonometric equation contains only one trigonometric function, solve that equation as a basic trigonometric equation. If a given equation includes two or more trigonometric functions, then there are 2 methods for solving such an equation (depending on the possibility of its transformation).
The relationships between the basic trigonometric functions - sine, cosine, tangent and cotangent - are specified trigonometric formulas. And since there are quite a lot of connections between trigonometric functions, this explains the abundance of trigonometric formulas. Some formulas connect trigonometric functions of the same angle, others - functions of a multiple angle, others - allow you to reduce the degree, fourth - express all functions through the tangent of a half angle, etc.
In this article we will list in order all the basic trigonometric formulas, which are sufficient to solve the vast majority of trigonometry problems. For ease of memorization and use, we will group them by purpose and enter them into tables.
Page navigation.
Basic trigonometric identities
Basic trigonometric identities define the relationship between sine, cosine, tangent and cotangent of one angle. They follow from the definition of sine, cosine, tangent and cotangent, as well as the concept of the unit circle. They allow you to express one trigonometric function in terms of any other.
For a detailed description of these trigonometry formulas, their derivation and examples of application, see the article.
Reduction formulas


Reduction formulas follow from the properties of sine, cosine, tangent and cotangent, that is, they reflect the property of periodicity of trigonometric functions, the property of symmetry, as well as the property of shift by a given angle. These trigonometric formulas allow you to move from working with arbitrary angles to working with angles ranging from zero to 90 degrees.
The rationale for these formulas, a mnemonic rule for memorizing them and examples of their application can be studied in the article.
Addition formulas

Trigonometric addition formulas show how trigonometric functions of the sum or difference of two angles are expressed in terms of trigonometric functions of those angles. These formulas serve as the basis for deriving the following trigonometric formulas.
Formulas for double, triple, etc. angle


Formulas for double, triple, etc. angle (they are also called multiple angle formulas) show how trigonometric functions of double, triple, etc. angles () are expressed in terms of trigonometric functions of a single angle. Their derivation is based on addition formulas.
More detailed information is collected in the article formulas for double, triple, etc. angle
Half angle formulas

Half angle formulas show how trigonometric functions of a half angle are expressed in terms of the cosine of a whole angle. These trigonometric formulas follow from the double angle formulas.
Their conclusion and examples of application can be found in the article.
Degree reduction formulas


Trigonometric formulas for reducing degrees are designed to facilitate the transition from natural powers of trigonometric functions to sines and cosines in the first degree, but multiple angles. In other words, they allow you to reduce the powers of trigonometric functions to the first.
Formulas for the sum and difference of trigonometric functions

Main purpose formulas for the sum and difference of trigonometric functions is to go to the product of functions, which is very useful when simplifying trigonometric expressions. These formulas are also widely used in solving trigonometric equations, as they allow you to factor the sum and difference of sines and cosines.
Formulas for the product of sines, cosines and sine by cosine

The transition from the product of trigonometric functions to a sum or difference is carried out using the formulas for the product of sines, cosines and sine by cosine.
Universal trigonometric substitution

We complete our review of the basic formulas of trigonometry with formulas expressing trigonometric functions in terms of the tangent of a half angle. This replacement was called universal trigonometric substitution. Its convenience lies in the fact that all trigonometric functions are expressed rationally in terms of the tangent of a half angle without roots.
References.
- Algebra: Textbook for 9th grade. avg. school/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M.: Education, 1990. - 272 pp.: ill. - ISBN 5-09-002727-7
- Bashmakov M. I. Algebra and the beginnings of analysis: Textbook. for 10-11 grades. avg. school - 3rd ed. - M.: Education, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
- Algebra and the beginning of analysis: Proc. for 10-11 grades. general education institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn and others; Ed. A. N. Kolmogorov. - 14th ed. - M.: Education, 2004. - 384 pp.: ill. - ISBN 5-09-013651-3.
- Gusev V. A., Mordkovich A. G. Mathematics (a manual for those entering technical schools): Proc. allowance.- M.; Higher school, 1984.-351 p., ill.
Copyright by cleverstudents
All rights reserved.
Protected by copyright law. No part of the site, including internal materials and appearance, may be reproduced in any form or used without the prior written permission of the copyright holder.
Trigonometric equations .
The simplest trigonometric equations .
Methods for solving trigonometric equations.
Trigonometric equations. An equation containing an unknown under the sign of the trigonometric function is called trigonometric.
The simplest trigonometric equations.


Methods for solving trigonometric equations. Solving a trigonometric equation consists of two stages: equation transformation to get it simplest type (see above) and solutionthe resulting simplest trigonometric equation. There are seven basic methods for solving trigonometric equations.
1. Algebraic method. This method is well known to us from algebra.
(variable replacement and substitution method).

2. Factorization. Let's look at this method with examples.
Example 1. Solve the equation: sin x+cos x = 1 .
Solution. Let's move all the terms of the equation to the left:
Sin x+cos x – 1 = 0 ,
Let us transform and factorize the expression in
Left side of the equation:

Example 2. Solve the equation: cos 2 x+ sin x cos x = 1.
Solution: cos 2 x+ sin x cos x– sin 2 x– cos 2 x = 0 ,
Sin x cos x– sin 2 x = 0 ,
Sin x· (cos x– sin x ) = 0 ,

Example 3. Solve the equation: cos 2 x–cos 8 x+ cos 6 x = 1.
Solution: cos 2 x+ cos 6 x= 1 + cos 8 x,
2 cos 4 x cos 2 x= 2cos² 4 x ,
Cos 4 x · (cos 2 x– cos 4 x) = 0 ,
Cos 4 x · 2 sin 3 x sin x = 0 ,
1). cos 4 x= 0, 2). sin 3 x= 0, 3). sin x = 0 ,
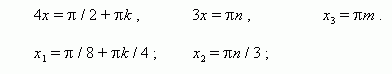
| 3. |
Leading to homogeneous equation. Equation called homogeneous from regarding sin And cos , If all of it members of the same degree relative to sin And cos same angle. To solve a homogeneous equation, you need to: A) move all its members to the left side; b) put all common factors out of brackets; V) equate all factors and brackets to zero; G) parentheses equal to zero give homogeneous equation of lesser degree, which should be divided into cos(or sin) in the senior degree; d) solve the resulting algebraic equation fortan . EXAMPLE Solve equation: 3 sin 2 x+ 4 sin x cos x+ 5cos 2 x = 2. Solution: 3sin 2 x+ 4 sin x cos x+ 5 cos 2 x= 2sin 2 x+ 2cos 2 x , Sin 2 x+ 4 sin x cos x+ 3 cos 2 x = 0 , Tan 2 x+ 4 tan x + 3 = 0 , from here y 2 + 4y +3 = 0 , The roots of this equation are:y 1 = - 1, y 2 = - 3, hence 1) tan x= –1, 2) tan x = –3, |
4. Transition to half angle. Let's look at this method using an example:
EXAMPLE Solve equation: 3 sin x– 5 cos x = 7.
Solution: 6 sin ( x/ 2) cos ( x/ 2) – 5 cos² ( x/ 2) + 5 sin² ( x/ 2) =
7 sin² ( x/ 2) + 7 cos² ( x/ 2) ,
2 sin² ( x/ 2) – 6 sin ( x/ 2) cos ( x/ 2) + 12 cos² ( x/ 2) = 0 ,
tan²( x/ 2) – 3 tan ( x/ 2) + 6 = 0 ,
. . . . . . . . . .
5. Introduction of an auxiliary angle. Consider an equation of the form:
a sin x + b cos x = c ,
Where a, b, c– coefficients;x– unknown.

Now the coefficients of the equation have the properties of sine and cosine, namely: modulus (absolute value) of each








