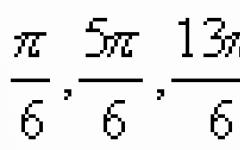Complex numbers. A complex number is a number of the form z=a+biabRi2=−1

Comment.
The real number a is the real part of the number z and is denoted by a=Rez
The real number b is the imaginary part of the number z and is denoted by b=Imz
Real numbers represent a complete set of numbers and operations on them, which, it seems, should be enough to solve any problems in a mathematics course. But how to solve such an equation in real numbers x2+1=0? There is another extension of numbers - complex numbers. In complex numbers, you can take roots from negative numbers.
Algebraic form of a complex number. The algebraic form of a complex number is z=a+bi(aRbRi2=−1)

Comment. If a=ReZ=0b=Imz=0, then the number z is called imaginary. If a=ReZ=0b=Imz=0, then the number z is called purely imaginary

The geometric interpretation of real numbers is the real line. In addition, on the real line “there is no room for new points,” that is, any point on the real axis corresponds to a real number. Consequently, it is no longer possible to place complex numbers on this line, but we can try to consider, along with the real axis on which we will plot the real part of the complex number, another axis perpendicular to it; we will call it the imaginary axis. Then any complex number z = a + ib can be associated with a point in the coordinate plane. We will plot the real part of a complex number on the abscissa axis, and the imaginary part on the ordinate axis. In this way, a one-to-one correspondence is established between all complex numbers and all points of the plane. If such a correspondence is constructed, then the coordinate plane is called a complex plane. The interpretation of the complex number z = a + b i is the vector OA with coordinates (a,b) with the beginning at the point O(0,0) and the end at the point A(a,b)

Conjugate numbers. The numbers z=a+bi and z=a−bi are called conjugate complex numbers

Property. The sum and product of two conjugate complex numbers are real numbers: z+z=2azz=a2+b2

Opposite numbers. The numbers z=a+bi and −z=−a−bi are called opposite complex numbers.

Property. The sum of two opposite complex numbers is zero:
z+(−z)=0

Equal numbers. Two complex numbers are said to be equal if their real and imaginary parts are equal.

Actions with complex numbers given in algebraic form:

Property of addition: The sum of two complex numbers z1=a+bi and z2=c+di will be a complex number of the form z=z1+z2=a+bi+c+di=a+c+(b+d)i
Example: 5+3i+3−i=8+2i

Subtraction property: The difference of two complex numbers z1=a+bi and z2=c+di will be a complex number of the form z=z1−z2=a+bi−c+di=a−c+(b−d)i

Example: . 5+3i−3−i=2+4i

Multiplication property: The product of two complex numbers z1=a+bi and z2=c+di will be a complex number of the form z=z1z2=a+bic+di=ac−bd+(ad+bc)i

Example: 3+2i4−i=12−3i+8i−2i2=14+5i

Division property: The quotient of two complex numbers z1=a+bi and z2=c+di will be a complex number of the form z=z2z1=c+dia+bi=c2+d2ac+bd+c2+d2bc−adi

Example: . 1+i2+i=1+i1−i2+i1−i=1−i22−2i+i−i2=23−21i

Operations with complex numbers given in trigonometric form
Writing a complex number z = a + bi in the form z=rcos+isin is called the trigonometric form of a complex number.

Modulus of a complex number: r=a2+b2

Complex number argument: cos=rasin=rb

Imaginary and complex numbers

Consider the incomplete quadratic equation:
x 2 = a,
where a is a known quantity. The solution to this equation can be written as:
There are three possible cases here:

1). If a = 0, then x = 0.

2). If a is a positive number, then its square root has two values: one positive, the other negative; for example, the equation x 2 = 25 has two roots: 5 and – 5. This is often written as a double root:
3).If a is a negative number, then this equation has no solutions among the positive and negative numbers known to us, because the second power of any number is a non-negative number (think about it!). But if we want to obtain solutions to the equation x 2 = a also for negative values ​​of a, we are forced to introduce numbers of a new type - imaginary numbers. Thus, a number whose second power is a negative number is called imaginary. According to this definition of imaginary numbers, we can also define an imaginary unit:
Then for the equation x 2 = – 25 we get two imaginary roots:
Substituting both of these roots into our equation, we obtain the identity. (Check!). Unlike imaginary numbers, all other numbers (positive and negative, integers and fractions, rational and irrational) are called real or real numbers. The sum of a real and an imaginary number is called a complex number and is denoted by:

Where a, b are real numbers, i is an imaginary unit.

Examples of complex numbers: 3 + 4 i, 7 – 13.6 i, 0 + 25 i = 25 i, 2 + i.

Complex numbers are the minimal extension of the set of real numbers we are familiar with. Their fundamental difference is that an element appears that gives -1 when squared, i.e. i, or .

Any complex number consists of two parts: real and imaginary:

Thus, it is clear that the set of real numbers coincides with the set of complex numbers with a zero imaginary part.

The most popular model for the set of complex numbers is the ordinary plane. The first coordinate of each point will be its real part, and the second will be its imaginary part. Then the role of the complex numbers themselves will be vectors with the beginning at the point (0,0).

Operations on complex numbers.

In fact, if we take into account the model of the set of complex numbers, it is intuitively clear that addition (subtraction) and multiplication of two complex numbers are performed in the same way as the corresponding operations on vectors. Moreover, we mean the vector product of vectors, because the result of this operation is again a vector.

1.1 Addition.

(As you can see, this operation corresponds exactly to)

1.2 Subtraction, similarly, is produced according to the following rule:

2. Multiplication.

3. Division.

Defined simply as the inverse operation of multiplication.

Trigonometric form.

The modulus of a complex number z is the following quantity:

,

obviously, this is, again, just the modulus (length) of the vector (a,b).

Most often, the modulus of a complex number is denoted as ρ.

It turns out that

z = ρ(cosφ+isinφ).

The following follows directly from the trigonometric form of writing a complex number: formulas :

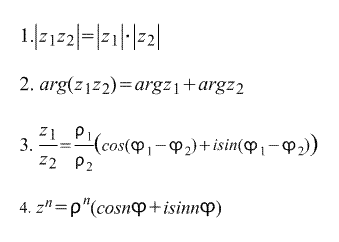
The last formula is called Moivre's formula. The formula is derived directly from it nth root of a complex number:

thus, there are n nth roots of the complex number z.

Example 1

Add two complex numbers,

In order to add two complex numbers, you need to add their real and imaginary parts:

Simple, isn't it? The action is so obvious that it does not require additional comments.

In this simple way you can find the sum of any number of terms: sum the real parts and sum the imaginary parts.

For complex numbers, the first class rule is valid:

– rearranging the terms does not change the sum.

Subtracting Complex Numbers

Example 2

Find the differences of complex numbers and, if,

The action is similar to addition, the only peculiarity is that the subtrahend must be put in brackets, and then the parentheses must be opened in the standard way with a change of sign:

The result should not be confusing; the resulting number has two, not three parts. Simply the real part is the compound: . For clarity, the answer can be rewritten as follows:

Let's calculate the second difference:

Here the real part is also composite:

To avoid any understatement, I will give a short example with a “bad” imaginary part: . Here you can no longer do without parentheses.

Multiplying complex numbers

The time has come to introduce you to the famous equality:

Example 3

Find the product of complex numbers,

Obviously, the work should be written like this:

What does this suggest? It begs to open the brackets according to the rule of multiplication of polynomials. That's what you need to do! All algebraic operations are familiar to you, the main thing is to remember that and be careful.

Let us repeat the school rule for multiplying polynomials: To multiply a polynomial by a polynomial, you need to multiply each term of one polynomial by each term of another polynomial.

I'll write it down in detail:

I hope it was clear to everyone that

Attention, and again attention, most often mistakes are made in signs.

Like the sum, the product of complex numbers is commutable, that is, the equality is true: .

In educational literature and on the Internet, it is easy to find a special formula for calculating the product of complex numbers. Use it if you want, but it seems to me that the approach with multiplying polynomials is more universal and clearer. I won’t give the formula; I think that in this case it’s filling your head with sawdust.

Division of complex numbers

Example 4

Complex numbers are given. Find the quotient.

Let's make a quotient:

The division of numbers is carried out by multiplying the denominator and numerator by the conjugate expression of the denominator.

Let's remember the bearded formula and look at our denominator: . The denominator already has, so the conjugate expression in this case is, that is

According to the rule, the denominator must be multiplied by , and, so that nothing changes, the numerator must be multiplied by the same number:

I'll write it down in detail:

In some cases, before dividing a fraction, it is advisable to simplify it, for example, consider the quotient of numbers: . Before dividing, we get rid of unnecessary minuses: in the numerator and denominator we take the minuses out of brackets and reduce these minuses: . For those who like to solve problems, here is the correct answer:

Rarely, but the following task occurs:

Example 5

The technique is the same - we multiply the denominator and numerator by the conjugate. Given a complex number. Write the given number in algebraic form (i.e., form).

denominator expression. Let's look at the formula again. The denominator already exists, so the denominator and numerator must be multiplied by the conjugate expression, that is, by:

Example 6

Given two complex numbers,. Find their sum, difference, product and quotient.

SubjectComplex numbers and polynomials

Lecture 22

§1. Complex numbers: basic definitions

Symbol is introduced by the ratio
and is called the imaginary unit. In other words,
.

Definition. Expression of the form
, Where
, is called a complex number, and the number called the real part of a complex number and denote
, number – imaginary part and denote
.

From this definition it follows that real numbers are those complex numbers whose imaginary part is equal to zero.

It is convenient to represent complex numbers by points of a plane on which a Cartesian rectangular coordinate system is given, namely: a complex number
corresponds to a point
and vice versa. On axis
real numbers are depicted and it is called the real axis. Complex numbers of the form

are called purely imaginary. They are represented by points on the axis
, which is called the imaginary axis. This plane, which serves to represent complex numbers, is called the complex plane. A complex number that is not real, i.e. such that
, sometimes called imaginary.

Two complex numbers are said to be equal if and only if both their real and imaginary parts are the same.

Addition, subtraction and multiplication of complex numbers is carried out according to the usual rules of polynomial algebra, taking into account the fact that

. The division operation can be defined as the inverse of the multiplication operation and the uniqueness of the result can be proven (if the divisor is non-zero). However, in practice a different approach is used.

Complex numbers
And
are called conjugate; on the complex plane they are represented by points symmetrical about the real axis. It is obvious that:

1)

;

2)
;

3)
.

Now split on can be done as follows:

.

It's not difficult to show that

,

where is the symbol stands for any arithmetic operation.

Let
some imaginary number, and – real variable. Product of two binomials

is a quadratic trinomial with real coefficients.

Now, having complex numbers at our disposal, we can solve any quadratic equation
.If , then

and the equation has two complex conjugate roots

.

If
, then the equation has two different real roots. If
, then the equation has two identical roots.

§2. Trigonometric form of a complex number

As mentioned above, a complex number
convenient to represent as a dot
. This number can also be identified with the radius vector of this point
. With this interpretation, addition and subtraction of complex numbers is carried out according to the rules for addition and subtraction of vectors. For multiplying and dividing complex numbers, another form is more convenient.

Let us introduce on the complex plane
polar coordinate system. Then where
,
and complex number
can be written as:

This form of notation is called trigonometric (in contrast to the algebraic form
). In this form the number is called a module, and – argument of a complex number . They are designated:
,

. For the module we have the formula

The argument of a number is not uniquely defined, but up to a term
,
. The value of the argument satisfying the inequalities
, is called the main one and is denoted
. Then,
. For the main value of the argument, you can get the following expressions:

,

number argument
is considered uncertain.

The condition for the equality of two complex numbers in trigonometric form has the form: the modules of the numbers are equal, and the arguments differ by a multiple of
.

Let's find the product of two complex numbers in trigonometric form:

So, when numbers are multiplied, their modules are multiplied and their arguments are added.

In a similar way, we can establish that when dividing, the modules of numbers are divided and the arguments are subtracted.

Understanding exponentiation as repeated multiplication, we can obtain a formula for raising a complex number to a power:

Let us derive a formula for
– root -th power of a complex number (not to be confused with the arithmetic root of a real number!). The operation of extracting the root is the inverse of the operation of exponentiation. That's why
is a complex number such that
.

Let
is known, but
required to be found. Then

From the equality of two complex numbers in trigonometric form it follows that

,
,
.

From here
(this is an arithmetic root!),

,
.

It is easy to verify that can only accept essentially different values, for example, when
. Finally we have the formula:

,
.

So the root the th power of a complex number has different meanings. On the complex plane, these values ​​are located correctly at the vertices -a triangle inscribed in a circle of radius
with center at the origin. The “first” root has an argument
, the arguments of two “neighboring” roots differ by
.

Example. Let's take the cube root of the imaginary unit:
,
,
. Then:

,