The movement of a point along a circle can be characterized by the angle of rotation of the radius connecting the moving point to the center of the circle. The change in this angle over time is characterized by angular velocity. The angular velocity of a point is the ratio of the angle of rotation of the radius vector of the point to the period of time during which this rotation occurred. Angular velocity is numerically equal to the angle of rotation of the radius vector of a point per unit time.
The angle of rotation is usually measured in radians (rad). The unit of angular velocity is radian per second (rad/s) - the angular velocity at which a point describes an arc based on an angle equal to one radian in one second.
A complete revolution around a circle is rad. This means that if a point rotates with frequency , then its angular velocity is
If the motion of a point along a circle is uneven, then we can introduce the concept of average angular velocity and instantaneous angular velocity, as was done for ordinary speed in the case of uneven motion. In the future, however, we will consider only uniform motion along a circle.
“Ordinary” speed, in contrast to angular speed, will be called linear speed. It is easy to find the relationship between the linear speed of a point, its angular speed and the radius of the circle along which it moves. Since, having described an angle equal to one radian, the point will travel a distance along the circle equal to the radius, then
that is, the linear speed when moving in a circle is equal to the angular speed multiplied by the radius of the circle.
Using (115.1), we can express the centripetal acceleration of a point when moving in a circle in terms of angular velocity. Substituting the expression for speed (115.1) into (27.1), we find a formula expressing centripetal acceleration in terms of angular velocity!
When considering the rotation of a rigid body around an axis, the concept of angular velocity is also used; in this case, the angular velocity of all points of the body is the same, since they all rotate through the same angle. Thus, the rotation of a rigid body around an axis can be characterized by the angular velocity with which all its points move. Therefore, we will call it the angular velocity of the body. From formulas (115.1) and (115.2) it is clear that when a rigid body rotates, the linear velocities of its points and their centripetal accelerations are proportional to the distance from these points to the axis of rotation.
115.1 . Two points move with equal angular velocities along circles whose radii are in the ratio 1:2. Find the ratio of the accelerations of these points.
115.2. What is greater: the angular speed of rotation of the clock hand of a clock or the angular speed of rotation of the Earth?
The distance and the time it takes to cover this distance are connected by a physical concept - speed. And a person, as a rule, does not have any questions about determining this value. Everyone understands that driving a car at a speed of 100 km/h means driving 100 kilometers in one hour.
But what if the body rotates? For example, an ordinary household fan makes tens of revolutions per second. And at the same time, the speed of rotation of the blades is such that they can easily be stopped by hand without harm to yourself. The Earth around its star - the Sun - makes one revolution in a whole year, which is more than 30 million seconds, but the speed of its movement in circumstellar orbit is about 30 kilometers per second!
How to connect the usual speed with the speed of rotation, what does the formula for angular speed look like?
The concept of angular velocity
The concept of angular velocity is used in the study of the laws of rotation. It applies to all rotating bodies. Be it the rotation of a certain mass around another, as in the case of the Earth and the Sun, or the rotation of the body itself around the polar axis (the daily rotation of our planet).
The difference between angular velocity and linear velocity is that it records the change in angle, not distance, per unit time. In physics, angular velocity is usually denoted by the letter of the Greek alphabet “omega” - ω.
The classic formula for angular velocity of rotation is considered as follows.

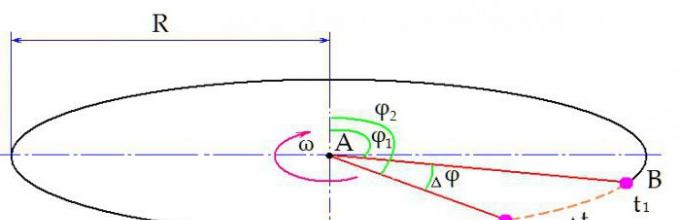
Let's imagine that a physical body rotates around a certain center A at a constant speed. Its position in space relative to the center is determined by the angle φ. At some point in time t1, the body in question is at point B. The angle of deviation of the body from the initial φ1.
Then the body moves to point C. It is there at time t2. Time required for this movement:
The position of the body in space also changes. Now the deflection angle is φ2. The change in angle over the time period ∆t was:
∆φ = φ2 - φ1.
Now the formula for angular velocity is formulated as follows: angular velocity is defined as the ratio of the change in angle ∆φ over time ∆t.
Units of angular velocity
The linear speed of a body is measured in different quantities. The movement of vehicles on roads is usually indicated in kilometers per hour; sea vessels make knots - nautical miles per hour. If we consider the movement of cosmic bodies, then kilometers per second most often appear here.
Angular velocity, depending on the magnitude and the object that is rotating, is also measured in different units.
Radians per second (rad/s) is the classic measure of speed in the International System of Units (SI). They show how many radians (in one full rotation 2 ∙ 3.14 radians) the body manages to turn in one second.
Revolutions per minute (rpm) are the most common unit for indicating rotational speeds in technology. The shafts of both electric and automobile engines produce exactly (just look at the tachometer in your car) revolutions per minute.
Revolutions per second (rps) - used less frequently, primarily for educational purposes.
Circulation period
Sometimes it is more convenient to use another concept to determine the rotation speed. The period of revolution is usually called the time during which a certain body makes a revolution of 360° (a full circle) around the center of rotation. The formula for angular velocity, expressed in terms of the revolution period, takes the form:
Expressing the speed of rotation of bodies by the period of revolution is justified in cases where the body rotates relatively slowly. Let's return to considering the movement of our planet around the star.

The formula for angular velocity allows you to calculate it, knowing the period of revolution:
ω = 2P/31536000 = 0.000000199238499086111 rad/s.
Looking at the result obtained, one can understand why, when considering the rotation of celestial bodies, it is more convenient to use the period of revolution. A person sees clear numbers in front of him and clearly imagines their scale.
Relationship between angular and linear speeds
In some problems, linear and angular velocity must be determined. The transformation formula is simple: the linear velocity of a body is equal to the product of the angular velocity and the radius of rotation. As shown in the picture.

The expression also “works” in the reverse order; with its help, the angular velocity is determined. The formula through linear speed is obtained through simple arithmetic manipulations.
Encyclopedic YouTube
-
1 / 5
In three-dimensional space, the angular velocity vector is equal in magnitude to the angle of rotation of the point around the center of rotation per unit time:
ω = d φ d t , (\displaystyle \omega =(\frac (d\varphi )(dt)),)a is directed along the axis of rotation according to the gimlet rule, that is, in the direction into which a gimlet or a screw with a right-hand thread would be screwed if it rotated in this direction. Another mnemonic for remembering the relationship between the direction of rotation and the direction of the angular velocity vector is that to a conventional observer located at the end of the angular velocity vector emerging from the center of rotation, the rotation itself appears to be occurring against clockwise.
Angular velocity is an axial vector (pseudovector). When the axes of the coordinate system are reflected, the components of a regular vector (for example, the radius vector of a point) change sign. At the same time, the components of the pseudovector (in particular, the angular velocity) with such a coordinate transformation remain the same.
Tensor representation
Units of measurement
Unit of measurement angular velocity, adopted in the International System of Units (SI) and in the GHS and MKGSS systems, - radians per second (Russian designation: rad/s, international: rad/s) . In technology, revolutions per second are also used, much less often - degrees, minutes, seconds of arc per second, degrees per second. Revolutions per minute are often used in technology - this comes from the times when the rotational speed of low-speed steam engines was determined simply by eye, counting the number of revolutions per unit of time.
Properties
The instantaneous velocity vector of any point on an absolutely rigid body rotating with angular velocity is determined by the formula:
v → = [ ω → , r → ] , (\displaystyle (\vec (v))=[\ (\vec (\omega )),(\vec (r))\ ],)where is the radius vector to a given point from the origin located on the axis of rotation of the body, and square brackets denote the vector product. Linear speed (coinciding with the magnitude of the velocity vector) of a point at a certain distance (radius) r (\displaystyle r) from the axis of rotation can be calculated as follows: v = r ω . (\displaystyle v=r\omega .) If other units of measurement of angles are used instead of radians, then in the last two formulas a multiplier will appear that is not equal to one.
- In the case of plane rotation, that is, when all velocity vectors of points of the body always lie in the same plane (“plane of rotation”), the angular velocity of the body is always perpendicular to this plane, and in fact - if the plane of rotation is known - can be replaced by a scalar - a projection onto axis of rotation, that is, on a straight line orthogonal to the plane of rotation. In this case, the kinematics of rotation is greatly simplified. However, in the general case, angular velocity can change direction over time in three-dimensional space, and such a simplified picture does not work.
- Movement with a constant angular velocity vector is called uniform rotational motion (in this case, the angular acceleration is zero). Uniform rotation is a special case of plane rotation.
- The derivative of angular velocity with respect to time is angular acceleration.
- Angular velocity (considered as a free vector) is the same in all inertial reference frames, differing in the position of the reference point and the speed of its movement, but moving uniformly rectilinearly and translationally relative to each other. However, in these inertial reference systems, the position of the axis or center of rotation of the same specific body at the same moment of time may differ (that is, the “point of application” of the angular velocity will be different).
- In the case of a point moving in three-dimensional space, we can write an expression for the angular velocity of this point relative to the selected origin of coordinates:
- In the case of uniform rotational motion (that is, motion with a constant angular velocity vector) of an absolutely rigid body, the Cartesian coordinates of the points of the body rotating in this way make
Rotational motion around a fixed axis is another special case of rigid body motion.
Rotational movement of a rigid body around a fixed axis it is called such a movement in which all points of the body describe circles, the centers of which are on the same straight line, called the axis of rotation, while the planes to which these circles belong are perpendicular rotation axis (Fig.2.4).In technology, this type of motion occurs very often: for example, the rotation of the shafts of engines and generators, turbines and aircraft propellers.
Angular velocity . Each point of a body rotating around an axis passing through the point ABOUT, moves in a circle, and different points travel different paths over time. So, , therefore the modulus of the point velocity A more than a point IN (Fig.2.5). But the radii of the circles rotate through the same angle over time. Angle - the angle between the axis OH and radius vector, which determines the position of point A (see Fig. 2.5).
Let the body rotate uniformly, i.e., rotate through equal angles at any equal intervals of time. The speed of rotation of a body depends on the angle of rotation of the radius vector, which determines the position of one of the points of the rigid body for a given period of time; it is characterized angular velocity . For example, if one body rotates through an angle every second, and the other through an angle, then we say that the first body rotates 2 times faster than the second.
Angular velocity of a body during uniform rotation is a quantity equal to the ratio of the angle of rotation of the body to the period of time during which this rotation occurred.
We will denote the angular velocity by the Greek letter ω (omega). Then by definition
Angular velocity is expressed in radians per second (rad/s).
For example, the angular velocity of the Earth's rotation around its axis is 0.0000727 rad/s, and that of a grinding disk is about 140 rad/s 1 .
Angular velocity can be expressed through rotation speed , i.e. the number of full revolutions in 1s. If a body makes (Greek letter “nu”) revolutions in 1s, then the time of one revolution is equal to seconds. This time is called rotation period and denoted by the letter T. Thus, the relationship between frequency and rotation period can be represented as:A complete rotation of the body corresponds to an angle. Therefore, according to formula (2.1)

If during uniform rotation the angular velocity is known and at the initial moment of time the angle of rotation is , then the angle of rotation of the body during time t according to equation (2.1) is equal to:
If , then , or
 .
.
Angular velocity takes positive values if the angle between the radius vector, which determines the position of one of the points of the rigid body, and the axis OH increases, and negative when it decreases.
Thus, we can describe the position of the points of a rotating body at any time.
Relationship between linear and angular velocities. The speed of a point moving in a circle is often called linear speed , to emphasize its difference from angular velocity.
We have already noted that when a rigid body rotates, its different points have unequal linear velocities, but the angular velocity is the same for all points.
There is a relationship between the linear speed of any point of a rotating body and its angular speed. Let's install it. A point lying on a circle of radius R, will cover the distance in one revolution. Since the time of one revolution of a body is a period T, then the modulus of the linear velocity of the point can be found as follows:Since linear speed uniformly changes direction, the circular motion cannot be called uniform, it is uniformly accelerated.
Angular velocity
Let's choose a point on the circle 1 . Let's build a radius. In a unit of time, the point will move to point 2 . In this case, the radius describes the angle. Angular velocity is numerically equal to the angle of rotation of the radius per unit time.


Period and frequency
Rotation period T- this is the time during which the body makes one revolution.
Rotation frequency is the number of revolutions per second.


Frequency and period are interrelated by the relationship


Relationship with angular velocity


Linear speed
Each point on the circle moves at a certain speed. This speed is called linear. The direction of the linear velocity vector always coincides with the tangent to the circle. For example, sparks from under a grinding machine move, repeating the direction of instantaneous speed.

Consider a point on a circle that makes one revolution, the time spent is the period T. The path that a point travels is the circumference.


Centripetal acceleration
When moving in a circle, the acceleration vector is always perpendicular to the velocity vector, directed towards the center of the circle.



Using the previous formulas, we can derive the following relationships

Points lying on the same straight line emanating from the center of the circle (for example, these could be points that lie on the spokes of a wheel) will have the same angular velocities, period and frequency. That is, they will rotate the same way, but with different linear speeds. The further a point is from the center, the faster it will move.
The law of addition of speeds is also valid for rotational motion. If the motion of a body or frame of reference is not uniform, then the law applies to instantaneous velocities. For example, the speed of a person walking along the edge of a rotating carousel is equal to the vector sum of the linear speed of rotation of the edge of the carousel and the speed of the person.
The Earth participates in two main rotational movements: diurnal (around its axis) and orbital (around the Sun). The period of rotation of the Earth around the Sun is 1 year or 365 days. The Earth rotates around its axis from west to east, the period of this rotation is 1 day or 24 hours. Latitude is the angle between the plane of the equator and the direction from the center of the Earth to a point on its surface.
According to Newton's second law, the cause of any acceleration is force. If a moving body experiences centripetal acceleration, then the nature of the forces that cause this acceleration may be different. For example, if a body moves in a circle on a rope tied to it, then the acting force is the elastic force.

If a body lying on a disk rotates with the disk around its axis, then such a force is the friction force. If the force stops its action, then the body will continue to move in a straight line
Consider the movement of a point on a circle from A to B. The linear speed is equal to v A And vB respectively. Acceleration is the change in speed per unit time. Let's find the difference between the vectors.