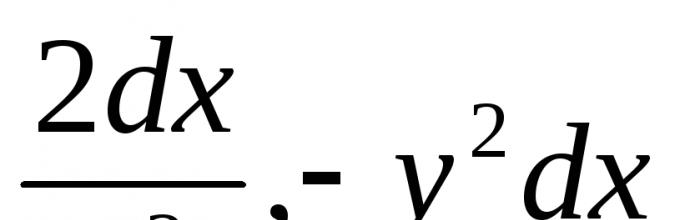Generalized homogeneous equation. Generalized functions corresponding to quadratic forms with complex coefficients Differential equations in generalized functions

Equation M(x, y) dx+ N(x, y) dy=0 is called a generalized homogeneous if it is possible to select such a number k, that the left side of this equation becomes a homogeneous function of some degree m relatively x, y, dx And dy provided that x is considered the value of the first dimension, y – k‑ th measurements , dx And dy – respectively zero and (k-1) th measurements. For example, this would be the equation. (6.1)

Valid under the assumptions made regarding measurements

x, y, dx And dy members of the left side
And dy will have dimensions -2, 2 respectively k And k-1. Equating them, we obtain a condition that the required number must satisfy k: -2 = 2k = k-1. This condition is satisfied when k = -1 (with this k all terms on the left side of the equation under consideration will have a dimension of -2). Consequently, equation (6.1) is generalized homogeneous.

A generalized homogeneous equation is reduced to an equation with separable variables using substitution
, Where z– new unknown function. Let us integrate equation (6.1) using the indicated method. Because k = -1, then
, after which we get the equation.

Integrating it, we find
, where
. This is a general solution to equation (6.1).

§ 7. Linear differential equations of the 1st order.

A 1st order linear equation is an equation that is linear with respect to the desired function and its derivative. It looks like:

, (7.1)

Where P(x) And Q(x) – given continuous functions of x. If the function
, then equation (7.1) has the form:
(7.2)

and is called a linear homogeneous equation, otherwise
it is called a linear inhomogeneous equation.

The linear homogeneous differential equation (7.2) is an equation with separable variables:

(7.3)

Expression (7.3) is the general solution of equation (7.2). To find a general solution to equation (7.1), in which the function P(x) denotes the same function as in equation (7.2), we apply a technique called the method of variation of an arbitrary constant and consists of the following: we will try to select the function C=C(x) so that the general solution to the linear homogeneous equation (7.2) would be a solution to the inhomogeneous linear equation (7.1). Then for the derivative of function (7.3) we obtain:

Substituting the found derivative into equation (7.1), we will have:

or
.

Where
, Where - arbitrary constant. As a result, the general solution to the inhomogeneous linear equation (7.1) will be (7.4)

The first term in this formula represents the general solution (7.3) of the linear homogeneous differential equation (7.2), and the second term of formula (7.4) is a particular solution of the linear inhomogeneous equation (7.1), obtained from the general (7.4) with
. We highlight this important conclusion in the form of a theorem.

Theorem. If one particular solution of a linear inhomogeneous differential equation is known
, then all other solutions have the form
, Where
- general solution of the corresponding linear homogeneous differential equation.

However, it should be noted that to solve the linear inhomogeneous differential equation of the 1st order (7.1), another method is more often used, sometimes called the Bernoulli method. We will look for a solution to equation (7.1) in the form
. Then
. Let's substitute the found derivative into the original equation:
.

Let us combine, for example, the second and third terms of the last expression and extract the function u(x) behind the bracket:
(7.5)

We require the parenthesis to be nullified:
.

Let us solve this equation by setting an arbitrary constant C equal to zero:
. With the found function v(x) Let's return to equation (7.5):
.

Solving it, we get:
.

Consequently, the general solution to equation (7.1) has the form.

.
Differential equations.

§ 1. Basic concepts about ordinary differential equations.

Definition 1. Ordinary differential equation n– th order for the function y argument x is called a relation of the form

Where F– a given function of its arguments. In the name of this class of mathematical equations, the term “differential” emphasizes that they include derivatives
(functions formed as a result of differentiation); the term “ordinary” indicates that the desired function depends on only one real argument.

An ordinary differential equation may not contain an explicit argument x, the required function
and any of its derivatives, but the highest derivative
must be included in the equation n- th order. For example

A)
– first order equation;

b)
– third order equation.

When writing ordinary differential equations, the notation for derivatives in terms of differentials is often used:

V)
– second order equation;

G)
– first order equation,

generator after division by dx equivalent form of specifying the equation:
.

Function
is called a solution to an ordinary differential equation if, upon substitution into it, it turns into an identity.

For example, a 3rd order equation

Has a solution
.

Finding by one method or another, for example, selection, one function that satisfies the equation does not mean solving it. To solve an ordinary differential equation means to find All functions that form an identity when substituted into an equation. For equation (1.1), a family of such functions is formed using arbitrary constants and is called the general solution of an ordinary differential equation n-th order, and the number of constants coincides with the order of the equation: The general solution may be, but is not explicitly resolved with respect to y(x) : In this case, the solution is usually called the general integral of equation (1.1).

For example, the general solution of the differential equation
is the following expression: , and the second term can also be written as
, since an arbitrary constant , divided by 2, can be replaced by a new arbitrary constant .

By assigning some admissible values to all arbitrary constants in the general solution or in the general integral, we obtain a certain function that no longer contains arbitrary constants. This function is called a partial solution or partial integral of equation (1.1). To find the values of arbitrary constants, and therefore a particular solution, various additional conditions to equation (1.1) are used. For example, the so-called initial conditions can be specified at (1.2)

On the right-hand sides of the initial conditions (1.2) the numerical values of the function and derivatives are specified, and the total number of initial conditions is equal to the number of defined arbitrary constants.

The problem of finding a particular solution to equation (1.1) based on the initial conditions is called the Cauchy problem.

§ 2. Ordinary differential equations of the 1st order - basic concepts.

Ordinary differential equation of the 1st order ( n=1) has the form:
or, if it can be resolved with respect to the derivative:
. General solution y= y(x,WITH) or general integral
1st order equations contain one arbitrary constant. The only initial condition for a 1st order equation
allows you to determine the value of a constant from a general solution or from a general integral. Thus, a particular solution will be found or, which is the same, the Cauchy problem will be solved. The question of the existence and uniqueness of a solution to the Cauchy problem is one of the central ones in the general theory of ordinary differential equations. For a 1st order equation, in particular, the theorem is valid, which is accepted here without proof.

Theorem 2.1. If in the equation the function
and its partial derivative
continuous in some region D plane XOY, and in this area a point is specified
, then there is a unique solution that satisfies both the equation and the initial condition
.

Geometrically, the general solution of a 1st order equation is a family of curves on the plane XOY, having no common points and differing from each other in one parameter - the value of the constant C. These curves are called integral curves for a given equation. Integral equation curves have an obvious geometric property: at each point, the tangent of the tangent to the curve is equal to the value of the right side of the equation at this point:
. In other words, the equation is given in the plane XOY field of directions of tangents to integral curves. Comment: It should be noted that to Eq.
the equation and the so-called equation are given in symmetric form
.

§ 3. Differential equations of the 1st order with separable variables.

Definition. A differential equation with separable variables is an equation of the form
(3.1)

or an equation of the form (3.2)

In order to separate the variables in equation (3.1), i.e. reduce this equation to the so-called separated variable equation, do the following:

;

Now we need to solve the equation g(y)= 0 . If it has a real solution y= a, That y= a will also be a solution to equation (3.1).

Equation (3.2) is reduced to a separated variable equation by dividing by the product
:

, which allows us to obtain the general integral of equation (3.2):
. (3.3)

Integral curves (3.3) will be supplemented with solutions
, if such solutions exist.

Solve the equation: .

We separate the variables:

Integrating, we get

Further from the equations
And
we find x=1, y=-1. These solutions are private solutions.

§ 4. Homogeneous differential equations of the 1st order.

Definition 1. A 1st order equation is called homogeneous if for its right side for any
the ratio is valid
, called the condition of homogeneity of a function of two variables of zero dimension.

Example 1. Show that function
- homogeneous zero dimension.

Solution.

Q.E.D.

Theorem. Any function
- homogeneous and, conversely, any homogeneous function
zero dimension is reduced to the form
.

Proof.

The first statement of the theorem is obvious, because
. Let's prove the second statement. Let's put
, then for a homogeneous function
, which was what needed to be proven.

Definition 2. Equation (4.1)

in which M And N– homogeneous functions of the same degree, i.e. have the property for all , is called homogeneous.

Obviously, this equation can always be reduced to the form
(4.2), although to solve it you don’t have to do this.

A homogeneous equation is reduced to an equation with separable variables by replacing the desired function y according to the formula y= zx, Where z(x) – new required function. Having performed this substitution in equation (4.2), we obtain:
or
or
.

Integrating, we obtain the general integral of the equation with respect to the function z(x)
, which after repeated replacement
gives the general integral of the original equation. Moreover, if - roots of the equation
, then the functions
- solving a homogeneous given equation. If
, then equation (4.2) takes the form

and becomes an equation with separable variables. Its solutions are semi-direct:
.

Comment. Sometimes it is advisable to use the substitution instead of the above substitution x= zy.

§ 5. Differential equations reduced to homogeneous ones.

Consider an equation of the form
. (5.1)

If
, then this is the equation using substitution, where And - new variables, and - some constant numbers determined from the system

Reduced to a homogeneous equation

If
, then equation (5.1) takes the form

Believing z= ax+ by, we arrive at an equation that does not contain an independent variable.

Let's look at examples.

Example 1.

Integrate Equation

and highlight the integral curve passing through the points: a) (2;2); b) (1;-1).

Solution.

Let's put y= zx. Then dy= xdz+ zdx And

Let's shorten it by and gather members at dx And dz:

Let's separate the variables:

.

Integrating, we get ;

or
,
.

Replacing here z on , we obtain the general integral of the given equation in the form (5.2)
or

.

This is a family of circles
, whose centers lie on the straight line y = x and which at the origin are tangent to the line y + x = 0. This liney = - x in turn, a particular solution to the equation.

Now the mode of the Cauchy problem:

A) putting in the general integral x=2, y=2, we find C=2, therefore the required solution will be
.

B) none of the circles (5.2) passes through the point (1;-1). But it's semi-straight y = - x,
passes through the point and gives the desired solution.

Example 2. Solve the equation: .

Solution.

The equation is a special case of equation (5.1).

Determinant
in this example
, so we need to solve the following system

Solving, we get that
. By performing a substitution in a given equation
, we obtain a homogeneous equation. Integrating it using substitution
, we find
.

Returning to old variables x And y according to formulas
, we have .

§ 6. Generalized homogeneous equation.

Equation M(x, y) dx+ N(x, y) dy=0 is called generalized homogeneous if it is possible to select such a number k, that the left side of this equation becomes a homogeneous function of some degree m relatively x, y, dx And dy provided that x is considered the value of the first dimension, y – k th measurements , dx And dy – respectively zero and (k-1) th measurements. For example, this would be the equation
. (6.1)

Valid under the assumptions made regarding measurements

x, y, dx And dy members of the left side
And dy will have dimensions -2, 2 respectively k And k-1. Equating them, we obtain a condition that the desired number must satisfy k: -2 = 2k=k-1. This condition is satisfied when k= -1 (with this k all terms on the left side of the equation under consideration will have a dimension of -2). Consequently, equation (6.1) is generalized homogeneous.

Integrating it, we find
, where
. This is a general solution to equation (6.1).

§ 7. Linear differential equations of the 1st order.

A 1st order linear equation is an equation that is linear with respect to the desired function and its derivative. It looks like:

, (7.1)

Where P(x) And Q(x) – given continuous functions of x. If the function
, then equation (7.1) has the form:
(7.2)

and is called a linear homogeneous equation, otherwise
it is called a linear inhomogeneous equation.

The linear homogeneous differential equation (7.2) is an equation with separable variables:

(7.3)

Substituting the found derivative into equation (7.1), we will have:

or
.

Where
, where is an arbitrary constant. As a result, the general solution to the inhomogeneous linear equation (7.1) will be (7.4)

Let us combine, for example, the second and third terms of the last expression and extract the function u(x) behind the bracket:
(7.5)

We require the parenthesis to be nullified:
.

Let us solve this equation by setting an arbitrary constant C equal to zero:
. With the found function v(x) Let's return to equation (7.5):
.

Solving it, we get:
.

Therefore, the general solution to equation (7.1) has the form:

§ 8. Bernoulli's equation.

Definition.

Differential equation of the form
, Where
, is called Bernoulli's equation.

Assuming that
, divide both sides of the Bernoulli equation by . As a result we get:
(8.1)

Let's introduce a new function
. Then
. Let us multiply equation (8.1) by
and let's go to the function z(x) :
, i.e. for function z(x) obtained a linear inhomogeneous equation of the 1st order. This equation is solved using the methods discussed in the previous paragraph. Let us substitute into its general solution instead z(x) expression
, we obtain the general integral of the Bernoulli equation, which is easily resolved with respect to y. At
solution is added y(x)=0 . Bernoulli's equation can also be solved without making the transition to a linear equation by substitution
, and using the Bernoulli method, discussed in detail in § 7. Let's consider the use of this method to solve the Bernoulli equation using a specific example.

Example. Find the general solution to the equation:
(8.2)

Solution.

Therefore, the general solution to this equation has the form:
, y(x)=0.

§ 9. Differential equations in total differentials.

Definition. If in Eq. M(x, y) dx+ N(x, y) dy=0 (9.1) the left side is the total differential of some function U(x, y) , then it is called a total differential equation. This equation can be rewritten as du(x, y)=0 , therefore, its general integral is u(x, y)= c.

For example, the equation xdy+ ydx=0 there is an equation in total differentials, since it can be rewritten in the form d(xy)=0. The general integral will be xy= c- arbitrary differentiable function. Let us differentiate (9.3) with respect to u
§ 10. Integrating factor.

If the equation M(x, y) dx + N(x, y) dy = 0 is not a total differential equation and there is a function µ = µ(x, y) , such that after multiplying both sides of the equation by it, we get the equation

µ(Mdx + Ndy) = 0 in total differentials, i.e. µ(Mdx + Ndy)du, then the function µ(x, y) is called the integrating factor of the equation. In the case where the equation is already an equation in total differentials, we assume µ = 1.

If the integrating factor is found µ , then the integration of this equation is reduced to multiplying both its sides by µ and finding the general integral of the resulting equation in total differentials.

If µ is a continuously differentiable function of x And y, That
.

It follows that the integrating factor µ satisfies the following 1st order partial differential equation:

(10.1).

If it is known in advance that µ= µ(ω) , Where ω – given function from x And y, then equation (10.1) reduces to an ordinary (and, moreover, linear) equation with an unknown function µ on independent variable ω :

(10.2),

Where
, i.e. the fraction is a function only of ω .

Solving equation (10.2), we find the integrating factor

, With = 1.

In particular, the equation M(x, y) dx + N(x, y) dy = 0 has an integrating factor that depends only on x(ω = x) or only from y(ω = y), if the following conditions are met accordingly:

,
.

It is shown how to recognize a generalized homogeneous differential equation. A method for solving a generalized homogeneous differential equation of the first order is considered. An example of a detailed solution of such an equation is given.

Content

Definition

A generalized homogeneous differential equation of the first order is an equation of the form:
, where α ≠ 0 , α ≠ 1 , f - function.

How to Determine Whether a Differential Equation is Generalized Homogeneous

In order to determine whether a differential equation is generalized homogeneous, you need to introduce a constant t and make the substitution:
y → t α · y , x → t · x .
If it is possible to choose a value α at which the constant t decreases, then this is - generalized homogeneous differential equation. The change in derivative y′ with this replacement has the form:
.

Example

Determine whether the given equation is generalized homogeneous:
.

We make the replacement y → t α y, x → t x, y′ → t α- 1 y′:
;
.
Divide by t α+ 5 :
;
.
The equation will not contain t if
4 α - 6 = 0, α = 3/2 .
Since when α = 3/2 , t has decreased, then this is a generalized homogeneous equation.

Solution method

Consider the generalized homogeneous differential equation of the first order:
(1) .
Let us show that it is reduced to a homogeneous equation using substitution:
t = xα.
Really,
.
From here
; .
(1) :
;
.

This is a homogeneous equation. It can be solved by substitution:
y = z t,
where z is a function of t.
When solving problems, it is easier to immediately use substitution:
y = z x α,
where z is a function of x.

An example of solving a generalized homogeneous differential equation of the first order

Solve differential equation
(P.1) .

Let's check whether this equation is generalized homogeneous. For this purpose in (P.1) make a replacement:
y → t α y , x → t x , y′ → t α- 1 y′.
.
Divide by t α:
.
t will be canceled if we set α = - 1 . This means that this is a generalized homogeneous equation.

Let's make a substitution:
y = z x α = z x - 1 ,
where z is a function of x.
.
Substitute into the original equation (P.1):
(P.1) ;
;
.
Multiply by x and open the brackets:
;
;
.
We separate the variables - multiply by dx and divide by x z 2 . When z ≠ 0 we have:
.
We integrate using the table of integrals:
;
;
;
.
Let's potentiate:
.
Let us replace the constant e C → C and remove the modulus sign, since the choice of the desired sign is determined by the choice of the sign of the constant C:
.

Let's return to the variable y. Substitute z = xy:
.
Divide by x:
(P.2) .

When we divided by z 2 , we assumed that z ≠ 0 . Now consider the solution z = xy = 0 , or y = 0 .
Since when y = 0 , left side of the expression (P.2) is not defined, then to the resulting general integral we add the solution y = 0 .

;
.

Used literature:
N.M. Gunther, R.O. Kuzmin, Collection of problems in higher mathematics, “Lan”, 2003.

1st order differential equations with separable variables.

Definition. A differential equation with separable variables is an equation of the form (3.1) or an equation of the form (3.2)

In order to separate the variables in equation (3.1), i.e. reduce this equation to the so-called separated variable equation, do the following: ;

Now we need to solve the equation g(y)= 0. If it has a real solution y=a, That y=a will also be a solution to equation (3.1).

Equation (3.2) is reduced to a separated equation by dividing by the product:

, which allows us to obtain the general integral of equation (3.2): . (3.3)

Integral curves (3.3) will be supplemented with solutions , if such solutions exist.

Homogeneous differential equations of the 1st order.

Definition 1. A first-order equation is called homogeneous if its right-hand side satisfies the relation , called the condition of homogeneity of a function of two variables of zero dimension.

Example 1. Show that the function is homogeneous of zero dimension.

Solution. ,

Q.E.D.

Theorem. Any function is homogeneous and, conversely, any homogeneous function of zero dimension is reduced to the form .

Proof. The first statement of the theorem is obvious, because . Let's prove the second statement. Let us put then for a homogeneous function , which was what needed to be proven.

Definition 2. Equation (4.1) in which M And N– homogeneous functions of the same degree, i.e. have the property for all , called homogeneous. Obviously, this equation can always be reduced to the form (4.2), although this may not be necessary to solve it. A homogeneous equation is reduced to an equation with separable variables by replacing the desired function y according to the formula y=zx, Where z(x)– new required function. Having performed this substitution in equation (4.2), we obtain: or or .

Integrating, we obtain the general integral of the equation with respect to the function z(x) , which after repeated replacement gives the general integral of the original equation. In addition, if are the roots of the equation, then the functions are solutions to a homogeneous given equation. If , then equation (4.2) takes the form

And it becomes an equation with separable variables. Its solutions are half-direct: .

Comment. Sometimes it is advisable to use the substitution instead of the above substitution x=zy.

Generalized homogeneous equation.

Equation M(x,y)dx+N(x,y)dy=0 is called generalized homogeneous if it is possible to select such a number k, that the left side of this equation becomes a homogeneous function of some degree m relatively x, y, dx And dy provided that x is considered the value of the first dimension, y – k‑ th measurements ,dx And dy – respectively zero and (k-1) th measurements. For example, this would be the equation . (6.1) Valid under the assumption made regarding measurements x, y, dx And dy members of the left side and dy will have dimensions -2, 2 respectively k And k-1. Equating them, we obtain a condition that the desired number must satisfy k: -2 = 2k=k-1. This condition is satisfied when k= -1 (with this k all terms on the left side of the equation under consideration will have a dimension of -2). Consequently, equation (6.1) is generalized homogeneous.