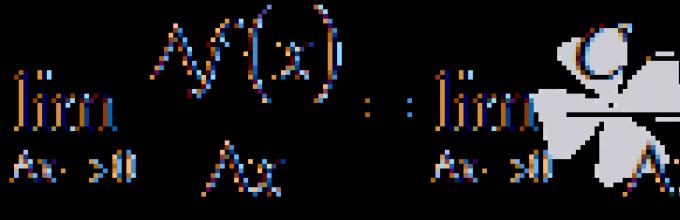When deriving the very first formula of the table, we will proceed from the definition of the derivative function at a point. Let's take where x– any real number, that is, x– any number from the domain of definition of the function. Let us write down the limit of the ratio of the increment of the function to the increment of the argument at : ![]()
It should be noted that under the limit sign the expression is obtained, which is not the uncertainty of zero divided by zero, since the numerator does not contain an infinitesimal value, but precisely zero. In other words, the increment of a constant function is always zero.
Thus, derivative of a constant functionis equal to zero throughout the entire domain of definition.
Derivative of a power function.
The formula for the derivative of a power function has the form ![]() , where the exponent p– any real number.
, where the exponent p– any real number.
Let us first prove the formula for the natural exponent, that is, for p = 1, 2, 3, …
We will use the definition of derivative. Let us write down the limit of the ratio of the increment of a power function to the increment of the argument: 
To simplify the expression in the numerator, we turn to the Newton binomial formula: 
Hence, 
This proves the formula for the derivative of a power function for a natural exponent.
Derivative of an exponential function.
We present the derivation of the derivative formula based on the definition:
We have arrived at uncertainty. To expand it, we introduce a new variable, and at . Then . In the last transition, we used the formula for transitioning to a new logarithmic base.
Let's substitute into the original limit: 
If we recall the second remarkable limit, we arrive at the formula for the derivative of the exponential function: 
Derivative of a logarithmic function.
Let us prove the formula for the derivative of a logarithmic function for all x from the domain of definition and all valid values of the base a logarithm By definition of derivative we have: 
As you noticed, during the proof the transformations were carried out using the properties of the logarithm. Equality  is true due to the second remarkable limit.
is true due to the second remarkable limit.
Derivatives of trigonometric functions.
To derive formulas for derivatives of trigonometric functions, we will have to recall some trigonometry formulas, as well as the first remarkable limit.
By definition of the derivative for the sine function we have ![]() .
.
Let's use the difference of sines formula: 
It remains to turn to the first remarkable limit: 
Thus, the derivative of the function sin x There is cos x.
The formula for the derivative of the cosine is proved in exactly the same way. 
Therefore, the derivative of the function cos x There is –sin x.
We will derive formulas for the table of derivatives for tangent and cotangent using proven rules of differentiation (derivative of a fraction). 
Derivatives of hyperbolic functions.
The rules of differentiation and the formula for the derivative of the exponential function from the table of derivatives allow us to derive formulas for the derivatives of the hyperbolic sine, cosine, tangent and cotangent. 
Derivative of the inverse function.
To avoid confusion during presentation, let's denote in subscript the argument of the function by which differentiation is performed, that is, it is the derivative of the function f(x) By x.
Now let's formulate rule for finding the derivative of an inverse function.
Let the functions y = f(x) And x = g(y) mutually inverse, defined on the intervals and respectively. If at a point there is a finite non-zero derivative of the function f(x), then at the point there is a finite derivative of the inverse function g(y), and ![]() . In another post
. In another post ![]() .
.
This rule can be reformulated for any x from the interval , then we get  .
.
Let's check the validity of these formulas.
Let's find the inverse function for the natural logarithm ![]() (Here y is a function, and x- argument). Having resolved this equation for x, we get (here x is a function, and y– her argument). That is,
(Here y is a function, and x- argument). Having resolved this equation for x, we get (here x is a function, and y– her argument). That is, ![]() and mutually inverse functions.
and mutually inverse functions.
From the table of derivatives we see that ![]() And
And ![]() .
.
Let’s make sure that the formulas for finding the derivatives of the inverse function lead us to the same results: 
Lesson and presentation on the topic: "Number e. Function. Graph. Properties"
Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an anti-virus program.
Teaching aids and simulators in the Integral online store for grade 11
Interactive manual for grades 9–11 "Trigonometry"
Interactive manual for grades 10–11 "Logarithms"
Guys, today we will study a special number. It occupies a separate place in “adult” mathematics and has many remarkable properties, some of which we will consider.
Let's return to the exponential functions $y=a^x$, where $a>1$. We can plot many different function graphs for different bases.
But it should be noted that:
- all functions pass through the point (0;1),
- for $x→-∞$, the graph has a horizontal asymptote $y=0$,
- all functions increase and convex downwards,
- and also continuous, which in turn means that they are differentiable.
Let's consider the function $y=2^x$ and construct a tangent to it.
Having carefully plotted our graphs, you can see that the angle of inclination of the tangent is 35°.
Now let's plot the function $y=3^x$ and also plot the tangent line: 
This time the tangent angle is approximately 48°. In general, it is worth noting: the larger the base exponential function, the greater the angle of inclination.
Of particular interest is the tangent with an angle of inclination equal to 45°. To the graph of which exponential function can such a tangent be drawn at the point (0;1)?
The base of the exponential function must be greater than 2 but less than 3, since the required tangent angle is achieved somewhere between the functions $y=2^x$ and $y=3^x$. Such a number was found and it turned out to be quite unique.
An exponential function in which the tangent passing through the point (0;1) has an angle of inclination equal to 45° is usually denoted by: $y=e^x$ .
The basis of our function is irrational number. Mathematicians have derived the approximate value of this number $e=2.7182818284590…$.
In school mathematics courses, it is customary to round to the nearest tenth, that is, $e=2.7$.
Let's build a graph of the function $y=e^x$ and a tangent to this graph. 
Our function is usually called exponential.
Properties of the function $y=e^x$.
1. $D(f)=(-∞;+∞)$.
2. Is neither even nor odd.
3. Increases throughout the entire domain of definition.
4. Not limited from above, limited from below.
5. Greatest value No, lowest value No.
6. Continuous.
7. $E(f)=(0; +∞)$.
8. Convex downwards.
In higher mathematics it has been proven that an exponential function is differentiable everywhere, and its derivative is equal to the function itself: $(e^x)"=e^x$.
Our function is widely used in many areas of mathematics (in mathematical analysis, in probability theory, in programming), and many real objects are associated with this number.
Example.
Find the tangent to the graph of the function $y=e^x$ at the point $x=2$.
Solution.
The tangent equation is described by the formula: $y=f(a)+f"(a)(x-a)$.
We sequentially find the required values:
1. $f(a)=f(2)=e^2$.
2. $f"(a)=e^a$.
3. $f"(2)=e^2$.
4. $y=f(a)+f"(a)(x-a)=e^2+e^2(x-2)=e^2*x-e^2$.
Answer: $y=e^2*x-e^2$
Example.
Find the value of the derivative of the function $y=e^(3x-15)$ at the point $x=5$.
Solution.
Let's remember the rule for differentiating a function of the form $y=f(kx+m)$.
$y"=k*f"(kx+m)$.
In our case $f(kx+m)=e^(3x-15)$.
Let's find the derivative:
$y"=(e^(3x-15))"=3*e^(3x-15)$.
$y"(5)=3*e^(15-15)=3*e^0=3$.
Answer: 3.
Example.
Examine the function $y=x^3*e^x$ for extrema.
Solution.
Let's find the derivative of our function $y"=(x^3*e^x)"=(x^3)"*e^x+x^3(e^x)"=3x^2*e^x+x^ 3*e^x=x^2*e^x(x+3)$.
The function has no critical points, since the derivative exists for any x.
Equating the derivative to 0, we get two roots: $x_1=0$ and $x_2=-3$.
Let's mark our points on the number line: 
Problems to solve independently
1. Find the tangent to the graph of the function $y=e^(2x)$ at the point $x=2$.2. Find the value of the derivative of the function $y=e^(4x-36)$ at the point $x=9$.
3. Examine the function $y=x^4*e^(2x)$ for extrema.
To use presentation previews, create a Google account and log in to it: https://accounts.google.com
Slide captions:
DERIVATIVE OF AN EXPONENTIAL FUNCTION Number e Grade 11
REPETITION is the mother of learning!
Definition of exponential function Function, given by the formula y = a x (where a > 0, a ≠ 1) is called an exponential function with base a.
Properties of the exponential function y = a x a>1 0
Determination of the derivative of a function at point x 0. as Δ → 0. The derivative of the function f at the point x 0 is the number to which the difference ratio tends as Δx → 0.
Geometric meaning of the derivative x ₀ α A y = f(x) 0 x y к = tan α = f "(x ₀) The angle coefficient to the tangent to the graph of the function f (x) at the point (x 0; f (x 0) is equal to the derivative functions f "(x ₀). f(x 0)
Game: “Find the pairs” (u + v)" cos x e (u v)" n xⁿ ⁻" p (u / v)" - 1 /(sin² x) a (x ⁿ)" - sin x n C "u" v +u v" to (C u)" 1 / (cos ² x) t (sin x)" (u" v – u v") / v² c (cos x)" 0 o (tg x)" u " + v " e (ctg x) " C u " n
Test yourself! (u + v)" u" + v" e (u v)" u" v + u v " to (u /v)" (u' v –u v") / v² s (x ⁿ)" n x ⁿ ⁻¹ p C" 0 o (Cu)" C u " n (sin x)" Cos x e (cos x)" - sin x n (tg x)" 1 / (cos² x) t (ctg x)" - 1 / (sin² x) a
The exponent is power function. An exponent is a function where e is the base of natural logarithms.
1 y= e x 45° The function y= e x is called “exponent” x ₀ =0; tg 45° = 1 At point (0;1) the slope to the tangent to the graph of the function k = tg 45° = 1 - geometric meaning derivative of the exponent Exponent y = e x
Theorem 1. The function y = e is differentiable at each point of the domain of definition, and (e)" = e x x x The natural logarithm (ln) is the logarithm to the base e: ln x = log x e The exponential function is differentiable at each point of the domain of definition, and (a)" = a ∙ ln a x x Theorem 2.
Formulas for differentiating the exponential function (e)" = e ; (e)" = k e ; (a)" = a ∙ ln a; (a)" = k a ∙ ln a. x kx + b x x x kx + b kx + b kx + b F(a x) = + C; F(e x) = e x +C.
“Exercise breeds mastery.” Tacitus Publius Cornelius - ancient Roman historian
Examples: Find the derivatives of the functions: 1. = 3 e. 2. (e)" = (5x)" e = 5 e. 3. (4)" = 4 ln 4. 4. (2)" = (-7 x)" 2 ∙ ln 2 = -7 ∙ 2 ∙ ln 2. 5 x 5 x x (3 e)" 5 x - 7 x x x -7 x -7 x x
Interesting things nearby
Leonhard Euler 1707 -1783 Russian scientist - mathematician, physicist, mechanic, astronomer... Introduced the designation for the number e. Proved that the number e ≈ 2, 718281... is irrational. John Napier 1550 – 1617 Scottish mathematician, inventor of logarithms. In his honor, the number e is called the “Neper number.”
The growth and decay of a function at an exponential rate is called exponential
Lesson objectives: form an idea of number e; prove differentiability of a function at any point X;consider the proof of the theorem on the differentiability of a function; checking the maturity of skills and abilities when solving examples of their application.
Lesson objectives.
Educational: repeat the definition of a derivative, the rules of differentiation, the derivative of elementary functions, remember the graph and properties of an exponential function, develop the ability to find the derivative of an exponential function, test knowledge using a verification task and a test.
Developmental: promote the development of attention, the development of logical thinking, mathematical intuition, the ability to analyze, and apply knowledge in non-standard situations.
Educational: cultivate information culture, develop skills of working in a group and individually.
Teaching methods: verbal, visual, active.
Forms of training: collective, individual, group.
Equipment : textbook “Algebra and the beginnings of analysis” (edited by Kolmogorov), all tasks of group B “Closed segment” edited by A.L. Semenova, I.V. Yashchenko, multimedia projector.
Lesson steps:
- Statement of the topic, purpose, and objectives of the lesson (2 min.).
- Preparation for learning new material by repeating previously learned material (15 min.).
- Introduction to new material (10 min.)
- Initial comprehension and consolidation of new knowledge (15 min.).
- Homework assignment (1 min.).
- Summing up (2 min.).
Lesson progress
1. Organizational moment.
The topic of the lesson is announced: “Derivative of an exponential function. Number e.”, goals, objectives. Slide 1. Presentation
2. Activation of supporting knowledge.
To do this, at the first stage of the lesson we will answer questions and solve repetition problems. Slide 2.
At the board, two students work on cards, completing tasks like B8 Unified State Examination.
Assignment for the first student:
Assignment for the second student:

The rest of the students do independent work according to the following options:
| Option 1 | Option 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Pairs exchange solutions and check each other's work, checking the answers on slide 3.
The solutions and answers of students working at the board are considered.
Examination homework No. 1904. Slide 4 is shown.
3. Updating the topic of the lesson, creating a problem situation.
The teacher asks to define an exponential function and list the properties of the function y = 2 x. Graphs of exponential functions are depicted as smooth lines, to which a tangent can be drawn at each point. But the existence of a tangent to the graph of a function at a point with the abscissa x 0 is equivalent to its differentiability at x 0.
For the graphs of the function y = 2 x and y = 3 x, we draw tangents to them at the point with abscissa 0. The angles of inclination of these tangents to the abscissa axis are approximately equal to 35° and 48°, respectively. Slide 5.
Conclusion: if the base of the exponential function A increases from 2 to, for example, 10, then the angle between the tangent to the graph of the function at the point x = 0 and the abscissa gradually increases from 35° to 66.5°. It is logical to assume that there is a reason A, for which the corresponding angle is 45
It has been proven that there is a number greater than 2 and less than 3. It is usually denoted by the letter e. In mathematics it is established that the number e– irrational, i.e. represents an infinite decimal non-periodic fraction.
e = 2.7182818284590…
Note (not very serious). Slide 6.
On the next slide 7, portraits of great mathematicians appear - John Napier, Leonhard Euler and brief information about them.
- Consider the properties of the function y=e x
- Proof of Theorem 1. Slide 8.
- Proof of Theorem 2. Slide 9.
4. Dynamic pause or relaxation for the eyes.
(Starting position - sitting, each exercise is repeated 3-4 times):
1. Leaning back, take a deep breath, then, leaning forward, exhale.
2. Leaning back in the chair, close your eyelids, close your eyes tightly without opening your eyelids.
3. Arms along the body, circular movements of the shoulders back and forth.
5. Consolidation of the studied material.
5.1 Solution of exercises No. 538, No. 540, No. 544c.
5.2 Independent application of knowledge, skills and abilities. Test work in the form of a test. Task completion time – 5 minutes.
Evaluation criteria:
“5” – 3 points
“4” – 2 points
“3” - 1 point
6. Summing up the results of the work in the lesson.
- Reflection.
- Grading.
- Submission of test tasks.
7. Homework: paragraph 41 (1, 2); No. 539 (a, b, d); 540 (c, d), 544 (a, b).
“Closed segment” No. 1950, 2142.
The graph of an exponential function is a curved, smooth line without kinks, to which a tangent can be drawn at each point through which it passes. It is logical to assume that if a tangent can be drawn, then the function will be differentiable at each point of its domain of definition.
We will display in some coordinate axes several graphs of the function y = x a, For a = 2; a = 2.3; a = 3; a = 3.4.
At a point with coordinates (0;1). The angles of these tangents will be approximately 35, 40, 48 and 51 degrees respectively. It is logical to assume that in the interval from 2 to 3 there is a number at which the angle of inclination of the tangent will be equal to 45 degrees.
Let us give a precise formulation of this statement: there is a number greater than 2 and less than 3, denoted by the letter e, such that the exponential function y = e x at point 0 has a derivative equal to 1. That is: (e ∆x -1) / ∆x tends to 1 as ∆x tends to zero.
This number e is irrational and is written as an infinite non-periodic decimal fraction:
e = 2.7182818284…
Since e is positive and non-zero, there is a logarithm to base e. This logarithm is called natural logarithm . Denoted by ln(x) = log e (x).
Derivative of an exponential function
Theorem: The function e x is differentiable at each point of its domain of definition, and (e x)’ = e x .
The exponential function a x is differentiable at each point of its domain of definition, and (a x)’ = (a x)*ln(a).
A corollary of this theorem is the fact that the exponential function is continuous at any point in its domain of definition.
Example: find the derivative of the function y = 2 x.
Using the formula for the derivative of the exponential function, we obtain:
(2 x)’ = (2 x)*ln(2).
Answer: (2 x)*ln(2).
Antiderivative of the exponential function
For an exponential function a x defined on the set of real numbers, the antiderivative will be the function (a x)/(ln(a)).
ln(a) is some constant, then (a x / ln(a))’= (1 / ln(a)) * (a x) * ln(a) = a x for any x. We have proven this theorem.
Let's consider an example of finding the antiderivative of the exponential function.
Example: find the antiderivative of the function f(x) = 5 x. Let's use the formula given above and the rules for finding antiderivatives. We get: F(x) = (5 x) / (ln(5)) +C.