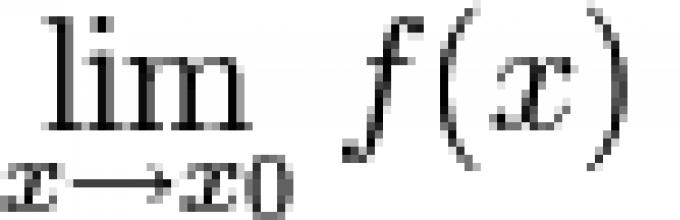Is the function infinitesimal at. Definition of an infinitely large function. Defining a Restricted Sequence

Calculus of infinitesimals and larges

Infinitesimal calculus- calculations performed with infinitesimal quantities, in which the derived result is considered as an infinite sum of infinitesimals. The calculus of infinitesimals is a general concept for differential and integral calculus, which forms the basis of modern higher mathematics. The concept of an infinitesimal quantity is closely related to the concept of limit.

Infinitesimal

Subsequence a n called infinitesimal, If . For example, a sequence of numbers is infinitesimal.

The function is called infinitesimal in the vicinity of a point x 0 if .

The function is called infinitesimal at infinity, If or .

Also infinitesimal is a function that is the difference between a function and its limit, that is, if , That f(x) − a = α( x) , .

Infinitely large quantity

In all the formulas below, infinity to the right of equality is implied to have a certain sign (either “plus” or “minus”). That is, for example, the function x sin x, unbounded on both sides, is not infinitely large at .

Subsequence a n called infinitely large, If .

The function is called infinitely large in the vicinity of a point x 0 if .

The function is called infinitely large at infinity, If or .

Properties of infinitely small and infinitely large

Comparison of infinitesimal quantities

How to compare infinitesimal quantities?
The ratio of infinitesimal quantities forms the so-called uncertainty.

Definitions

Suppose we have infinitesimal values ​​α( x) and β( x) (or, which is not important for the definition, infinitesimal sequences).

To calculate such limits it is convenient to use L'Hopital's rule.

Comparison examples

Using ABOUT-symbolism, the results obtained can be written in the following form x 5 = o(x 3). In this case, the following entries are true: 2x 2 + 6x = O(x) And x = O(2x 2 + 6x).

Equivalent values

Definition

If , then the infinitesimal quantities α and β are called equivalent ().
It is obvious that equivalent quantities are a special case of infinitesimal quantities of the same order of smallness.

When the following equivalence relations are valid (as consequences of the so-called remarkable limits):

Theorem

The limit of the quotient (ratio) of two infinitesimal quantities will not change if one of them (or both) is replaced by an equivalent quantity.

This theorem has practical significance when finding limits (see example).

Usage example

Replacing sin 2x equivalent value 2 x, we get

Historical sketch

The concept of “infinitesimal” was discussed back in ancient times in connection with the concept of indivisible atoms, but was not included in classical mathematics. It was revived again with the advent of the “method of indivisibles” in the 16th century - dividing the figure under study into infinitesimal sections.

In the 17th century, the algebraization of infinitesimal calculus took place. They began to be defined as numerical quantities that are less than any finite (non-zero) quantity and yet not equal to zero. The art of analysis consisted in drawing up a relation containing infinitesimals (differentials) and then integrating it.

Old school mathematicians put the concept to the test infinitesimal harsh criticism. Michel Rolle wrote that the new calculus is “ set of ingenious mistakes"; Voltaire caustically remarked that calculus is the art of calculating and accurately measuring things whose existence cannot be proven. Even Huygens admitted that he did not understand the meaning of differentials of higher orders.

As an irony of fate, one can consider the emergence in the middle of the century of non-standard analysis, which proved that the original point of view - actual infinitesimals - was also consistent and could be used as the basis for analysis.

see also

Wikimedia Foundation. 2010.

See what “Infinitesimal quantity” is in other dictionaries:

INFINITELY SMALL QUANTITY- a variable quantity in a certain process, if in this process it infinitely approaches (tends) to zero... Big Polytechnic Encyclopedia

Infinitesimal- ■ Something unknown, but related to homeopathy... Lexicon of common truths

Function y=f(x) called infinitesimal at x→a or when x→∞, if or , i.e. An infinitesimal function is a function whose limit at a given point is zero.

Examples.

1. Function f(x)=(x-1) 2 is infinitesimal at x→1, since (see figure).

2. Function f(x)= tg x– infinitesimal at x→0.

3. f(x)= log(1+ x) – infinitesimal at x→0.

4. f(x) = 1/x– infinitesimal at x→∞.

Let us establish the following important relationship:

Theorem. If the function y=f(x) representable with x→a as a sum of a constant number b and infinitesimal magnitude α(x): f (x)=b+ α(x) That .

Conversely, if , then f (x)=b+α(x), Where a(x)– infinitesimal at x→a.

Proof.

1. Let us prove the first part of the statement. From equality f(x)=b+α(x) should |f(x) – b|=| α|. But since a(x) is infinitesimal, then for arbitrary ε there is δ – a neighborhood of the point a, in front of everyone x from which, values a(x) satisfy the relation |α(x)|< ε. Then |f(x) – b|< ε. And this means that .

2. If , then for any ε >0 for all X from some δ – neighborhood of a point a will |f(x) – b|< ε. But if we denote f(x) – b= α, That |α(x)|< ε, which means that a– infinitesimal.

Let's consider the basic properties of infinitesimal functions.

Theorem 1. The algebraic sum of two, three, and in general any finite number of infinitesimals is an infinitesimal function.

Proof. Let us give a proof for two terms. Let f(x)=α(x)+β(x), where and . We need to prove that for arbitrary arbitrarily small ε > 0 found δ> 0, such that for x, satisfying the inequality |x – a|<δ , performed |f(x)|< ε.

So, let’s fix an arbitrary number ε > 0. Since according to the conditions of the theorem α(x) is an infinitesimal function, then there is such δ 1 > 0, which is |x – a|< δ 1 we have |α(x)|< ε / 2. Likewise, since β(x) is infinitesimal, then there is such δ 2 > 0, which is |x – a|< δ 2 we have | β(x)|< ε / 2.

Let's take δ=min(δ 1 , δ2 } .Then in the vicinity of the point a radius δ each of the inequalities will be satisfied |α(x)|< ε / 2 and | β(x)|< ε / 2. Therefore, in this neighborhood there will be

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

those. |f(x)|< ε, which is what needed to be proved.

Theorem 2. Product of an infinitesimal function a(x) for a limited function f(x) at x→a(or when x→∞) is an infinitesimal function.

Proof. Since the function f(x) is limited, then there is a number M such that for all values x from some neighborhood of a point a|f(x)|≤M. Moreover, since a(x) is an infinitesimal function at x→a, then for an arbitrary ε > 0 there is a neighborhood of the point a, in which the inequality will hold |α(x)|< ε /M. Then in the smaller of these neighborhoods we have | αf|< ε /M= ε. And this means that af– infinitesimal. For the occasion x→∞ the proof is carried out similarly.

From the proven theorem it follows:

Corollary 1. If and, then.

Corollary 2. If c= const, then .

Theorem 3. Ratio of an infinitesimal function α(x) per function f(x), the limit of which is different from zero, is an infinitesimal function.

Proof. Let . Then 1 /f(x) there is a limited function. Therefore, a fraction is the product of an infinitesimal function and a limited function, i.e. function is infinitesimal.

Def: The function is called infinitesimal at , if .

In the notation “ ” we will assume that x 0 can take as final value: x 0= Сonst, and infinite: x 0= ∞.

Properties of infinitesimal functions:

1) The algebraic sum of a finite number of infinitesimal functions is an infinitesimal sum of functions.

2) The product of a finite number of infinitesimal functions is an infinitesimal function.

3) The product of a bounded function and an infinitesimal function is an infinitesimal function.

4) The quotient of dividing an infinitesimal function by a function whose limit is nonzero is an infinitesimal function.

Example: Function y = 2 + x is infinitesimal at , because .

Def: The function is called infinitely large at , if .

Properties of infinitely large functions:

1) The sum of infinitely large functions is an infinitely large function.

2) The product of an infinitely large function and a function whose limit is nonzero is an infinitely large function.

3) The sum of an infinitely large function and a bounded function is an infinitely large function.

4) The quotient of dividing an infinitely large function by a function that has a finite limit is an infinitely large function.

Example: Function y= is infinitely large at , because .

Theorem.Relationship between infinitely small and infinitely large quantities. If a function is infinitesimal at , then the function is infinitely large at . And conversely, if a function is infinitely large at , then the function is infinitesimal at .

The ratio of two infinitesimals is usually denoted by the symbol, and the ratio of two infinitesimals by the symbol. Both relations are indefinite in the sense that their limit may or may not exist, be equal to a certain number or be infinite, depending on the type of specific functions included in the indefinite expressions.

In addition to uncertainties of type and uncertainties, the following expressions are:

Difference of infinitely large ones of the same sign;

The product of an infinitesimal by an infinitely large;

An exponential function whose base tends to 1 and exponent tends to ;

An exponential function whose base is infinitesimal and whose exponent is infinitely large;

An exponential function whose base and exponent are infinitesimal;

An exponential function whose base is infinitely large and whose exponent is infinitesimal.

It is said that there is uncertainty of the corresponding type. The limit calculation is called in these cases revealing uncertainty. To reveal uncertainty, the expression under the limit sign is converted to a form that does not contain uncertainty.

When calculating limits, the properties of limits are used, as well as the properties of infinitesimal and infinitely large functions.

Let's look at examples of calculations of various limits.

1) . 2) .

4) , because product of an infinitesimal function at and a bounded function is infinitesimal.

5) . 6) .

7) = =

. In this case, there was an uncertainty of type, which was resolved by factoring the polynomials and reducing them to a common factor.

= .

In this case, there was an uncertainty of type , which was resolved by multiplying the numerator and denominator by the expression, using the formula, and then reducing the fraction by (+1).

9)
. In this example, type uncertainty was revealed by dividing the numerator and denominator of the fraction by the leading power.

Wonderful Limits

The first wonderful limit : .

Proof. Let's consider the unit circle (Fig. 3).

Fig.3. Unit circle

Let X– radian measure of the central angle MOA(), Then OA = R= 1, MK= sin x, AT= tg x. Comparing the areas of triangles OMA, OTA and sectors OMA, we get:

,

.

Divide the last inequality by sin x, we get:

.

Since at , then by property 5) limits

This is where the inverse value comes from, which is what needed to be proven.

Comment: If the function is infinitesimal at , i.e. , then the first remarkable limit has the form:

.

Let's look at examples of limit calculations using the first remarkable limit.

When calculating this limit, we used the trigonometric formula: .

.

Let's look at examples of limit calculations using the second remarkable limit.

2) .

3) . There is type uncertainty. Let's make a replacement, then; at .

Calculus of infinitesimals and larges

Infinitesimal calculus- calculations performed with infinitesimal quantities, in which the derived result is considered as an infinite sum of infinitesimals. The calculus of infinitesimals is a general concept for differential and integral calculus, which forms the basis of modern higher mathematics. The concept of an infinitesimal quantity is closely related to the concept of limit.

Infinitesimal

Subsequence a n called infinitesimal, If . For example, a sequence of numbers is infinitesimal.

The function is called infinitesimal in the vicinity of a point x 0 if .

The function is called infinitesimal at infinity, If or .

Also infinitesimal is a function that is the difference between a function and its limit, that is, if , That f(x) − a = α( x) , .

Infinitely large quantity

Subsequence a n called infinitely large, If .

The function is called infinitely large in the vicinity of a point x 0 if .

The function is called infinitely large at infinity, If or .

In all cases, infinity to the right of equality is implied to have a certain sign (either “plus” or “minus”). That is, for example, the function x sin x is not infinitely large at .

Properties of infinitely small and infinitely large

Comparison of infinitesimal quantities

How to compare infinitesimal quantities?
The ratio of infinitesimal quantities forms the so-called uncertainty.

Definitions

Suppose we have infinitesimal values ​​α( x) and β( x) (or, which is not important for the definition, infinitesimal sequences).

To calculate such limits it is convenient to use L'Hopital's rule.

Comparison examples

Using ABOUT-symbolism, the results obtained can be written in the following form x 5 = o(x 3). In this case, the following entries are true: 2x 2 + 6x = O(x) And x = O(2x 2 + 6x).

Equivalent values

Definition

If , then the infinitesimal quantities α and β are called equivalent ().
It is obvious that equivalent quantities are a special case of infinitesimal quantities of the same order of smallness.

When the following equivalence relations are valid: , , .

Theorem

The limit of the quotient (ratio) of two infinitesimal quantities will not change if one of them (or both) is replaced by an equivalent quantity.

This theorem has practical significance when finding limits (see example).

Usage example

Replacing sin 2x equivalent value 2 x, we get

Historical sketch

The concept of “infinitesimal” was discussed back in ancient times in connection with the concept of indivisible atoms, but was not included in classical mathematics. It was revived again with the advent of the “method of indivisibles” in the 16th century - dividing the figure under study into infinitesimal sections.

In the 17th century, the algebraization of infinitesimal calculus took place. They began to be defined as numerical quantities that are less than any finite (non-zero) quantity and yet not equal to zero. The art of analysis consisted in drawing up a relation containing infinitesimals (differentials) and then integrating it.

Old school mathematicians put the concept to the test infinitesimal harsh criticism. Michel Rolle wrote that the new calculus is “ set of ingenious mistakes"; Voltaire caustically remarked that calculus is the art of calculating and accurately measuring things whose existence cannot be proven. Even Huygens admitted that he did not understand the meaning of differentials of higher orders.

As an irony of fate, one can consider the emergence in the middle of the century of non-standard analysis, which proved that the original point of view - actual infinitesimals - was also consistent and could be used as the basis for analysis.

see also

Wikimedia Foundation. 2010.

See what “Infinitely large” is in other dictionaries:

The variable quantity Y is the inverse of the infinitesimal quantity X, that is, Y = 1/X... Big Encyclopedic Dictionary

The variable y is the inverse of the infinitesimal x, that is, y = 1/x. * * * INFINITELY LARGE INFINITELY LARGE, variable quantity Y, inverse to the infinitesimal quantity X, that is, Y = 1/X ... encyclopedic Dictionary

In mathematics, a variable quantity that, in a given process of change, becomes and remains greater in absolute value than any predetermined number. Study of B. b. quantities can be reduced to the study of infinitesimals (See... ... Great Soviet Encyclopedia

The function is called infinitesimal at
or when
, If
or
.

For example: function
infinitesimal at
; function
infinitesimal at
.

Note 1. Without indicating the direction of change of the argument, no function can be called infinitesimal. Yes, the function
at
is infinitesimal, and when
it is no longer infinitesimal (
).

Note 2. From the definition of the limit of a function at a point, for infinitesimal functions the following inequality holds:
We will use this fact more than once in the future.

Let's establish some important properties of infinitesimal functions.

Theorem (about the connection between a function, its limit and the infinitesimal): If the function
can be represented as a sum of a constant number A and infinitesimal function
at
, then the number

Proof:

From the conditions of the theorem it follows that the function
.

Let's express from here
:
. Since the function
infinitesimal, the inequality holds for it
, then for the expression (
) the inequality also holds

And this means that
.

Theorem (reverse): if
, then the function
can be represented as the sum of a number A and infinitesimal at
functions
, i.e.
.

Proof:

Because
, then for
inequality holds
(*) Consider the function
as a single one and rewrite inequality (*) in the form

From the last inequality it follows that the value (
) is infinitesimal at
. Let's denote it
.

Where
. The theorem is proven.

Theorem 1 . The algebraic sum of a finite number of infinitesimal functions is an infinitesimal function.

Proof:

Let us carry out the proof for two terms, since for any finite number of terms it is given in a similar way.

Let
And
infinitesimal at
functions and
– the sum of these functions. Let us prove that for
, there is such a thing
that's for everyone X, satisfying the inequality
, the inequality holds
.

Since the function
infinitesimal function
that's for everyone
inequality holds
.

Since the function
infinitesimal function
, and therefore there is such that's for everyone
inequality holds
.

Let's take equal to the smaller number And , then in –neighborhood of the point A the inequalities will be satisfied
,
.

Let's create a function module
and evaluate its significance.

That is
, then the function is infinitesimal, which is what needed to be proven.

Theorem 2. Product of an infinitesimal function
at
for a limited function
is an infinitesimal function.

Proof:

Since the function
bounded, then there is a positive number
that's for everyone inequality holds
.

Since the function
infinitesimal at
, then there is such –neighborhood of a point that's for everyone in this neighborhood the inequality
.

Consider the function
and evaluate its module

So
, and then
– infinitesimal.

The theorem is proven.

Limit theorems.

Theorem 1. The limit of an algebraic sum of a finite number of functions is equal to the algebraic sum of the limits of these functions

Proof:

To prove it, it is enough to consider two functions; this will not violate the generality of reasoning.

Let
,
.

According to the theorem about the connection between a function, its limit and an infinitesimal function
And
can be represented in the form
Where
And
– infinitesimal at
.

Let's find the sum of functions
And

Magnitude
there is a constant value
– the quantity is infinitesimal. So the function
presented as the sum of a constant value and an infinitesimal function.

Then the number
is the limit of the function
, i.e.

The theorem is proven.

Theorem 2 . The limit of the product of a finite number of functions is equal to the product of the limits of these functions

Proof:

Without losing the generality of reasoning, we will carry out a proof for two functions
And
.

Let it be then
,

Let's find the product of functions
And

Magnitude
there is a constant quantity, an infinitesimal function. Therefore, the number
is the limit of the function
, that is, the equality is true

Consequence:
.

Theorem 3. The limit of the quotient of two functions is equal to the quotient of the limits of these functions if the limit of the denominator is nonzero

.

Proof: Let
,

Then
,
.

Let's find the quotient and perform some identical transformations on it

Magnitude constant, fraction
infinitely small. Therefore, the function represented as the sum of a constant number and an infinitesimal function.

Then
.

Comment. Theorems 1–3 have been proven for the case
. However, they may be applicable when
, since the proof of the theorems in this case is carried out similarly.

For example. Find limits:

The first and second are wonderful limits.

Function not defined at
. However, its values ​​in the vicinity of the zero point exist. Therefore, we can consider the limit of this function at
. This limit is called first wonderful limit .

It looks like:
.

For example . Find limits: 1.
. Designate
, If
, That
.
; 2.
. Let us transform this expression so that the limit is reduced to the first remarkable limit.
; 3..

Let us consider a variable of the form
, wherein takes the values ​​of natural numbers in ascending order. Let's give different meanings: if

Giving the following values ​​from the set
, it is easy to see that the expression
at
will
. Moreover, it is proven that
has a limit. This limit is indicated by the letter :
.

Number irrational:
.

Now consider the limit of the function
at
. This limit is called second remarkable limit

It looks like
.

For example.

A)
. Expression
replace it with the product identical factors
, we apply the product limit theorem and the second remarkable limit; b)
. Let's put
, Then
,
.

The second remarkable limit is used in continuous compounding problem

When calculating cash income on deposits, the compound interest formula is often used, which looks like:

,

Where - initial contribution,

- annual bank interest,

- number of interest accruals per year,

- time, in years.

However, in theoretical studies, when justifying investment decisions, they often use the formula of the exponential (exponential) growth law

.

The formula for the exponential growth law is obtained as a result of applying the second remarkable limit to the compound interest formula

Continuity of functions.

Consider the function
defined at some point and some neighborhood of the point . Let the function have the value at the indicated point
.

Definition 1. Function
called continuous at a point , if it is defined in a neighborhood of a point, including the point itself and
.

The definition of continuity can be formulated differently.

Let the function
defined at some value ,
. If the argument give an increment
, then the function will receive an increment

Let the function at the point continuous (by the first definition of continuity of a function at a point),

That is, if the function is continuous at the point , then an infinitesimal increment of the argument
at this point there corresponds an infinitesimal increment of the function.

The converse is also true: if an infinitesimal increment in the argument corresponds to an infinitesimal increment in the function, then the function is continuous.

Definition 2. Function
is called continuous at
(at point ), if it is defined at this point and some of its surroundings and if
.

Taking into account the first and second definitions of the continuity of a function at a point, we can obtain the following statement:

or
, But
, Then
.

Therefore, in order to find the limit of a continuous function at
it is enough to use an analytical function expression instead of an argument substitute its value .

Definition 3. A function that is continuous at every point of a certain region is called continuous in this area.

For example:

Example 1. Prove that the function
is continuous at all points of the domain of definition.

Let's use the second definition of continuity of a function at a point. To do this, take any value of the argument and give it an increment
. Let's find the corresponding increment of the function

Example 2. Prove that the function
continuous at all points from
.

Let's give the argument increment
, then the function will be incremented

Let's find since the function
, that is, limited.

Similarly, it can be proven that all basic elementary functions are continuous at all points of their domain of definition, that is, the domain of definition of an elementary function coincides with its domain of continuity.

Definition 4. If the function
continuous at every point of some interval
, then we say that the function is continuous on this interval.