A parallelogram is a quadrilateral whose opposite sides are parallel in pairs (Fig. 233).
For an arbitrary parallelogram the following properties hold:
1. Opposite sides of a parallelogram are equal.
Proof. In the parallelogram ABCD we draw the diagonal AC. Triangles ACD and AC B are equal, as having a common side AC and two pairs equal angles, adjacent to it:
(like crosswise angles with parallel lines AD and BC). This means, and like the sides of equal triangles lying opposite equal angles, which is what needed to be proven.

2. Opposite angles of a parallelogram are equal:
3. Adjacent angles of a parallelogram, i.e., angles adjacent to one side, add up, etc.
The proof of properties 2 and 3 is immediately obtained from the properties of angles for parallel lines.
4. The diagonals of a parallelogram bisect each other at their intersection point. In other words,
Proof. Triangles AOD and BOC are congruent, since their sides AD and BC are equal (property 1) and the angles adjacent to them (like crosswise angles for parallel lines). From here it follows that the corresponding sides of these triangles are equal: AO, which is what needed to be proven.
Each of these four properties characterizes a parallelogram, or, as they say, is its characteristic property, i.e., every quadrilateral that has at least one of these properties is a parallelogram (and, therefore, has all the other three properties).
Let us carry out the proof for each property separately.
1". If the opposite sides of a quadrilateral are equal in pairs, then it is a parallelogram.
Proof. Let the quadrilateral ABCD have sides AD and BC, AB and CD respectively equal (Fig. 233). Let's draw the diagonal AC. Triangles ABC and CDA will be congruent as having three pairs of equal sides.
But then the angles BAC and DCA are equal and . The parallelism of sides BC and AD follows from the equality of angles CAD and ACB.
2. If a quadrilateral has two pairs of opposite angles equal, then it is a parallelogram.
Proof. Let . Since then both sides AD and BC are parallel (based on the parallelism of lines).
3. We leave the formulation and proof to the reader.
4. If the diagonals of a quadrilateral bisect each other at the point of intersection, then the quadrilateral is a parallelogram.
Proof. If AO = OS, BO = OD (Fig. 233), then the triangles AOD and BOC are equal, as having equal angles (vertical!) at the vertex O, enclosed between pairs of equal sides AO and CO, BO and DO. From the equality of triangles we conclude that sides AD and BC are equal. The sides AB and CD are also equal, and the quadrilateral turns out to be a parallelogram according to the characteristic property G.
Thus, in order to prove that a given quadrilateral is a parallelogram, it is enough to verify the validity of any of the four properties. The reader is invited to independently prove another characteristic property of a parallelogram.

5. If a quadrilateral has a pair of equal, parallel sides, then it is a parallelogram.
Sometimes any pair of parallel sides of a parallelogram is called its bases, then the other two are called lateral sides. A straight line segment perpendicular to two sides of a parallelogram, enclosed between them, is called the height of the parallelogram. Parallelogram in Fig. 234 has a height h drawn to the sides AD and BC, its second height is represented by the segment .
A parallelogram is a quadrilateral whose opposite sides are parallel, i.e. lie on parallel lines
Properties of a parallelogram: 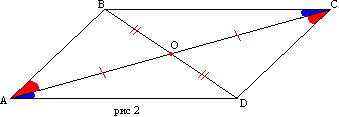 Theorem 22.
Opposite sides of a parallelogram are equal.
Theorem 22.
Opposite sides of a parallelogram are equal.
Proof. In the parallelogram ABCD we draw a diagonal AC. Triangles ACD and ACB are congruent, as having a common side AC and two pairs of equal angles. adjacent to it: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (as crosswise angles with parallel lines AD and BC). This means that AB = CD and BC = AD, as the corresponding sides of equal triangles, etc. The equality of these triangles also implies the equality corresponding angles triangles:
Theorem 23.
The opposite angles of the parallelogram are equal: ∠ A=∠ C and ∠ B=∠ D.
The equality of the first pair comes from the equality of triangles ABD and CBD, and the second - ABC and ACD.
Theorem 24.
Adjacent angles of a parallelogram, i.e. angles adjacent to one side add up to 180 degrees.
This is so because they are interior one-sided angles.
Theorem 25.
The diagonals of a parallelogram bisect each other at their intersection point.
Proof. Consider triangles BOC and AOD. According to the first property AD=BC ∠ OAD=∠ OCB and ∠ ODA=∠ OBC lying crosswise for parallel lines AD and BC. Therefore, triangles BOC and AOD are equal in side and adjacent angles. This means BO=OD and AO=OS, like the corresponding sides of equal triangles, etc.
Signs of a parallelogram
Theorem 26.
If the opposite sides of a quadrilateral are equal in pairs, then it is a parallelogram.
Proof. Let the quadrilateral ABCD have sides AD and BC, AB and CD respectively equal (Fig. 2). Let's draw the diagonal AC. Triangles ABC and ACD are equal on three sides. Then angles BAC and DCA are equal and, therefore, AB is parallel to CD. The parallelism of sides BC and AD follows from the equality of angles CAD and ACB.
Theorem 27.
If the opposite angles of a quadrilateral are equal in pairs, then it is a parallelogram.
Let ∠ A=∠ C and ∠ B=∠ D. Because ∠ A+∠ B+∠ C+∠ D=360 o, then ∠ A+∠ B=180 o and sides AD and BC are parallel (based on the parallelism of straight lines). We will also prove the parallelism of sides AB and CD and conclude that ABCD is a parallelogram by definition.
Theorem 28.
If adjacent corners of a quadrilateral, i.e. The angles adjacent to one side add up to 180 degrees, then it is a parallelogram.
If the interior one-sided angles add up to 180 degrees, then the straight lines are parallel. So AB is parallel to CD and BC is parallel to AD. A quadrilateral turns out to be a parallelogram by definition.
Theorem 29.
If the diagonals of a quadrilateral bisect each other at the point of intersection, then the quadrilateral is a parallelogram.
Proof. If AO = OC, BO = OD, then triangles AOD and BOC are equal, as having equal (vertical) angles at vertex O, enclosed between pairs of equal sides. From the equality of triangles we conclude that AD and BC are equal. The sides AB and CD are also equal, and the quadrilateral turns out to be a parallelogram according to criterion 1.
Theorem 30.
If a quadrilateral has a pair of equal, parallel sides, then it is a parallelogram.
Let the sides AB and CD of quadrilateral ABCD be parallel and equal. Let's draw diagonals AC and BD. From the parallelism of these lines it follows that the crosswise angles ABO = CDO and BAO = OCD are equal. Triangles ABO and CDO are equal in side and adjacent angles. Therefore AO=OS, VO=ОD, i.e. The diagonals are divided in half by the intersection point and the quadrilateral turns out to be a parallelogram according to criterion 4.
In geometry, special cases of parallelograms are considered.
Definition
Parallelogram is a quadrilateral whose opposite sides are parallel in pairs.
The point of intersection of the diagonals of a parallelogram is called center.
Properties of a parallelogram:
- The sum of any two adjacent angles of a parallelogram is $180^(\circ)$, and the opposite angles are equal.
- Opposite sides of a parallelogram are equal.
- The diagonals of a parallelogram intersect and bisect at the point of intersection.
Proof
Let a parallelogram $ABCD$ be given.
1. Note that the adjacent angles $A$ and $B$ of a parallelogram are one-sided interior angles with parallel lines $AD$ and $BC$ and a secant $AB$, that is, their sum is equal to $180^\circ$. Likewise for other pairs of angles.
If $\angle A + \angle B=180^\circ$ and $\angle C + \angle B=180^\circ$, then $\angle A = \angle C$. Similarly, $\angle B = \angle D$.
2. Consider triangles $ABC$ and $CDA$. From the parallelism of opposite sides of a parallelogram it follows that $\angle BAC=\angle DCA$ and $\angle BCA=\angle DAC$. Since $AC$ is common, then the triangles $ABC$ and $CDA$ are equal according to the second criterion. From the equality of triangles it follows that $AB=CD$ and $BC=AD$.
3. Since a parallelogram is convex quadrilateral, then its diagonals intersect. Let $O$ be the intersection point. From the parallelism of the sides $BC$ and $AD$ of the parallelogram it follows that $\angle OAD=\angle OCB$ and $\angle ODA=\angle OBC$. Taking into account the equality $BC=AD$, we obtain that the triangles $AOD$ and $COB$ are equal according to the second criterion. Therefore, $AO=CO$ and $DO=BO$, as required.

Signs of a parallelogram:
- If in a quadrilateral the sum of any two adjacent angles is $180^(\circ)$, then this quadrilateral is a parallelogram.
- If in a quadrilateral the opposite angles are equal in pairs, then this quadrilateral is a parallelogram.
- If in a quadrilateral the opposite sides are equal in pairs, then this quadrilateral is a parallelogram.
- If two sides of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram.
- If the diagonals of a quadrilateral are bisected by their intersection point, then the quadrilateral is a parallelogram.
Proof
Let $ABCD$ be a quadrilateral.
1. Note that adjacent angles $A$ and $B$ are one-sided interior angles with straight lines $AD$ and $BC$ and transversal $AB$. Since their sum is $180^\circ$, then the lines $AD$ and $BC$ are parallel. Similarly for another pair of lines, that is, $ABCD$ is a parallelogram by definition.
2. Note that $\angle A + \angle B + \angle C + \angle D=360^\circ$. If $\angle A = \angle C$, and $\angle B = \angle D$, then $\angle A + \angle B=180^\circ$ and similarly for other pairs of adjacent angles. Next we use the previous sign.
3. Consider triangles $ABC$ and $CDA$. Since $AC$ is common, it follows from the equality of opposite sides of the parallelogram that the triangles $ABC$ and $CDA$ are equal according to the third criterion. Therefore, $\angle BAC=\angle DCA$ and $\angle BCA=\angle DAC$, which implies the parallelism of the opposite sides.
4. Let $BC$ and $AD$ be equal and parallel. Consider triangles $ABC$ and $CDA$. From the parallelism of the lines it follows that $\angle BCA=\angle DAC$. Since $AC$ is general and $BC=AD$, then the triangles $ABC$ and $CDA$ are equal according to the first criterion. Therefore, $AB=CD$. Next we use the previous sign.
5. Let $O$ be the intersection point of the diagonals and $AO=CO$, and $DO=BO$. Taking into account the equality of the vertical angles, we obtain that the triangles $AOD$ and $COB$ are equal according to the first criterion. Therefore, $\angle OAD=\angle OCB$, which implies the parallelism of $BC$ and $AD$. Likewise for the other pair of sides.
Definition
A quadrilateral that has three right angles is called rectangle.
Rectangle properties:
- The diagonals of a rectangle are equal.
Proof
Let a rectangle $ABCD$ be given. Since a rectangle is a parallelogram, its opposite sides are equal. Then right triangles$ABD$ and $DCA$ are equal on two legs, which means that $BD=AC$.
Features of a rectangle:
- If a parallelogram has a right angle, then this parallelogram is a rectangle.
- If the diagonals of a parallelogram are equal, then this parallelogram is a rectangle.
Proof
1. If one of the angles of a parallelogram is straight, then, taking into account that the sum of adjacent angles is $180^(\circ)$, we obtain that the remaining angles are also straight.
2. Let the diagonals $AC$ and $BD$ be equal in the parallelogram $ABCD$. Taking into account the equality of the opposite sides $AB$ and $DC$, we obtain that the triangles $ABD$ and $DCA$ are equal according to the third criterion. Therefore, $\angle BAD=\angle CDA$, that is, they are straight. It remains to use the previous sign.
Definition
A quadrilateral in which all sides are equal is called diamond
Properties of a rhombus:
- The diagonals of a rhombus are mutually perpendicular and are the bisectors of its angles.
Proof
Let the diagonals $AC$ and $BD$ in the rhombus $ABCD$ intersect at the point $O$. Since a rhombus is a parallelogram, $AO=OC$. Let's consider isosceles triangle$ABC$. Since $AO$ is the median drawn to the base, it is the bisector and the height, which is what was required.
Signs of a diamond:
- If the diagonals of a parallelogram are mutually perpendicular, then this parallelogram is a rhombus.
- If the diagonal of a parallelogram is the bisector of its angle, then this parallelogram is a rhombus.
Proof
Let the parallelogram $ABCD$ have diagonals $AC$ and $BD$ intersect at point $O$. Consider triangle $ABC$.
1. If the diagonals are perpendicular, then $BO$ is the median and height of the triangle.
2. If the diagonal $BD$ contains the bisector of the angle $ABC$, then $BO$ is the median and the bisector in the triangle.
In both cases, we find that the triangle $ABC$ is isosceles and in a parallelogram the adjacent sides are equal. Therefore, it is a rhombus, which is what was required.
Definition
A rectangle whose two adjacent sides are equal is called square.
Signs of a square:
- If a rhombus has a right angle, then that rhombus is a square.
- If a rhombus has equal diagonals, then the rhombus is a square.
Proof
If a parallelogram has a right angle or equal diagonals, then it is a rectangle. If a quadrilateral is a rectangle and a rhombus, then it is a square.
A parallelogram is a quadrilateral whose opposite sides are parallel in pairs. The area of a parallelogram is equal to the product of its base (a) and height (h). You can also find its area through two sides and an angle and through diagonals.
Properties of a parallelogram
1. Opposite sides are identical
First of all, let's draw the diagonal \(AC\) . We get two triangles: \(ABC\) and \(ADC\).
Since \(ABCD\) is a parallelogram, the following is true:
\(AD || BC \Rightarrow \angle 1 = \angle 2\) like lying crosswise.
\(AB || CD \Rightarrow \angle3 = \angle 4\) like lying crosswise.
Therefore, (according to the second criterion: and \(AC\) is common).
And that means \(\triangle ABC = \triangle ADC\), then \(AB = CD\) and \(AD = BC\) .
2. Opposite angles are identical

According to the proof properties 1 we know that \(\angle 1 = \angle 2, \angle 3 = \angle 4\). Thus the sum of opposite angles is: \(\angle 1 + \angle 3 = \angle 2 + \angle 4\). Considering that \(\triangle ABC = \triangle ADC\) we get \(\angle A = \angle C \) , \(\angle B = \angle D \) .
3. Diagonals are divided in half by the intersection point

By property 1 we know that opposite sides are identical: \(AB = CD\) . Once again, note the crosswise lying equal angles.
Thus it is clear that \(\triangle AOB = \triangle COD\) according to the second sign of equality of triangles (two angles and the side between them). That is, \(BO = OD\) (opposite the angles \(\angle 2\) and \(\angle 1\) ) and \(AO = OC\) (opposite the angles \(\angle 3\) and \( \angle 4\) respectively).
Signs of a parallelogram
If only one feature is present in your problem, then the figure is a parallelogram and you can use all the properties of this figure.
For better memorization, note that the parallelogram test will answer the following question - “how to find out?”. That is, how do you know what set figure this is a parallelogram.
1. A parallelogram is a quadrilateral whose two sides are equal and parallel
\(AB = CD\) ; \(AB || CD \Rightarrow ABCD\)- parallelogram.

Let's take a closer look. Why \(AD || BC \) ?
\(\triangle ABC = \triangle ADC\) By property 1: \(AB = CD \) , \(\angle 1 = \angle 2 \) lying crosswise when \(AB \) and \(CD \) and the secant \(AC \) are parallel.
But if \(\triangle ABC = \triangle ADC\), then \(\angle 3 = \angle 4 \) (lie opposite \(AD || BC \) (\(\angle 3 \) and \(\angle 4 \) - those lying crosswise are also equal).
The first sign is correct.
2. A parallelogram is a quadrilateral whose opposite sides are equal
\(AB = CD \) , \(AD = BC \Rightarrow ABCD \) is a parallelogram.

Let's consider this sign. Let's draw the diagonal \(AC\) again.
By property 1\(\triangle ABC = \triangle ACD\).
It follows from this that: \(\angle 1 = \angle 2 \Rightarrow AD || BC \) And \(\angle 3 = \angle 4 \Rightarrow AB || CD \), that is, \(ABCD\) is a parallelogram.
The second sign is correct.
3. A parallelogram is a quadrilateral whose opposite angles are equal
\(\angle A = \angle C\) , \(\angle B = \angle D \Rightarrow ABCD\)- parallelogram.

\(2 \alpha + 2 \beta = 360^(\circ) \)(since \(\angle A = \angle C\) , \(\angle B = \angle D\) by condition).
It turns out, . But \(\alpha \) and \(\beta \) are internal one-sided at the secant \(AB \) .
And what \(\alpha + \beta = 180^(\circ) \) also says that \(AD || BC \) .
Proof
First of all, let's draw the diagonal AC. We get two triangles: ABC and ADC.

Since ABCD is a parallelogram, the following is true:
AD || BC \Rightarrow \angle 1 = \angle 2 like lying crosswise.
AB || CD\Rightarrow\angle3 =\angle 4 like lying crosswise.
Therefore, \triangle ABC = \triangle ADC (according to the second criterion: and AC is common).
And, therefore, \triangle ABC = \triangle ADC, then AB = CD and AD = BC.
Proven!
2. Opposite angles are identical.

Proof
According to the proof properties 1 we know that \angle 1 = \angle 2, \angle 3 = \angle 4. Thus the sum of opposite angles is: \angle 1 + \angle 3 = \angle 2 + \angle 4. Considering that \triangle ABC = \triangle ADC we get \angle A = \angle C , \angle B = \angle D .
Proven!
3. The diagonals are divided in half by the intersection point.

Proof
Let's draw another diagonal.

By property 1 we know that opposite sides are identical: AB = CD. Once again, note the crosswise lying equal angles.
Thus, it is clear that \triangle AOB = \triangle COD according to the second criterion for the equality of triangles (two angles and the side between them). That is, BO = OD (opposite the corners \angle 2 and \angle 1) and AO = OC (opposite the corners \angle 3 and \angle 4, respectively).

Proven!
Signs of a parallelogram
If only one feature is present in your problem, then the figure is a parallelogram and you can use all the properties of this figure.
For better memorization, note that the parallelogram sign will answer the following question - “how to find out?”. That is, how to find out that a given figure is a parallelogram.
1. A parallelogram is a quadrilateral whose two sides are equal and parallel.

AB = CD ; AB || CD\Rightarrow ABCD is a parallelogram.
Proof
Let's take a closer look. Why AD || BC?

\triangle ABC = \triangle ADC by property 1: AB = CD, AC - common and \angle 1 = \angle 2 lying crosswise with parallel AB and CD and secant AC.
But if \triangle ABC = \triangle ADC , then \angle 3 = \angle 4 (lie opposite AB and CD, respectively). And therefore AD || BC (\angle 3 and \angle 4 - those lying crosswise are also equal).

The first sign is correct.
2. A parallelogram is a quadrilateral whose opposite sides are equal.

AB = CD, AD = BC \Rightarrow ABCD is a parallelogram.
Proof
Let's consider this sign. Let's draw the diagonal AC again.

By property 1\triangle ABC = \triangle ACD .

It follows from this that: \angle 1 = \angle 2 \Rightarrow AD || B.C. And \angle 3 = \angle 4 \Rightarrow AB || CD, that is, ABCD is a parallelogram.
The second sign is correct.
3. A parallelogram is a quadrilateral whose opposite angles are equal.

\angle A = \angle C , \angle B = \angle D \Rightarrow ABCD- parallelogram.
Proof

2 \alpha + 2 \beta = 360^(\circ)(since ABCD is a quadrilateral, and \angle A = \angle C , \angle B = \angle D by condition).
It turns out that \alpha + \beta = 180^(\circ) . But \alpha and \beta are internal one-sided at the secant AB.
And the fact that \alpha + \beta = 180^(\circ) also means that AD || B.C.
Moreover, \alpha and \beta are internal one-sided at the secant AD . And that means AB || CD.
The third sign is correct.
4. A parallelogram is a quadrilateral whose diagonals are divided in half by the point of intersection.

AO = OC ; BO = OD\Rightarrow parallelogram.
Proof

BO = OD; AO = OC , \angle 1 = \angle 2 as vertical \Rightarrow \triangle AOB = \triangle COD, \Rightarrow \angle 3 = \angle 4, and \Rightarrow AB || CD.
Similarly BO = OD; AO = OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8, and \Rightarrow AD || B.C.
The fourth sign is correct.







