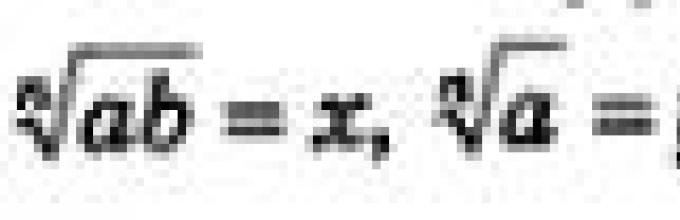It is necessary to get acquainted with the properties of this operation, which we will do in this section.
All properties are formulated and proved only for non-negative values of the variables contained under the signs of the roots.
Evidence. Let us introduce the following notation: ![]() We need to prove that the equality x-yz holds for non-negative numbers x, y, z.
We need to prove that the equality x-yz holds for non-negative numbers x, y, z.
As
So, But if the degrees of two non-negative numbers are equal and the exponents are equal, then the bases are also equal degrees; hence, from the equality x n = (yz) n it follows that x-yz, and this is what was required to prove.
Here is a short summary of the proof of the theorem.

Notes:
1.
Theorem 1 remains valid for the case when the radical expression is the product of more than two non-negative numbers.
2.
Theorem 1 can be formulated using the construction "if ... then" (as is customary for theorems in mathematics.) Let us give the corresponding formulation: if a and b are non-negative numbers, then the equality holds.

A short (albeit imprecise) formulation that is more convenient to use in practice: the root of fractions is equal to the fraction of the roots.
Evidence. Here is a short summary of the proof of Theorem 2, and you try to make the appropriate comments, similar to those given in the proof of Theorem 1.

YOU, of course, have noticed that the proven two properties of the roots nth degree are a generalization of the properties of square roots known to you from the course of 8th grade algebra. And if other properties roots nth degree was not, then how would it be simple (and not very interesting). There are actually a few more interesting and important properties that we will discuss in this section. But first, consider a few examples of using Theorems 1 and 2.
Example 1. Calculate
Decision. Using the first property of roots (Theorem 1), we get:
Remark 3. You can, of course, solve this example differently, especially if you have a calculator at hand: multiply the numbers 125, 64 and 27, and then extract the cube root from the resulting product. But, you see, the proposed solution is "more intelligent".
Example 2. Calculate
Decision. Let us turn mixed number into an improper fraction.
We have Using the second property of the roots (Theorem 2), we obtain:
![]()
Example 3. Calculate: ![]()
Decision. Any formula in algebra, as you well know, is used not only "from left to right", but also "from right to left". So, the first property of roots means that it can be represented in the form and, conversely, can be replaced by an expression. The same applies to the second property of roots. With this in mind, let's perform the calculations:
Example 4. Follow the steps:
Decision, a) We have:
b) Theorem 1 allows us to multiply only roots of the same degree, i.e. only roots with the same index. Here it is proposed to multiply the root of the 2nd degree of the number a by the root of the 3rd degree of the same number. We do not yet know how to do this. We will return to this problem later.
Let's continue our study of the properties of radicals.
In other words, to raise a root to a natural degree, it is enough to raise a radical expression to this degree.
This is a consequence of Theorem 1. Indeed, for example, for k = 3 we obtain: In the same way, one can reason in the case of any other natural value of the exponent k.
In other words, to extract a root from a root, it is enough to multiply the indices of the roots.
For example,
Evidence. As in Theorem 2, here is a short summary of the proof, and you try to make the appropriate comments yourself, similar to those given in the proof of Theorem 1.

Remark 4. Let's take a breath. What have we learned from the proven theorems? We learned that four operations can be performed on roots: multiplication, division, exponentiation, and root extraction (from the root). But what about the addition and subtraction of roots? No way. We talked about this back in the 8th grade about the operation of extracting a square root.
For example, instead of it is impossible to write Indeed, But it is obvious that Be careful!
Perhaps the most interesting property of roots is the one that will be discussed in the next theorem. Given the special importance of this property, we will allow ourselves to violate the certain style of formulations and proofs developed in this section, so that the formulation of Theorem 5 is a little "softer" and its proof is clearer.
For example:
(indicators of the root and radical expression were divided by 4);
(indicators of the root and radical expression were divided by 3);
(the indicators of the root and radical expression were multiplied by 2).
Evidence. Let us denote the left-hand side of the equality being proved by the letter Then, by the definition of the root, the equality
Let us denote the right-hand side of the identity being proved by the letter y:
Then, by the definition of the root, the equality
Let us raise both sides of the last equality to the same power p; we get:
So (see equalities (1) and (2)),
![]()
Comparing these two equalities, we come to the conclusion that x np = y np, and therefore x = y, which was required to prove.
The proved theorem will allow us to solve the problem that we encountered above when solving Example 5, where it was required to perform multiplication of roots with different exponents:
This is how one usually thinks in such cases.
1) By Theorem 5, in the expression, you can multiply both the exponent of the root (i.e., the number 2) and the exponent of the radical expression (i.e., the number 1) by the same natural number... Taking advantage of this, we multiply both indicators by 3; we get:
2) According to Theorem 5, in the expression, it is possible to multiply both the exponent of the root (i.e., the number 3) and the exponent of the radical expression (i.e., the number 1) by the same natural number. Taking advantage of this, we multiply both indicators by 2; we get:
3) Since we got the roots of the same 6th degree, we can multiply them:
Remark 5. Have you forgotten that all the properties of the roots that we discussed in this paragraph were considered by us only for the case when the variables take only non-negative values? Why did you have to make such a restriction? Because root nth degrees from negative number does not always make sense - it is defined only for odd values of n. For such values of the root exponent, the considered properties of the roots are also true in the case of negative radical expressions.
A.G. Mordkovich Algebra Grade 10
Lesson content lesson outline support frame lesson presentation accelerative methods interactive technologies Practice tasks and exercises self-test workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photos, pictures, charts, tables, schemes humor, anecdotes, jokes, comics parables, sayings, crosswords, quotes Add-ons abstracts articles chips for the curious cheat sheets textbooks basic and additional vocabulary of terms others Improving textbooks and lessonsbug fixes in the tutorial updating a fragment in the textbook elements of innovation in the lesson replacing outdated knowledge with new ones For teachers only perfect lessons calendar plan for a year guidelines discussion agenda Integrated lessonsYour privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please read our privacy policy and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify a specific person or contact him.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information we collect:
- When you leave a request on the site, we may collect various information, including your name, phone number, address Email etc.
How we use your personal information:
- Collected by us personal information allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notifications and messages.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, competition, or similar promotional event, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, court order, in court proceedings, and / or on the basis of public requests or requests from government agencies on the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other socially important reasons.
- In the event of a reorganization, merger or sale, we may transfer the personal information we collect to the appropriate third party - the legal successor.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and abuse, as well as from unauthorized access, disclosure, alteration and destruction.
Respect for your privacy at the company level
In order to make sure that your personal information is safe, we bring the rules of confidentiality and security to our employees, and strictly monitor the implementation of confidentiality measures.
To successfully use the operation of extracting a root in practice, you need to become familiar with the properties of this operation.
All properties are formulated and proved only for non-negative values of the variables contained under the signs of the roots.
Theorem 1. Root nth degree (n = 2, 3, 4, ...) from the product of two non-negative chipcell is equal to the product roots of the nth powers of these numbers:
Comment:
1.
Theorem 1 remains valid for the case when the radical expression is the product of more than two non-negative numbers.
Theorem 2.If a,
and n is a natural number greater than 1, then the equality
Brief(albeit imprecise) formulation, which is more convenient to use in practice: the root of the fraction is equal to the fraction of the roots.
Theorem 1 allows us to multiply m only roots of the same degree
, i.e. only roots with the same index.
Theorem 3 If ,k is a natural number and n is a natural number greater than 1, then the equality
In other words, to raise a root to a natural degree, it is enough to raise a radical expression to this degree.
This is a consequence of Theorem 1. Indeed, for example, for k = 3, we obtain: In the same way, one can reason for any other natural value of the exponent k.
Theorem 4 If ,k, n are natural numbers greater than 1, then the equality
In other words, to extract a root from a root, it is enough to multiply the indices of the roots.
For example,
Be careful! We learned that four operations can be performed on roots: multiplication, division, exponentiation, and root extraction (from the root). But what about the addition and subtraction of roots? No way.
For example, instead of it is impossible to write Indeed, But it is obvious that
Theorem 5 If the indices of the root and the radical expression are multiplied or divided by the same natural number, then the value of the root will not change, i.e.
Examples of solving tasks
Example 1. Calculate
Decision. Using the first property of roots (Theorem 1), we get:
Example 2. Calculate
Decision. Convert the mixed number to an improper fraction.
We have Using the second property of the roots ( Theorem 2
), we get:
![]()
Example 3. Calculate: ![]()
Decision. Any formula in algebra, as you well know, is used not only "from left to right", but also "from right to left". So, the first property of roots means that it can be represented in the form and, conversely, can be replaced by an expression. The same applies to the second property of roots. With this in mind, let's perform the calculations.
Lesson and presentation on the topic: "Properties of the n-th root. Theorems"
Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an antivirus program.
Teaching aids and simulators in the online store "Integral" for grade 11
Interactive tutorial for grades 9-11 "Trigonometry"
Interactive tutorial for grades 10-11 "Logarithms"
Properties of the n-th root. Theorems
Guys, we continue to study the n-th roots of the real number. Like almost all mathematical objects, roots of the n-th degree have some properties, today we will study them.All the properties that we will consider are formulated and proved only for non-negative values of the variables contained under the root sign.
In the case of an odd root exponent, they are also performed for negative variables.
Theorem 1. The nth root of the product of two nonnegative numbers is equal to the product of the nth roots of these numbers: $ \ sqrt [n] (a * b) = \ sqrt [n] (a) * \ sqrt [n] ( b) $.
Let's prove the theorem.
Evidence. Guys, to prove the theorem, let's introduce new variables, denote:
$ \ sqrt [n] (a * b) = x $.
$ \ sqrt [n] (a) = y $.
$ \ sqrt [n] (b) = z $.
We need to prove that $ x = y * z $.
Note that the following identities hold:
$ a * b = x ^ n $.
$ a = y ^ n $.
$ b = z ^ n $.
Then the following identity holds: $ x ^ n = y ^ n * z ^ n = (y * z) ^ n $.
The powers of two non-negative numbers and their exponents are equal, then the bases of the powers themselves are equal. Hence $ x = y * z $, which is what was required to prove.
Theorem 2. If $ a≥0 $, $ b> 0 $ and n is a natural number greater than 1, then the following equality holds: $ \ sqrt [n] (\ frac (a) (b)) = \ frac (\ sqrt [ n] (a)) (\ sqrt [n] (b)) $.
That is, the root of the n-th degree of the quotient is equal to the quotient of the roots of the n-th degree.
Evidence.
For the proof, we will use a simplified table-like scheme:
Examples of calculating the root of the n-th power
Example.Calculate: $ \ sqrt (16 * 81 * 256) $.
Decision. Let's use Theorem 1: $ \ sqrt (16 * 81 * 256) = \ sqrt (16) * \ sqrt (81) * \ sqrt (256) = 2 * 3 * 4 = 24 $.
Example.
Calculate: $ \ sqrt (7 \ frac (19) (32)) $.
Decision. We represent the radical expression in the form wrong fraction: $ 7 \ frac (19) (32) = \ frac (7 * 32 + 19) (32) = \ frac (243) (32) $.
Let's use Theorem 2: $ \ sqrt (\ frac (243) (32)) = \ frac (\ sqrt (243)) (\ sqrt (32)) = \ frac (3) (2) = 1 \ frac (1) (2) $.
Example.
Calculate:
a) $ \ sqrt (24) * \ sqrt (54) $.
b) $ \ frac (\ sqrt (256)) (\ sqrt (4)) $.
Decision:
a) $ \ sqrt (24) * \ sqrt (54) = \ sqrt (24 * 54) = \ sqrt (8 * 3 * 2 * 27) = \ sqrt (16 * 81) = \ sqrt (16) * \ sqrt (81) = 2 * 3 = $ 6.
b) $ \ frac (\ sqrt (256)) (\ sqrt (4)) = \ sqrt (\ frac (256) (4)) = \ sqrt (64) = 24 $.
Theorem 3. If $ a≥0 $, k and n are natural numbers greater than 1, then the equality is true: $ (\ sqrt [n] (a)) ^ k = \ sqrt [n] (a ^ k) $.
To raise a root to a natural degree, it is enough to raise a radical expression to this degree.
Evidence.
let's consider special case for $ k = 3 $. We will use Theorem 1.
$ (\ sqrt [n] (a)) ^ k = \ sqrt [n] (a) * \ sqrt [n] (a) * \ sqrt [n] (a) = \ sqrt [n] (a * a * a) = \ sqrt [n] (a ^ 3) $.
The same can be proved for any other case. Guys, prove it yourself for the case when $ k = 4 $ and $ k = 6 $.
Theorem 4. If $ a≥0 $ b n, k are natural numbers greater than 1, then the equality is true: $ \ sqrt [n] (\ sqrt [k] (a)) = \ sqrt (a) $.
To extract a root from a root, it is enough to multiply the indices of the roots.
Evidence.
Let us prove again briefly using the table. For the proof, we use a simplified table-like scheme: 
Example.
$ \ sqrt (\ sqrt (a)) = \ sqrt (a) $.
$ \ sqrt (\ sqrt (a)) = \ sqrt (a) $.
$ \ sqrt (\ sqrt (a)) = \ sqrt (a) $.
Theorem 5. If the exponents of the root and the radical expression are multiplied by the same natural number, then the value of the root will not change: $ \ sqrt (a ^ (kp)) = \ sqrt [n] (a) $.
Evidence.
The principle of the proof of our theorem is the same as in other examples. Let's introduce new variables:
$ \ sqrt (a ^ (k * p)) = x => a ^ (k * p) = x ^ (n * p) $ (by definition).
$ \ sqrt [n] (a ^ k) = y => y ^ n = a ^ k $ (by definition).
We raise the last equality to the power p
$ (y ^ n) ^ p = y ^ (n * p) = (a ^ k) ^ p = a ^ (k * p) $.
Received:
$ y ^ (n * p) = a ^ (k * p) = x ^ (n * p) => x = y $.
That is, $ \ sqrt (a ^ (k * p)) = \ sqrt [n] (a ^ k) $, as required.
Examples:
$ \ sqrt (a ^ 5) = \ sqrt (a) $ (divided by 5).
$ \ sqrt (a ^ (22)) = \ sqrt (a ^ (11)) $ (divided by 2).
$ \ sqrt (a ^ 4) = \ sqrt (a ^ (12)) $ (multiplied by 3).
Example.
Perform actions: $ \ sqrt (a) * \ sqrt (a) $.
Decision.
The exponents of the roots are different numbers, so we cannot use Theorem 1, but applying Theorem 5, we can get equal exponents.
$ \ sqrt (a) = \ sqrt (a ^ 3) $ (multiplied by 3).
$ \ sqrt (a) = \ sqrt (a ^ 4) $ (multiplied by 4).
$ \ sqrt (a) * \ sqrt (a) = \ sqrt (a ^ 3) * \ sqrt (a ^ 4) = \ sqrt (a ^ 3 * a ^ 4) = \ sqrt (a ^ 7) $.
Tasks for independent solution
1. Calculate: $ \ sqrt (32 * 243 * 1024) $.2. Calculate: $ \ sqrt (7 \ frac (58) (81)) $.
3. Calculate:
a) $ \ sqrt (81) * \ sqrt (72) $.
b) $ \ frac (\ sqrt (1215)) (\ sqrt (5)) $.
4. Simplify:
a) $ \ sqrt (\ sqrt (a)) $.
b) $ \ sqrt (\ sqrt (a)) $.
c) $ \ sqrt (\ sqrt (a)) $.
5. Perform actions: $ \ sqrt (a ^ 2) * \ sqrt (a ^ 4) $.