1. Systems linear equations with parameter
Systems of linear equations with a parameter are solved by the same basic methods as ordinary systems of equations: the substitution method, the method of adding equations, and the graphical method. Knowledge of graphic interpretation linear systems makes it easy to answer the question about the number of roots and their existence.
Example 1.
Find all values for parameter a for which the system of equations has no solutions.
(x + (a 2 – 3)y = a,
(x + y = 2.
Solution.
Let's look at several ways to solve this task.
1 way. We use the property: the system has no solutions if the ratio of the coefficients in front of x is equal to the ratio of the coefficients in front of y, but not equal to the ratio free members(a/a 1 = b/b 1 ≠ c/c 1). Then we have:
1/1 = (a 2 – 3)/1 ≠ a/2 or system
(and 2 – 3 = 1,
(a ≠ 2.
From the first equation a 2 = 4, therefore, taking into account the condition that a ≠ 2, we get the answer.
Answer: a = -2.
Method 2. We solve by substitution method.
(2 – y + (a 2 – 3)y = a,
(x = 2 – y,
((a 2 – 3)y – y = a – 2,
(x = 2 – y.
After taking the common factor y out of brackets in the first equation, we get:
((a 2 – 4)y = a – 2,
(x = 2 – y.
The system has no solutions if the first equation has no solutions, that is
(and 2 – 4 = 0,
(a – 2 ≠ 0.
Obviously, a = ±2, but taking into account the second condition, the answer only comes with a minus answer.
Answer: a = -2.
Example 2.
Find all values for the parameter a for which the system of equations has an infinite number of solutions.
(8x + ay = 2,
(ax + 2y = 1.
Solution.
According to the property, if the ratio of the coefficients of x and y is the same, and is equal to the ratio of the free members of the system, then it has an infinite number of solutions (i.e. a/a 1 = b/b 1 = c/c 1). Therefore 8/a = a/2 = 2/1. Solving each of the resulting equations, we find that a = 4 is the answer in this example.
Answer: a = 4.
2. Systems rational equations with parameter
Example 3.
(3|x| + y = 2,
(|x| + 2y = a.
Solution.
Let's multiply the first equation of the system by 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Subtracting the second equation from the first, we get 5|x| = 4 – a. This equation will have the only solution for a = 4. In other cases, this equation will have two solutions (for a< 4) или ни одного (при а > 4).
Answer: a = 4.
Example 4.
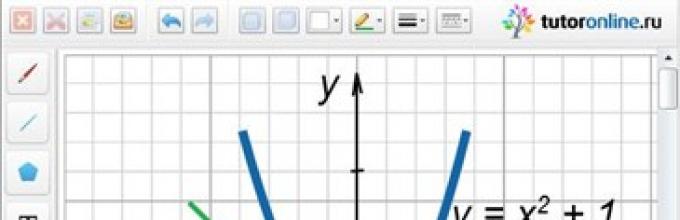
Find all values of the parameter a for which the system of equations has a unique solution.
(x + y = a,
(y – x 2 = 1.
Solution.
We will solve this system using the graphical method. Thus, the graph of the second equation of the system is a parabola raised along the Oy axis upward by one unit segment. The first equation specifies a set of lines parallel to the line y = -x (Figure 1). It is clearly seen from the figure that the system has a solution if the straight line y = -x + a is tangent to the parabola at a point with coordinates (-0.5, 1.25). Substituting these coordinates into the straight line equation instead of x and y, we find the value of parameter a: 
1.25 = 0.5 + a;
Answer: a = 0.75.
Example 5.
Using the substitution method, find out at what value of the parameter a, the system has a unique solution.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Solution.
From the first equation we express y and substitute it into the second:
(y = ax – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.
Let us reduce the second equation to the form kx = b, which will have a unique solution for k ≠ 0. We have:
ax + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
a 2 x + 3ax = 2 + a 2 + 3a + 2.
We represent the square trinomial a 2 + 3a + 2 as a product of brackets
(a + 2)(a + 1), and on the left we take x out of brackets:
(a 2 + 3a)x = 2 + (a + 2)(a + 1).
Obviously, a 2 + 3a should not be equal to zero, therefore,
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, which means a ≠ 0 and ≠ -3.
Answer: a ≠ 0; ≠ -3.
Example 6.
Using the graphical solution method, determine at what value of parameter a the system has a unique solution.
(x 2 + y 2 = 9,
(y – |x| = a.
Solution.
Based on the condition, we construct a circle with a center at the origin and a radius of 3 unit segments; this is what is specified by the first equation of the system
x 2 + y 2 = 9. The second equation of the system (y = |x| + a) is a broken line. By using figure 2 We consider all possible cases of its location relative to the circle. It is easy to see that a = 3. 
Answer: a = 3.
Still have questions? Don't know how to solve systems of equations?
To get help from a tutor, register.
The first lesson is free!
website, when copying material in full or in part, a link to the source is required.
For what values of the parameter $a$ does the inequality $()-x^2 + (a + 2)x - 8a - 1 > 0$ have at least one solution?
Solution
Let us reduce this inequality to a positive coefficient for $x^2$:
$()-x^2 + (a + 2)x - 8a - 1 > 0 \quad \Leftrightarrow \quad x^2 - (a + 2)x + 8a + 1< 0 .$
Let's calculate the discriminant: $D = (a + 2)^2 - 4(8a + 1) = a^2 + 4a + 4 - 32a - 4 = a^2 - 28a$. For this inequality to have a solution, it is necessary that at least one point of the parabola lies below the $x$ axis. Since the branches of the parabola are directed upward, this requires that the square trinomial on the left side of the inequality have two roots, that is, its discriminant be positive. We come to the need to decide quadratic inequality$a^2 - 28a > 0$. The square trinomial $a^2 - 28a$ has two roots: $a_1 = 0$, $a_2 = 28$. Therefore, the inequality $a^2 - 28a > 0$ is satisfied by the intervals $a \in (-\infty; 0) \cup (28; + \infty)$.
Answer.$a \in (-\infty; 0) \cup (28; + \infty)$.
For what values of the parameter $a$ does the equation $(a-2)x^2-2ax+a+3=0$ have at least one root, and all roots are positive?
Solution
Let $a=2$. Then the equation takes the form $() - 4x +5 = 0$, from which we obtain that $x=\dfrac(5)(4)$ is a positive root.
Let now $a\ne 2$. This results in a quadratic equation. Let us first determine at what values of the parameter $a$ this equation has roots. Its discriminant must be non-negative. That is:
$ D = 4a^2 - 4(a-2)(a+3) =() -4a+24\geqslant 0\Leftrightarrow a\leqslant 6.$
The roots by condition must be positive, therefore, from Vieta’s theorem we obtain the system:
$ \begin(cases)x_1 + x_2 = \dfrac(2a)(a - 2)>0,\\ x_1x_2 = \dfrac(a + 3)(a - 2)> 0,\\a\leqslant 6\end (cases) \quad \Leftrightarrow \quad \begin(cases)a\in(- \infty;0)\cup(2; +\infty), \\ a\in(- \infty;-3)\cup( 2; +\infty), \\ a\in(-\infty;6] \end(cases)\quad\Leftrightarrow \quad a\in(-\infty;-3)\cup(2;6]. $
We combine the answers and get the required set: $a\in(-\infty;-3)\cup$.
Answer.$a\in(-\infty;-3)\cup$.
For what values of the parameter $a$ does the inequality $ax^2 + 4ax + 5 \leqslant 0$ have no solutions?
Solution
- If $a = 0$, then this inequality degenerates into the inequality $5 \leqslant 0$, which has no solutions. Therefore, the value $a = 0$ satisfies the conditions of the problem.
- If $a > 0$, then the graph quadratic trinomial on the left side of the inequality there is a parabola with branches directed upward. Let's calculate $\dfrac(D)(4) = 4a^2 - 5a$. The inequality has no solutions if the parabola is located above the x-axis, that is, when the square trinomial has no roots ($D< 0$). Решим неравенство $4a^2 - 5a < 0$. Корнями квадратного трёхчлена $4a^2 - 5a$ являются числа $a_1 = 0$ и $a_2 = \dfrac{5}{4}$, поэтому $D < 0$ при $0 < a < \dfrac{5}{4}$. Значит, из positive values$a$ suitable numbers $a \in \left(0; \dfrac(5)(4)\right)$.
- If $a< 0$, то график квадратного трехчлена в левой части неравенства - парабола с ветвями, направленными вниз. Значит, обязательно найдутся значения $х$, для которых трёхчлен отрицателен. Следовательно, все значения $a < 0$ не подходят.
Answer.$a \in \left$ lies between the roots, so there must be two roots (meaning $a\ne 0$). If the branches of the parabola $y = ax^2 + (a + 3)x - 3a$ are directed upward, then $y(-1)< 0$ и $y(1) < 0$; если же они направлены вниз, то $y(-1) >0$ and $y(1) > 0$.
Case I. Let $a > 0$. Then
$\left\( \begin(array)(l) y(-1)=a-(a+3)-3a=-3a-3<0 \\ y(1)=a+(a+3)-3a=-a+3<0 \\ a>0 \end(array) \right. \quad \Leftrightarrow \quad \left\( \begin(array)(l) a>-1 \\ a>3 \\ a>0 \end(array) \right.\quad \Leftrightarrow \quad a>3. $
That is, in this case it turns out that all $a > 3$ are suitable.
Case II. Let $a< 0$. Тогда
$\left\( \begin(array)(l) y(-1)=a-(a+3)-3a=-3a-3>0 \\ y(1)=a+(a+3)-3a =-a+3>0 \\ a<0 \end{array} \right.\quad \Leftrightarrow \quad \left\{ \begin{array}{l} a<-1 \\ a<3 \\ a<0 \end{array} \right.\quad \Leftrightarrow \quad a<-1.$
That is, in this case it turns out that all $a are suitable< -1$.
Answer.$a\in (-\infty ;-1)\cup (3;+\infty)$
Find all values of the parameter $a$, for each of which the system of equations
$ \begin(cases) x^2+y^2 = 2a, \\ 2xy=2a-1 \end(cases) $
has exactly two solutions.
Solution
Subtract the second from the first: $(x-y)^2 = 1$. Then
$ \left[\begin(array)(l) x-y = 1, \\ x-y = -1 \end(array)\right. \quad \Leftrightarrow \quad \left[\begin(array)(l) x = y+1, \\ x = y-1. \end(array)\right. $
Substituting the resulting expressions into the second equation of the system, we obtain two quadratic equations: $2y^2 + 2y - 2a + 1 = 0$ and $2y^2 - 2y - 2a + 1 =0$. The discriminant of each of them is $D = 16a-4$.
Note that it cannot happen that a pair of roots of the first of quadratic equations coincides with a pair of roots of the second quadratic equation, since the sum of the roots of the first is $-1$, and the second is 1.
This means that each of these equations must have one root, then the original system will have two solutions. That is, $D = 16a - 4 = 0$.
Answer.$a=\dfrac(1)(4)$
Find all values of the parameter $a$ for each of which the equation $4x-|3x-|x+a||=9|x-3|$ has two roots.
Solution
Let's rewrite the equation as:
$ 9|x-3|-4x+|3x-|x+a|| = 0.$
Consider the function $f(x) = 9|x-3|-4x+|3x-|x+a||$.
When $x\geqslant 3$ the first module is expanded with a plus sign, and the function takes the form: $f(x) = 5x-27+|3x-|x+a||$. It is obvious that with any expansion of modules the result will be linear function with the coefficient $k\geqslant 5-3-1=1>0$, that is, this function increases indefinitely over a given interval.
Let us now consider the interval $x<3$. В этом случае первый модуль раскрывается с минусом, и функция принимает следующий вид: $f(x) = - 13x+27+|3x-|x+a||$. При любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом $k\leqslant - 13+3+1 = - 9<0$, то есть на этом промежутке функция убывает.
So, we got that $x=3$ is the minimum point of this function. This means that in order for the original equation to have two solutions, the value of the function at the minimum point must be less than zero. That is, the following inequality holds: $f(3)<0$.
$ 12-|9-|3+a||>0 \quad \Leftrightarrow \quad |9-|3+a||< 12 \quad \Leftrightarrow \quad -12 < 9-|3+a| < 12 \quad \Leftrightarrow \quad$
$\Leftrightarrow\quad |3+a|< 21 \quad \Leftrightarrow \quad - 21 < 3+a < 21 \quad \Leftrightarrow \quad -24 Answer.$a \in (-24; 18)$ For what values of the parameter $a$ does the equation $5^(2x)-3\cdot 5^x+a-1=0$ have a unique root? Let's make a replacement: $t = 5^x > 0$. Then the original equation takes the form of a quadratic equation: $t^2-3t+a-1 =0$. The original equation will have a single root if this equation has one positive root or two roots, one of which is positive and the other negative. The discriminant of the equation is: $D = 13-4a$. This equation will have one root if the resulting discriminant turns out to be equal to zero, that is, for $a = \dfrac(13)(4)$. In this case, the root $t=\dfrac(3)(2) > 0$, so this value of $a$ is suitable. If there are two roots, one of which is positive, the other is non-positive, then $D = 13-4a > 0$, $x_1+x_2 = 3 > 0$ and $x_1x_2 = a - 1 \leqslant 0$. That is, $a\in(-\infty;1]$ Answer.$a\in(-\infty;1]\cup\left\(\dfrac(13)(4)\right\)$ Find all values of the parameter $a$ for which the system $ \begin(cases)\log_a y = (x^2-2x)^2, \\ x^2+y=2x\end(cases) $ has exactly two solutions. Let's transform the system to the following form: $ \begin(cases) \log_a y = (2x-x^2)^2, \\ y = 2x-x^2. \end(cases)$ Since the parameter $a$ is at the base of the logarithm, the following restrictions are imposed on it: $a>0$, $a \ne 1$. Since the variable $y$ is the argument of the logarithm, then $y > 0$. Having combined both equations of the system, we move on to the equation: $\log_a y = y^2$. Depending on what values the parameter $a$ takes, two cases are possible: Answer.$a\in(0;1)$ Let's consider the case when $a > 1$. Since for large absolute values of $t$ the graph of the function $f(t) = a^t$ lies above the straight line $g(t) = t$, then the only common point can only be a point of tangency. Let $t_0$ be the point of tangency. At this point, the derivative of $f(t) = a^t$ equals unity (tangent of the tangent angle), in addition, the values of both functions coincide, that is, the system takes place: $ \begin(cases) a^(t_0)\ln a = 1, \\ a^(t_0) = t_0 \end(cases) \quad \Leftrightarrow \quad \begin(cases) a^(t_0) = \dfrac (1)(\ln a), \\ a^(\tau) = \tau \end(cases) $ Whence $t_0 = \dfrac(1)(\ln a)$. $ a^(\frac(1)(\ln a))\ln a = 1 \quad \Leftrightarrow \quad a^(\log_a e) =\frac(1)(\ln a) \quad \Leftrightarrow \quad a = e^(\frac(1)(e)). $ At the same time, others common points at the straight line and exponential function obviously not. Answer.$a \in (0;1] \cup \left\(e^(e^(-1))\right\)$ The use of equations is widespread in our lives. They are used in many calculations, construction of structures and even sports. Man used equations in ancient times, and since then their use has only increased. In mathematics, there are problems in which it is necessary to search for solutions to linear and quadratic equations in general view or search for the number of roots that the equation has depending on the value of the parameter. All these tasks have parameters. Consider the following equations as an illustrative example: \[y = kx,\] where \ are variables, \ is a parameter; \[y = kx + b,\] where \ are variables, \ is a parameter; \[аx^2 + bх + с = 0,\] where \ is a variable, \[а, b, с\] is a parameter. Solving an equation with a parameter means, as a rule, solving an infinite set of equations. However, following a certain algorithm, you can easily solve the following equations: 1. Determine the “control” values of the parameter. 2. Solve the original equation for [\x\] with the parameter values defined in the first paragraph. 3. Solve the original equation for [\x\] for parameter values different from those chosen in the first paragraph. Let's say we're given the following equation: \[\mid 6 - x \mid = a.\] Having analyzed the initial data, it is clear that a \[\ge 0.\] According to the modulus rule, we express \ Answer: \where\ You can solve the equation on our website https://site. The free online solver will allow you to solve online equations of any complexity in a matter of seconds. All you need to do is simply enter your data into the solver. You can also watch video instructions and learn how to solve the equation on our website. And if you still have questions, you can ask them in our VKontakte group http://vk.com/pocketteacher. Join our group, we are always happy to help you.Solution
Solution
Where can I solve an equation with a parameter online?