Functiony = sinx
The graph of the function is a sinusoid.
The complete non-repeating portion of a sine wave is called a sine wave.
Half a sine wave is called a half sine wave (or arc).
Function propertiesy =
sinx:
3) This is an odd function. 4) This continuous function.
6) On the segment [-π/2; π/2] function increases on the interval [π/2; 3π/2] – decreases. 7) On intervals the function takes positive values. 8) Intervals of increasing function: [-π/2 + 2πn; π/2 + 2πn]. 9) Minimum points of the function: -π/2 + 2πn. |
To graph a function y= sin x It is convenient to use the following scales:
On a sheet of paper with a square, we take the length of two squares as a unit of segment.
On axis x Let's measure the length π. At the same time, for convenience, we present 3.14 in the form of 3 - that is, without a fraction. Then on a sheet of paper in a cell π will be 6 cells (three times 2 cells). And each cell will receive its own natural name (from the first to the sixth): π/6, π/3, π/2, 2π/3, 5π/6, π. These are the meanings x.
On the y-axis we mark 1, which includes two cells.
Let's create a table of function values using our values x:
√3 | √3 |
Next, let's create a schedule. It will turn out to be a half wave, highest point which (π/2; 1). This is the graph of the function y= sin x on the segment. Let's add a symmetrical half-wave to the constructed graph (symmetrical relative to the origin, that is, on the segment -π). The crest of this half-wave is under the x-axis with coordinates (-1; -1). The result will be a wave. This is the graph of the function y= sin x on the segment [-π; π].
You can continue the wave by constructing it on the segment [π; 3π], [π; 5π], [π; 7π], etc. On all these segments, the graph of the function will look the same as on the segment [-π; π]. You will get a continuous wavy line with identical waves.
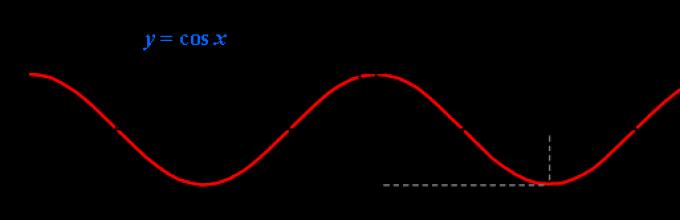
Functiony = cosx.
The graph of a function is a sine wave (sometimes called a cosine wave).

Function propertiesy = cosx:
1) The domain of definition of a function is the set of real numbers. 2) The range of function values is the segment [–1; 1] 3) This is an even function. 4) This is a continuous function. 5) Coordinates of the intersection points of the graph: 6) On the segment the function decreases, on the segment [π; 2π] – increases. 7) On intervals [-π/2 + 2πn; π/2 + 2πn] function takes positive values. 8) Increasing intervals: [-π + 2πn; 2πn]. 9) Minimum points of the function: π + 2πn. 10) The function is limited from above and below. Lowest value functions –1, 11) This periodic function with period 2π (T = 2π) |
Functiony = mf(x).
Let's take the previous function y=cos x. As you already know, its graph is a sine wave. If we multiply the cosine of this function by a certain number m, then the wave will expand from the axis x(or will shrink, depending on the value of m).
This new wave will be the graph of the function y = mf(x), where m is any real number.
Thus, the function y = mf(x) is the familiar function y = f(x) multiplied by m.
Ifm< 1, то синусоида сжимается к оси x by the coefficientm. Ifm > 1, then the sinusoid is stretched from the axisx by the coefficientm.
When performing stretching or compression, you can first plot only one half-wave of a sine wave, and then complete the entire graph.
Functiony = f(kx).
If the function y =mf(x) leads to stretching of the sinusoid from the axis x or compression towards the axis x, then the function y = f(kx) leads to stretching from the axis y or compression towards the axis y.
Moreover, k is any real number.
At 0< k< 1 синусоида растягивается от оси y by the coefficientk. Ifk > 1, then the sinusoid is compressed towards the axisy by the coefficientk.
When graphing this function, you can first build one half-wave of a sine wave, and then use it to complete the entire graph.
Functiony = tgx.
Function graph y= tg x is a tangent.
It is enough to construct part of the graph in the interval from 0 to π/2, and then you can symmetrically continue it in the interval from 0 to 3π/2.

Function propertiesy = tgx:
Functiony = ctgx
Function graph y=ctg x is also a tangentoid (it is sometimes called a cotangentoid).

Function propertiesy = ctgx:
How to graph the function y=sin x? First, let's look at the sine graph on the interval.
We take a single segment 2 cells long in the notebook. On the Oy axis we mark one.
For convenience, we round the number π/2 to 1.5 (and not to 1.6, as required by the rounding rules). In this case, a segment of length π/2 corresponds to 3 cells.
On the Ox axis we mark not single segments, but segments of length π/2 (every 3 cells). Accordingly, a segment of length π corresponds to 6 cells, and a segment of length π/6 corresponds to 1 cell.
With this choice of a unit segment, the graph depicted on a sheet of notebook in a box corresponds as much as possible to the graph of the function y=sin x.
Let's make a table of sine values on the interval:
We mark the resulting points on the coordinate plane:

Since y=sin x is an odd function, the sine graph is symmetrical with respect to the origin - point O(0;0). Taking this fact into account, let’s continue plotting the graph to the left, then the points -π:

The function y=sin x is periodic with period T=2π. Therefore, the graph of a function taken on the interval [-π;π] is repeated an infinite number of times to the right and to the left.










 Back Forward
Back Forward
Attention! Slide previews are for informational purposes only and may not represent all the features of the presentation. If you are interested in this work, please download the full version.
Iron rusts without finding any use,
Still water rots or freezes in the cold,
and a person’s mind, not finding any use for itself, languishes.
Leonardo da Vinci
Technologies used: problem-based learning, critical thinking, communicative communication.
Goals:
- Development of cognitive interest in learning.
- Studying the properties of the function y = sin x.
- Formation of practical skills in constructing a graph of the function y = sin x based on the studied theoretical material.
Tasks:
1. Use the existing potential of knowledge about the properties of the function y = sin x in specific situations.
2. Apply conscious establishment of connections between analytical and geometric models of the function y = sin x.
Develop initiative, a certain willingness and interest in finding a solution; the ability to make decisions, not stop there, and defend your point of view.
To foster in students cognitive activity, a sense of responsibility, respect for each other, mutual understanding, mutual support, and self-confidence; culture of communication.
Lesson progress
Stage 1. Updating basic knowledge, motivating learning new material
"Entering the lesson."
There are 3 statements written on the board:
- Trigonometric sin equation t = a always has solutions.
- The graph of an odd function can be constructed using a symmetry transformation about the Oy axis.
- A trigonometric function can be graphed using one principal half-wave.
Students discuss in pairs: are the statements true? (1 minute). The results of the initial discussion (yes, no) are then entered into the table in the "Before" column.
The teacher sets the goals and objectives of the lesson.
2. Updating knowledge (frontally on a model of a trigonometric circle).
We have already become acquainted with the function s = sin t.
1) What values can the variable t take. What is the scope of this function?
2) In what interval are the values of the expression sin t contained? Find the largest and smallest values of the function s = sin t.
3) Solve the equation sin t = 0.
4) What happens to the ordinate of a point as it moves along the first quarter? (the ordinate increases). What happens to the ordinate of a point as it moves along the second quarter? (the ordinate gradually decreases). How does this relate to the monotonicity of the function? (the function s = sin t increases on the segment and decreases on the segment ).
5) Let's write the function s = sin t in the form y = sin x that is familiar to us (we will construct it in the usual xOy coordinate system) and compile a table of the values of this function.
| X | 0 | ||||||
| at | 0 | 1 | 0 |
Stage 2. Perception, comprehension, primary consolidation, involuntary memorization
Stage 4. Primary systematization of knowledge and methods of activity, their transfer and application in new situations
6. No. 10.18 (b,c)
Stage 5. Final control, correction, assessment and self-assessment
7. Return to the statements (beginning of the lesson), discuss using the properties of the trigonometric function y = sin x, and fill in the “After” column in the table.
8. D/z: clause 10, No. 10.7(a), 10.8(b), 10.11(b), 10.16(a)
Centered at a point A.
α
- angle expressed in radians.
Definition
Sine (sin α)- This trigonometric function, depending on the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio length of the opposite side |BC| to the length of the hypotenuse |AC|.
Cosine (cos α) is a trigonometric function depending on the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio of the length of the adjacent leg |AB| to the length of the hypotenuse |AC|.
Accepted notations
;
;
.
;
;
.
Graph of the sine function, y = sin x
Graph of the cosine function, y = cos x

Properties of sine and cosine
Periodicity
Functions y = sin x and y = cos x periodic with period 2π.
Parity
The sine function is odd. The cosine function is even.
Domain of definition and values, extrema, increase, decrease
The sine and cosine functions are continuous in their domain of definition, that is, for all x (see proof of continuity). Their main properties are presented in the table (n - integer).
| y = sin x | y = cos x | |
| Scope and continuity | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| Range of values | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Increasing | ||
| Descending | ||
| Maxima, y = 1 | ||
| Minima, y = - 1 | ||
| Zeros, y = 0 | ||
| Intercept points with the ordinate axis, x = 0 | y = 0 | y = 1 |
Basic formulas
Sum of squares of sine and cosine
Formulas for sine and cosine from sum and difference
;
;
Formulas for the product of sines and cosines
Sum and difference formulas
Expressing sine through cosine
;
;
;
.
Expressing cosine through sine
;
;
;
.
Expression through tangent
; .
When , we have:
;
.
At :
;
.
Table of sines and cosines, tangents and cotangents
This table shows the values of sines and cosines for certain values of the argument. 
Expressions through complex variables
;
Euler's formula
Expressions through hyperbolic functions
;
;
Derivatives
; . Deriving formulas > > >
Derivatives of nth order:
{ -∞ <
x < +∞ }
Secant, cosecant
Inverse functions
Inverse functions to sine and cosine are arcsine and arccosine, respectively.
Arcsine, arcsin
Arccosine, arccos
Used literature:
I.N. Bronstein, K.A. Semendyaev, Handbook of mathematics for engineers and college students, “Lan”, 2009.
Geometric definition of sine and cosine
\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)
α - angle expressed in radians.
Sine (sin α) is a trigonometric function of the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio of the length of the opposite leg |BC| to the length of the hypotenuse |AB|.
Cosine (cos α) is a trigonometric function of the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio of the length of the adjacent leg |AC| to the length of the hypotenuse |AB|.
Trigonometric definition
Using the formulas above, you can find the sine and cosine of an acute angle. But you need to learn how to calculate the sine and cosine of an angle of arbitrary size. A right triangle does not provide this opportunity ( obtuse angle, for example, cannot be in it); therefore, more is needed general definition sine and cosine, containing these formulas as a special case.
Comes to the rescue trigonometric circle. Let some angle be given; it corresponds to the point of the same name on the trigonometric circle.
Rice. 2. Trigonometric definition of sine and cosine
The cosine of an angle is the abscissa of a point. The sine of an angle is the ordinate of a point.
In Fig. 2 the angle is taken acute, and it is easy to understand that this definition coincides with the general geometric definition. In fact, we see right triangle with a unit hypotenuse O and an acute angle. The adjacent leg of this triangle is cos (compare with Fig. 1) and at the same time the abscissa of the point; the opposite side is sin (as in Fig. 1) and at the same time the ordinate of the point.
But now we are no longer constrained by the first quarter and have the opportunity to extend this definition to any angle. In Fig. Figure 3 shows what the sine and cosine of an angle are in the second, third and fourth quarters.

Rice. 3. Sine and cosine in II, III and IV quarters
Table values of sine and cosine
Zero angle \(\LARGE 0^(\circ ) \)
The abscissa of point 0 is equal to 1, the ordinate of point 0 is equal to 0. Hence,
cos 0 = 1 sin 0 = 0

Fig 4. Zero angle
Angle \(\LARGE \frac(\pi)(6) = 30^(\circ )\)
We see a right triangle with a unit hypotenuse and an acute angle of 30°. As you know, the leg lying opposite the angle 30° is equal to half the hypotenuse 1; in other words, the vertical leg is equal to 1/2 and, therefore,
\[ \sin \frac(\pi)(6) =\frac(1)(2) \]
We find the horizontal leg using the Pythagorean theorem (or, which is the same, we find the cosine using the main trigonometric identity):
\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \right)^(2) ) =\frac(\sqrt(3) )(2 ) \]
1 Why does this happen? Cut equilateral triangle with side 2 along its height! It will split into two right triangles with a hypotenuse of 2, an acute angle of 30° and a shorter leg of 1.

Fig 5. Angle π/6
Angle \(\LARGE \frac(\pi)(4) = 45^(\circ )\)
In this case, the right triangle is isosceles; The sine and cosine of an angle of 45° are equal to each other. Let us denote them by x for now. We have:
\[ x^(2) + x^(2) = 1 \]
whence \(x=\frac(\sqrt(2) )(2) \). Hence,
\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Fig 5. Angle π/4
Properties of sine and cosine
Accepted notations
\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).
\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).
Periodicity
The functions y = sin x and y = cos x are periodic with a period of 2π.
\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)
Parity
The sine function is odd. The cosine function is even.
\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)
Areas of definition and values, extrema, increase, decrease
The basic properties of sine and cosine are presented in the table ( n- whole).
| \(\small< x < \) | \(\small -\pi + 2\pi n \) \(\small< x < \) \(\small 2\pi n \) | |
| Descending | \(\small \dfrac(\pi)2 + 2\pi n \)\(\small< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \) | \(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \) |
| Maxima, \(\small x = \) \(\small \dfrac(\pi)2 + 2\pi n \) | \(\small x = 2\pi n\) | |
| Minima, \(\small x = \) \(\small -\dfrac(\pi)2 + 2\pi n \) | \(\small x = \) \(\small \pi + 2\pi n \) | |
| Zeros, \(\small x = \pi n\) | \(\small x = \dfrac(\pi)2 + \pi n \) | |
| Y-axis intersection points, x = 0 | y = 0 | y = 1 |
Basic formulas containing sine and cosine
Sum of squares
\(\sin^2 x + \cos^2 x = 1\)
Sine and cosine formulas for sum and difference
\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)
\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \right) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \right) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)
Formulas for the product of sines and cosines
\(\sin x \cos y = \) \(\dfrac12 (\Large [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Large [) \cos(x - y) - \cos(x + y) (\Large ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Large [) \cos(x - y) + \cos(x + y) (\Large ]) \)
\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)
Sum and difference formulas
\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)
Expressing sine through cosine
\(\sin x = \cos\left(\dfrac(\pi)2 - x \right) = \)\(\cos\left(x - \dfrac(\pi)2 \right) = - \cos\left(x + \dfrac(\pi)2 \right) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).
Expressing cosine through sine
\(\cos x = \sin\left(\dfrac(\pi)2 - x \right) = \)\(- \sin\left(x - \dfrac(\pi)2 \right) = \sin\left(x + \dfrac(\pi)2 \right) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).
Expression through tangent
\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).
At \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).
At \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \)
:
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).
Table of sines and cosines, tangents and cotangents
This table shows the values of sines and cosines for certain values of the argument.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="Table of sines and cosines" title="Table of sines and cosines" ]!}
Expressions through complex variables
\(i^2 = -1\)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)
Euler's formula
\(e^(iz) = \cos z + i \sin z \)
Expressions through hyperbolic functions
\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)
Derivatives
\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Deriving formulas > > >
Derivatives of nth order:
\(\left(\sin x \right)^((n)) = \sin\left(x + n\dfrac(\pi)2 \right) \)\(\left(\cos x \right)^((n)) = \cos\left(x + n\dfrac(\pi)2 \right) \).
Integrals
\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
See also Table section indefinite integrals >>>
Series expansions
\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \)
!} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \)
!} \(\( - \infty< x < \infty \} \)
Secant, cosecant
\(\sec x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)
Inverse functions
The inverse functions of sine and cosine are arcsine and arccosine, respectively.
Arcsine, arcsin
\(y = \arcsin x\) \(\left\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \right\) \)
\(\sin(\arcsin x) = x\)
\(\arcsin(\sin x) = x\) \(\left\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \right\) \)
Arccosine, arccos
\(y = \arccos x\) \(\left\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x\) \(\( 0 \leqslant x \leqslant \pi \) \)
Used literature:
I.N. Bronstein, K.A. Semendyaev, Handbook of mathematics for engineers and college students, “Lan”, 2009.
To perform calculations, you must enable ActiveX controls!