1. The first two signs of equality of right triangles.
For two triangles to be equal, it is enough that three elements of one triangle are equal to the corresponding elements of the other triangle, and these elements must certainly include at least one side.
Since all right angles are equal to each other, right triangles already have one equal element, namely one right angle.

It follows that right triangles are congruent:
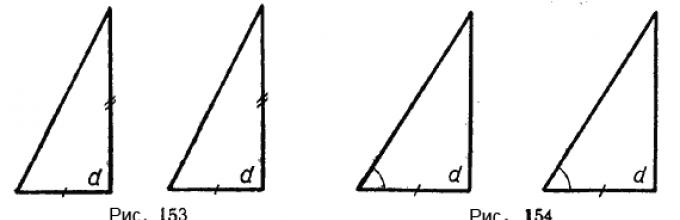
if the legs of one triangle are respectively equal to the legs of another triangle (Fig. 153);
if the leg and the adjacent acute angle of one triangle are respectively equal to the leg and the adjacent acute angle of the other triangle (Fig. 154).
Let us now prove two theorems that establish two more criteria for the equality of right triangles.
Theorems on tests for the equality of right triangles
Theorem 1. If the hypotenuse and acute angle of one triangle are respectively equal to the hypotenuse and acute angle of another triangle, then such right triangles are congruent.To prove this theorem, let us construct two rectangular angles ABC and A'B'C', in which the angles A and A' are equal, the hypotenuses AB and A'B' are also equal, and the angles C and C' are right (Fig. 157) .

Let’s superimpose triangle A’B’C’ onto triangle ABC so that vertex A’ coincides with vertex A, hypotenuse A’B’ coincides with equal hypotenuse AB. Then, due to the equality of angles A and A’, the side A’C’ will go along the side AC; leg B’C’ will coincide with leg BC: both of them are perpendiculars drawn to one straight line AC from one point B. This means that vertices C and C’ will coincide.
Triangle ABC coincides with triangle A'B'C'.
Therefore, \(\Delta\)ABC = \(\Delta\)A'B'C'.
This theorem gives the 3rd criterion for the equality of right triangles (by the hypotenuse and the acute angle).
Theorem 2. If the hypotenuse and leg of one triangle are respectively equal to the hypotenuse and leg of another triangle, then such right triangles are congruent.
To prove this, let's construct two rectangular triangle ABC and A'B'C', in which the angles C and C' are right, the legs AC and A'C' are equal, the hypotenuses AB and A'B' are also equal (Fig. 158).

Let's draw a straight line MN and mark point C on it, from this point we draw a perpendicular SC to straight line MN. Then we will superimpose the right angle of the triangle ABC onto the right angle KSM so that their vertices are aligned and the leg AC goes along the ray SC, then the leg BC goes along the ray CM. The right angle of the triangle A'B'C' will be superimposed on the right angle KCN so that their vertices are aligned and the leg A'C' goes along the ray SK, then the leg C'B' goes along the ray CN. The vertices A and A' will coincide due to the equality of the legs AC and A'C'.
Triangles ABC and A'B'C' will form together isosceles triangle BAB’, in which AC will be the height and bisector, and therefore the axis of symmetry of the triangle BAB’. It follows from this that \(\Delta\)ABC = \(\Delta\)A’B’C’.
This theorem gives the 4th criterion for the equality of right triangles (by hypotenuse and leg).
So, all the signs of equality of right triangles:
1. If two legs of one right triangle are respectively equal to two legs of another right triangle, then such right triangles are equal2. If the leg and the adjacent acute angle of one right triangle are respectively equal to the leg and the adjacent acute angle of another right triangle, then such right triangles are congruent
3. If the leg and the opposite acute angle of one right triangle are respectively equal to the leg and the opposite acute angle of another right triangle, then such right triangles are congruent
4. If the hypotenuse and acute angle of one right triangle are respectively equal to the hypotenuse and acute angle of another right triangle, then such right triangles are congruent
5. If the leg and hypotenuse of one right triangle are respectively equal to the leg and hypotenuse of another right triangle, then such right triangles are congruent
To establish the equality of right triangles, it is enough to know that two elements of one triangle are respectively equal to two elements of another triangle (excluding the right angle). This, of course, does not apply to the equality of two angles of one triangle to two angles of another triangle.
Since in right triangle the angle between two legs is a straight line, and any two right angles are equal, then from the first sign of equality of triangles it follows:
If the legs of one right triangle are correspondingly equal to the legs of another, then such triangles are congruent (Fig. 5).
If the leg and the adjacent acute angle of one right triangle are respectively equal to the leg and the adjacent angle of another triangle, then such triangles are congruent (Fig. 6).

Let's consider two more signs of equality of right triangles.

THEOREM . If the hypotenuse and acute angle of one right triangle are equal to the hypotenuse and acute angle of another triangle, then such triangles are congruent (Fig. 7).
PROOF. From property 1є § it follows that in such triangles the other two acute angles are also equal, therefore the triangles are equal according to the second sign of equality of triangles, that is, along the side (hypotenuse) and two adjacent angles.
Q.E.D.
THEOREM . If the hypotenuse and leg of one right triangle are respectively equal to the hypotenuse and leg of another triangle, then such triangles are congruent.
PROOF. Let's consider triangles ABC and A 1 B 1 C 1 , whose angles C and C 1 are right angles, AB = A 1 B 1 , BC = B 1 C 1 (Fig. 8).

Because< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с acute angle B 1 A 1 C 1). But this is impossible, so vertices A and A 1 will coincide. Therefore, triangles ABC A 1 B 1 C 1 will be completely compatible, that is, they are equal.
Q.E.D.
Pythagorean theorem
Its significance lies in the fact that most of the theorems of geometry can be deduced from it or with its help. One of the theorems makes it possible to verify that if a perpendicular and inclined lines are drawn to it from a point outside a line, then: a) the inclined lines are equal if their projections are equal; b) the one that is inclined is larger, which has a larger projection.
The Pythagorean theorem was the first statement that related the lengths of the sides of triangles. Then we learned how to find side lengths and angles of acute and obtuse triangles. The whole science of trigonometry arose (“trigon” means “triangle” in Greek). This science has found application in land surveying. But even earlier, with its help, they learned to measure imaginary triangles in the sky, the vertices of which were stars. Now trigonometry is even used to measure distances between spacecraft.
Using the properties of the areas of polygons, we will now establish a remarkable relationship between the hypotenuse and the legs of a right triangle. The theorem we will prove is called the Pythagorean theorem, which is the most important theorem in geometry.
If we are given a triangle,
And with a right angle at that,
That is the square of the hypotenuse
We can always easily find:
We square the legs,
We find the sum of powers
And in such a simple way
We will come to the result.
THEOREM. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.
PROOF. Consider a right triangle with legs a, b and c (Fig. 9 a).

Let us prove that c 2 = a 2 + b 2 . Let's build the triangle to a square with side a+b, as shown in the figure (Fig. 9 b).
The area of such a square with side a + b is equal to (a + b) 2. On the other hand, this square is made up of four equal right triangles with area ab and a square with side c, so
Thus, (a + b) 2 =2ab + c 2, whence c 2 = a 2 + b 2.
Q.E.D.
COROLLARY 1 . In a right triangle, any of the legs is less than the hypotenuse.
PROOF. According to the Pythagorean theorem AB 2 = AC 2 + BC 2 . Since BC 2 >0, then AC 2<АВ, То есть АС<АВ.
CONCLUSION 2. For any acute angle b cosb<1.
EVIDENCE. By definition of cosine cosб = . But in Corollary 1 it was proven that AC<АВ, This means the fraction is less than 1.
Right triangles whose sides are expressed as integers are called Pythagorean triangles.
It can be proven that the legs a, b and hypotenuse c of such triangles are expressed by the formulas a=2kmn; b=k(m 2 -n 2); c=k(m 2 +n 2), where k, m and n are natural numbers such that m>n. Triangles with sides whose lengths are 3, 4, 5 are called Egyptian triangles, because they were known to the ancient Egyptians.
Converse to the Pythagorean theorem.
If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is right-angled (a sign of a right triangle).
PROOF.
Let in triangle ABC AB 2 = AC 2 + BC 2. Let us prove that angle C is a right angle. Consider a right triangle A 1 B 1 C 1 with right angle C 1, in which A 1 C 1 = AC and B 1 C 1 = BC. By the Pythagorean theorem A 1 B 1 2 =A 1 C 1 2 +B 1 C 1 2, and therefore A 1 B 1 2 = AC 2 +BC 2. But AC 2 + BC 2 = AB 2 according to the theorem. Therefore, A 1 B 1 2 = AB 2, whence A 1 B 1 = AB. Triangles ABC and A 1 B 1 C 1 are equal on three sides, therefore< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.
Q.E.D.
Right triangles, along with isosceles and equilateral triangles, take their place among triangles, possessing a special set of specific properties characteristic only of this type of triangle. Let's consider several theorems on the equality of right triangles, which will significantly simplify the solution of some problems.
The first sign of equality of right triangles
The signs of equality of right triangles stem from the three signs of equality of triangles, but a right angle distorts them, expanding them while making them simpler. Any of the signs of equality of right triangles can be replaced by one of the three main ones, but this will take too much time, so 5 properties and signs of equality of right triangles have been identified.
Very often, instead of using the basic signs of equality of triangles, the superposition method is used, when two figures are mentally superimposed on one another. It cannot be said that this is true or false. Just another method of proof to consider. But one cannot think that any sign can be proven by ordinary superposition. That is why we will consider the proof of the signs of equality of right triangles through the three main signs of equality of triangles.
The first sign of equality of right triangles says: two right triangles are equal if two legs of one triangle are equal to two legs of another triangle. In short, this feature is called equality on two sides.

Rice. 1. Equality on two sides
Proving this sign is very simple. Given: two legs of a right triangle are equal. Between the legs there is a right angle, which is equal to 90 degrees, which means that the angle of the triangles coincides. Therefore, two triangles are equal in two sides and the angle between them.
Second sign
The second sign reads like this: two right triangles are equal if the leg and the adjacent acute angle of one triangle are equal to the leg and the adjacent angle of the other triangle.
The second sign is proven based on the same statement about the equality of right angles with each other. If triangles have equal legs, their acute angles are equal, and right angles are equal by definition, then such triangles are equal according to the second sign of equality (side and two adjacent angles).
Third sign
Two right triangles are congruent if the side and the opposite acute angle are equal.

Rice. 2. Drawing for proof
The sum of the acute angles in a triangle is 90 degrees. Let us denote the angles in small Latin letters for simplicity of proof. One angle is right, and the other two are designated by the letters a and b in the first triangle; c and d in the second triangle.
Angles a and d are equal to each other according to the conditions of the problem.
Subtract angle a from both sides of the expression
That is, if in two right triangles two acute angles are equal to each other, then the other two acute angles will also be equal, and we can use the second sign.
In the second and third signs, you need to especially focus on the acute angle, since right angles are always equal to each other.
Fourth sign
If the hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent.
As stated in the previous sign: if an acute angle of a right triangle is equal to the corresponding acute angle of another right triangle, then the other pair of acute angles of triangles will be equal to each other.
This means that, according to the conditions of this criterion, we have equality of the hypotenuse and two acute angles of triangles, which means such triangles will be equal in side and two adjacent angles (2nd sign of equality of triangles)
Fifth sign
If the hypotenuse and leg of one right triangle are respectively equal to the hypotenuse and leg of another triangle, then such triangles are congruent.
If the hypotenuse and leg of two triangles are respectively equal, then the second legs of such triangles will be equal to each other. This stems from the Pythagorean theorem.

Rice. 3. Equality along the leg and hypotenuse
The square of the hypotenuse is equal to the sum of the squares of the legs. The hypotenuses are equal to each other, the leg of one triangle is equal to the square of the other triangle, which means that the sum remains true, and the other two legs will be equal to each other.
What have we learned?
We looked at the proof of the five tests for the equality of triangles through the basic tests for the equality of triangles. We figured out why such a proof is preferable to an overlay and determined a proof path that will allow you to restore the basic concepts of the topic in memory at any time, without unnecessary memorization.
Test on the topic
Article rating
Average rating: 4.6. Total ratings received: 100.
Let us recall from the material in the previous lesson that a triangle is called a right triangle if at least one of its angles is a right angle (i.e. equal to 90°).
Let's consider first sign Equality of triangles: if two legs of one right triangle are respectively equal to two legs of another right triangle, then such triangles are congruent.
Let's illustrate this case:
Rice. 1. Equal right triangles
Proof:
Let us recall the first equality of arbitrary triangles.

Rice. 2
If two sides and the angle between them of one triangle and the corresponding two sides and the angle between them of the second triangle are equal, then these triangles are congruent. This is indicated by the first sign of equality of triangles, that is:

A similar proof follows for right triangles:
 .
.
Triangles are equal according to the first criterion.
Let's consider the second sign of equality of right triangles. If the leg and the adjacent acute angle of one right triangle are respectively equal to the leg and the adjacent acute angle of another right triangle, then such triangles are congruent.

Rice. 3
Proof:

Rice. 4
Let's use the second criterion for the equality of triangles:

Similar proof for right triangles:

Triangles are equal according to the second criterion.
Let's consider the third criterion for the equality of right triangles: if the hypotenuse and the adjacent angle of one right triangle are respectively equal to the hypotenuse and the adjacent angle of another triangle, then such triangles are congruent.
Proof:

Rice. 5
Let us recall the second criterion for the equality of triangles:

Rice. 6
These triangles are equal if:

Since it is known that one pair of acute angles in right triangles is equal to (∠A = ∠A 1), then the equality of the other pair of angles (∠B = ∠B 1) is proven as follows:
Since AB = A 1 B 1 (by condition), ∠B = ∠B 1, ∠A = ∠A 1. Therefore, triangles ABC and A 1 B 1 C 1 are equal according to the second criterion.
Consider the following criterion for the equality of triangles:
If the leg and hypotenuse of one triangle are respectively equal to the leg and hypotenuse of another triangle, such right triangles are congruent.

Rice. 7
Proof:
Let's combine triangles ABC and A 1 B 1 C 1 by overlapping. Let us assume that vertices A and A 1, as well as C and C 1 are superimposed, but vertex B and point B 1 do not coincide. This is exactly the case shown in the following figure:

Rice. 8
In this case, we can notice the isosceles triangle ABV 1 (by definition - by the condition AB = AB 1). Therefore, according to the property, ∠AB 1 B = ∠ABV 1. Let's look at the definition of an external angle. External corner of a triangle is the angle adjacent to any angle of the triangle. Its degree measure is equal to the sum of two angles of a triangle that are not adjacent to it. The figure shows this ratio:

Rice. 9
Angle 5 is the external angle of the triangle and is equal to ∠5 = ∠1 + ∠2. It follows that an external angle is greater than each of the angles non-adjacent to it.
Thus, ∠ABB 1 is the external angle for triangle ABC and is equal to the sum ∠ABB 1 = ∠CAB + ∠ACB = ∠ABC = ∠CAB + 90 o. Thus, ∠AB 1 B (which is an acute angle in the right triangle ABC 1) cannot be equal to the angle ∠ABB 1, because this angle is obtuse according to what has been proven.
This means that our assumption regarding the location of points B and B 1 turned out to be incorrect, therefore these points coincide. This means that triangles ABC and A 1 B 1 C 1 are superimposed. Therefore they are equal (by definition).
Thus, these features are not introduced in vain, because they can be used to solve some problems.
- Omsk State University ().
- Help portal calc.ru ().
- Teacher portal ().
1. No. 38. Butuzov V.F., Kadomtsev S.B., Prasolov V.V., edited by Sadovnichy V.A. Geometry 7. M.: Education. 2010
2. Based on the data indicated in the figure, indicate equal triangles, if any.

3. Based on the data indicated in the figure, indicate equal triangles, if any. Keep in mind that AC = AF.

4. In a right triangle, the median and altitude are drawn to the hypotenuse. The angle between them is 20 o. Determine the size of each of the acute angles of this right triangle.
Sections: Mathematics
Topic: “Signs for the equality of right triangles”
Goal: consolidation of knowledge (properties of right triangles), familiarization with some signs of equality of right triangles.
During the classes:
I. Organizational moment.II. Orally.
1. Answer the questions:
- Name the elements of a right triangle.
- What properties do the elements of a right triangle have?
- Prove that the leg of a right triangle lying opposite an angle of 30 0 is equal to half the hypotenuse.
- Prove that if a leg of a right triangle is equal to half the hypotenuse, then the angle opposite this leg is equal to 30 0.
- Find x. Choose the answer from the triangle. The letters of a word are located in the sectors of the triangle. Discussion in pairs (3 min).
Picture 1.
They made up the word “sign”.
III. Learning new materialBy studying triangles, we say that it has certain properties and characteristics. What signs of equality of triangles do you know? We have formulated and proved the properties of right triangles, and today we will look at the signs of equality of right triangles and solve problems using them.
When proving the equality of triangles, how many pairs of correspondingly equal elements were found? Is it possible to prove the equality of right triangles along two sides?
In front of you are two right triangles ABC and A 1 B 1 C 1, their legs are respectively equal. Prove, if possible, their equality.
No. 1. (On two sides)

Figure 2.
Given: ABC and A 1 B 1 C 1, B=B 1 =90 0, AB = A 1 B 1, BC = B 1 C 1
Prove: ABC = A 1 B 1 C 1
What will the sign sound like? (Then task No. 1)
No. 2. (According to the leg and the acute angle adjacent to it)

Figure 3.
Given: ABC and A 1 B 1 C 1, B=B 1 =90 0, BC = B 1 C 1, C= C 1
Prove: ABC = A 1 B 1 C 1
What will the sign sound like? (Then task No. 2)
No. 3. (By hypotenuse and acute angle)

Figure 4.
Given: ABC and A 1 B 1 C 1, B=B 1 =90 0, AC = A 1 C 1, A= A 1
Prove: ABC = A 1 B 1 C 1
What will the sign sound like? (Then task No. 3)
Tasks. Find congruent triangles and prove their equality.

Figure 5.
IV. Reinforcing what has been learned in the lesson.Solve the following problem.

Figure 6.
Given: ABC, A 1 B 1 C 1, DAB=CBA=90 0, AD = BD
Prove: CAB=DBA.
Discussion in groups of four (3 min).
Why problem from textbook No. 261 with recording.

Figure 7.
Given: ABC – isosceles, AD and CE – height of ABC
Prove: AD = CE
Proof:
V. Homework assignment.
P.35 (three signs), No. 261 (prove that AOS is isosceles), No. 268 (test for the equality of right triangles along a leg and an opposite angle).
In the next geometry lesson we will continue our acquaintance with the signs of equality of right triangles. I will also give marks next time based on the results for 2 lessons.
Additionally. Find equal triangles.