Determination of the intersection of a line and a plane. Scientific electronic library. Special cases of mutual parallelism and perpendicularity of a line and a plane. special cases of mutual perpendicularity of two planes

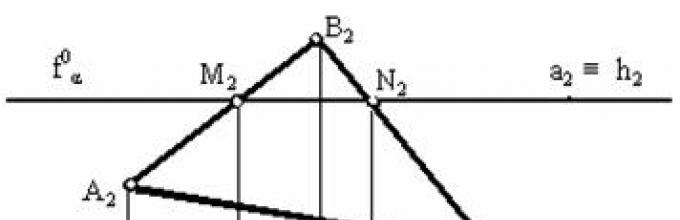
The line of intersection of two planes is a straight line. Let us first consider the special case (Fig. 3.9), when one of the intersecting planes is parallel to the horizontal plane of projections (α π 1, f 0 α X). In this case, the line of intersection a, belonging to the planeα, will also be parallel to the plane π 1, (Fig. 3.9. a), that is, it will coincide with the horizontal of the intersecting planes (a ≡ h).

If one of the planes is parallel to the frontal plane of projections (Fig. 3.9. b), then the intersection line a belonging to this plane will be parallel to the plane π 2 and will coincide with the frontal of the intersecting planes (a ≡ f).

.

.

Rice. 3.9. Special case plane intersections general position with planes: a - horizontal level; b - frontal level

An example of constructing the point of intersection (K) of straight line a (AB) with plane α (DEF) is shown in Fig. 3.10. To do this, straight line a is enclosed in an arbitrary plane β and the intersection line of planes α and β is determined.

In the example under consideration, straight lines AB and MN belong to the same plane β and intersect at point K, and since straight line MN belongs to a given plane α (DEF), point K is also the point of intersection of straight line a (AB) with plane α. (Fig. 3.11).

.

Rice. 3.10. Constructing the point of intersection of a line and a plane

To solve such a problem in a complex drawing, you must be able to find the point of intersection of a straight line in general position with a plane in general position.

Let's consider an example of finding the point of intersection of straight line AB with the plane of triangle DEF shown in Fig. 3.11.

To find the intersection point through the frontal projection of line A 2 B 2, a frontally projecting plane β was drawn which intersected the triangle at points M and N. On the frontal plane of projections (π 2), these points are represented by projections M 2, N 2. From the condition of belonging to a straight plane on the horizontal plane of projections (π 1), horizontal projections of the resulting points M 1 N 1 are found. At the intersection of the horizontal projections of lines A 1 B 1 and M 1 N 1, a horizontal projection of their intersection point (K 1) is formed. According to the line of communication and the conditions of membership on the frontal plane of projections, there is a frontal projection of the intersection point (K 2).

.

Rice. 3.11. An example of determining the intersection point of a line and a plane

The visibility of segment AB relative to triangle DEF is determined by the competing point method.

On the plane π 2 two points NEF and 1AB are considered. Based on the horizontal projections of these points, it can be established that point N is located closer to the observer (Y N >Y 1) than point 1 (the direction of the line of sight is parallel to S). Consequently, the straight line AB, i.e. part of the straight line AB (K 1) is covered by the plane DEF on the plane π 2 (its projection K 2 1 2 is shown by the dashed line). Visibility on the π 1 plane is established similarly.

Questions for self-control

1) What is the essence of the competing point method?

2) What properties of a straight line do you know?

3) What is the algorithm for determining the intersection point of a line and a plane?

4) What tasks are called positional?

5) Formulate the conditions for belonging to a straight plane.

We bring to your attention magazines published by the publishing house "Academy of Natural Sciences"

It is known that a straight line intersects a plane if it does not belong to this plane and is not parallel to it. Following the algorithm below, we find the point of intersection of the line a with a generic plane α defined by the traces h 0α , f 0α .

Algorithm

1. Via direct a we draw an auxiliary frontally projecting plane γ. The figure shows its traces h 0γ, f 0γ.
2. We construct projections of straight line AB along which planes α and γ intersect. In this problem, point B" = h 0α ∩ h 0γ, A"" = f 0α ∩ f 0γ. Points A" and B"" lie on the x-axis, their position is determined by the communication lines.
3. Direct a and AB intersect at the desired point K. Its horizontal projection K" = a" ∩ A"B". The frontal projection K"" lies on the straight line a"".

The solution algorithm will remain the same if pl. α will be given by parallel, crossing lines, a section of a figure, or other possible means.

Visibility of line a relative to plane α. Competing Points Method

1. Let us mark the frontal-competing points A and C in the drawing (Fig. below). We will assume that point A belongs to the area. α, and C lies on the line a. The frontal projections A"" and C"" coincide, but at the same time points A and C are removed from the plane of projections P 2 at different distances.
2. Let's find the horizontal projections A" and C". As can be seen in the figure, point C" is removed from plane P 2 at a greater distance than point A", which belongs to the square. α. Consequently, a section of straight line a"", located to the left of point K"", will be visible. Section a"" to the right of K"" is invisible. We mark it with a dashed line.
3. Let us mark horizontally competing points D and E in the drawing. We will assume that point D belongs to the square. α, and E lies on the line a. Horizontal projections D" and E" coincide, but at the same time points D and E are removed from the plane P 1 at different distances.
4. Let us determine the position of the frontal projections D"" and E"". As can be seen in the figure, point D"", located in the square. α, is removed from the plane P 1 at a greater distance than point E "", belonging to straight line a. Consequently, section a" located to the right of point K" will be invisible. We mark it with a dashed line. Section a" to the left of K" is visible.

Given a straight line: (1) and a plane: Ax + By + Cz + D = 0 (2).

Let's find the coordinates of the point of intersection of the line and the plane. If straight line (1) and plane (2) intersect, then the coordinates of the intersection point satisfy equations (1) and (2):

, .

Substituting the found value of t into (1), we obtain the coordinates of the intersection point.

1) If Am + Bn + Cp = 0, and Ax 0 + By 0 + Cz 0 + D ≠ 0, then t does not exist, i.e. a straight line and a plane do not have a single common point. They are parallel.

2) Am + Bn + Cp = 0 and Ax 0 + By 0 + Cz 0 + D = 0. In this case, t can take any values ​​and , i.e. a straight line is parallel to the plane and has common point, i.e. it lies in a plane.

Example 1. Find the point of intersection of a line with plane 3x – 3y + 2z – 5 = 0.

3(2t – 1) – 3(4t + 3) + 2 3t – 5 = 0 => -17=0, which is impossible for any t, i.e. a straight line and a plane do not intersect.

Example 2. Find the point of intersection of a line and planes: x + 2y – 4z + 1 = 0.

8t + 13 + 2(2t + 1) – 4(3t + 4) + 1 = 0, 0 + 0 = 0. This is true for any value of t, i.e. the straight line lies in the plane.

Example 3. Find the point of intersection of a line and plane 3x – y + 2z – 5 = 0.

3(5t + 7) – t – 4 + 2(4t + 5) – 5 = 0, 22t + 22 = 0, t = -1, x = 5(-1) + 7 = 2, y = -1 + 4 = 3, z = 4(-1) + 5 = 1, M(2, 3, 1) – the point of intersection of the line and the plane.

The angle between a straight line and a plane. Conditions for parallelism and perpendicularity of a straight line and a plane.

The angle between a straight line and a plane is called sharp corner q between a straight line and its projection onto a plane.

Let a straight line and a plane be given:

And .

Let the straight line intersect the plane and form an angle μ () with it. Then b = 90 0 – q or b = 90 0 + q is the angle between the normal vector of the plane and the directing vector of the straight line. But . Means

(3).

a) If L P, then - the condition of perpendicularity of a straight line and a plane.

b) If L||P, then is the condition for parallelism of the line and the plane.

c) If the line is L||P and at the same time the point M0(x0, y0, z0) P, then the line lies in this plane. Analytically:

- conditions for belonging to a straight line and a plane.

Example. Given a straight line and point M 0 (1, 0, –2). Through point M 0 draw a plane perpendicular to this line. We look for the equation of the desired plane in the form: A(x – 1) + B(y – 0) + C(z + 2) = 0. In this case , ,

5(x – 1) – 5y + 5(z + 2) = 0, - x – y + z + 3 = 0.

A bunch of planes.

A beam of planes is the set of all planes passing through a given straight line—the axis of the beam.

To define a bundle of planes, it is enough to specify its axis. Let the equation of this line be given in general form:

.

To compose a beam equation means to compose an equation from which one can obtain additional condition equation of any plane of the beam, except, b.m. one. Let's multiply equation II by l and add it to equation I:

A 1 x + B 1 y + C 1 z + D 1 + l(A 2 x + B 2 y + C 2 z + D 2) = 0 (1) or

(A 1 + lA 2)x + (B 1 + lB 2)y + (C 1 + lC 2)z + (D 1 + lD 2) = 0 (2).

l – parameter – a number that can take real values. For any chosen value of l, equations (1) and (2) are linear, i.e. these are the equations of a certain plane.

1. Let us show that this plane passes through the beam axis L. Take an arbitrary point M 0 (x 0, y 0, z 0) L. Consequently, M 0 P 1 and M 0 P 2. Means:

3x – y + 2z + 9 + 17x + 17z – 51 = 0; 20x – y + 19z – 42 = 0.

Example 3 (E). Write an equation for a plane passing through a line perpendicular to the plane x – 2y + z + 5 = 0. ; 3x – 2y + z – 3 + l(x – 2z) = 0; (3 + l)x – 2y + (1 – 2 l)z – 3 = 0; ; ; l = 8; 11x – 2y – 15z – 3 = 0.

77*. Find the point of intersection of straight line AB with the plane defined by triangle CDE (Fig. 75, a).

Solution. As is known, to find the point of intersection of a straight line with a general plane, one should draw an auxiliary plane (R) through the straight line, construct a line of intersection of this plane with a given one (1-2) and find

the point of intersection (K) of the given and constructed lines. Point K is the desired point of intersection of the line with the plane (Fig. 75, b). A horizontal or frontal projection plane is usually used as an auxiliary plane.

In Fig. 75, in c, a frontally projecting plane R is drawn through the straight line AB, its trace R ϑ coincides with a "c". horizon. The trace of the plane is not needed in this problem and is therefore not shown.

We construct the line of intersection of the plane R and the plane defined by the triangle CDE (for an example of such a construction, see Problem 67). Having constructed line 1-2 (Fig. 75, c), we find the point of intersection of it with straight line AB - point K (k, k").

To determine the sections of line AB that will be covered by a triangle, you should use an analysis of the position of points on intersecting lines.

For example, points 1 and 3 are on the intersecting lines (respectively) ED and AB. The frontal projections of these points coincide, i.e. points 1 and 3 are equally distant from the square. N. But their distances from the square. V are different: point 3 is further from the square. V than point 1. Therefore, in relation to pl. V point 3 covers point 1 (the direction of view is indicated by the arrow S). Consequently, straight line AB passes in front of triangle CDE to point K. Starting from point K to the left, straight line AB is covered by a triangle, and therefore this section of the straight line is shown by a dashed line.

To identify an invisible area on the horizon. projections of straight line AB, consider points 4 and 5, lying respectively on straight lines AB and CD.

If we look at these points in the direction s 1, we first see point 5. Point 4 is covered by point 5. Consequently, line AB in this place is covered by triangle CDE, and the section of its projection from point k to point 4 should be shown by a dashed line. In this case, point K was inside the contour of triangle CDE.

If the relative position of the intersecting elements is different, it is possible that point K will be outside the triangle (Fig. 75, d). This means that line AB intersects the plane defined by triangle CDE outside the contour of this triangle. AB becomes invisible behind point K (to the left).

78. Find the points of intersection of straight line AB with the faces of the pyramid (Fig. 76). The faces of the pyramid should be considered as planes defined by triangles.

79. Find the points of intersection of straight line AB with the faces of the prism (Fig. 77). The faces of the prism should be considered as planes defined by parallel straight lines.

80*. Find the points of intersection of straight line AB with plane P (Fig. 78, a).

Solution. We draw the frontally projecting plane R through the straight line AB (Fig. 78, biv) (its trace R ϑ coincides with a "b") and construct the line MN of the intersection of both planes - given and drawn through AB (the construction is similar to that performed in problem 70). The required point K(k, k") of intersection of straight line AB with plane P is located at the point of intersection of MN with AB.

In this problem, the visibility of the straight section from point A to K is obvious; however, more difficult cases the visible section of the straight line should be determined based on

analysis of the position of points. For example, taking point 1 (on line AB) and point N (on trace P ϑ). we see that point 1 is located further relative to the square. V than point N. Therefore, straight line AB to point K is visible. Beyond point K, the straight line is shown as a dashed line and is invisible. Visibility to the horizon is determined similarly. projections.

81. Find the point of intersection of straight line AB with plane P (Fig. 79).

82*. Find the point of intersection of straight line AB with plane P (Fig. 80, a).

Solution. Through straight line AB we draw a horizontally projecting plane R (the trace of R h coincides with ab) and construct the line of intersection of planes P and R,

using the points M and N of the intersection of their tracks of the same name (Fig. 80, b and c). The desired point (k", k) is located at the intersection point of MN with AB. In Fig. 80, d, point K is constructed using plot W. Since plot P is profile-projecting (Fig. 80, b).

then the profile projection k" lies at the point of intersection of the trace P ω with a"b". Knowing k", we construct k" on a"b" and k on ab. The visible sections of the straight line AB are determined in the same way as in problems 77 and 80.

83. Find the point of intersection of straight line AB with plane P (Fig. 81).

84*. Find the point of intersection of straight line AB with the plane defined by triangle CDE (Fig. 82, a).

Solution. Through straight line AB we draw (Fig. 82, b and c) square. R, parallel to the square W. She crosses given plane along the straight line MN (points m", n", m and n lie at the intersection of the traces R ϑ and R h with the same projections of the corresponding sides

triangle CDE). Since the lines AB and MN are profile, to find the point (K) of their intersection we construct profile projections a"b" and m"n". The projection k" is located at the intersection of a"b" and m"m". Using k" we construct k" on a"b" and k on ab.

85. Find the point of intersection of straight line EF with the plane defined by the quadrilateral ABCD (Fig. 83).