Dot product i j. Formula for the scalar product of vectors for plane problems. Solve the problem yourself and then see the solution

Angle between vectors

Consider two given vectors $\overrightarrow(a)$ and $\overrightarrow(b)$. Let us subtract the vectors $\overrightarrow(a)=\overrightarrow(OA)$ and $\overrightarrow(b)=\overrightarrow(OB)$ from an arbitrarily chosen point $O$, then the angle $AOB$ is called the angle between the vectors $\overrightarrow( a)$ and $\overrightarrow(b)$ (Fig. 1).

Figure 1.

Note here that if the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ are codirectional or one of them is the zero vector, then the angle between the vectors is $0^0$.

Notation: $\widehat(\overrightarrow(a),\overrightarrow(b))$

The concept of dot product of vectors

Mathematically, this definition can be written as follows:

The dot product can be zero in two cases:

If one of the vectors is a zero vector (Since then its length is zero).

If the vectors are mutually perpendicular (that is, $cos(90)^0=0$).

Note also that the scalar product is greater than zero if the angle between these vectors is acute (since $(cos \left(\widehat(\overrightarrow(a),\overrightarrow(b))\right)\ ) >0$), and less than zero if the angle between these vectors is obtuse (since $(cos \left(\widehat(\overrightarrow(a),\overrightarrow(b))\right)\ )

Related to the concept of a scalar product is the concept of a scalar square.

Definition 2

The scalar square of a vector $\overrightarrow(a)$ is the scalar product of this vector with itself.

We find that the scalar square is equal to

Calculating the dot product from vector coordinates

In addition to the standard way of finding the value of the scalar product, which follows from the definition, there is another way.

Let's consider it.

Let the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ have coordinates $\left(a_1,b_1\right)$ and $\left(a_2,b_2\right)$, respectively.

Theorem 1

The scalar product of the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ is equal to the sum of the products of the corresponding coordinates.

Mathematically this can be written as follows

\[\overrightarrow(a)\overrightarrow(b)=a_1a_2+b_1b_2\]

Proof.

The theorem has been proven.

This theorem has several consequences:

Corollary 1: Vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ are perpendicular if and only if $a_1a_2+b_1b_2=0$

Corollary 2: The cosine of the angle between the vectors is equal to $cos\alpha =\frac(a_1a_2+b_1b_2)(\sqrt(a^2_1+b^2_1)\cdot \sqrt(a^2_2+b^2_2))$

Properties of the scalar product of vectors

For any three vectors and a real number $k$ the following is true:

$(\overrightarrow(a))^2\ge 0$

This property follows from the definition of a scalar square (Definition 2).

Travel law:$\overrightarrow(a)\overrightarrow(b)=\overrightarrow(b)\overrightarrow(a)$.

This property follows from the definition of the scalar product (Definition 1).

Distributive law:

$\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)$. \end(enumerate)

By Theorem 1, we have:

\[\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\left(a_1+a_2\right)a_3+\left(b_1+b_2\right)b_3=a_1a_3+a_2a_3+ b_1b_3+b_2b_3==\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)\]

Combination law:$\left(k\overrightarrow(a)\right)\overrightarrow(b)=k(\overrightarrow(a)\overrightarrow(b))$. \end(enumerate)

By Theorem 1, we have:

\[\left(k\overrightarrow(a)\right)\overrightarrow(b)=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow(a)\overrightarrow(b))\]

An example of a problem for calculating the scalar product of vectors

Example 1

Find the scalar product of the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ if $\left|\overrightarrow(a)\right|=3$ and $\left|\overrightarrow(b)\right|= 2$, and the angle between them is $((30)^0,\ 45)^0,\ (90)^0,\ (135)^0$.

Solution.

Using Definition 1, we get

For $(30)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((30)^0\right)\ )=6\cdot \frac(\sqrt(3))(2)=3\sqrt( 3)\]

For $(45)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((45)^0\right)\ )=6\cdot \frac(\sqrt(2))(2)=3\sqrt( 2)\]

For $(90)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((90)^0\right)\ )=6\cdot 0=0\]

For $(135)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((135)^0\right)\ )=6\cdot \left(-\frac(\sqrt(2))(2)\ right)=-3\sqrt(2)\]

If in the problem both the lengths of the vectors and the angle between them are presented “on a silver platter,” then the condition of the problem and its solution look like this:

Example 1. Vectors are given. Find the scalar product of vectors if their lengths and the angle between them are represented by the following values:

Another definition is also valid, completely equivalent to definition 1.

Definition 2. The scalar product of vectors is a number (scalar) equal to the product of the length of one of these vectors and the projection of another vector onto the axis determined by the first of these vectors. Formula according to definition 2:

We will solve the problem using this formula after the next important theoretical point.

Definition of the scalar product of vectors in terms of coordinates

The same number can be obtained if the vectors being multiplied are given their coordinates.

Definition 3. The dot product of vectors is a number equal to the sum of the pairwise products of their corresponding coordinates.

On a plane

If two vectors and on the plane are defined by their two Cartesian rectangular coordinates

then the scalar product of these vectors is equal to the sum of pairwise products of their corresponding coordinates:

Example 2. Find the numerical value of the projection of the vector onto the axis parallel to the vector.

Solution. We find the scalar product of vectors by adding the pairwise products of their coordinates:

Now we need to equate the resulting scalar product to the product of the length of the vector and the projection of the vector onto an axis parallel to the vector (in accordance with the formula).

We find the length of the vector as the square root of the sum of the squares of its coordinates:

We create an equation and solve it:

Answer. The required numerical value is minus 8.

In space

If two vectors and in space are defined by their three Cartesian rectangular coordinates

then the scalar product of these vectors is also equal to the sum of pairwise products of their corresponding coordinates, only there are already three coordinates:

The task of finding the scalar product using the considered method is after analyzing the properties of the scalar product. Because in the problem you will need to determine what angle the multiplied vectors form.

Properties of the scalar product of vectors

Algebraic properties

1. (commutative property: reversing the places of the multiplied vectors does not change the value of their scalar product).

2. (associative property with respect to a numerical factor: the scalar product of a vector multiplied by some factor and another vector is equal to the scalar product of these vectors multiplied by the same factor).

3. (distributive property relative to the sum of vectors: the scalar product of the sum of two vectors by the third vector is equal to the sum of the scalar products of the first vector by the third vector and the second vector by the third vector).

4. (scalar square of vector greater than zero), if is a nonzero vector, and , if is a zero vector.

Geometric properties

In the definitions of the operation under study, we have already touched on the concept of an angle between two vectors. It's time to clarify this concept.

In the figure above you can see two vectors that are brought to a common origin. And the first thing you need to pay attention to is that there are two angles between these vectors - φ 1 And φ 2 . Which of these angles appears in the definitions and properties of the scalar product of vectors? The sum of the considered angles is 2 π and therefore the cosines of these angles are equal. The definition of a dot product includes only the cosine of the angle, and not the value of its expression. But the properties only consider one angle. And this is the one of the two angles that does not exceed π , that is, 180 degrees. In the figure this angle is indicated as φ 1 .

1. Two vectors are called orthogonal And the angle between these vectors is straight (90 degrees or π /2 ), if the scalar product of these vectors is zero :

Orthogonality in vector algebra is the perpendicularity of two vectors.

2. Two non-zero vectors make up acute angle (from 0 to 90 degrees, or, which is the same - less π dot product is positive .

3. Two non-zero vectors make up obtuse angle (from 90 to 180 degrees, or, what is the same - more π /2) if and only if they dot product is negative .

Example 3. The coordinates are given by the vectors:

Calculate the scalar products of all pairs of given vectors. What angle (acute, right, obtuse) do these pairs of vectors form?

Solution. We will calculate by adding the products of the corresponding coordinates.

We got a negative number, so the vectors form an obtuse angle.

We got a positive number, so the vectors form an acute angle.

We got zero, so the vectors form a right angle.

We got a positive number, so the vectors form an acute angle.

For self-test you can use online calculator Dot product of vectors and cosine of the angle between them .

Example 4. Given the lengths of two vectors and the angle between them:

Determine at what value of the number the vectors and are orthogonal (perpendicular).

Solution. Let's multiply the vectors using the rule for multiplying polynomials:

Now let's calculate each term:

Let’s create an equation (the product is equal to zero), add similar terms and solve the equation:

Answer: we got the value λ = 1.8, at which the vectors are orthogonal.

Example 5. Prove that the vector orthogonal (perpendicular) to the vector

Solution. To check orthogonality, we multiply the vectors and as polynomials, substituting instead the expression given in the problem statement:

To do this, you need to multiply each term (term) of the first polynomial by each term of the second and add the resulting products:

In the resulting result, the fraction is reduced by. The following result is obtained:

Conclusion: as a result of multiplication we got zero, therefore, the orthogonality (perpendicularity) of the vectors is proven.

Solve the problem yourself and then see the solution

Example 6. The lengths of the vectors and are given, and the angle between these vectors is π /4. Determine at what value μ vectors and are mutually perpendicular.

For self-test you can use online calculator Dot product of vectors and cosine of the angle between them .

Matrix representation of the dot product of vectors and the product of n-dimensional vectors

Sometimes it is advantageous for clarity to represent two multiplied vectors in the form of matrices. Then the first vector is represented as a row matrix, and the second as a column matrix:

Then the scalar product of vectors will be the product of these matrices :

The result is the same as that obtained by the method we have already considered. We got one single number, and the product of a row matrix by a column matrix is also one single number.

It is convenient to represent the product of abstract n-dimensional vectors in matrix form. Thus, the product of two four-dimensional vectors will be the product of a row matrix with four elements by a column matrix also with four elements, the product of two five-dimensional vectors will be the product of a row matrix with five elements by a column matrix also with five elements, and so on.

Example 7. Find scalar products of pairs of vectors

using matrix representation.

Solution. The first pair of vectors. We represent the first vector as a row matrix, and the second as a column matrix. We find the scalar product of these vectors as the product of a row matrix and a column matrix:

We similarly represent the second pair and find:

As you can see, the results were the same as for the same pairs from example 2.

Angle between two vectors

The derivation of the formula for the cosine of the angle between two vectors is very beautiful and concise.

To express the dot product of vectors

(1)

in coordinate form, we first find the scalar product of the unit vectors. The scalar product of a vector with itself by definition:

What is written in the formula above means: the scalar product of a vector with itself is equal to the square of its length. The cosine of zero is equal to one, so the square of each unit will be equal to one:

Since vectors

are pairwise perpendicular, then the pairwise products of the unit vectors will be equal to zero:

Now let's perform the multiplication of vector polynomials:

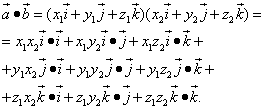
We substitute the values of the corresponding scalar products of the unit vectors into the right side of the equality:

We obtain the formula for the cosine of the angle between two vectors:

Example 8. Three points are given A(1;1;1), B(2;2;1), C(2;1;2).

Find the angle.

Solution. Finding the coordinates of the vectors:

Using the cosine angle formula we get:

Hence, .

For self-test you can use online calculator Dot product of vectors and cosine of the angle between them .

Example 9. Two vectors are given

Find the sum, difference, length, dot product and angle between them.

2.Difference

Angle between vectors

Figure 1.

Note here that if the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ are codirectional or one of them is the zero vector, then the angle between the vectors is $0^0$.

Notation: $\widehat(\overrightarrow(a),\overrightarrow(b))$

The concept of dot product of vectors

Mathematically, this definition can be written as follows:

The dot product can be zero in two cases:

If one of the vectors is a zero vector (Since then its length is zero).

If the vectors are mutually perpendicular (that is, $cos(90)^0=0$).

Related to the concept of a scalar product is the concept of a scalar square.

Definition 2

The scalar square of a vector $\overrightarrow(a)$ is the scalar product of this vector with itself.

We find that the scalar square is equal to

Calculating the dot product from vector coordinates

In addition to the standard way of finding the value of the scalar product, which follows from the definition, there is another way.

Let's consider it.

Let the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ have coordinates $\left(a_1,b_1\right)$ and $\left(a_2,b_2\right)$, respectively.

Theorem 1

The scalar product of the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ is equal to the sum of the products of the corresponding coordinates.

Mathematically this can be written as follows

\[\overrightarrow(a)\overrightarrow(b)=a_1a_2+b_1b_2\]

Proof.

The theorem has been proven.

This theorem has several consequences:

Corollary 1: Vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ are perpendicular if and only if $a_1a_2+b_1b_2=0$

Corollary 2: The cosine of the angle between the vectors is equal to $cos\alpha =\frac(a_1a_2+b_1b_2)(\sqrt(a^2_1+b^2_1)\cdot \sqrt(a^2_2+b^2_2))$

Properties of the scalar product of vectors

For any three vectors and a real number $k$ the following is true:

$(\overrightarrow(a))^2\ge 0$

This property follows from the definition of a scalar square (Definition 2).

Travel law:$\overrightarrow(a)\overrightarrow(b)=\overrightarrow(b)\overrightarrow(a)$.

This property follows from the definition of the scalar product (Definition 1).

Distributive law:

$\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)$. \end(enumerate)

By Theorem 1, we have:

Combination law:$\left(k\overrightarrow(a)\right)\overrightarrow(b)=k(\overrightarrow(a)\overrightarrow(b))$. \end(enumerate)

By Theorem 1, we have:

\[\left(k\overrightarrow(a)\right)\overrightarrow(b)=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow(a)\overrightarrow(b))\]

An example of a problem for calculating the scalar product of vectors

Example 1

Solution.

Using Definition 1, we get

For $(30)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((30)^0\right)\ )=6\cdot \frac(\sqrt(3))(2)=3\sqrt( 3)\]

For $(45)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((45)^0\right)\ )=6\cdot \frac(\sqrt(2))(2)=3\sqrt( 2)\]

For $(90)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((90)^0\right)\ )=6\cdot 0=0\]

For $(135)^0:$

\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((135)^0\right)\ )=6\cdot \left(-\frac(\sqrt(2))(2)\ right)=-3\sqrt(2)\]

Lecture: Vector coordinates; scalar product of vectors; angle between vectors

Vector coordinates

So, as mentioned earlier, a vector is a directed segment that has its own beginning and end. If the beginning and end are represented by certain points, then they have their own coordinates on a plane or in space.

If each point has its own coordinates, then we can get the coordinates of the whole vector.

Let's say we have a vector whose beginning and end have the following designations and coordinates: A(A x ; Ay) and B(B x ; By)

To obtain the coordinates of a given vector, it is necessary to subtract the corresponding coordinates of the beginning from the coordinates of the end of the vector:

To determine the coordinates of a vector in space, use the following formula:

Dot product of vectors

There are two ways to define the concept of a scalar product:

Geometric method. According to it, the scalar product is equal to the product of the values of these modules and the cosine of the angle between them.

Algebraic meaning. From the point of view of algebra, the scalar product of two vectors is a certain quantity that is obtained as a result of the sum of the products of the corresponding vectors.

If the vectors are given in space, then you should use a similar formula:

Properties:

If you multiply two identical vectors scalarly, then their scalar product will not be negative:

If the scalar product of two identical vectors turns out to be equal to zero, then these vectors are considered zero:

If a certain vector is multiplied by itself, then the scalar product will be equal to the square of its modulus:

The scalar product has a communicative property, that is, if the vectors are rearranged, the scalar product will not change:

The scalar product of non-zero vectors can be equal to zero only if the vectors are perpendicular to each other:

For a scalar product of vectors, the commutative law is valid in the case of multiplying one of the vectors by a number:

With a scalar product, you can also use the distributive property of multiplication:

Angle between vectors