Geometry as a separate subject begins for schoolchildren in the 7th grade. Until that time they touch geometric problems a fairly light form and basically what can be seen using visual examples: the area of a room, a plot of land, the length and height of walls in rooms, flat objects, etc. At the beginning of studying geometry itself, the first difficulties appear, such as, for example, the concept of a straight line, since it is not possible to touch this straight line with your hands. As for triangles, this is the simplest type of polygon, containing only three angles and three sides.
Classmates
The theme of triangles is one of the main ones important and big topics school curriculum in geometry 7-9 grades. Having mastered it well, it is possible to decide very complex tasks. In this case, you can initially consider a completely different geometric figure, and then divide it for convenience into suitable triangular parts.
To work on the proof of equality ∆ ABC And ∆A1B1C1 You need to thoroughly understand the signs of equality of figures and be able to use them. Before studying the signs, you need to learn determine equality sides and angles of the simplest polygons.
To prove that the angles of triangles are equal, the following options will help:
- ∠ α = ∠ β based on the construction of the figures.
- Given in the task conditions.
- With two parallel lines and the presence of a secant, both internal cross-lying and corresponding ones can be formed ∠ α = ∠ β.
- Adding (subtracting) to (from) ∠ α = ∠ β equal angles.
- Vertical ∠ α and ∠ β are always similar
- General ∠ α, simultaneously belonging to ∆MNK And ∆MNH .
- The bisector divides ∠ α into two equal ones.
- Adjacent to ∠ 90°- angle equal to the original one.
- Adjacent equal angles are equal.
- The height forms two adjacent ∠ 90° .
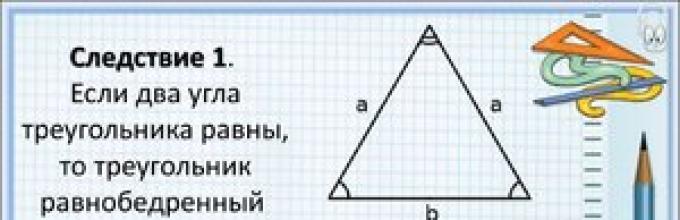
- In isosceles ∆MNK at the base ∠ α = ∠ β.
- Equal ∆MNK And ∆SDH corresponding ∠ α = ∠ β.
- Previously proven equality ∆MNK And ∆SDH .
This is interesting: How to find the perimeter of a triangle.
3 signs that triangles are equal
Proof of equality ∆ ABC And ∆A1B1C1 very convenient to produce, based on basic signs the identity of these simplest polygons. There are three such signs. They are very important in solving many geometric problems. Each one is worth considering.
The characteristics listed above are theorems and are proven by the method of superimposing one figure on another, connecting vertices corresponding angles and the beginning of the rays. Proofs for the equality of triangles in grade 7 are described in a very accessible form, but are difficult for schoolchildren to study in practice, since they contain large number elements designated by capital Latin letters. This is not entirely familiar to many students when they start studying the subject. Teenagers get confused about the names of sides, rays, and angles.
A little later another one appears important topic"Similarity of triangles." The very definition of “similarity” in geometry means similarity of shape with different sizes. For example, you can take two squares, the first with a side of 4 cm, and the second 10 cm. These types of quadrangles will be similar and, at the same time, have a difference, since the second will be larger, and each side will be increased by the same number of times.
In considering the topic of similarity, 3 signs are also given:
- The first is about the two correspondingly equal angles of the two triangular figures in question.
- The second is about the angle and the sides that form it ∆MNK, which are equal to the corresponding elements ∆SDH .
- The third one indicates the proportionality of all corresponding sides of the two desired figures.
How can you prove that the triangles are similar? It is enough to use one of the above signs and correctly describe the entire process of proving the task. Theme of similarity ∆MNK And ∆SDH is easier to perceive by schoolchildren based on the fact that by the time of studying it, students are already fluent in using the notation of elements in geometric constructions, do not get confused by a huge number of names and know how to read drawings.
Concluding the passage of the extensive topic of triangular geometric shapes, students should already know perfectly how to prove equality ∆MNK = ∆SDH on two sides, set the two triangles to be equal or not. Considering that a polygon with exactly three angles is one of the most important geometric figures, mastering the material should be taken seriously, paying special attention to even minor facts of the theory.
Two triangles are said to be congruent if they can be brought together by overlapping. Figure 1 shows equal triangles ABC and A 1 B 1 C 1 . Each of these triangles can be superimposed on the other so that they are completely compatible, that is, their vertices and sides are compatible in pairs. It is clear that the angles of these triangles will also match in pairs.
Thus, if two triangles are congruent, then the elements (i.e. sides and angles) of one triangle are respectively equal to the elements of the other triangle. Note that in equal triangles against correspondingly equal sides(i.e., overlapping when superimposed) equal angles lie and back: Equal sides lie opposite respectively equal angles.
So, for example, in equal triangles ABC and A 1 B 1 C 1, shown in Figure 1, opposite equal sides AB and A 1 B 1, respectively, lie equal angles C and C 1. We will denote the equality of triangles ABC and A 1 B 1 C 1 as follows: Δ ABC = Δ A 1 B 1 C 1. It turns out that the equality of two triangles can be established by comparing some of their elements.
Theorem 1. The first sign of equality of triangles. If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent (Fig. 2).
Proof. Consider triangles ABC and A 1 B 1 C 1, in which AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (see Fig. 2). Let us prove that Δ ABC = Δ A 1 B 1 C 1 .
Since ∠ A = ∠ A 1, then triangle ABC can be superimposed on triangle A 1 B 1 C 1 so that vertex A is aligned with vertex A 1, and sides AB and AC are respectively superimposed on rays A 1 B 1 and A 1 C 1. Since AB = A 1 B 1, AC = A 1 C 1, then side AB will align with side A 1 B 1 and side AC will align with side A 1 C 1; in particular, points B and B 1, C and C 1 will coincide. Consequently, sides BC and B 1 C 1 will align. So, triangles ABC and A 1 B 1 C 1 are completely compatible, which means they are equal.
Theorem 2 is proved similarly by the superposition method.
Theorem 2. The second sign of equality of triangles. If a side and two adjacent angles of one triangle are respectively equal to the side and two adjacent angles of another triangle, then such triangles are congruent (Fig. 34).
Comment. Based on Theorem 2, Theorem 3 is established.
Theorem 3. The sum of any two interior angles of a triangle is less than 180°.
Theorem 4 follows from the last theorem.
Theorem 4. An exterior angle of a triangle is greater than any interior angle not adjacent to it.
Theorem 5. The third sign of equality of triangles. If three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent ().
Example 1. In triangles ABC and DEF (Fig. 4)
∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm. Compare triangles ABC and DEF. What angle in triangle DEF is equal to angle B?
Solution. These triangles are equal according to the first sign. Angle F of triangle DEF is equal to angle B of triangle ABC, since these angles lie opposite respectively equal sides DE and AC.
Example 2. Segments AB and CD (Fig. 5) intersect at point O, which is the middle of each of them. What is the length of segment BD if segment AC is 6 m?
Solution.
Triangles AOC and BOD are equal (according to the first criterion): ∠ AOC = ∠ BOD (vertical), AO = OB, CO = OD (by condition).
From the equality of these triangles it follows that their sides are equal, i.e. AC = BD. But since according to the condition AC = 6 m, then BD = 6 m.
From ancient times to this day, the search for signs of equality of figures is considered basic task, which is the basis of the fundamentals of geometry; hundreds of theorems are proven using equality tests. The ability to prove equality and similarity of figures is an important task in all areas of construction.
Putting the skill into practice
Suppose we have a figure drawn on a piece of paper. At the same time, we have a ruler and a protractor with which we can measure the lengths of segments and the angles between them. How to transfer a figure of the same size to a second sheet of paper or double its scale.
We know that a triangle is a figure made up of three segments called sides that form the angles. Thus, there are six parameters - three sides and three angles - that define this figure.
However, having measured the size of all three sides and angles, transferring this figure to another surface will be a difficult task. In addition, it makes sense to ask the question: wouldn’t it be enough to know the parameters of two sides and one angle, or just three sides?
Having measured the length of the two sides and between them, we will then put this angle on a new piece of paper, so we can completely recreate the triangle. Let's figure out how to do this, learn how to prove the signs by which they can be considered the same, and decide what minimum number of parameters is enough to know in order to be confident that the triangles are the same.
Important! Figures are called identical if the segments forming their sides and angles are equal to each other. Similar figures are those whose sides and angles are proportional. Thus, equality is similarity with a proportionality coefficient of 1.
What are the signs of equality of triangles? Let’s give their definition:
- the first sign of equality: two triangles can be considered identical if two of their sides are equal, as well as the angle between them.
- the second sign of equality of triangles: two triangles will be the same if two angles are the same, as well as the corresponding side between them.
- third sign of equality of triangles : Triangles can be considered identical when all their sides are of equal length.
How to prove that triangles are congruent. Let us give a proof of the equality of triangles.
Evidence of 1 sign
For a long time, among the first mathematicians this sign was considered an axiom, however, as it turned out, it can be proven geometrically based on more basic axioms.
Consider two triangles - KMN and K 1 M 1 N 1 . The KM side has the same length as K 1 M 1, and KN = K 1 N 1. And the angle MKN is equal to the angles KMN and M 1 K 1 N 1.
If we consider KM and K 1 M 1, KN and K 1 N 1 as two rays that come out from the same point, then we can say that the angles between these pairs of rays are the same (this is specified by the condition of the theorem). Let us carry out a parallel transfer of rays K 1 M 1 and K 1 N 1 from point K 1 to point K. As a result of this transfer, rays K 1 M 1 and K 1 N 1 will completely coincide. Let us plot on the ray K 1 M 1 a segment of length KM, originating at point K. Since, by condition, the resulting segment will be equal to the segment K 1 M 1, then the points M and M 1 coincide. Similarly with the segments KN and K 1 N 1. Thus, by transferring K 1 M 1 N 1 so that the points K 1 and K coincide, and the two sides overlap, we obtain a complete coincidence of the figures themselves.
Important! On the Internet there are proofs of the equality of triangles based on two sides and an angle using algebraic and trigonometric identities with numerical values of sides and angles. However, historically and mathematically this theorem was formulated long before algebra and earlier than trigonometry. To prove this feature of the theorem, it is incorrect to use anything other than the basic axioms.
Evidence 2 signs
Let us prove the second sign of equality in two angles and a side, based on the first.
Evidence 2 signs
Let's consider KMN and PRS. K is equal to P, N is equal to S. Side KN has the same length as PS. It is necessary to prove that KMN and PRS are the same.
Let us reflect the point M relative to the ray KN. Let's call the resulting point L. In this case, the length of the side KM = KL. NKL is equal to PRS. KNL is equal to RSP.
Since the sum of the angles is equal to 180 degrees, then KLN is equal to PRS, which means PRS and KLN are the same (similar) on both sides and the angle, according to the first sign.
But, since KNL is equal to KMN, then KMN and PRS are two identical figures.
Evidence 3 signs
How to determine that triangles are congruent. This follows directly from the proof of the second feature.
Length KN = PS. Since K = P, N = S, KL=KM, and KN = KS, MN=ML, then:
This means that both figures are similar to each other. But since their sides are the same, they are also equal.
Many consequences follow from the signs of equality and similarity. One of them is that in order to determine whether two triangles are equal or not, it is necessary to know their properties, whether they are the same:
- all three sides;
- both sides and the angle between them;
- both angles and the side between them.
Using the triangle equality test to solve problems
Consequences of the first sign
In the course of the proof, one can come to a number of interesting and useful consequences.
- . The fact that the point of intersection of the diagonals of a parallelogram divides them into two identical parts is a consequence of the signs of equality and is quite amenable to proof. The sides of the additional triangle (with a mirror construction, as in the proofs that we performed) are the sides of the main one (the sides of the parallelogram).
- If there are two right triangles that have the same sharp corners, then they are similar. If the leg of the first is equal to the leg of the second, then they are equal. This is quite easy to understand - all right triangles have a right angle. Therefore, the signs of equality are simpler for them.
- Two triangles with right angles, in which two legs have the same length, can be considered identical. This is due to the fact that the angle between the two legs is always 90 degrees. Therefore, according to the first criterion (by two sides and the angle between them), all triangles with right angles and identical legs are equal.
- If there are two right triangles, and their one leg and hypotenuse are equal, then the triangles are the same.
Let's prove this simple theorem.
There are two right triangles. One has sides a, b, c, where c is the hypotenuse; a, b - legs. The second has sides n, m, l, where l is the hypotenuse; m, n - legs.
According to the Pythagorean theorem, one of the legs is equal to:
;
.
Thus, if n = a, l = c (equality of legs and hypotenuses), respectively, the second legs will be equal. The figures, accordingly, will be equal according to the third characteristic (on three sides).
Let us note one more important consequence. If there are two equal triangles, and they are similar with a similarity coefficient k, that is, the pairwise ratios of all their sides are equal to k, then the ratio of their areas is equal to k2.
The first sign of equality of triangles. Video lesson on geometry 7th grade
Geometry 7 The first sign of equality of triangles
Conclusion
The topic we have discussed will help any student better understand the basic geometric concepts and improve your skills in most interesting world mathematics.
From school course In geometry, the sign of equality of triangles along two sides and the angle between them is well known, namely:
If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent (Fig. 1).
It is natural to raise the question of whether triangles will be congruent if the corresponding equal angles in the triangles are not contained between equal sides. Is it true that if two sides and an angle of one triangle are respectively equal to two sides and an angle of another triangle, then such triangles are congruent.
It turns out this is not true. Let's give an example. Consider a circle and its chord AB (Fig. 2). With the center at point A, we draw another circle intersecting the first circle at some points C and C 1. Then in triangles ABC and ABC 1 AB is a common side, AC = AC 1,C = Since 1, however triangles ABC and ABC 1 are not congruent.
In the formulation of signs of equality of triangles, you can include not only sides and angles, but also other elements of triangles. Let's consider several formulations of criteria for the equality of triangles by three elements, including sides, angles, altitudes, bisectors and medians of triangles. Let us find out the validity of the corresponding signs.
If the angle, the side opposite this angle, and the height dropped to the other side of one triangle are respectively equal to the angle, side and height of another triangle, then such triangles are congruent.
Let in triangles ABC And A 1 B 1 C 1 WITH = WITH 1 , AB = A 1 B 1, height A.H. equal to height A 1 H 1 (Fig. 3). Let us prove that triangles ABC And A 1 B 1 C 1 are equal.
Right Triangles ABH And A 1 B 1 H 1 are equal in leg and hypotenuse. Means, B = B 1. Considering that WITH = WITH 1, we have equality A = A 1. Thus, in triangles ABC And A 1 B 1 C 1
AB= A 1 B 1 , A = A 1 , B = B 1 .
Therefore, these triangles are equal in side and two adjacent angles.
Let the angle, the side adjacent to this angle, and the height lowered to the other side adjacent to the given angle of one triangle be respectively equal to the angle, side and height of the other triangle (Fig. 4).
Let us give an example showing that the equality of the indicated elements of the triangles is not sufficient for the equality of the triangles themselves.
Let's consider right triangles ABH And A 1 B 1 H 1 (H = H 1 = 90 o), in which
AB = A 1 B 1 , B = B 1 , A.H. = A 1 H 1
(Fig. 5). On the continuations of the sides B.H. And B 1 H 1 set aside unequal segments HC And H 1 C 1. Then in triangles ABC And A 1 B 1 C 1
AB = A 1 B 1 , B = B 1 ,
heights A.H. And A 1 H 1 are equal, but the triangles themselves are not equal.
If two sides and the median enclosed between them of one triangle are respectively equal to two sides and the median of another triangle, then such triangles are congruent.
Let in triangles ABC And A 1 B 1 C 1
A.C.= A 1 C 1 , B.C. = B 1 C 1 ,
median SM equal to median C 1 M 1 (Fig. 6). Let us prove that triangles ABC And A 1 B 1 C 1 are equal.
Let's continue the medians and set aside the segments M.D. = C.M. And M 1 D 1 = C 1 M 1 (Fig. 6).
Quadrilaterals ACBD And A 1 WITH 1 B 1 D 1 - parallelograms. Triangles ACD And A 1 C 1 D
ACD = A 1 C 1 D 1 .
Likewise, triangles BCD And B 1 C 1 D 1 are equal on three sides. Hence,
BCD = B 1 C 1 D 1 .
Means, WITH = WITH 1 and triangles ABC And A 1 B 1 C 1 are equal on both sides and the angle between them.
Let the angle, the side adjacent to this angle, and the median drawn to this side of one triangle be respectively equal to the angle, side and median of another triangle (Fig. 7).
Consider a circle with center at point M(Fig. 8). Let's draw two diameters AB And A 1 B 1. Through dots A, A 1 , M draw another circle and select a point on it C as shown in the picture. In triangles ABC And A 1 B 1 C
AB = A 1 B 1 , A = A 1 ,
median C M ABC And A 1 B 1 C not equal.
If a side and two medians drawn to two other sides of one triangle are respectively equal to a side and two medians of another triangle, then such triangles are congruent.
Let in triangles ABC And A 1 B 1 C 1 AB = A 1 B 1, median A.M. equal to the median A 1 M 1, median B.K. equal to the median B 1 K 1 (Fig. 9). Let us prove that triangles ABC And A 1 B 1 C 1 are equal.
Points O And O 1, the intersections of the medians of these triangles divide the medians in a ratio of 2:1, counting from the vertex. So triangles ABO And A 1 B 1 O 1 are equal on three sides. Hence,
BAO = B 1 A 1 O 1 ,
that means triangles A.B.M. And A 1 B 1 M 1 are equal on both sides and the angle between them. That's why
ABC = A 1 B 1 C 1 .
Similarly, it is proved that
BAC = B 1 A 1 C 1 .
So the triangles ABC And A 1 B 1 C 1 are equal in side and two adjacent angles.
Let the angle and two medians drawn to its sides of one triangle be respectively equal to the angle and two medians of another triangle (Fig. 10).
Let us give an example showing that the equality of the indicated elements is not enough for the equality of the triangles themselves.
To do this, consider two equal circles with centers at points O 1 and O 2 touching each other at a point M(Fig. 11).
Let's draw a chord in one of them AB and direct A.M., intersecting the second circle at some point C. Let's draw a segment B.C.. We get a triangle ABC. Let's draw a median in it CK and denote O a point dividing it in a ratio of 2:1, counting from the vertex C. Let's draw a circle with the center at the point O, radius O.C., intersecting the second circle at the point C 1. Let's make a direct C 1 M and denote A 1 its point of intersection with the first circle. Let's denote K 1 chord intersection point A 1 B and straight C 1 O. In triangles ABC And A 1 B.C. 1 A = A 1, median CK And C 1 K 1 equal, median B.M.- general. However, triangles ABC And A 1 B.C. 1 are not equal.
If two sides and the bisector between them of one triangle are respectively equal to two sides and the bisector of another triangle, then such triangles are congruent.
Let in triangles ABC And A 1 B 1 C 1
A.C.= A 1 C 1 , B.C. = B 1 C 1 ,
bisector CD equal to the bisector WITH 1 D 1. Let us prove that triangles ABC And A 1 B 1 C 1 are equal.
Let's continue the sides A.C. And A 1 C 1 and plot the segments on their continuations C.E. = B.C. And C 1 E 1
= B 1 C 1 (Fig. 12). Then 
Triangles B.C.E. And B 1 C 1 E 1 are equal on three sides. Means, E = E 1 and BE = B 1 E 1. Triangles ABE And A 1 B 1 E 1 are equal on both sides and the angle between them. Means, AB = A 1 B 1. So the triangles ABC And A 1 B 1 C 1 are equal on three sides.
Let the angle, the side adjacent to this angle, and the bisector drawn to the other side adjacent to the given angle of one triangle be respectively equal to the angle, side and bisector of another triangle (Fig. 13).
Example of triangles ABC And ABC 1, shown in Figure 14, shows that the equality of the indicated elements is not enough for the equality of the triangles themselves.
Indeed, in triangles ABC And ABC 1 B- general, AB- common side, bisectors AD And AD 1 are equal. However, triangles ABC And ABC 1 are not equal.
Let the side, median and height drawn to the other two sides of one triangle be respectively equal to the side, median and height of the other triangle (Fig. 15).
Let us give an example showing that the equality of the indicated elements is not enough for the equality of the triangles themselves.
To do this, consider a circle and an angle with a vertex in the center A this circle (Fig. 16). Let's put a segment on its side AB, larger in diameter, and through its middle K draw a straight line parallel to the other side of the angle and intersecting the circle at some points M And M 1. Let's draw straight lines B.M., B.M. 1 and the points of their intersection with the side of the angle we denote accordingly C And C 1. Then in triangles ABC And ABC 1 side AB- total, height B.H.- total, median A.M. And A.M. 1 are equal, but the triangles ABC And ABC 1 are not equal.
Two triangles are congruent if the side, median, and altitude drawn to the other side of one triangle are respectively equal to the side, median, and altitude of the other triangle.
Let in triangles ABC And A 1 B 1 C 1 A.C. = A 1 C 1, median C.M. And C 1 M 1 equal, heights CH And C 1 H 1 are equal (Fig. 17). Let us prove that triangles ABC And A 1 B 1 C 1 are equal.Indeed, right triangles ACH And A 1 C 1 H 1 are equal in hypotenuse and leg. Therefore F A=F A 1 and A.H. = A 1 H 1. Right Triangles CMH And C 1 M 1 H 1 are equal in hypotenuse and leg. Hence, M.H. = M 1 H 1, from where A.M. = A 1 M 1 means AB = A 1 B 1. So the triangles ABC And A 1 B 1 C 1 are equal on both sides and the angle between them.
Two triangles are equal if the three medians of one triangle are respectively equal to the three medians of the other triangle.
Let in triangles ABC And A 1 B 1 C 1 are respectively equal to the median A.K. And A 1 K 1 , B.L. And B 1 L 1 , C.M. And C 1 M 1 (Fig. 18). Let us prove that triangles ABC And A 1 B 1 C 1 are equal.
Let O And O 1 - intersection points of the medians of these triangles. Note that the medians OM And O 1 M 1 triangles ABO And A 1 B 1 O 1 are equal, since they constitute one third of the corresponding medians of these triangles.
According to the criterion of equality of triangles, which we proved under number 3, triangles ABO And A 1 B 1 O 1 are equal, which means AB = A 1 B 1 .
Similarly, it is proved that B.C. = B 1 C 1 and A.C. = A 1 C 1. So the triangles ABC And A 1 B 1 C 1 are equal on three sides.
Two triangles are equal if the three heights of one triangle are respectively equal to the three heights of the other triangle.
Let in triangles ABC And A 1 B 1 C 1 are respectively equal to the heights A.H. And A 1 H 1 , B.G. And B 1 G 1 , CF And C 1 F 1 (Fig. 19). Let us prove that triangles ABC And A 1 B 1 C 1 are equal.
Let us denote the sides of the triangles respectively a, b, c And a 1 , b 1 , c 1, and the corresponding heights h a, b b, h c And h 1a , h 1b , h 1c. There are equalities ah a = bh b = ch c And a 1 h 1a = b 1 h 1b = c 1 h 1c. Dividing the first equalities term by term into the second, we obtain equalities from which it follows that triangles ABC And A 1 B 1 C 1 are similar. Since the corresponding heights of these triangles are equal, they are not only similar, but also equal.
